E-mail Alert Rss
 

物探与化探, 2022, 46(4): 925-933 doi: 10.11720/wtyht.2022.1572

方法研究·信息处理·仪器研制

基于LSTM循环神经网络的大地电磁方波噪声抑制

杨凯,1,2, 唐卫东1, 刘诚1, 贺景龙1, 姚川1

1.中国地质调查局 西安矿产资源调查中心,陕西 西安 710000

2.中国地质大学(武汉) 地球物理与空间信息学院,湖北 武汉 430074

Suppression of magnetotelluric square wave noise based on a LSTM recurrent neural network

YANG Kai,1,2, TANG Wei-Dong1, LIU Cheng1, HE Jing-Long1, YAO Chuan1

1. Xi'an Center of Mineral Resources Survey, China Geological Survey, Xi'an 710000, China

2. Institute of Geophysics & Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China

责任编辑: 沈效群

收稿日期: 2021-10-25   修回日期: 2022-02-8  

基金资助: 中国地质调查局地质调查项目“北山地区月牙山—合黎山一带萤石铜钼矿调查评价”(DD20211552)
“秦岭地区金银矿资源勘查”(DD20208008)
“陕西旬阳—镇坪地区铅锌矿产地质调查”(DD20208009)

Received: 2021-10-25   Revised: 2022-02-8  

作者简介 About authors

杨凯(1991-),男,在读硕士,工程师,主要从事物探数据处理工作。Email: yangkaicgs@163.com

摘要

去噪是大地电磁数据处理的重要一环。为了丰富和发展大地电磁时间序列去噪方法,将循环神经网络中的LSTM网络引入大地电磁时间序列方波噪声处理中,将实测无人文干扰的大地电磁时间序列叠加模拟方波噪声作为网络输入,将无噪原始时间序列作为网络的目标输出,训练了1 500次epoch后,网络从仿真含噪信号提取的时间序列与原始时间序列的归一化互相关系数高达0.971 8,说明网络很好地学习了无噪大地电磁时间序列的特征。通过实测含方波噪声信号的去噪试验,表明了本文方法可以有效压制方波噪声干扰,改善阻抗估计质量,为深度学习在大地电磁时间序列处理的应用提供了新思路。

关键词： 大地电磁; 时间序列; LSTM; 深度学习; 去噪

Abstract

Denoising is an important part of magnetotelluric data processing. To enrich and develop the denoising method of magnetotelluric time series, this study introduced the LSTM network-one of the recurrent neural networks-into the square wave noise processing of the magnetotelluric time series. Different from previous studies, the measured magnetotelluric time series without human interference superimposed on simulated square wave noise were used as the input of the LSTM network, and the noise-free original time series were used as the target output of the network. After training for 1,500 epochs, the normalized cross-correlation coefficient between the time series extracted from the simulated noise signals by the network and the original time series reached 0.9718, indicating that the network has effectively learned the characteristics of the noise-free magnetotelluric time series. Finally, the denoising test results of measured square wave noise signals show that the proposed method can effectively suppress the interference of square wave noise and improve the estimation quality of impedance. This study provides a new idea for the processing of magnetotelluric time series based on deep learning.

Keywords： magnetotellurics; time series; LSTM; deep learning; denoising

PDF (5389KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

杨凯, 唐卫东, 刘诚, 贺景龙, 姚川. 基于LSTM循环神经网络的大地电磁方波噪声抑制[J]. 物探与化探, 2022, 46(4): 925-933 doi:10.11720/wtyht.2022.1572

YANG Kai, TANG Wei-Dong, LIU Cheng, HE Jing-Long, YAO Chuan. Suppression of magnetotelluric square wave noise based on a LSTM recurrent neural network[J]. Geophysical and Geochemical Exploration, 2022, 46(4): 925-933 doi:10.11720/wtyht.2022.1572

0 引言

大地电磁测深是一种以天然电磁场为场源的地球物理勘探方法,其观测频带较宽,有效信号微弱,随着人文噪声的日益增加,大地电磁的“净土”已经基本消失。其中,由测区附近用电设备的充放电所引起的方波噪声是一种常见的高强度噪声,主要集中在电道,可产生高于正常信号十几倍到几十倍的干扰[1-2],这类噪声影响幅度大,影响频点多,极大干扰了阻抗估计的结果。为了压制方波干扰,许多学者做了大量研究:严家斌[3]提出了基于小波变换的迭代回归噪声改正方法,对含方波干扰的脉冲类噪声进行了压制,有效改善了数据质量;蔡建华等[4]将经验模态分解(EMD)应用于方波噪声处理,突出了有用信号;汤井田、李晋等[5]提出了一种基于数学形态滤波的大地电磁去噪方法,对安徽庐枞矿集区的方波、脉冲、三角波等噪声进行了处理,有效抑制了大尺度干扰和基线漂移;汤井田、刘祥等[6]讨论了不同仿真方波噪声对测深曲线的影响及远参考法对其的去噪效果,研究表明远参考在一定条件下可以消除方波干扰;王辉、魏文博等[7]利用同步大地电磁时间序列信号之间的关系,用合成的无噪数据段代替含噪数据段,成功去除了大于窗口长度的方波噪声,精度较高,但该方法需要一段无明显干扰的远参考数据;汤井田、李广等[8]通过字典学习提取人文干扰特征,利用构建的冗余字典分离了AMT数据中的仿真方波噪声;李晋、张贤等[9]利用变分模态分解(VMD)和匹配追踪(MP)对模拟方波噪声进行了处理,明显改善了数据质量。

近年来,深度学习已经在地球物理部分方法的应用中取得了不错的效果[10],不少学者将其成功引入电磁、地震数据处理以及重磁反演等地球物理领域[11-15]。深度学习方法适用范围广,泛化能力强,在大地电磁方面的应用主要集中在时间序列处理上,Manoj和Nagarajan[16]最早提出了利用人工神经网络自动执行大地电磁时间序列编辑的方法,该方法提高了工作效率减少了人工编辑的主观因素。本文所应用的长短时记忆网络(long short-term memory, LSTM)是一种特殊的循环神经网络,该神经网络在语音识别、自然语言处理以及时间序列相关的领域有较为广泛的应用,近年来也被逐渐引入到地球物理领域,例如:许滔滔等[17]将LSTM网络应用于工频干扰压制,有效去除了工频干扰;王斯昊等[18]用LSTM网络去除了时间序列的阶跃信号;汪凯翔等[19]利用LSTM网络对地电场数据进行了处理,去除了测试集中不同种类的噪声。以上方法都是以时间序列的低频、大尺度噪声或者信号轮廓为网络输出值。与前人不同的是,本文使用大地电磁信号本身作为网络输出,通过选取标准大地电磁时间序列随机添加仿真方波噪声作为网络训练输入,以无噪大地电磁时间序列作为网络目标输出,让网络存储和学习大地电磁信号本身的特征,从含噪时间序列中自动提取符合大地电磁信号特征的序列,从而实现抑制方波噪声的目的。

1 LSTM网络简介

长短时记忆网络(LSTM)是一种特殊的循环神经网络,由Hochreiter和Schmidhuber于1997年提出[20],主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题,被广泛应用于时间序列相关领域。

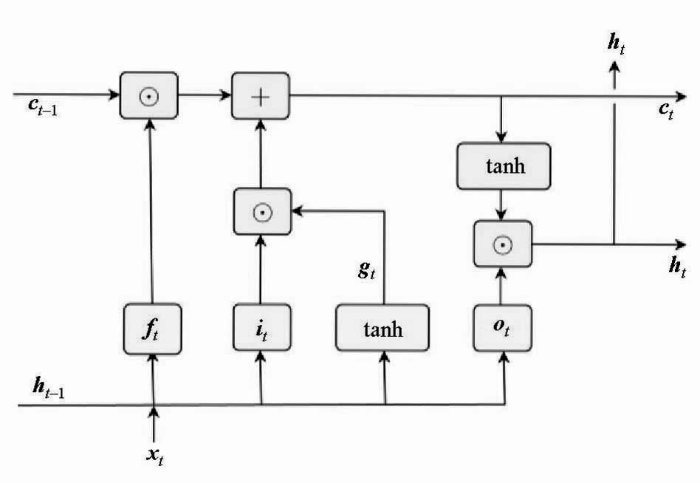
一个标准的LSTM网络神经元包含了3个门(输入门、输出门、遗忘门)和1个记忆细胞(图1),可以归纳为以下几式:

ft=σ(Wf·[ht-1,xt]+bf),
it=σ(Wi·[ht-1,xt]+bi),
ot=σ(Wo·[ht-1,xt]+bo)
gt=tanh(Wg·[ht-1,xt]+bg),
ct=gt☉it+ct-1☉ft,
ht=tanh(ct)☉ot,

式中:ht-1为t-1时刻即上一个神经元的隐藏层;xt为t时刻的特征向量;σ为sigmoid激活函数;it、ft、ot分别为t时刻输入门、遗忘门和输出门的状态;gt为t时刻记忆细胞的候选值;ct为t时刻记忆细胞的状态,也作为t+1时刻即下一个神经元的初始记忆细胞;ht为t时刻的隐藏层,也为t+1时刻即下一个神经元的初始隐藏层;Wi、Wf、Wo、Wg为传播权重矩阵;bi、bf、bo、bg为偏置向量;☉表示矩阵元素对应相乘。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   LSTM网络神经元基本结构

Fig.1   Basic structure of LSTM


总的来说,单向LSTM神经元内部有3个处理步骤:

第一步为选择忘记阶段,主要是对上一个节点传进来的输入进行选择性忘记。根据上一个神经元所传递的隐藏层ht-1和本神经元的输入xt生成遗忘门ft,来控制上一个神经元所传递的记忆细胞ct-1中哪些需要留,哪些需要“忘”(式(1)、式(5))。

第二步为选择记忆阶段,主要是通过上一个神经元的隐藏层和本次的输入xt生成输入门it,再与t时刻记忆细胞的候选值gt作用来决定需要记住的信息(式(2)、式(4)、式(5))。

第三部为输出阶段。通过前两个阶段的“遗忘”和“记忆”,共同决定了记忆细胞ct的最新状态,而后ct通过激活函数tanh的放缩,由输出门ot控制生成新的隐藏层状态ht(式(4)、式(5)、式(6))。

本文使用双向LSTM网络。双向LSTM网络就是在序列正向处理的基础上将序列逆向再处理一次,这样神经元不仅能获取“过去”时刻的序列信息,也能获取“未来”时刻的信息,能更好地记录其上下文的关系,从而取得更佳的学习效果。

2 LSTM网络搭建

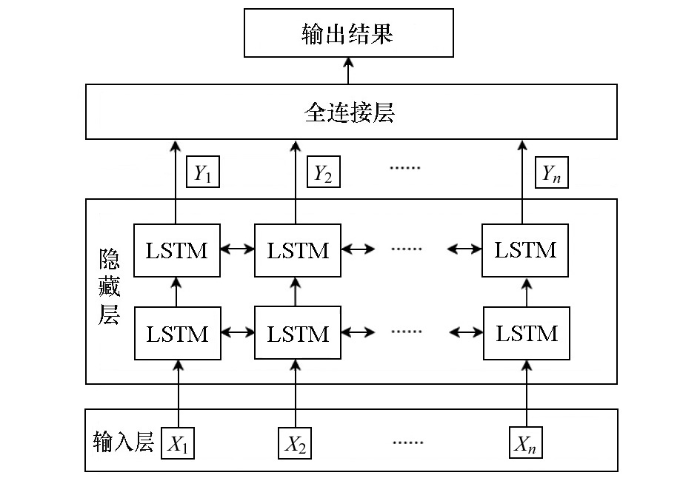
2.1 网络设计

本网络主要由输入层、隐藏层和全连接层构成,通过实际测试和查阅文献将隐藏层层数设置为2,每层128个节点,全连接层输出维度设为1(如图2所示),损失函数使用均方误差损失函数(MSEloss),优化器使用适应性矩估计优化器(adaptive moment estimation,Adam),该优化器具有收敛速度快、调参方便等优点,适合解决含大规模数据和参数的优化问题[21]。需要注意的是,网络结构的设计和参数的选择带有一定的经验性和主观性,需要在参考前人结果的基础上不断调整试验,针对需要解决的问题选择最合适的组合。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   LSTM网络结构示意

Fig.2   LSTM network structure


2.2 网络训练

网络训练主要包括数据集构建、数据集归一化(或标准化)、网络训练和验证等几个步骤。

2.2.1 数据集构建

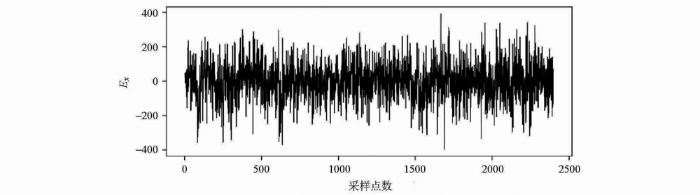
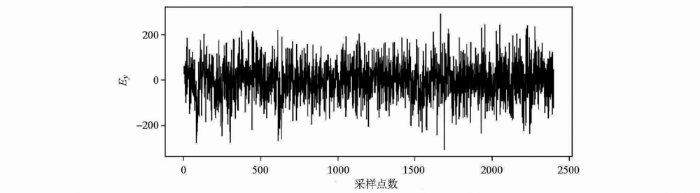
选取2020年10月12日在陕西省宁强县某地用MTU-5A大地电磁仪采集的、无明显人文干扰且阻抗估计稳定的数据段Ex通道序列,将其视为无噪声的大地电磁时间序列,长度2 400个点,采样率2 400 Hz(图3)。首先,随机生成100组方波信号,因为待处理的实测方波噪声主频在24 Hz左右,故模拟方波噪声频率随机分布在23~25 Hz之间,振幅在该段无噪时间序列最大值与最小值之差的0.1~8倍之间随机取值,相位随机。而后,将所有模拟方波噪声各自叠加在无噪大地电磁时间序列上,合成100组仿真含噪信号,并在每组仿真信号中随机截取64组长度 1 200个点的信号,共产生6 400组信号作为训练集;选取与训练集Ex对应的Ey通道数据,长度2 400个点,采样率2 400 Hz(图4),将该段数据采用与合成训练集同样的方式生成20组仿真含方波噪声时间序列,而后每组信号随机截取64组长度为1 200个点的信号,共1 280组信号作为验证集,以验证网络的实际处理能力。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   训练集原始时间序列

Fig.3   Original time series of training set


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   验证集原始时间序列

Fig.4   Original time series of validation set


2.2.2 数据归一化

数据集构建好后还要进行数据归一化(或标准化),归一化后数据可以提高网络的收敛速度和网络精度,根据大地电磁时间序列数据的特征,将其归一化至1~-1之间。

对于网络输入数据:

xnorm=(x-xmean)/xmax,

式中:x为添加模拟噪声的大地电磁时间序列数据,xmean为其平均值,xmax为其最大值,xnorm为归一化值。

对于网络的目标输出数据:

ynorm=y/xmax,

式中:y为不含噪声的大地电磁时间序列数据,xmax为含噪数据的最大值,ynorm为归一化值。

对所有输入网络的数据都要进行归一化,包括训练集、验证集,由于网络的理想输出为归一化值,输出后还要进行反归一化:

ypred=xmaxynorm_pred,

式中:ypred为反归一化值,即为实际无噪大地电磁数据;ynorm_pred为网络输出的归一化预测值;xmax为网络输入的含噪大地电磁信号的最大值。

2.2.3 网络的训练和验证

将bitch_size(一次训练所选取的样本数)设为32,epoch(使用训练集中的全部样本训练一次即为1个epoch)数设置为3 000,以保证网络的收敛。

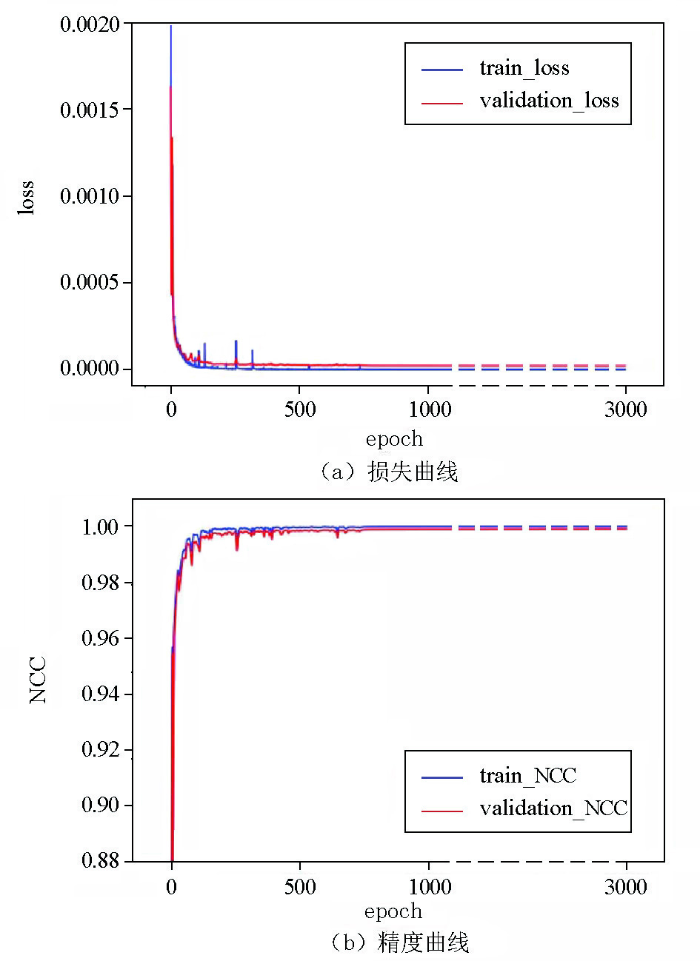
评价网络训练效果的主要有网络损失曲线和网络精度曲线。本文选取网络理想输出时间序列和实际输出时间序列的归一化互相关系数(normalized cross correlation,NCC)作为检验网络精度的参数,具体计算如下:

NCC=∑n=1Nf(n)g(n)∑n=1Nf2(n)·∑n=1Ng2(n),

式中:N表示数据长度;f(n) 和g(n)为2组离散序列;NCC值在-1~1之间,-1代表2组序列相位相反,0代表2组序列正交,1代表2组序列完全相同,NCC越接近于1说明2组序列相似性越高。

由LSTM网络的学习曲线(图5)可知,前500次epoch损失曲线急剧下降,精度曲线快速上升;训练500次以后损失曲线缓慢下降,精度曲线缓慢上升,训练集损失(train_loss)略小于验证集(validation_loss),训练集精度(train_NCC)略大于验证集(validation_NCC)。当训练至1 500次epoch时,训练集的平均NCC可达0.999 98,验证集的平均NCC可达0.999 03,说明网络很好地从含方波噪声的序列中提取出了有效大地电磁时间序列。训练1 500次以后网络趋于稳定,验证集损失几乎不再减小,精度不再明显增加,故取epoch为1 500的网络为最终模型,用来进行下一步去噪测试。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   LSTM网络学习曲线

Fig.5   LSTM network learning curve


3 去噪测试

3.1 仿真含噪信号去噪

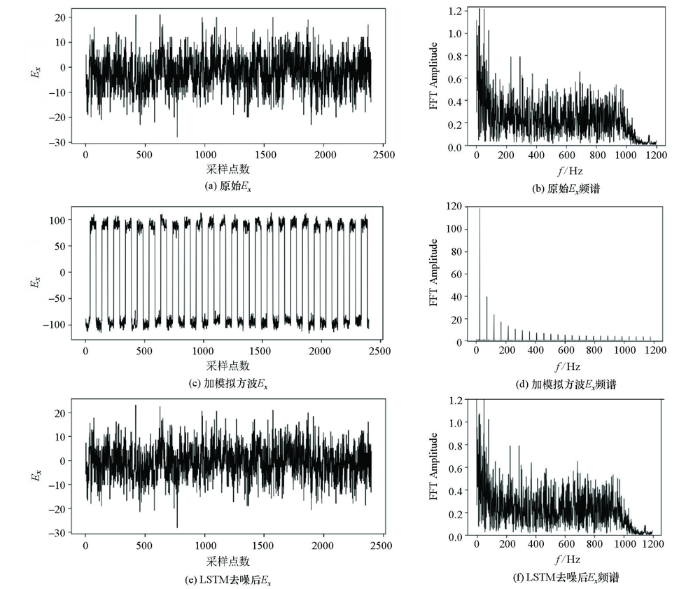
选取陕西省宁强县某地2020年10月16日使用MTU-5A大地电磁仪所采集的无明显人文干扰且阻抗估计稳定的Ex通道时间序列数据段作为测试信号,数据长24 000个点,采样率2 400 Hz,由于数据过长故截取其中1 s(2 400个点)进行展示(图6)。给测试信号叠加一主频24 Hz,振幅为该段测试信号最大值与最小值之差1.5倍的方波噪声作为仿真含噪信号(图6c),用训练好的LSTM网络进行去噪试验。由于天然大地电磁信号的复杂性,在实际使用LSTM网络提取一次大地电磁信号后,残余噪声里还含有部分低频有效信号,可以使用网络进行多次提取,一定程度上可以减小信号损失,但同时也会引入更多的噪声,应该具体情况具体分析。本文所有去噪均为网络提取一次的结果。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   仿真信号片段去噪前后对比

Fig.6   Comparison of Simulation signal fragment before and after denoising


由图6a、b可以看出原始时间序列片段无明显人文干扰,频谱均匀分布,无明显干扰频段,叠加仿真噪声后时间序列基本被方波所淹没,几乎无法分辨出大地电磁信号(图6c),频谱呈现出明显的方波各级谐波频谱特征,且离主频越远幅值越小(图6d)。经LSTM网络去噪后的时间序列与原始时间序列的NCC高达0.971 8,较好地还原了信号,频谱也恢复了原始信号的特征,达到了去噪的目的(图6e、f)。

使用最小二乘法进行阻抗估计。仿真信号未去噪前阻抗结果极不稳定,电阻率曲线在265 Hz、115 Hz和22.5 Hz频点有较大偏离(图7a),阻抗相位曲线在229 Hz、159 Hz、115 Hz和22.5 Hz频点处有较大偏离(图7b);这些频点基本都在方波噪声的各次谐波频率附近,且随着频率升高干扰逐渐减小。LSTM网络去噪后,几处方波噪声影响的频点数据均得到了较好改善,除了离噪声主频较近的22.5 Hz频点附近有能量损失外,其余频点几乎与原始数据重合(图7a、b),说明了本文方法可以有效抑制方波噪声并改善阻抗估计质量。

图7

新窗口打开| 下载原图ZIP| 生成PPT

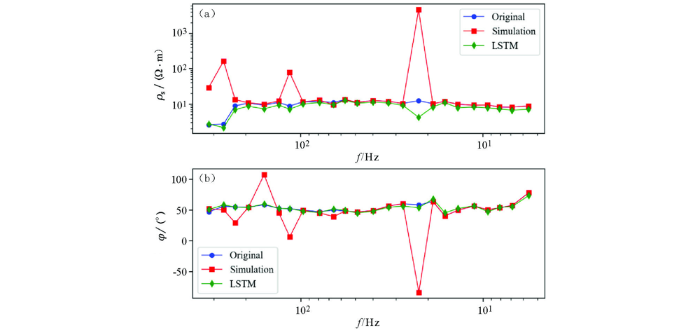
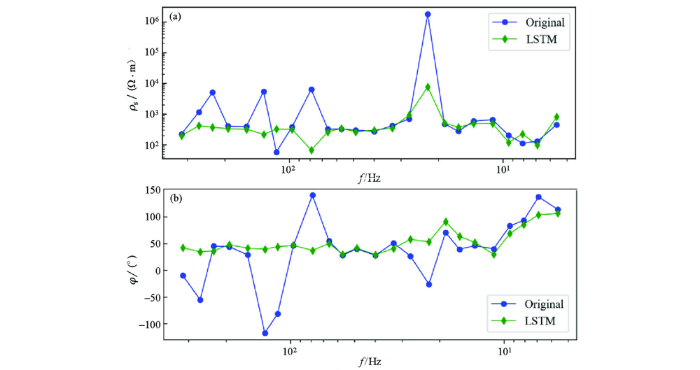
图7   仿真信号去噪前后电阻率、阻抗结果对比

Fig.7   Comparison of resistivity and impedance before and after denoising of simulated signals


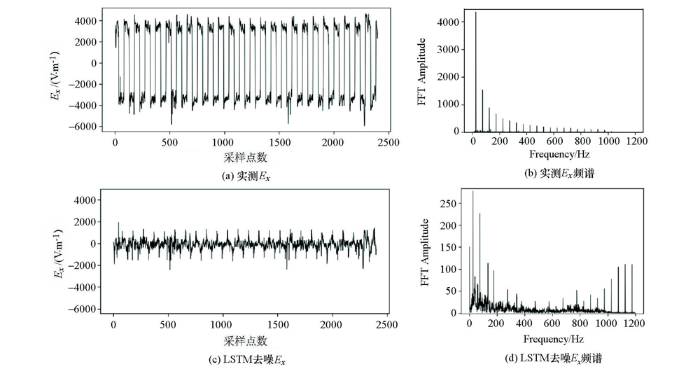
3.2 实测含噪信号去噪

选取陕西省旬阳市某地2021年4月27日使用MTU-5A大地电磁仪采集的实测含方波噪声Ex通道数据段进行实际去噪试验。该数据段长2 400个点,采样率2 400 Hz,由于受附近用电设备的干扰,该段数据表现出典型的含方波噪声大地电磁时间序列特征,噪声已基本将原始信号淹没,频谱被方波各次谐波特征所占据(图8a、b)。经LSTM网络去噪后,时间序列更加接近大地电磁原始信号的时频特征,除高频和低频有残存的方波干扰外,大部分方波干扰被有效抑制(图8c、d)。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   实测信号去噪前后对比

Fig.8   Comparison of measured signals before and after denoising


使用最小二乘法进行阻抗估计。未处理的原始实测信号电阻率及阻抗相位多处频点偏移较大,特别是中高频段数据严重畸变,不连续,无法进行下一步处理。用本文方法去噪后多处干扰频点恢复正常,特别是中高频数据变得稳定连续,由于去噪作用的影响,低频段数据有部分能量损失,电阻率值有小幅度波动(图9a),但是总体来看电阻率曲线和阻抗相位曲线变得更加稳定连续,阻抗质量得到了较好改善(图9a、b)。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   实测信号去噪前后电阻率、阻抗对比

Fig.9   Comparison of resistivity and impedance before and after denoising of measured signals


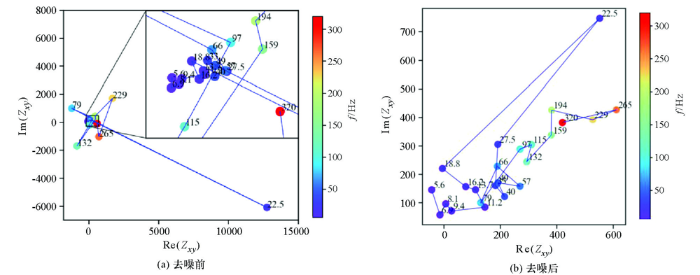
为了进一步评价实测信号去噪效果在此引入奈奎斯特图[22-23],在无噪声干扰条件下,大地电磁阻抗的奈奎斯特图是从低频到高频呈顺时针展布的连续光滑曲线,一旦某个频点受到干扰该频点将会脱离这种趋势,所以可以根据奈奎斯特图是否更具有这种趋势来评判去噪效果。去噪前,实测信号阻抗的奈奎斯特图特征比较混乱,特别是在22.5 Hz、79 Hz、132 Hz、229 Hz等频点处严重脱节,几乎无法识别出其顺时针旋转特征(图10a)。经本文方法去噪后,除22.5 Hz较其他频点偏离较大之外,其余频点虽然也不是光滑连续分布,但是基本滤除了大尺度方波对阻抗的干扰,奈奎斯特图总体趋势基本符合从低频到高频顺时针展布的特征(图10b),与去噪前相比阻抗结果更加稳定和合理。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   实测信号去噪前后的奈奎斯特图对比

Fig.10   Comparison of Nyquist diagrams before and after denoising of measured signals


4 结论与建议

与前人将噪声作为LSTM网络的期望输出不同的是,本文采用大地电磁信号本身作为网络期望输出,用训练好的网络进行了仿真含方波噪声和实测含方波噪声的大地电磁时间序列去噪测试,结果表明本文所提方法能有效消除方波噪声干扰,改善阻抗估计结果,为深度学习在大地电磁时间序列去噪领域的应用提出了新思路。

本文所提方法仍具有局限性:一是本文只讨论了方波噪声的处理,对于其他典型的强干扰噪声也可以借鉴本文的思路进行处理,但是怎样让网络适应不同类型的噪声需要研究;二是由于天然大地电磁信号的非平稳性和随机性[24-25],在选取训练数据时不能很好地囊括所有信号特征,只有当待处理数据的信号特征与训练网络所用大地电磁信号特征相似时才可以有效去除噪声,当遇到网络未学习过的信号时去噪效果就会大打折扣,所以怎样更合理地构建训练神经网络所需的数据集将是下一步需要解决的问题。

致谢

感谢中国地质调查局西安矿产资源调查中心郝子琼对本文网络训练的支持!

参考文献

孙洁, 晋光文.

大地电磁测深资料的噪声干扰

[J]. 物探与化探, 2000, 24(2):119-127.

[本文引用: 1]

Sun J, Jin G W.

Noise interference of magnetotelluric data

[J]. Geophysical and Ceochemical Exploration, 2000, 24(2):119-127.

[本文引用: 1]

汤井田, 徐志敏, 肖晓, 等.

庐枞矿集区大地电磁测深强噪声的影响规律

[J]. 地球物理学报, 2012, 55(12):4147-4159.

[本文引用: 1]

Tang J T, Xu Z M, Xiao X, et al.

Effect rules of strong noise on magnetotelluric (MT) sounding in Luzong ore cluster area

[J]. Chinese Journal of Geophysics, 2012, 55(12):4147-4159.

[本文引用: 1]

严家斌. 大地电磁信号处理理论及方法研究[D]. 长沙: 中南大学, 2003.

[本文引用: 1]

Yan J B. The study on theory and method of magnetotelluric signal processing[D]. Changsha: Central South University, 2003.

[本文引用: 1]

蔡建华, 汤井田, 王先春.

基于经验模态分解的大地电磁资料人文噪声处理

[J]. 中南大学学报:自然科学版, 2011, 42(6):1786-1790.

[本文引用: 1]

Cai J H, Tang J T, Wang X C.

Human noise elimination for magnetotelluric data based on empirical mode decomposition

[J]. Journal of Central South University:Science and Technology, 2011, 42(6):1786-1790.

[本文引用: 1]

汤井田, 李晋, 肖晓, 等.

数学形态滤波与大地电磁噪声压制

[J]. 地球物理学报, 2012, 55(5):1784-1793.

[本文引用: 1]

Tang J T, Li J, Xiao X, et al.

Mathematical morphology filtering and noise suppression of magnetotelluric sounding data

[J]. Chinese Journal of Geophysics, 2012, 55(5):1784-1793.

[本文引用: 1]

汤井田, 刘祥, 周聪.

仿真方波的大地电磁远参考去噪研究

[J]. 物探化探计算技术, 2014, 36(5):513-520.

[本文引用: 1]

Tang J T, Liu X, Zhou C.

Simulation of square waveform de-noising research of magnetotelluric with a remote reference

[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2014, 36(5):513-520.

[本文引用: 1]

王辉, 魏文博, 金胜, 等.

基于同步大地电磁时间序列依赖关系的噪声处理

[J]. 地球物理学报, 2014, 57(2):531-545.

[本文引用: 1]

Wang H, Wei W B, Jin S, et al.

Removal of magnetotelluric noise based on synchronous time series relationship

[J]. Chinese Journal of Geophysics, 2014, 57(2):531-545.

[本文引用: 1]

汤井田, 李广, 周聪, 等.

基于字典学习的音频大地电磁数据处理

[J]. 地球物理学报, 2018, 61(9):3835-3850.

[本文引用: 1]

Tang J T, Li G, Zhou C, et al.

Denoising AMT data based on dictionary learning

[J]. Chinese Journal of Geophysics, 2018, 61(9):3835-3850.

[本文引用: 1]

李晋, 张贤, 蔡锦.

利用变分模态分解(VMD)和匹配追踪(MP)联合压制音频大地电磁(AMT)强干扰

[J]. 地球物理学报, 2019, 62(10):3866-3884.

[本文引用: 1]

Li J, Zhang X, Cai J.

Suppression of strong interference for AMT using VMD and MP

[J]. Chinese Journal of Geophysics, 2019, 62(10):3866-3884.

[本文引用: 1]

王昊, 严加永, 付光明, 等.

深度学习在地球物理中的应用现状与前景

[J]. 地球物理学进展, 2020, 35(2):642-655.

[本文引用: 1]

Wang H, Yan J Y, Fu G M, et al.

Current status and application prospect of deep learning in geophysics

[J]. Progress in Geophysics, 2020, 35(2):642-655.

[本文引用: 1]

李瑞友, 张淮清, 吴昭.

基于在线惯序极限学习机的瞬变电磁非线性反演

[J]. 物探与化探, 2021, 45(4):1048-1054.

[本文引用: 1]

Li R Y, Zhang H Q, Wu Z.

Online sequential extreme learning machine for transient electromagnetic nonlinear inversion

[J]. Geophysical and Geochemical Exploration, 2021, 45(4):1048-1054.

[本文引用: 1]

王逸宸, 柳林涛, 许厚泽.

基于卷积神经网络识别重力异常体

[J]. 物探与化探, 2020, 44(2):394-400.

Wang Y C, Liu L T, Xu H Z.

The identification of gravity anomaly body based on the convolutional neural network

[J]. Geophysical and Geochemical Exploration, 2020, 44(2):394-400.

韩卫雪, 周亚同, 池越.

基于深度学习卷积神经网络的地震数据随机噪声去除

[J]. 石油物探, 2018, 57(6):862-869.

Han W X, Zhou Y T, Chi Y.

Deep learning convolutional neural networks for random noise attenuation in seismic data

[J]. Geophysical Prospecting for Petroleum, 2018, 57(6):862-869.

王鹤, 蒋欢, 王亮, 等.

大地电磁人工神经网络反演

[J]. 中南大学学报:自然科学版, 2015, 46(5):1707-1714.

Wang H, Jiang H, Wang L, et al.

Magnetotelluric inversion using artificial neural network

[J]. Journal of Central South University:Science and Technology, 2015, 46(5):1707-1714.

赵文举, 刘云祥, 陶德强, 等.

BP神经网络磁性体顶面埋深预测方法

[J]. 石油地球物理勘探, 2020, 55(5):1139-1148.

[本文引用: 1]

Zhao W J, Liu Y X, Tao D Q, et al.

Prediction of magnetic body top based on BP neural network

[J]. Oil Geophysical Prospecting, 2020, 55(5):1139-1148.

[本文引用: 1]

Manoj C, Nagarajan N.

The application of artificial neural networks to magnetotelluric time-series analysis

[J]. Geophysical Journal International, 2003, 152(2):409-423.

[本文引用: 1]

许滔滔, 王中兴, 肖卓伟, 等.

基于LSTM 循环神经网络的大地电磁工频干扰压制

[J]. 地球物理学进展, 2020, 35(5):2016-2022.

[本文引用: 1]

Xu T T, Wang Z X, Xiao Z W, et al.

Magnetotelluric power frequency interference suppression based on LSTM recurrent neural network

[J]. Progress in Geophysics, 2020, 35(5):2016-2022.

[本文引用: 1]

王斯昊, 何兰芳.

基于LSTM循环神经网络的MT时间序列去噪可行性分析

[C]// 中国地球物理学会地球物理技术委员会第九届学术会议—全域地球物理探测与智能感知学术研讨会会议摘要集, 2021.

[本文引用: 1]

Wang S H, He N F.

Feasibility analysis of the LSTM based denoising to MT time series

[C]// The 9th Conference of Geophysical Technology,Chinese Geophysical Society—Abstracts of Symposium on Full-Space Geophysical Exploration and Intelligent Sensing, 2021.

[本文引用: 1]

汪凯翔, 黄清华, 吴思弘.

长短时记忆神经网络在地电场数据处理中的应用

[J]. 地球物理学报, 2020, 63(8):3015-3024.

[本文引用: 1]

Wang K X, Huang Q H, Wu S H.

Application of long short-term memory neural network in geoelectric field data processing

[J]. Chinese Journal of Geophysics, 2020, 63(8):3015-3024.

[本文引用: 1]

Hochreiter S, Schmidhuber J.

Long short-term memory

[J]. Neural Computation, 1997, 9(8):1735-1780.

PMID:9377276      [本文引用: 1]

Learning to store information over extended time intervals by recurrent backpropagation takes a very long time, mostly because of insufficient, decaying error backflow. We briefly review Hochreiter's (1991) analysis of this problem, then address it by introducing a novel, efficient, gradient-based method called long short-term memory (LSTM). Truncating the gradient where this does not do harm, LSTM can learn to bridge minimal time lags in excess of 1000 discrete-time steps by enforcing constant error flow through constant error carousels within special units. Multiplicative gate units learn to open and close access to the constant error flow. LSTM is local in space and time; its computational complexity per time step and weight is O(1). Our experiments with artificial data involve local, distributed, real-valued, and noisy pattern representations. In comparisons with real-time recurrent learning, back propagation through time, recurrent cascade correlation, Elman nets, and neural sequence chunking, LSTM leads to many more successful runs, and learns much faster. LSTM also solves complex, artificial long-time-lag tasks that have never been solved by previous recurrent network algorithms.

Kingma D, Ba J.

Adam:A method for stochastic optimization

[J]. Computer Science, 2014(12).doi: 10.48550/arXiv.1412.6980.

[本文引用: 1]

Uhm J, Heo J, Min D J, et al.

Imaging strategies to interpret 3-D noisy audio-magnetotelluric data acquired in Gyeongju South Korea:data processing and inversion

[J]. Geophysical Journal International, 2021, 225(2):744-758.

DOI:10.1093/gji/ggab002      URL     [本文引用: 1]

Yang Y, Wang X, Han J, et al.

Magnetotelluric transfer function distortion assessment using Nyquist diagrams

[J]. Journal of Applied Geophysics, 2019, 160:218-228.

DOI:10.1016/j.jappgeo.2018.11.018      [本文引用: 1]

Magnetotelluric (MT) inversion is using impedance data as input data, which is traditionally presented via the apparent resistivity and impedance phase. Since high-quality MT data are necessary to improve the reliability of inversion results, the distortions in the curves should be assessed and removed. Usually, this smoothing procedure acts individually on the apparent resistivity and phase and does not consider the dispersion relationship between the real and imaginary parts of the impedance. Therefore, how to assess the distortion while retaining the inherent relationship in the impedance should be addressed. In this study, Nyquist diagrams were used as a tool to illustrate the inherent feature of the MT complex response. The MT impedances of 2-D and 3-D models were computed and illustrated in the corresponding diagrams. From these curves, we found that the Nyquist curves or part of them are continuous and smooth. When the model is 1-D or 2-D, Z(xy) and Z(yx) try to stretch around a line at a 45 degrees slope, whereas in the 3-D case, the Nyquist diagrams of the full impedance elements rotate clockwise from low to high frequencies. If the frequency is high or low enough, the curves of Z(xx) and Z(yy) become approximate ellipses. The phases of Z(xx) and z(yy) are also out of scope (-pi,pi), which is beyond the traditional knowledge of the phase, which making data distortion removal in the phase confusing. Cole-Cole model could be used to explain above features. And these features behind the Nyquist diagrams could be used as tools to guide the distortion removal in the MT complex response in the field. When MT impedance data are not severely distorted, it is possible to recover high-quality data when obeying the following two rules: (1) both the amplitude and phase should be smooth and (2) the Nyquist curve of the complex response should also be smooth or at least smooth in segments. (C) 2018 Published by Elsevier B.V.

王书明, 王家映.

大地电磁信号统计特征分析

[J]. 地震学报, 2004, 26(6):669-674.

[本文引用: 1]

Wang S M, Wang J Y.

Analysis on statistic characteristics of Magnetotelluric signal

[J]. Acta Seismologica Sinica, 2004, 26(6):669-674.

[本文引用: 1]

Neukirch M, Garcia X.

Nonstationary magnetotelluric data processing with instantaneous parameter

[J]. Journal of Geophysical Research:Solid Earth, 2014, 119(3):1634-1654.

DOI:10.1002/2013JB010494      URL     [本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com