E-mail Alert Rss
 

物探与化探, 2022, 46(4): 1011-1020 doi: 10.11720/wtyht.2022.1404

生态地质调查

半干旱区有机质与全氮空间变异的尺度效应特征——以延安市为例

王鹏,1, 赵君,1, 刘拓1, 周一凡2, 魏锦萍1, 王磊1

1.中国地质调查局 西安地质调查中心西北地质科技创新中心,陕西 西安 710054

2.西安市勘察测绘院,陕西 西安 710059

Scale effects of spatial variations in SOM and STN in semi-arid regions: A case study of Yan'an

WANG Peng,1, ZHAO Jun,1, LIU Tuo1, ZHOU Yi-Fan2, WEI Jin-Ping1, WANG Lei1

1. Xi'an Center of China Geological Survey Northwest China Center for Geoscience Innovation,Xi'an 710054,China

2. Xi'an Institute of Prespecting and Mapping,Xi'an 710059,China

通讯作者: 赵君(1981-),男,高级工程师,主要从事地球化学调查研究工作。Email:28611635@qq.com

责任编辑: 蒋实

收稿日期: 2021-07-20   修回日期: 2021-09-29  

基金资助: 中国地质调查局基础地质调查项目“西北地区自然资源动态监测与风险评估”(DD20211393)
“新疆耕地区土地质量地球化学调查”(DD20190521)

Received: 2021-07-20   Revised: 2021-09-29  

作者简介 About authors

王鹏(1986-),男,河南杞县人,高级工程师,主要从事土地质量地球化学调查方面的研究工作。Email: 331559202@qq.com

摘要

以高密度采样数据为数据集,经重采样分析,模拟不同尺度的采样空间分布场景,采用莫兰指数、半方差函数值和分形维数 F D等空间分析方法,探讨土壤有机质和全氮空间变异的尺度效应特征,并分析其影响因素的尺度间转换关系。结果表明:随着尺度增大,空间集聚性降低,有机质和全氮含量空间总变异先增大后趋于稳定,但随机性变异逐渐减少,结构性变异先增大后减少。小尺度产生的空间变异中的随机变异占比较多,结构变异占比较少,而大尺度则相反。不同的影响因素对有机质和全氮空间变异具有不同的区分度,高程的区分度最小;土壤类型、植被指数、年均气温、湿度等影响因素的区分度次之;降水量的区分度最大。有机质和全氮空间变异影响因素具有尺度特征,随着尺度增大,小尺度因素引起的随机变异逐渐减少,而大尺度因素引起的结构性变异先增大后减弱,直至转换为相对的小尺度因素;各影响因素对土壤有机质和全氮含量的影响协同机制在尺度间差异较大,引起随机变异和结构变异出现尺度间消长,导致空间变异呈现出先减少后趋于平稳的变化规律。

关键词： 采样尺度; 空间变异; 分形维数; 半方差函数; 有机质; 全氮; 半干旱区

Abstract

Taking high-density sampling data as a dataset, the sampling spatial distribution scenarios on different scales were simulated through resampling analysis. Spatial analysis methods, such as Moran's I index, semi-variance function value, and fractal dimension FD, were used to explore the scale effects of spatial variations in soil organic matter (SOM) and soil total nitrogen (STN) and to analyze the conversion of influencing factors between different scales. The results are as follows. With an increase in scale, the spatial agglomeration decreased, and the spatial variation of SOM and STN in general increased first and then tended to be stable. By contrast, the random variation decreased gradually and the structural variation increased first and then decreased as the scales increased. The spatial variation generated on small scales consisted of a large proportion of random variation and a small proportion of structural variation, while the opposite is true on large scales. Different influencing factors had different distinguishing degrees for the spatial variations in SOM and STN. Their distinguishing degrees were in the order of height<factors such as soil type, vegetation index, annual average temperature, and humidity<precipitation. The influencing factors of the spatial variations in SOM and STN had scale effects. Specifically, with an increase in scale, the random variation caused by small-scale factors decreased gradually, while the structural variation caused by large-scale factors increased first and then weakened until the large-scale factors were transformed into relatively small-scale factors. The coordination mechanism of the effects of each factor on the SOM and STN contents was quite different between different scales, causing the random and structural variations to fluctuate between different scales. As a result, the spatial variations showed the law of decreasing first and then tending to stabilize.

Keywords： sampling scale; spatial variation; fractal dimension; semi-variance function; SOM; STN; semi-arid regions

PDF (5421KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王鹏, 赵君, 刘拓, 周一凡, 魏锦萍, 王磊. 半干旱区有机质与全氮空间变异的尺度效应特征——以延安市为例[J]. 物探与化探, 2022, 46(4): 1011-1020 doi:10.11720/wtyht.2022.1404

WANG Peng, ZHAO Jun, LIU Tuo, ZHOU Yi-Fan, WEI Jin-Ping, WANG Lei. Scale effects of spatial variations in SOM and STN in semi-arid regions: A case study of Yan'an[J]. Geophysical and Geochemical Exploration, 2022, 46(4): 1011-1020 doi:10.11720/wtyht.2022.1404

0 引言

土壤是具有地理空间和属性空间连续性[1]的不均匀自然体。土壤形成、发育与演化过程中各成土因素在不同尺度上的交互作用,以及受到的各种随机因素(耕作、灌溉、施肥)的影响,使土壤特性空间分布呈现出不同程度的异质性[2⇓-4]和相关性[5],具有一定的渐变性和模糊性,蕴含着多层次的变化[6]。国内外多位学者已针对土壤特性的空间变异开展了相关研究,研究内容多为土壤养分[1,7-8]、重金属污染[6,9-10]、有机质[11-12]等特性的空间变异影响因素分析,研究尺度涉及田块、乡镇、县域等中、小尺度[9,13-14],研究方法主要有空间变异理论[5]、分形维数[2,15]、地统计学[16]等,剖析了土壤特性的空间变异结构组成,定量化表示了结构变异和随机变异占比。总之,土壤特性空间变异(随机变异和结构变异)具有多尺度变异特征[7-8],尤其是成窄斜带状分布于内蒙古、陕西、甘肃一带的我国半干旱气候区,其气候、植被等成土影响因素在纬向、经向的梯度差异明显,土壤特性具有明显的地带性[17],但针对该区域土壤特性空间变异的研究较为缺乏,结构性和随机性变异多为单尺度的描述或为少数尺度的对比研究,其在尺度间的变化规律以及主导影响因素转换关系尚不清楚。

由于半干旱气候区土壤中的K、P含量处于中等、较丰富等级,而有机质(SOM)和全氮(STN)的含量处于缺乏和较缺乏等级[18],是制约土壤质量提高的限制性因素[19]。因此,笔者选取土壤有机质和全氮为指标,以处于半干旱区典型地区的延安市为例,利用高密度土地质量地球化学调查数据,抽取不同尺度数据集,模拟不同尺度采样分布场景,采用空间变异分析的理论与方法来探讨半干旱区的土壤有机质和全氮空间变异的尺度效应特征,并分析主导影响因素在尺度间的转换关系,旨在为该区土壤采样设计,碳、氮储量估算以及尺度转换提供理论依据。

1 研究方法

有机质和全氮的空间结构具有多尺度特征,为揭示其空间尺度结构性、随机性、不规则性、独立性和相关性的变化规律[15],采用莫兰指数进行土壤中有机质和全氮的空间自相关及变异结构分析[11],显现研究变量空间集聚性随尺度的变化概况;利用半方差函数及分形维数来模拟其空间结构随尺度的变化趋势,以揭示空间随机变异与结构变异的消长规律。

1.1 空间自相关

莫兰指数是检验某一要素属性值在空间上是否相关联的最常用统计量,主要用于描述区域性变量的整体分布状况,以揭示空间区域性变量的结构形态,其计算公式为[20]:

I=∑i=1n∑j=1nwij(xi-x¯)(xj-x¯)S2∑i=1n∑j=1nwij
S2=1n∑i=1n(xi-x¯)2 。

式中:I为莫兰指数值;n为区域空间单元总数;xi、xj为在地理单元i和j上的观察值;x¯为平均值;S2为方差;wij为权重矩阵,即相邻之间的权重为1,不相邻的权重为0。

莫兰指数的值域为[-1,1],莫兰指数值大于0,表明空间正相关,其值越大,空间相关性越明显;莫兰指数值小于0,表明空间负相关,其值越小,空间差异性越大;莫兰指数值为0,表明空间随机性。

1.2 空间变异

1.2.1 半方差函数

半方差函数也称空间变异函数,定义为取样间隔为h时的样本值方差数学期望的一半,其计算公式[21]为:

γ(h)=12N(h)∑i=1N(h)[Z(xi)-Z(xi+h)]2 。

式中:γ(h)为取样间隔为h时的半方差函数值;h为取样间隔距离;N(h)为以取样间隔为h的所有观测点成对数目;Z(xi)、Z(xi+h)为取样间隔为h的两组实测值。

半方差函数值随取样间隔h的增大而增加,当达到一定距离后,稳定在某极限值附近,可以获得块金值C0、基台值C0+C、偏基台值C和变程A0参数,以用于衡量变量的空间结构。其中,C0为随机变异;C为结构变异;C0+C为总变异;A0表示半方差函数值达到基台值时的取样间隔距离。块基比C0/(C0+C)小于25%,说明变量间为强空间相关;在25%~75%之间,为中等空间相关;大于75%,弱空间相关。

1.2.2 分形维数

分形维数FD是对事物复杂程度的一种量度[15],可利用变异函数的双对数关系lgγ(h)∝lgh的斜率对其进行定义,以度量土壤变量空间异质性特征,其计算公式为[2,16,21]:

FD=2-H
H=12lgγ(h)∝lgh 。

式中:FD为分形维数;H为斜率;γ(h)为取样间隔为h的半方差函数值;h为取样间隔距离。

由式(4)、(5)可知,H的值域为[0,1),则FD的值域为(1,2]。FD越小,随机变异占比小,结构变异占比大;FD越大,随机变异占比大,结构变异占比小。

2 实例研究

2.1 研究区域

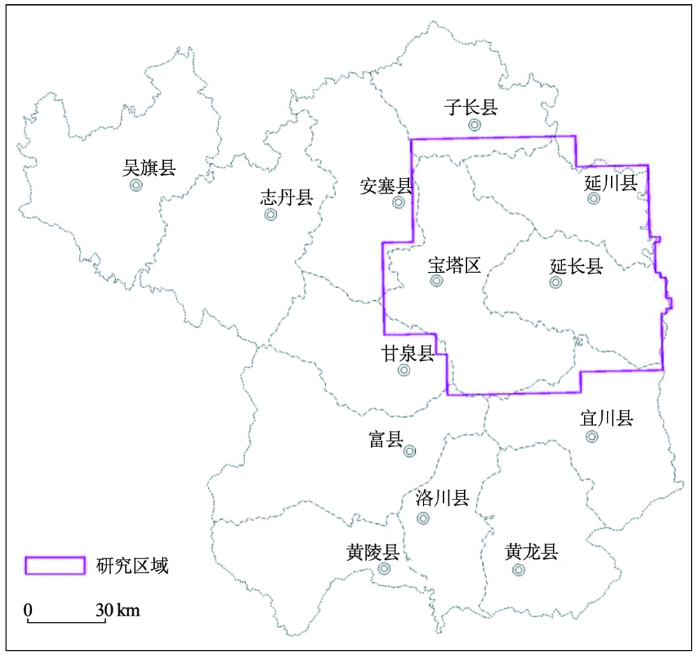
研究区域位于陕西省延安市宝塔区、延川县、延长县及周边区域(图1),处于东经109°15'21.60″~110°30'25.20″,北纬36°11'49.20″~37°05'52.80″之间,属半湿润半干旱大陆性季风气候,年均降水量为469.58~531.83 mm,年均湿度为58.74%~64.29%,年均日照时间为2 300~2 700 h,年均气温为9.23~10.80 ℃。该区为黄土高原丘陵沟壑区,地势西北高,东南低,海拔499~2 000 m。土壤类型主要为黄绵土、新积土、红黏土、粗骨土等,土壤质地以轻壤土和砂壤土为主。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   研究区域位置

Fig.1   Location of the study area


2.2 数据来源与处理

2.2.1 数据来源

利用延安市宝塔区、延川县、延长县等地2018年土地质量地球化学调查成果,获得了8 462个采样点的有机质和全氮分析数据、GPS横纵坐标和海拔数据。采样密度为1个点/km2,单样按梅花法取3~5个点,并遵从代表性、均匀性、合理性和多点混合的原则,取0~20 cm土层的土样,每个样品质量1 000 g左右。同时,采样时注重避开粪堆、新近堆积土等点状污染物,并去掉植物根系和岩石碎块,自然风干后,过20目尼龙筛,由自然资源部安徽地质测试实验室进行测试,其中,有机质采用硫酸亚铁铵容量法(VOL)分析,全氮采用凯氏丹蒸馏酸碱滴定(VOL)分析,分析质量均符合《地质矿产实验室测试质量管理规范》(DZ0130.1~130.13-94)要求。

降雨量、气温、湿度等气象数据来源于中国气象数据服务中心2018年连续数年和连续数天的数据集,插值得到研究区分辨率为30 m×30 m的气象要素网格数据层。植被指数数据来源于lpdaac(land process distributed active archive center)提供的16天mod13q1数据产品,分辨率为250 m×250 m。土壤类型数据来源于《1∶100万中国土壤数据库》。

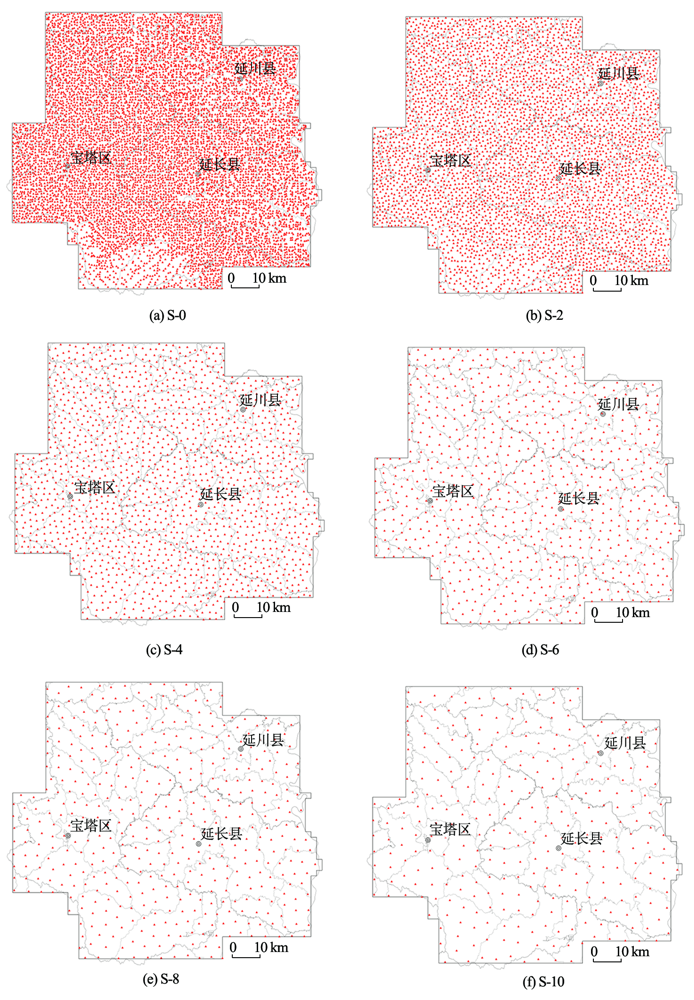
2.2.2 重抽样及数据处理

采样点数量对揭示有机质和全氮含量的空间分布特征存在较大影响[22],采样尺度可通过影响采样点的数量及其空间布局改变空间变异分析的结果[7]。土地质量地球化学调查为网格采样,其原始数据为高密度数据集,可以依据不同采样距离对其进行重抽样分析,提取10个子数据集(表1),来模拟不同采样尺度的采样点位空间分布(图2)场景[23],以反映空间尺度的变化[6]。

表1   重采样后不同间距尺度对应关系

Table 1  Relationship of different spacing after resampling analysis

尺度S-0S-1S-2S-3S-4S-5S-6S-7S-8S-9S-10
指定距离/m500100015002000250030003500400045005000
样点数84628037406223011463936666486380302249

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   不同尺度采样分布

Fig.2   Sampling distribution at different scales


为避免半方差函数产生畸变,出现比例效应[6,11,19],降低拟合精度,需要针对各采样尺度数据集采用x±3δ法剔除特异值(x为数据平均值,δ为标准差),并经非参数检验法(D检验或W检验)检验。检验后发现本次数据均不符合正态分布(P<0.05),但经对数转换后,各尺度有机质、全氮的数据集符合或近似正态分布(P>0.05),可进行空间结构分析。

同时,依据采样点的重采样距离,分别对降雨量、气温、湿度以及植被指数等栅格数据进行重采样,以确保数据尺度统一。

3 结果与讨论

3.1 空间分析结果

3.1.1 统计分析结果

变异系数和均值均可反映变量数据的总体变异程度[11]。各尺度有机质、全氮含量的均值分别处于(0.455 3~0.490 3)×10-3、(0.4869~0.5127)×10-3(图3a),依据《土地质量地球化学评价规范》(DZ/T 0295—2016),均为五等,属于缺乏水平。各尺度有机质、全氮的含量变异系数较为集中,分别处于39.36%~51.24%、28.93%~35.99%,属于中等变异[20-21](图3b),但是有机质的变异系数高于全氮。随着尺度增大,有机质和全氮含量的均值和变异系数具有相似的变化趋势,呈现出先增大后趋于稳定的变化规律。

图3

新窗口打开| 下载原图ZIP| 生成PPT

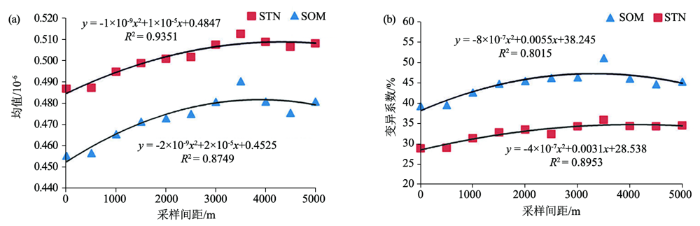
图3   不同采样尺度均值(a)、变异系数(b)与尺度的散点分布

Fig.3   Scatter diagram of variation mean value(a) and codfficients(b) at different scales


无论均值还是变异系数,尺度S-0、S-1处为低值,尺度S-6、S-7、S-8处为高值,经独立样本Kruskal-Wallis非参数检验(所有成对比较)发现,两项参数均具有显著差异(P<0.05),但其他尺度间差异不显著。

3.1.2 空间自相关结果

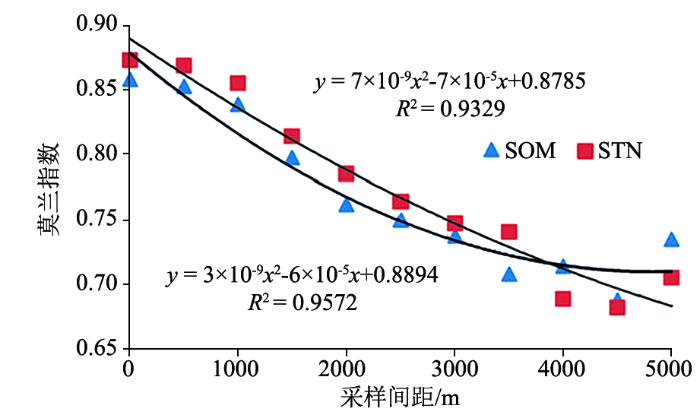
将各尺度有机质、全氮的含量进行全局莫兰指数计算,经标准化,Z值得分均超过临界值1.65,显著性强(P<0.01),且有机质和全氮的莫兰指数处于0.68~0.87(图4),为强空间相关。但随采样尺度增大,有机质和全氮的空间聚集性先变弱后趋于稳定。同时,在尺度S-0~S-7下,全氮具有更强的空间相关性;而在尺度S-8 ~S-10下,有机质的空间相关性较强。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同采样尺度Moran’s I指数与尺度的散点分布

Fig.4   Scatter diagramof Moran’s I at different scales


3.1.3 空间变异结果

各尺度的有机质和全氮含量半方差函数在各方向上均具有内蕴平稳性,如:以采样距离为0和5 000 m为例,计算有机质和全氮的含量在0°、45°、90°和135°四个方向上的半方差函数值(表2),C0、C0+C和C0/(C0+C)在各方向上的差距均较小,半方差结构在各方向上基本相同,各向同性,并类推至其他尺度,得出相同结果。

表2   有机质和全氮半方差结构异质性分析

Table 2  Semivariogram heterogeneity analysis of SOM and STN

指标采样距离/m方向/(°)拟合模型C0C0+C[C0/(C0+C)]/%
有机质00G0.03680.12860.2862
45G0.03660.12870.2845
90G0.03680.12870.2859
135G0.03650.12860.2839
50000G0.02540.11780.2156
45G0.02530.11770.2149
90G0.02550.11780.2164
135G0.02560.11830.2164
全氮00G0.01970.06980.2822
45G0.01960.06960.2816
90G0.01980.06980.2837
135G0.01990.06990.2847
50000G0.01250.07680.1628
45G0.01260.07690.1640
90G0.01260.07690.1642
135G0.01260.07690.1633

新窗口打开| 下载CSV


各尺度的最佳理论模型均为高斯模型,决定系数最大,残差最小(表3),拟合精度高(P<0.05),有确定的块金值、基台值和变程,客观地反映了有机质和全氮的空间变异结构特征。

表3   不同尺度有机质和全氮的半方差函数及分形维数

Table 3  Semi-variogram and fractal dimension of SOM and STN at different scales

项目采样
距离/m		拟合
模型		C0C0+C[C0/(C0+
C)]/%		变程/m决定
系数R2		残差
RSS		分形
维数FD
有机质0G0.03370.111430.25454000.9751.52×10-41.759
500G0.03380.111630.29450000.9771.18×10-31.758
1000G0.03210.124225.85469000.9811.49×10-41.730
1500G0.03010.136222.10494000.9851.49×10-41.705
2000G0.02770.131421.08475000.9861.42×10-41.690
2500G0.02710.134220.19477000.9871.32×10-41.676
3000G0.0250.125020.00472000.9851.38×10-41.673
3500G0.0260.141018.44503000.9919.64×10-51.669
4000G0.02180.110619.71444000.9889.80×10-51.649
4500G0.02360.111221.22460000.9926.39×10-51.677
5000G0.02540.117821.56499000.9898.25×10-51.660
全氮0G0.01970.069828.22461000.984.64×10-51.747
500G0.01960.070127.96458000.9824.44×10-51.744
1000G0.0190.076724.77462000.9854.66×10-51.721
1500G0.01750.082521.21484000.9949.30×10-51.694
2000G0.01640.080020.50459000.9868.36×10-51.683
2500G0.01570.083218.87470000.9904.34×10-51.660
3000G0.01410.077518.19471000.9894.10×10-51.653
3500G0.01460.087716.65489000.9911.46×10-51.637
4000G0.01210.072616.67447000.9922.79×10-51.620
4500G0.01370.073818.56471000.9922.56×10-51.650
5000G0.01250.076816.28509000.9903.38×10-51.623

注:在进行半方差函数拟合及分形维数计算时,不同尺度有机质最大步长距离50 300 m,间隔距离6 000 m;不同尺度全氮的最大步长距离50 900 m,间隔距离6 000 m;拟合模型G为高斯模型。

新窗口打开| 下载CSV


随着尺度变大,变程始终处于45 000~50 000 m区间范围,表明采样点位具有空间相关性的距离是恒定的,不随尺度而变化。但采样尺度的变化对其空间结构的表征存在很大影响[9],各尺度的有机质和全氮含量均具有中、强度空间相关性,空间结构差异较大。随着采样尺度增大,随机变异先减少后趋于稳定,结构变异先增加后降低,块基比C0/(C0+C)呈现出先减小后趋于稳定的变化规律(图5a)。但在各尺度下,有机质的块基比值均较全氮大,表明有机质的随机变异占比较多,结构变异占比较少。

图5

新窗口打开| 下载原图ZIP| 生成PPT

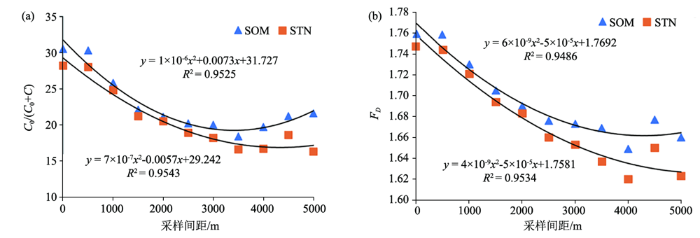
图5   不同采样尺度下有机质和全氮的块基比(a)、分形维数(b)散点分布

Fig.5   Scatter diagram of Nugget-Sill ratio(a) and fractal dimension(b) of SOM and STN at different scales


各尺度有机质和全氮含量的FD值有微小变化,表明采样尺度对其空间变异性具有一定的影响[15]。随着采样尺度增大,有机质、全氮的FD值均出现先减小后趋于稳定的变化规律(图5b),小尺度的变异特征(人为因子引起的随机变异)[3]比例逐渐减少,大尺度的变异特征(结构因子引起的结构变异)比例先增大后趋于稳定。但在各采样尺度下,有机质的FD值均高于全氮,全氮的结构变异占比较高。

3.2 讨论

3.2.1 有机质和全氮含量的空间分布规律

土壤属性的空间变异是尺度的函数[6]。不同采样尺度得到的有机质和全氮含量空间分布格局基本一致(图6),但由于其采样尺度不同,采样点的空间布局不同[7],有机质和全氮含量变化细部特征的表征也会出现尺度间差异。随着尺度增大,采样点数量减少,采样点的间距增大,部分区域的有机质和全氮信息丢失,细部特征的表征越来越粗略,而宏观的纬向地域分异规律越加明显。

图6

新窗口打开| 下载原图ZIP| 生成PPT

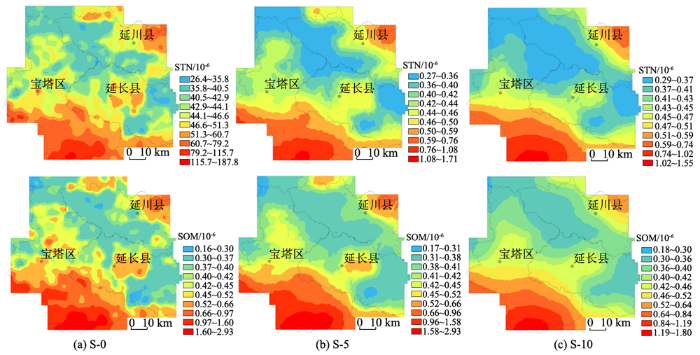
图6   有机质和全氮的含量在S-0、S-5、S-10尺度的空间分布

Fig.6   Spatial distribution of SOM and STN contentsat S-0、S-5、S-10 scales


3.2.2 影响因素的区分度

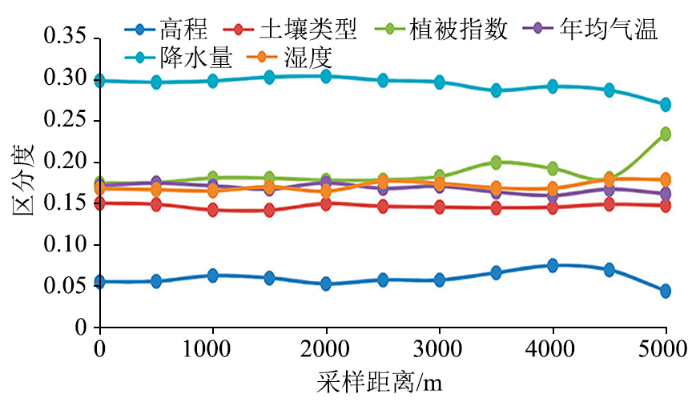
气候、植被、高程、土壤类型是影响有机质和全氮含量的因素[24]。采用基于熵理论的区分度模型[25-26]来计算各影响因素对有机质和全氮含量的区分度(图7),发现不同的影响因素具有不同的区分度,其中高程的区分度最小,土壤类型、植被指数、年均气温、湿度等影响因素次之,降水量的区分度最大。在半干旱区,有机质和全氮含量的生长过程(植物生长)和破坏过程(微生物分解)速率对降水量的响应是积极的[12],对其空间变异具有重要的作用[12],而其他因素的作用则与自身差异程度具有正相关。经分析,研究区的温度(10 ℃)和湿度(60.91%)普遍偏低,降水量空间分布(469.58~531.83 mm)不均匀,在降水量充沛区域,植物生长高于分解,有机质和全氮含量积累;反之,含量消耗。而其他因素,由于其自身差异程度小(如采样点多分布于耕地较为集中的坝地和塬面,高程差异较小;植被多为农作物、经济作物,植被指数差异小;土壤类型多为黄土或次生黄土,成土母质均为风成砂),对有机质和全氮的尺度间分异贡献微乎其微。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   各影响因素对有机质和全氮含量的区分度

Fig.7   Differentiation of SOM and STN content by influencing factors


3.2.3 有机质和全氮含量空间变异的尺度效应

各种影响因素引起有机质和全氮含量出现全部显著差异的尺度不同,如降水量、湿度在尺度S-4能引起全部显著差异(表4),海拔则在尺度S-2,而土壤类型、植被指数、年均气温则需更小尺度才可以引起差异。在同一尺度下,各影响因素引起的空间变异也是不同的,如在尺度S-7,降水量、湿度引起的有机质和全氮含量差异显著比(差异显著对数/所有成对数)最大,年均气温、植被指数次之,海拔最小,而土壤类型则差异不显著。且随着尺度增大,有机质和全氮含量的差异显著比均由显著逐渐衰减,但不同的影响因素衰减速率不同,如降水量因素从尺度S-0到S-10,有机质含量差异显著比逐渐降低,由6/6降到4/6,衰减速率较慢,而海拔的差异显著比则由6/6降到1/6,衰减速率较快。

表4   不同尺度间的SOM、STN在不同影响因素下的显著性差异统计

Table 4  Statistical significance of SOM and STN at different scales and different levels of influencing factors

影响因素指标S-0S-1S-2S-3S-4S-5S-6S-7S-8S-9S-10
土壤类型有机质13/2112/2110/219/215/213/211/210/210/210/210/21
全氮8/218/217/216/215/212/21*2/210/21*0/210/210/21
植被指数有机质6/6**6/6**6/6***5/6***5/6***4/6***4/6***4/6***3/6***3/6***3/6***
全氮5/6**5/6**5/6**5/6**5/6***5/6***5/6***5/6***3/6***4/6***3/6***
年均气温有机质5/65/65/64/64/63/62/63/61/61/61/6
全氮3/63/63/62/63/62/60/60/60/60/60/6
降水量有机质6/6**6/6**6/6**6/6**5/6**5/6**5/6***5/6**4/6***4/6***4/6***
全氮6/6**6/6**6/6**6/6**6/6**5/6**5/6**4/6***4/6**4/6**3/6***
湿度有机质6/6**6/6**6/6**6/6**6/6**6/6**5/6**5/6**5/6**4/6**4/6**
全氮6/6**6/6**6/6**6/6**6/6**5/6**5/6**4/6**5/6**4/6**4/6**
海拔有机质6/66/66/64/64/63/63/62/62/62/61/6
全氮5/65/63/63/62/62/61/61/60/61/60/6

注:用上四分位、中位、下四分位3个节点将影响因素划分为4个水平;用独立样本Kruskal-Wallis非参数检验对各因素、不同水平下SOM、STN的数据集进行检验,其显著差异的对数为分子,所有成对数为分母;“***”表示强相关性,“**”表示中等相关性,其余表示无相关性。

新窗口打开| 下载CSV


综上所述,随着尺度增大,采样距离增大,数据集空间自相关性降低,变异系数变大,空间变异先增大后趋于平稳,但随机性变异逐渐减少,而结构性变异则先增加后降低,这主要是由于在小尺度时,大尺度的结构变异比较微弱又作为“随机变异”被忽视或降维扣除[8,27-28],在大尺度时,小尺度因素引起的结构特征被掩盖[2],所以随着尺度变大,随机变异逐渐减少。而大尺度因素随着尺度增大影响作用逐渐突显,结构变异逐渐增加,同时随着尺度的增大,点位间的空间相关性逐渐减弱,达到一定尺度后,大尺度的结构因素转换为相对的小尺度因素,其影响作用逐渐减弱,所以随着尺度变大,结构性变异先增大后减小。

另外,由于有机质和全氮固有性质和当地政策的不同,间接影响了其空间变异,如延安地区退耕还林还草空间分布不均,进入土壤各采样点位的有机质差异较大[12],而氮由于在土壤中转化、损失途径多,残留少,与自然成土过程中氮的空间分布相似[8],引起有机质的含量差异显著比均高于全氮,从而造成有机质具有较大的空间变异。

4 结论

变异系数、莫兰指数,半方差函数值和分形维数FD等空间分析方法的灵敏性较高,能从数据统计、空间集聚性以及变异结构等不同角度反映出有机质和全氮含量空间变异的随机性和结构性,三者结合能较好地反映空间变异的尺度效应特征。随着尺度增大,空间集聚性降低,有机质和全氮含量空间总变异先增大后趋于稳定,但随机性变异逐渐减少,结构性变异先增大后减少;相比大尺度而言,小尺度的随机变异占比较多,结构变异占比较少。

小尺度因素引起随机性变异,大尺度因素引起结构性变异,但不同结构影响因素对有机质和全氮含量的空间变异具有不同的区分度,高程的区分度最小,土壤类型、植被指数、年均气温、湿度等影响因素的区分度次之,降水量的区分度最大。各影响因素对有机质和全氮空间变异的影响具有尺度特征,随着尺度增大,小尺度因素引起的随机变异逐渐减少,而大尺度因素引起的结构性变异先增大后减弱,直至转换为相对的小尺度因素。

不同尺度上,影响因素对有机质和全氮的含量具有不同的相互协同机制,引起尺度间的随机变异和结构变异消长,造成各尺度空间总变异具有不同的结构组成,呈现出先减少后趋于稳定的变化趋势。

参考文献

齐雁冰, 常庆瑞, 刘梦云, 等.

县域农田土壤养分空间变异及合理样点数确定

[J]. 土壤通报, 2014, 45(3):556-561.

[本文引用: 2]

Qi Y B, Chang Q R, Liu M Y, et al.

County-scale spatial variability of soil nutrient distribution and determination of reasonable sampling density

[J]. Chinese Journal of Soil Science, 2014, 45(3):556-561.

[本文引用: 2]

张法升, 刘作新.

分形理论及其在土壤空间变异研究中的应用

[J]. 应用生态学报, 2011, 22(5):1351-1358.

[本文引用: 4]

Zhang F S, Liu Z X.

Fractal theory and its application in the analysis of soil spatial variability:A review

[J]. Chinese Journal of Applied Ecology, 2011, 22(5): 1351-1358.

[本文引用: 4]

Heuvelink GBM, Webster R.

Modelling soil variation:Past, present and future

[J]. Geoderma, 2001, 100: 269-301.

DOI:10.1016/S0016-7061(01)00025-8      URL     [本文引用: 2]

Jenny H. Factors of soil formation:A system of quantitative pedology[M]. New York: Dover Publications, 1994.

[本文引用: 1]

姜秋香, 付强, 王子龙.

空间变异理论在土壤特性分析中的应用研究进展

[J]. 水土保持研究, 2007, 14(4): 413-415.

[本文引用: 2]

Jiang Q X, Fu Q, Wang Z L.

Research progress of the spatial variability theory in application to soil characteristic analysis

[J]. Research of Soil and Water Conservation, 2007, 14(4): 413-415.

[本文引用: 2]

霍霄妮, 李红, 张微微, 等.

北京耕作土壤重金属多尺度空间结构

[J]. 农业工程学报, 2009, 25(3):223-229.

[本文引用: 5]

Huo X N, Li H, Zhang W W, et al.

Multi-S spatial structure of heavy metals in Beijing cultivated soils

[J]. Transactions of the CSAE, 2009, 25(3): 223-229.

[本文引用: 5]

潘瑜春, 刘巧芹, 阎波杰, 等.

采样尺度对土壤养分空间变异分析的影响

[J]. 土壤通报, 2010, 41(2):257-262.

[本文引用: 4]

Pan Y C, Liu Q Q, Yan B J, et al.

Effects of sampling S on soil nutrition spatial variability analysis

[J]. Chinese Journal of Soil Science, 2010, 41(2): 257-262.

[本文引用: 4]

雷咏雯, 危常州, 李俊华, 等.

不同尺度下土壤养分空间变异特征的研究

[J]. 土壤, 2004, 36(4):376-381.

[本文引用: 4]

Lei Y W, Wei C Z, Li J H, et al.

Characters of soil nutrient spatial variability in different S

[J]. Soil, 2004, 36(4): 376-381.

[本文引用: 4]

刘伟, 郜允兵, 周艳兵, 等.

农田土壤重金属空间变异多尺度分析——以北京顺义土壤Cd为例

[J]. 农业环境科学学报, 2019, 38(1):87-94.

[本文引用: 3]

Liu W, Gao Y B, Zhou Y B, et al.

Multi-S analysis of spatial variability of heavy metals in farmland soils: Case study of soil Cd in Shunyi District of Beijing,China

[J]. Journal of Agro-Environment Science, 2019, 38(1): 87-94.

[本文引用: 3]

郑袁明, 陈煌, 陈同斌, 等.

北京市土壤中Cr、Ni含量的空间结构与分布特征

[J]. 第四纪研究, 2003, 23(4):436-445.

[本文引用: 1]

Zheng Y M, Chen H, Chen T B, et al.

Spatialdistribution patterns of Cr and Ni in soils of beijing

[J]. Quaternary Sciences, 2003, 23(4): 436-445.

[本文引用: 1]

陈涛, 常庆瑞, 刘钊, 等.

耕地土壤有机质与全氮空间变异性对粒度的响应研究

[J]. 农业机械学报, 2013, 44(10):122-129.

[本文引用: 4]

Chen T, Chang Q R, Liu Z, et al.

Spatial variablility response of farmland soil organic matter and total nitrogen to sampling grain size

[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(10):122-129.

[本文引用: 4]

王鹏, 刘拓, 邱德明.

基于局部惩罚型变权的建设用地生态适宜性空间模糊评价——以陕西延安宝塔区为例

[J]. 西北地质, 2021, 54(1):232-241.

[本文引用: 4]

Wang P, Liu T, Qiu D M.

Spatial fuzzy assessment of ecological suitability for urban land based on local penalty variable weights:A case study of Baota district

[J]. Northwestern Geogloy, 2021, 54(1):232-241.

[本文引用: 4]

杨奇勇, 杨劲松, 刘广明.

土壤速效养分空间变异的尺度效应

[J]. 应用生态学报, 2011, 22(2):431-436.

[本文引用: 1]

Yang Q Y, Yang J S, Liu G M.

S-dependency of spatial variability of soil available nutrients

[J]. Chinese Journal of Applied Ecology, 2011, 22(2): 431-436.

[本文引用: 1]

Antonio P M.

Spatial variability patterns of phosphorus and potassium in no-tilled soils for two sampling scales

[J]. Soil Science Society of America Journal, 1996, 60(5): 1473-1481.

DOI:10.2136/sssaj1996.03615995006000050027x      URL     [本文引用: 1]

李小昱, 雷廷武, 王为.

农田土壤特性的空间变异性及分形特征

[J]. 干旱地区农业研究, 2000, 18(4): 61-65.

[本文引用: 4]

Li X Y, Lei T W, Wang W.

Spatial variablelity and fractal dimension of soil property in field

[J]. Agricultural Research in the Arid Areas, 2000, 18(4): 61-65.

[本文引用: 4]

沈思源.

土壤空间变异研究中地统计学的应用及其展望

[J]. 土壤学进展, 1989, 17(3):11-25.

[本文引用: 2]

Shen S Y.

Application and prospect of geostatistics in soil spatial variability research

[J]. Advances in Soil Science, 1989, 17(3): 11-25.

[本文引用: 2]

盛建东, 肖华, 武红旗, 等.

不同取样间距农田土壤全量养分空间变异特征研究

[J]. 土壤通报, 2006, 37(6):1062-1065.

[本文引用: 1]

Sheng J D, Xiao H, Wu H Q, et al.

Spatial variability of total nutrients in arable soil as affected by different sampling distances

[J]. Chinese Journal of Soil Science, 2006, 37(6) : 1062-1065.

[本文引用: 1]

李雅琦, 田均良, 刘普灵.

黄土高原土壤元素含量地域分异规律

[J]. 西北农业学报, 2000, 9(3):63-66.

[本文引用: 1]

Li Y Q, Tian J L, Liu P L.

A Study on laws of regional variance of soil element in loess plateau through trend surface analysis method

[J]. Acta Agriculturae Boreali-occidentalis Sinica, 2000, 9(3):63-66.

[本文引用: 1]

王鹏, 段星星, 赵禹, 等.

治沟造地新增耕地的土壤质量评价——延安宝塔区为例

[J]. 土地开发工程研究, 2019, 4(1):41-45.

[本文引用: 2]

Wang P, Duan X X, Zhao Y, et al.

The evaluation of soil nutrient status in newly reclaimed land from trench construction:Taking Baota district of Yan'an city as example

[J]. Land Development and Engineering Research, 2019, 4(1):41-45.

[本文引用: 2]

陈云坪, 王秀, 马伟, 等.

小麦多年产量空间变异与空间关联分析

[J]. 农业机械学报, 2010, 41(10):180-184.

[本文引用: 2]

Chen Y P, Wang X, Ma W, et al.

Spatial autocorrelation analysis of wheat yield over five years

[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(10): 180-184.

[本文引用: 2]

Burrough P A.

Multiscale sources of spatial variation in soil. I. The application of fractal concepts to nested levelsof soil variation

[J]. European Journal of Soil Science, 1983, 34: 577-597.

[本文引用: 3]

张忠启. 采样点布设与区域土壤有机碳变异性研究[M]. 北京: 科学出版社, 2019:110-128.

[本文引用: 1]

Zhang Z Q. Sampling site arrangement and regional soil organic carbon variability[M]. Beijing: Science Press, 2019:110-128.

[本文引用: 1]

Lei G, Shao M A.

The interpolation accuracy for seven soil properties at various sampling Ss on the Loess Plateau, China

[J]. Journal of Soils and Sediments, 2012, 12(2): 128-142.

DOI:10.1007/s11368-011-0438-0      URL     [本文引用: 1]

Daniels, Lee W.

The Nature and Properties of Soils, 15th Edition

[J]. Soil Science Society of America Journal, 2016, 80(5):1428.

DOI:10.2136/sssaj2016.0005br      URL     [本文引用: 1]

李元年. 基于熵理论的指标体系区分度测算与权重设计[D]. 南京: 南京航空航天大学, 2008.

[本文引用: 1]

Li Y N. Evaluation and weight design of index system based on entropy theory[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.

[本文引用: 1]

王鹏, 刘拓, 段星星, 等.

基于熵权的土壤养分地球化学多级模糊综合评判——以陕西省关中地区为例

[J]. 水土保持通报, 2019, 39(6):136-141.

[本文引用: 1]

Wang P, Liu T, Duan X X, et al.

Multi-stage fuzzy comprehensive evaluation of soil nutrient geochemistry based on entropy weight:Take Guanzhong region for example

[J]. Bulletin of Soil and Water Conservation, 2019, 39(6):136-141.

[本文引用: 1]

金继运, 白山路. 精准农业与土壤养分管理[M]. 北京: 中国大地出版社, 2001:5l-57.

[本文引用: 1]

Jin J Y, Bai S L. Precision agriculture and soil nutrient management[M]. Beijing: China Dadi Publishing House, 2001:5l-57.

[本文引用: 1]

王鹏, 刘拓.

延安市宝塔区土壤养分地球化学评价中的变权效果

[J]. 物探与化探, 2020, 44(4):847-854.

[本文引用: 1]

Wang P, Liu T.

Variational weight effect in the geochemical evaluation of soil nutrients in Baota District of Yan'an City

[J]. Geophysical and Geochemical Exploration, 2020, 44(4):847-854.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com