基于深度神经网络的重力异常反演

doi:10.11720/wtyht.2022.1341

基于深度神经网络的重力异常反演

王蓉^,, 熊杰^,, 刘倩, 薛瑞洁

长江大学电子信息学院,湖北荆州 434023

Inversion of gravity anomalies based on a deep neural network

WANG Rong^,, XIONG Jie^,, LIU Qian, XUE Rui-Jie

School of Electronic Information, Yangtze University, Jingzhou 434023,China

通讯作者: 熊杰(1975-),男,博士,副教授,CCF会员,主要研究方向为地球物理反演理论、人工智能。Email:xiongjie@yangtzeu.edu.cn

责任编辑: 王萌

收稿日期: 2021-06-17 修回日期: 2021-10-21

基金资助:

国家自然科学基金项目(61673006)
湖北省教育厅科学技术项目(B2016034)

Received: 2021-06-17 Revised: 2021-10-21

作者简介 About authors

王蓉(1995-),女,硕士,主要研究方向为地球物理反演理论、人工智能。Email: 201972322@yangtzeu.edu.cn

摘要

为解决传统线性反演方法容易陷入局部极小,计算效率低等问题,本文提出了一种基于深度学习的重力异常反演方法。该方法首先构造不同形状的二维密度模型,正演得到重力异常,组成数据集;然后用该数据集训练深度神经网络;最后将重力异常数据输入到训练好的深度神经网络,直接得到反演结果。实验结果表明,该方法能快速、准确地反演出地下异常体的位置和形态,且具有较好的泛化能力和抗噪声能力,可用于重力异常反演。

关键词： 深度神经网络; 重力异常; 反演

Abstract

Traditional linear inversion of gravity anomalies is liable to encounter local minima and suffer low computational efficiency. Given this, this paper proposed a deep learning-based inversion of gravity anomalies. Specifically, two-dimensional density models of various shapes were firstly established, and gravity anomalies were obtained through forward simulation using these models to form a dataset. Then, a deep neural network was trained using the dataset. Finally, gravity anomaly data were input into the deep neural network to directly yield inversion results. Experimental results show that the inversion method proposed in this study can determine the locations and shapes of underground anomalies quickly and accurately, with high generalization ability and anti-noise ability. Therefore, this method can be used for the inversion of gravity anomalies.

Keywords： deep neural network; gravity anomaly; inversion

PDF (2197KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王蓉, 熊杰, 刘倩, 薛瑞洁. 基于深度神经网络的重力异常反演[J]. 物探与化探, 2022, 46(2): 451-458 doi:10.11720/wtyht.2022.1341

WANG Rong, XIONG Jie, LIU Qian, XUE Rui-Jie. Inversion of gravity anomalies based on a deep neural network[J]. Geophysical and Geochemical Exploration, 2022, 46(2): 451-458 doi:10.11720/wtyht.2022.1341

0 引言

深度神经网络(DNN)目前是许多人工智能应用的基础^[1],由于 DNN 在语音识别^[2]和图像识别^[3]上的突破性应用,使用 DNN 的应用量有了爆炸性的增长。近年来,以深度神经网络为代表的深度学习技术,成为工业界及科学计算领域最有效的方法之一,在许多应用中实现了超过传统方法的效果,得到了广泛的应用^[4]。

物性反演是常见的重力异常反演方法,它主要是将包含特殊地质体的地下空间剖分成特定尺寸的网格单元,通常通过线性迭代方法求解。然而,线性迭代反演容易陷入局部极小值,计算耗时,并且数据量大时会占用大量的计算机内存^[5]的困境。随着地球物理反演方法的发展,非线性方法因其具有全局寻优的特点而受到广泛关注,模拟退火(SA)、遗传算法(GA)、早期神经网络(NN)、粒子群优化(PSO)、蚁群优(ACO)等非线性方法^{[6⇓⇓⇓-10]},已被广泛应用于地球物理反演。

深度神经网络的本质是通过构建具有许多隐藏层的网络结构来学习更复杂的函数映射关系。深度神经网络相较于传统的人工神经网络来说更为高级,有望解决传统的神经网络依然存在的泛化不足和欠拟合等问题。目前,全连接(FC, fully connected)是地球物理应用中常用的一种深度神经网络体系结构。此方法计算过程简单,学习能力强,泛化能力强,已成功地应用于地球物理反演。Zhang等^[11]通过训练FC网络估算地下地震相的分布进行了全波形反演;马国庆等^[12]提出通过FC网络实现场源位置反演;梁立锋等^[13]提出在混合深度学习反演弹性阻抗基础上,探讨超参数对网络性能的影响,为深度学习地震反演超参数选取提供依据;Wu等^[14]使用全卷积残差网络(FCRN)进行声阻抗反演,并通过转移学习方法改善了它们的实验结果;Hu等^[5]采用深度学习的方法对磁数据进行反演。此外,基于深度学习的方法还可以开发用于地震检测和定位,故障检测,天油气藏预测以及波形分类和识别等方面^{[15⇓⇓⇓-19]}。深度神经网络在上述领域得到了初步的应用,并为重力反演领域提供了新的思路^[20⇓-22]。

因此,本文提出基于全连接神经网络的重力异常反演方法。该方法将重力异常作为数据集,利用深度全连接网络来预测地下二维密度模型。

1 方法原理

1.1 全连接网络

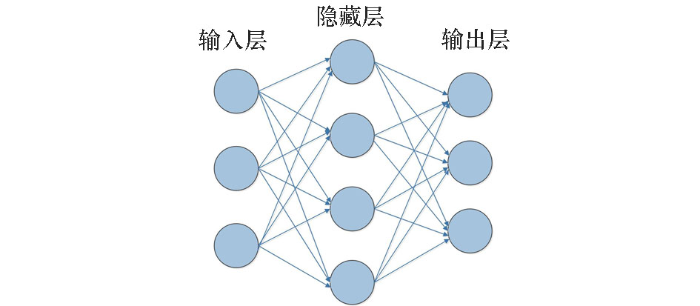
全连接网络的一般体系结构分为3种类型:输入层、隐藏层和输出层。输入层和输出层中的节点数分别由输入数据的大小和标签数决定,一个简单的三层全连接网络结构如下图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三层全连接网络结构

Fig.1 Three-layer deep fully connected neural network structure

图1是一个简单的三层全连接网络示意,全连接的含义是每一个节点会接受上一层所有节点的输出。网络的正向传播可以看作是从输入到输出的数据转换过程。在简单的三层深度全连接网络中,隐层又称为全连接层,隐层中每一个神经元都与前一层的所有神经元连接。一个隐层与其前一层之间的神经元权值的关系可表达为:

(1)

y = f (w^{T} x + b)

式中:x代表输入;y是输出;f是非线性激活函数;w是权重;b表示偏差值。

深度全连接网络结构擅于提取数据集中有用的信息,将输入数据转换为预期的输出。因此,为了达到学习的目的,并使网络的输出与实际值之间的误差最小,在学习过程中采用了反向传播算法。反向传播算法是训练中常用的算法,它使用损失函数来计算神经网络的梯度。均方误差(MSE)是深度全连接网络中常用的损失函数,可以定义为:

(2)

L = \frac{1}{2 N} \overset{N}{\sum_{i = 1}} (y_{i} - y_{i}^{'})^{2}

式中:y代表网络的输出;y'代表真实值;N表示样本数量。

深度全连接网络训练是一个不断优化的过程,因此,我们需要找到网络中权重和偏差的最佳参数值。权重和偏差的更新过程可以表示为:

(3)

\{\begin{array}{l} w' = w - η \frac{\partial L}{\partial w}, \\ b' = b - η \frac{\partial L}{\partial b} 。 \end{array}

式中:w和w'是在进入网络前后的权重;b和b'是网络迭代更新前后的偏差;η是学习速率,或称为步长,它用来控制网络的学习进度。通常,当学习率太低或是太高,网络训练都不会收敛,因此,需要找到最佳的学习率。参数更新过程完成之后,当达到最大迭代次数或训练出错时,可以停止网络训练。

1.2 基于深度全连接网络的重力异常反演

基于深度全连接网络的反演方法是一种非线性的地球物理反演方法,它的核心思想是用深度全连接网络建立从输入(地表观测数据)到输出(地下介质模型)之间的映射关系^[5]。地球物理反演问题是以正演计算为基础,已知从密度模型m到重力异常d的映射关系可以表示为矩阵方程,如式(4)所示:

(4)

d = G m

式中:d=(d₁,d₂,…,d_M)^T;m=(m₁,m₂,…,m_N)^T; M和N分别是观测点数量和网格单元的数量;G是M×N维核矩阵。

与传统方法不同,基于深度全连接网络的重力异常反演通过求解以下优化问题来实现^[5]:

(5)

\dot{Θ} = a r g m i n_{Θ} L (m, N e t (d, Θ))

其中:Θ表示网络中需要更新的权重和偏差;Net(·)深度全连接网络表示从观测数据d到预测密度模型m^pred之间的映射;L是MSE损失函数。上式的意义在于优化Θ,使得预测密度模型m^pred(Net(d, Θ))和真实密度模型m之间的误差最小。

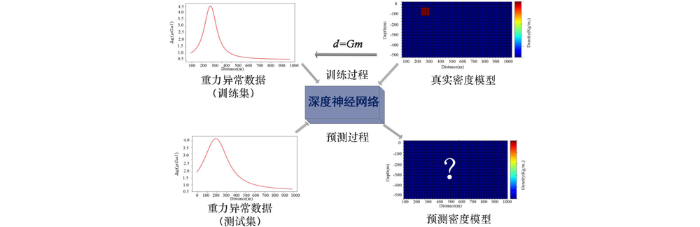
基于深度全连接网络的重力异常反演的示意图(图2)所示,首先,设计大量不同密度分布的模型样本,通过正演得到其对应的重力异常,构成训练数据集;然后利用该训练数据集训练深度全连接网络;最后,通过将重力异常输入到训练好的深度全连接网络,直接得到反演结果(地下介质密度模型)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于深度全连接网络的重力异常反演示意

Fig.2 Schematic diagram of gravity anomaly inversion based on deep fully connected network

通常,基于深度全连接网络的反演,在训练阶段会花费更多的时间,并且,时间开销与样本大小和网络结构有关系,但是一旦训练完毕,反演计算时间就可以基本忽略。

2 网络结构及L2正则化

2.1 深度全连接网络的建立与训练

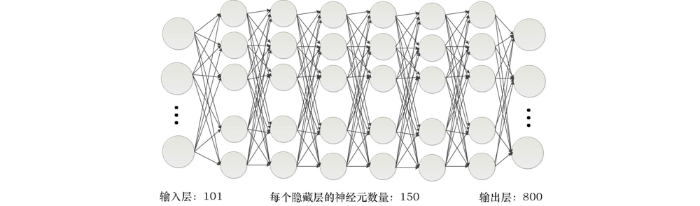
在本文中, 综合考虑到深度全连接网络的训练速度、网络结构以及重力异常d与密度模型m的关系,通过进行多次尝试并参考我们的训练和反演结果,设计了图3所示的网络结构。该深度全连接网络一共有6个隐藏层,每个隐藏层的神经元数量设置为150,输入层包含101个神经元,输出层包含800个神经元。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 深度全连接网络

Fig.3 Deep fully connected network

2.2 L2正则化

深度全连接网络中存在的一个普遍问题就是容易过拟合,表现为网络模型过于复杂,在训练集上预测误差很小,但在测试集上预测误差较大,泛化能力非常弱。为了防止过度拟合,需要使用L2正则化来改善网络。

L2正则化也称为权重衰减,是用于改善深度神经网络过度拟合的常用方法,L2正则化的本质是在原始损失函数的基础上添加参数,从而限制网络的学习能力。另外,为了使神经网络更全面地学习样本数据,我们将真实观测的异常数据d与预测的异常数据(d'=Gm')之间的损失项添加到原始损失函数中。总之,改进的损失函数表达式如下:

(6)

L' = L (m, m') + \frac{1}{2 N} \overset{N}{\sum_{i = 0}} (d_{i} - G m_{i}^{'})^{2} + \frac{λ}{2 n} \overset{n}{\sum_{i = 0}} w_{i}^{2}

式(6)的第一项是模型恢复程度,第二项是数据拟合程度,第三项为权重衰减正则化,它代表了网络中所有权值的平方和。式中, λ为正则化参数;n是训练集的大小。需要注意的是正则化项不包括偏置值。

3 模型试验与结果分析

3.1 数据集设置

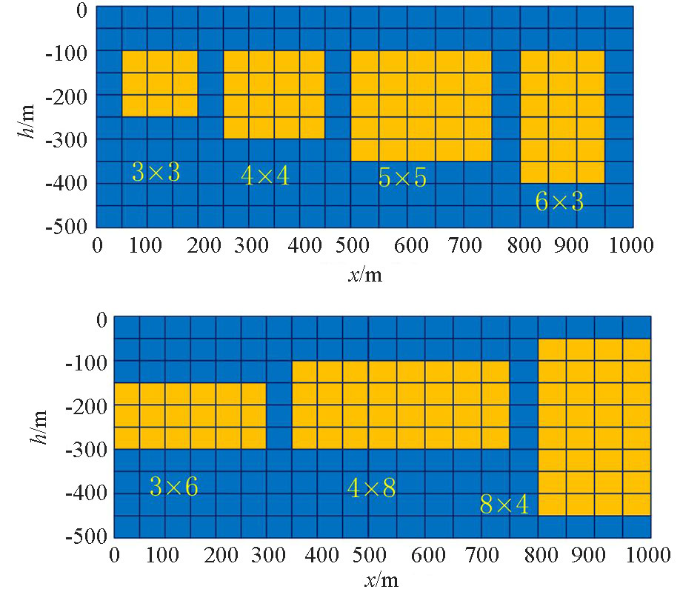
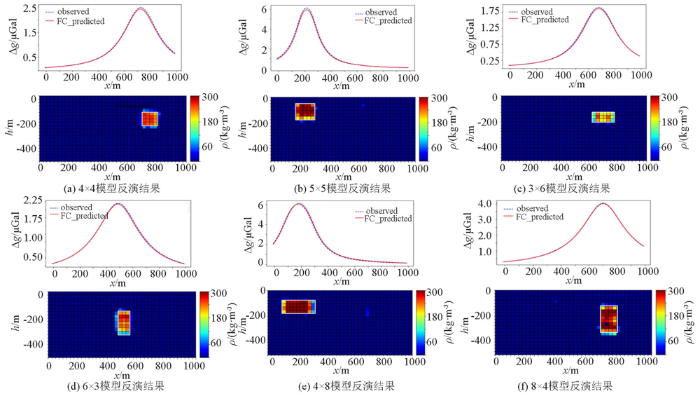
本文设计的观测系统如下:将地下空间划分为800个(20行×40列)矩形单元格,每个单元格大小为25 m×25 m,地面观测点设置为101个,观测点之间的间隔为10 m,设计了3×3(75 m×75 m)、4×4(100 m×100 m)、5×5(125 m×125 m)、3×6(75 m×150 m)、6×3(150 m×75 m)、4×8(100 m×200 m)、8×4(200 m×100 m)一共7个形状规则且单一的模型,如图4所示。考虑到密度到重力异常是线性关系,并且网络很容易学习这种简单的线性关系,因此,在本文中,仅仅为模型样本设置两个不同的密度值(200 kg/m³、300 kg/m³)。通过正演共生成了5 541组数据。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 7个单一模型示意

Fig.4 Schematic diagram of 7 single models

3.2 验证集测试

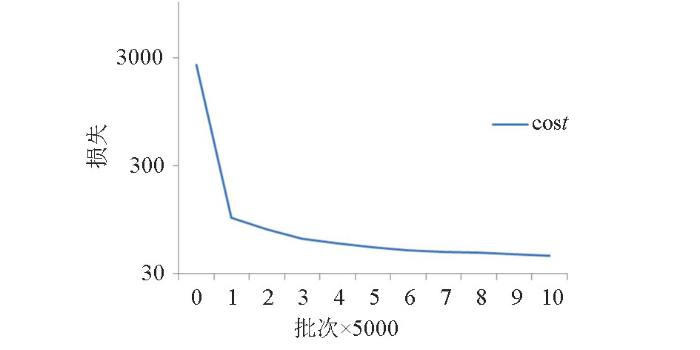
通常,训练集用于训练深度全连接网络的权重与偏差,而验证集用于验证训练后网络的准确性。在本文中,对于深度全连接网络,一共有5 541组数据样本,前80%作为训练集,后20%作为验证集。深度全连接网络反演训练及预测所需的时间分别为377 s和1.4 s。表1为深度全连接网络的反演参数设置。

表1 深度全连接网络反演参数设置

Table 1 Deep fully connected network inversion parameter settings

分类	参数设置	深度全连接网络
数据集	训练集	4432
	测试集	1109
网络设置	学习率	η=10^-4
	激活函数	ReLU
	优化器	Adam
	L2正则化	λ=0.01
训练过程	Epochs	50000
	Batch size	1000
目标函数	cost=a×cost1+b×cost2+c×cost3

新窗口打开| 下载CSV

从表1可以看出,目标函数对应式(6),将模型约束项cost1的权重a设为0.1,数据约束项cost2的权重b设为1,权重衰减项cost3的权重c设为1,cost1和cost2分别表示模型的恢复程度和重力异常的拟合程度;从表1可以看出,本方法的训练阶段虽有点耗时,但网络一旦构建好,实际的预测只需一秒多就完成。

本文使用表1的参数来训练深度全连接网络,总损失函数的变化情况如图5所示。从验证集中随机选取几组重力异常来测试训练后的深度神经网络的性能,图6展示了经过深度神经网络反演后获得的地下介质密度分布情况,并用白色线框显示真实模型的位置。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 损失变化曲线

Fig.5 Loss change curve

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 部分测试集样本的反演结果

Fig.6 Inversion results of part of the test set samples

图6中子图的上半部分表示重力异常曲线,蓝色的曲线表示实际的重力常值,红色的曲线表示经过深度全连接网络训练后的,预测出来的重力异常;每幅图的下半部分表示反演结果,白色线框表示真实的密度模型位置。从图6可以看出,预测出来的重力异常几乎与实际重力异常一致,说明深度全连接网络数据拟合的非常好;反演出的二维密度模型的形状和位置接近于真实模型,只是有些网格的密度值低于实际值(300 kg/m³),有些模型的周围存在少量的异常信息。

3.3 泛化能力测试

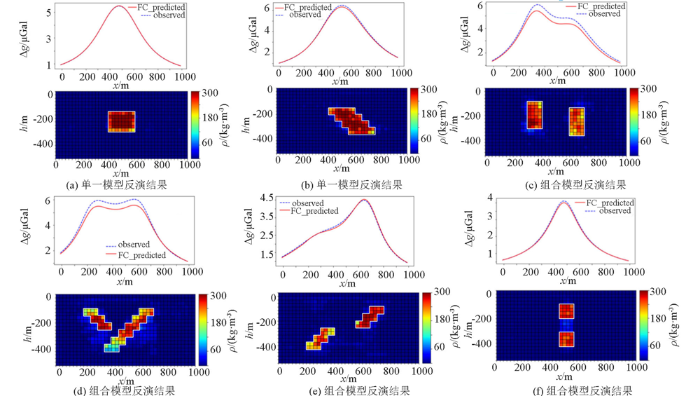
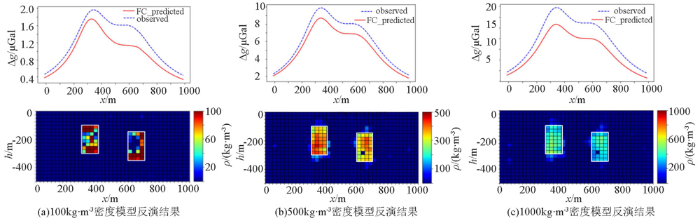
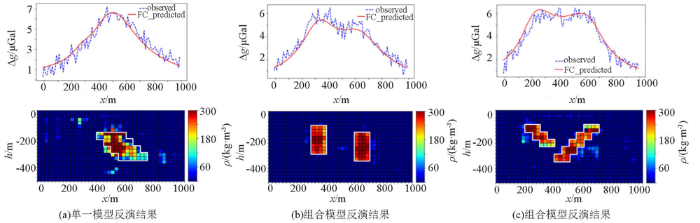
由于训练集和验证集都是从总样本中提取的,所以,训练集的反演结果只能评估网络的质量,而不能评估网络的泛化能力。为了评估该网络的泛化能力,本文设计了多个复杂模型,且该模型对应的重力异常数据都不参与网络训练,并根据不同的密度参数进行了两组实验。其中,实验1采用被学习过的密度参数的异常做反演,密度分别为200、300 kg/m³,实验2采用未被学习的其他密度参数的异常做反演,密度分别为100、500、1000 kg/m³。

实验1设计了6种较为复杂的模型(如图7中的白框模型),模型密度为200 kg/m³或300 kg/m³,这些模型对应的重力异常数据不参与训练网络,通过10次实验,求得平均数反演数据,最后的泛化能力测试结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 6种复杂模型样本的平均反演结果

Fig.7 Average Inversion results of six complex model samples

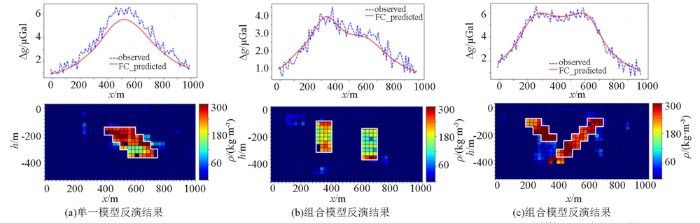
在图7a~b中,单一复杂模型的反演结果的位置、埋深、边界及位置几乎与真实模型一致;在图7c~e中,有些复杂的组合模型预测出来的重力异常略低于实际重力异常,反演出的二维密度模型的位置、埋深、边界及位置几乎与真实模型一致,但有些模型的密度低于实际密度值;在图7f中,组合垂直分离模型的反演结果,虽然中间有细微的连接,但还是具有较好的分辨率。从而说明深度全连接网路可以用来解决重力异常反演的问题,并且具有较好的泛化能力。

为了进一步测试本方法的泛化能力,实验2分别对未被学习的密度模型进行反演实验,反演时选取的密度参数分别为100、500、1 000 kg/m³,反演结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同密度参数得到的异常数据反演结果

Fig.8 Inversion results of abnormal data obtained with the same density parameters

从图8a实验结果可以看出,当模型密度为100 kg/m³时,能够反演出异常体的位置,但不能完全反演出异常体的形状;从图8b实验结果可以看出,当模型密度为500 kg/m³时,能准确地反演出异常体的位置和形状,数据拟合的也较好;从图8c实验结果可以看出,当模型密度为100 kg/m³时,能准确地反演出异常体的位置和形状,但密度值低于实际值,数据拟合也不好。从以上反演结果图可知,当模型密度与训练样本密度差距不大时,反演出的效果最好。

3.4 抗噪能力分析

已知在真实的环境中,重力异常数据通常受噪声等因素的影响。因此抗噪能力分析是评估网络质量的重要步骤。本文采用上节设计的3种复杂模型样本(如图9中的白框模型,这些模型重力异常数据不参与训练网络),同时对该数据分别加入5 dB和10 dB的高斯白噪声,反演结果如图9和图10所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 加入5 dB的高斯白噪声后的反演结果

Fig.9 Inversion result after adding 5 dB Gaussian white noise

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 加入10 dB的高斯白噪声后的反演结果

Fig.10 Inversion result after adding 10 dB Gaussian white noise

图9和图10上半部分的蓝色曲线表示加了5%和10%的实际重力异常值,红色曲线表示经过深度全连接网络训练后的,预测出来的重力异常;每幅图的下半部分表示反演结果,白色线框表示真实的密度模型位置。从图9、图10实验结果可以看出, 反演结果受噪声的影响较小, 虽然反演准确度有所下降, 但反演出异常体的形状和位置都接近于真实模型,说明基于深度全连接网路的重力异常反演,具有较好的抗噪声能力。

4 结论

本文提出了基于深度全连接神经网络的重力异常反演方法,该方法首先构造不同形状的二维密度模型,通过正演得到重力异常观测值,组成训练集,然后,用该训练集来训练深度神经网络,最后直接输入重力异常观测值到训练好的深度全连接网络,得到预测的二维密度模型。实验结果表明,该方法可以快速准确反演出异常体的位置和密度,具有较好的泛化能力和抗噪声能力,能用于重力异常反演问题。

深度全连接网络在深度神经网络中属于比较简单的网路,下一步工作将围绕如何设计更深、更复杂的网络结构以改进反演效果,并应用于三维重力反演等方面。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

C Y

, Bengio

, Hinton

Deep learning

[J]. Nature, 2015, 521(7553): 436-444.

DOI:10.1038/nature14539 URL [本文引用: 1]

[2]

吴渤

. 基于深度神经网络的语音去混响方法研究[D]. 西安: 西安电子科技大学, 2018.