E-mail Alert Rss
 

物探与化探, 2022, 46(2): 275-284 doi: 10.11720/wtyht.2022.2446

综述

基于反馈迭代模型的多次波压制方法综述

贺紫林, 李振春, 李志娜, 徐夷鹏

中国石油大学(华东) 地球科学与技术学院,山东 青岛 266580

A review of multiple suppression methods based on feedback iteration model

HE Zi-Lin, LI Zhen-Chun, LI Zhi-Na, XU Yi-Peng

School of Geosciences,China University of Petroleum(East China),Qingdao 266580,China

通讯作者: 李志娜(1986-),女,博士,副教授,长期从事地震波传播与成像方法研究工作。

责任编辑: 叶佩

收稿日期: 2020-10-12   修回日期: 2021-11-2  

基金资助: 中石油重大科技专项(ZD2019-183-003)
国家自然科学基金项目(42074133)
国家自然科学基金项目(41974145)
中央高校基本科研业务费专项资金项目(18CX02009A)
中央高校基本科研业务费专项资金项目(20CX02105A))
中国石化胜利物探研究院横向课题(30200020-20-ZC0607-0020)
国家科技重大专项(2016ZX05026-002-002)

Received: 2020-10-12   Revised: 2021-11-2  

作者简介 About authors

贺紫林(1995-),女,现为中国石油大学(华东)在读研究生,主要从事多次波压制方面的研究工作。

摘要

在油气勘探中,多次波通常被视为影响地震数据处理和解释结果准确性的相干噪声,因此,多次波压制方法研究一直是地球物理勘探领域中的重要研究方向。鉴于自由表面多次波是地震勘探尤其是海上地震勘探资料中最为发育的多次波类型,因此,对自由表面多次波压制方法的研究是十分必要的。目前国内外精度较高且应用广泛的自由表面多次波压制方法即为基于波动方程的反馈迭代法,该方法以地震原始数据为预测因子,不需要其他先验条件,可以在数据驱动下实现高精度的自由表面多次波压制。在该方法理论基础上,近年来发展了一系列更为先进的方法技术。本文首先简要介绍了反馈迭代法的理论基础——反馈迭代模型;然后阐述了基于反馈迭代模型发展的SRME、反数据域法、EPSI、CL-SRME四种方法压制自由表面多次波的机理;最后对比了四种方法各自的优缺点,展望了基于反馈迭代模型的多次波压制方法的研究前景。

关键词： 自由表面多次波; SRME; 反数据域; EPSI; CL-SRME

Abstract

In oil and gas exploration,multiples are usually regarded as the coherent noise that affects the processing and interpretation accuracy of seismic data.Therefore,the study of multiple suppression methods has always been an important research direction in the field of geophysical prospecting.Given that the surface-related multiples are the most developed multiples in seismic exploration,especially in marine seismic exploration,it is necessary to conduct a deep study on the suppression methods of surface-related multiples.At present,the surface-related multiple suppression method that enjoys high accuracy and is widely applied at home and abroad is the feedback iteration method based on the wave equation.This method takes the original seismic data as the predictive factor and requires no other prior conditions and allows for high-precision suppression of surface-related multiples driven by data.A series of more advanced methods have been developed based on the theory of this method in recent years.This paper briefly introduces the theoretical basis of the feedback iteration method(i.e.,the feedback iteration model) firstly and then describes the surface-related multiple suppression mechanisms of the four methods developed based on the feedback iterative model, namely SRME,the inverse data domain method,EPSI,and Cl-SRME.Finally,it compares the advantages and disadvantages of these four methods and proposes the research prospects of multiple suppression methods based on the feedback iteration model.

Keywords： surface-related multiple; SRME; inverse data domain; EPSI; CL-SRME

PDF (2917KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

贺紫林, 李振春, 李志娜, 徐夷鹏. 基于反馈迭代模型的多次波压制方法综述[J]. 物探与化探, 2022, 46(2): 275-284 doi:10.11720/wtyht.2022.2446

HE Zi-Lin, LI Zhen-Chun, LI Zhi-Na, XU Yi-Peng. A review of multiple suppression methods based on feedback iteration model[J]. Geophysical and Geochemical Exploration, 2022, 46(2): 275-284 doi:10.11720/wtyht.2022.2446

0 引言

多次波压制问题一直是石油勘探领域中非常重要的一个课题,也是地震数据处理过程中的重点和难点之一。随着勘探工作的深入和研究目标的复杂化,地下构造的成像精度要求也越来越高。多次波的存在会降低地震资料的信噪比,在地震成像过程中产生假象,影响成像结果的可靠性和真实性。而成像结果的质量直接关系着地震资料解释结果的准确性,进一步影响着井位部署和油气勘探的成功率[1]。

随着油气勘探的进步、计算能力的不断提升,多次波压制方法也在不断发展。目前,多次波的压制方法大致可分为两类。一类是基于一次波和多次波之间周期性差异和动校正时差差异的滤波方法,简称为滤波法,如f-k滤波、Radon变换、预测反褶积等。此类方法简单,但是在地下复杂介质中适应性差,对多次波压制效果不理想[2]。一类是基于波动方程的预测减去方法,这种方法通过波动方程模拟实际波场或反演地震数据来预测多次波,然后将其从原始地震数据中减去,简称预测减去法,其中包括反馈迭代法、恒定内插法、波场外推法、逆散射级数法等。这类方法克服了滤波法的缺点,对复杂地下构造具有很好的适应性。根据产生多次波最浅的下行反射边界,多次波被分为两类:自由表面多次波(surface-related multiple)和层间多次波(internal multiple),随之出现了自由表面多次波衰减和层间多次波衰减的概念。自由表面多次波发育广泛,在海洋地震勘探资料中尤为明显,它的存在影响着地震资料一次波识别的准确性,从而使处理的地震剖面存在假象,得到错误的解释结果。因此,在地震数据处理过程中自由表面多次波压制工作是必不可少的。鉴于波动方程理论的高精度特性,目前,采用预测减去方法中基于反馈迭代模型理论的一类方法实现对自由表面多次波的压制是一个很好的选择。

1 反馈迭代模型

20世纪60年代,Anstey和Newman提出有效波可以通过地震道信号的褶积转化为多次波,这为之后的反馈迭代法奠定了理论基础。Riley等[3]于1976年提出了二维垂直入射时的自由表面多次波模拟算法,但未找到合适的反演方案。Kennett[4]于1979年实现了一维自由表面多次波的模拟和反演,但由于该算法对地下介质和资料采集方式过多的简化和假设,在实际应用中效果并不是很成功。

20世纪80年代,Berkhout[5]提出了自由表面多次波的反馈理论框架,将震源和滤波器的特性考虑其中,突破了对介质和波入射方向的要求,并对自由表面多次波达到了较好的反演效果,奠定了基于反馈迭代模型的多次波压制方法的数学物理基础。

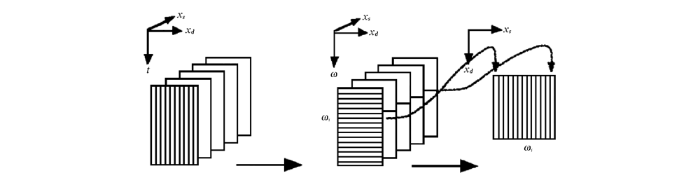
反馈迭代模型是在单频分量矩阵之间的计算上建立的,假设将观测到的地震数据记为p(xr,xs,t),将地震数据转换到频率域变为p(xr,xs,ω),提取单频分量的地震数据矩阵记为P(如图1)[6]。一次波(即无自由表层多次波的期望数据)单频分量矩阵记为P0,自由表面多次波单频分量矩阵记为M。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   提取单频分量过程

Fig.1   Extraction process of single frequency component matrix


将地震波在地层中的传播看作是大地滤波过程,若无自由表面,一次波可表示为:P0=X0S(如图2a)[7-8]。而自由表面的存在使得这个滤波器变成一个带反馈的滤波器(如图2b)[7-8],其反馈模型表达式总结为:

P=X0(S+RP)=X0S+X0RP=P0+M

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   反馈模型示意

a—不含自由表面多次波;b—含自由表面多次波

Fig.2   Feedback model

a—forward model of seismic data without surface-related multiple;b—forward model of seismic data with surface-related multiple


其中P0=X0SM=X0RP,X0为一次波脉冲响应,S为震源矩阵(地震子波函数),R为表面反射系数矩阵。

式(1)反馈模型的提出,在没有过多简化的情况下提供了一种新的自由表面多次波压制思路,人们在此理论上,首先发展出了SRME(surface-related multiple elimination)自由表面多次波压制方法,并在其基础上,扬长避短,在发现问题、解决问题的过程中不断提出更加优化的自由表面多次波压制方法。下面将对基于反馈迭代模型的四种常用方法进行简要的介绍。

2 基于反馈迭代模型的多次波压制方法

2.1 SRME方法

SRME是最经典的反馈迭代方法,Verschuur[9]于1991年在反馈迭代模型理论上通过引入一次波能量最小假设实现了多次波的自适应相减,很大程度推动了SRME的发展。Berkhout和Verschuur[7-8] 在1997年提出了迭代SRME方法,将自由表面算子的估计从一个非线性问题转化为线性问题,并通过实际应用说明收敛速度比较快,几次迭代就可以较好地实现自由表面多次波压制。

该方法是由式(1)入手,推得M=P0S-1RP=P0AP,于是可概括为:

P0(1)=P,P0(i+1)=P-P0(i)A˙P。

式中:A=S-1R为自由表面算子;A˙表示为A的估计值。为了简化计算,假设A是不依赖角度的,即忽略了震源和检波器的方向特性,也就是说自由表面算子A为一个对角矩阵,可表示为A(ω)=A˙(ω)I。虽然这一基本假设在实际中不一定满足,但已经在许多实际数据中成功地执行并证明了其可行性。在之后介绍的EPSI和CL-SRME方法中,此假设依然沿用。而对A的求取是在时间域通过最小二乘滤波实现的:

E=∑xr,xs,t[p(xr,xs,t)-a(t)·m(xr,xs,t)]2。　

式中:m(xr,xs,t)为时间域的自由表面多次波;a(t)为时间域的自由表面算子。在实际生产中,为使预测的多次波更接近实际多次波,可以将单炮或者单接收点道集应用最小二乘滤波对a更准确地求取,并且预测因子a的长度在一定范围内,多次波的预测会随着因子长度的增大而更为准确,但当超过此范围时不仅对预测结果影响不大,反而会增加计算量。因此,为了在最少的计算量下得到令人满意的自由表面多次波压制效果,多次波预测过程中需要选取合适的预测因子长度。一次波能量最小假设的引入虽然实现了多次波的自适应相减,但在一次波和多次波能量存在干涉时,此假设并不成立,从而会造成一次波能量的损伤。

SRME方法包括两部分,一部分是自由表面多次波的预测,另一部分是把预测出的自由表面多次波有效地从原始数据中减去。虽然预测的多次波在传播路径上做到了与实际的匹配,但在波的相位、时间、振幅等方面缺少充分的考虑,预测得到的多次波与实际的多次波相比具有一定差异,从地震资料中直接减去预测的多次波可能会得到错误的一次波信息,所以需要对预测得到的多次波与原始数据先进行匹配再进行相减。

在长期的研究进程中,国内外学者们提出了不同的匹配相减方法,Verschuur等[6]于1992年提出频率域最小能量滤波方法来消除自由表面多次波,并在1997年[7-8]提出了时间域单道维纳滤波方法。为达到更好的匹配相减结果,Monk[10]在1993年提出了伪多道维纳滤波。1999年Spitz等[11]提出了模式匹配滤波法。2003年,Guitton[12]提出了预测误差滤波,同年,Wang[13]对常规匹配方法进行了总结,并在此基础上提出了扩展伪多道维纳滤波,将匹配滤波器的约束由二维扩展到了三维。2004年陆文凯等[14]提出了基于独立变量分析方法,使用高阶能量统计函数来进行多次波的匹配相减,得到较好的效果。

之后许多学者进一步发展了SRME,Dedem和Verschuu[15-18]将SRME发展到了三维数据处理中,并在2005年提出将稀疏反演与三维SRME相结合。Anatoly等[19]于2006年通过共偏移距道集的DMO和反DMO操作进行数据重建,实现了三维SRME多次波压制。石颖等[20]在2013年提出全三维多次波预测方法,通过GPU并行的方式加速,在精度和速度上有了明显提升。井洪亮等[21]于2015年在GPU并行下实现基于L1、L2范数联合的SRME自适应相减,克服了L2范数的条件限制,也降低了L1范数的计算成本。

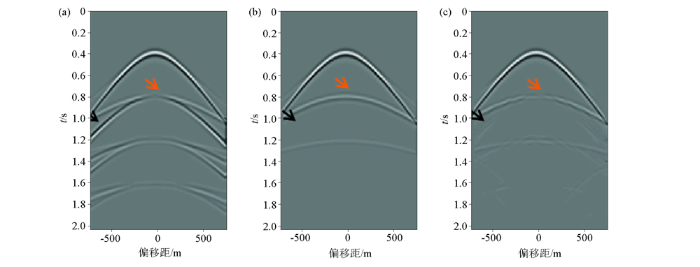
图3展示了SRME方法对三层水平层状模型正演数据的自由表面多次波压制结果[22]。由图3c可见,SRME在一定程度上压制了自由表面多次波能量,但仍存在明显的能量残余(如黑色箭头所示),并在一次波与多次波能量干涉处,存在一次波能量损失的情况(如橙色箭头所示)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   某炮数据SRME方法对自由表面多次波的压制结果

a—原始单炮数据;b—真实一次波;c—多次波压制结果

Fig.3   Suppression results of surface-related multiples of a shot record by SRME method

a—original shot record;b—real primaries;c—result of surface-related multiple suppression


SRME方法理论简单,只需要通过地震记录的褶积即可预测自由表面多次波,不需要额外的先验信息,可在较少的迭代次数下得到较好的压制结果。但在实际资料处理中,预测的多次波信息并非十分准确,在匹配相减后仍会有部分多次波能量残余存在。且在一次波和多次波干涉时,不再成立的一次波能量最小的前提假设会造成有效信号的损伤。虽然人们提出不少的匹配方法,但这些方法只降低了对一次波能量的损伤程度,未从根本上解决此问题。

2.2 反数据域方法

SRME方法中一次波能量最小的前提假设从方法上导致了它的局限性,而反数据域方法的提出,提供了一种避免该假设的多次波压制思路,以相同的理论基础、不同的推导方式解决了SRME存在的问题。Berkhout[23]在2006年将SRME理论发展到了反数据域, 从而避免自适应相减的这一过程。首先通过式(1)得到地震数据P显式表达式:

P=(I-X0R)-1(X0S)

对式(4)两边求逆,转换到反数据域:

P-1=(X0S)-1(I-X0R)=(X0S)-1-S-1R。

由式(1)、式(2)可知P0=X0S,A=S-1R,则原始地震记录P的逆为:

P-1=P0-1-A。

通过将地震数据转化到反数据域,观测到的地震记录P的逆被分解为两部分:一次波P0的逆和自由表面算子A。只需将反数据域中自由表面算子的成分去除,即可得到只关于一次波的信息。一次波数据P0在正数据域具有走时信息,在反数据域(P0-1)则位于负时间内,而自由表面算子A与时间无关,在反数据域是一个位于零时间和零时间附近的聚焦点。通过在Radon域将反数据域零时间左右的表面算子简单切除后,再将结果转换回正数据域,就可达到自由表面多次波压制的目的,避免了自适应相减过程,但需要注意的是对反数据域零时间周围信息的切除不精确也可能会导致一次波能量一定程度上的损失。

之后,许多学者对反数据域方法进行了扩展,Berkhout[24]于2006年在反数据域多次波压制过程中加入了反褶积处理方法。基于波动方程的数据驱动算法虽然在海洋地震多次波压制中相当有效,但在陆地数据中应用时需要特殊的预处理,Kelaims[25]在2006年实现了反数据域中陆地表面多次波的压制。Luo等[26]在2007年将反数据域方法发展到了层间多次波的压制上,给出了一维实例。Berkhout等[27]在2007年提出了一种利用反数据空间进行时移地震处理的新方法。同年,Berkhout等[28]实现了反数据域二维实际数据的层间多次波压制方法,并给出实例。马继涛等[29]在2009年介绍了两种矩阵求逆的方法,并给出了在二维情况下反数据域处理的实例。同年,马继涛等[30-31]结合平面波域多次波产生机理,实现了平面波域反数据处理压制自由表面多次波方法,在保证一次波能量不受损害的同时,更有效地达到了压制自由表面多次波的目的。

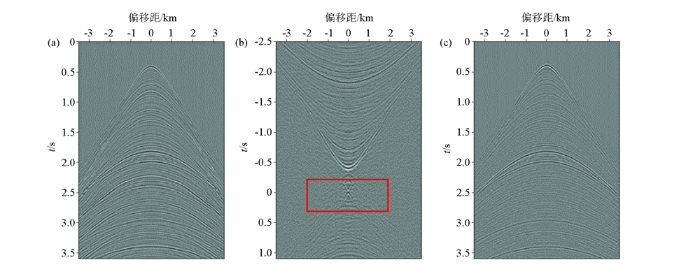
图4展示了反数据域法对比较复杂的水平层状模型正演数据的自由表面多次波压制结果[24]。由图4b可以看到在反数据域中自由表面算子聚焦在零时间处(如红框所示),通过线性Radon变换,将此聚焦点转换为τ=0这条直线,然后通过简单切除直线τ=0上的数据达到去除自由表面算子信息。再通过转换到正数据域后(如图4c)可以非常直观地看到自由表面多次波得到有效压制。

与正数据域中的表达公式相比,反数据域公式更加简单明了。反数据域方式算法简单,不需要大量的矩阵相乘运算,具有较大的计算速度优势,该方法利用了一次波和多次波在反数据域的可分离性,通过简单的切除操作就达到了自由表面多次波压制的目的,避免了自适应相减过程,解决了SRME在预测相减时对一次波能量的损伤问题。但由于需要做矩阵求逆运算,求逆过程容易引入噪声影响结果,因此需要选取合适的矩阵求逆方法[30]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   某炮数据反数据域法对自由表面多次波的压制结果

a—原始单炮数据;b—反数据域的地震炮记录;c—反数据域法多次波压制结果

Fig.4   Suppression result of surface-related multiple of a shot record in inverse data domain

a—original shot record;b—seismic shot record in inverse data domain;c—result of multiple suppression in inverse data domain


2.3 EPSI方法

为了更准确地得到一次波信息,寻找一种既能避免一次波能量最小假设, 又无求逆过程的自由表面多次波压制方法是很有必要的,于是EPSI方法顺势而生。2009年,Van Groenestijn等[32]提出了稀疏反演一次波估计方法(EPSI),将SRME中的一次波能量最小假设改变为使估计的一次波和多次波数据之和不断逼近地震原始数据的目的,即将地震数据和估计的一次波及多次波差值的能量作为目标函数J,使其最小化。

J=∑ωJω=∑ω‖P-(X˙0S˙+X˙0RP)‖2→min

式中,X˙0和S˙表示为一次波响应X0和震源子波函数S的估计值。假设所有反射系数R=-I,采用一阶泰勒展开的下降方法,求得一次波响应X0和震源子波函数S的最速下降方向:

ΔX0=(P-X˙0S˙+X˙0P)(S˙-P)HΔS=X˙H0(P-X˙0S˙+X˙0P)

式中:ΔX0和ΔS表示为一次波响应X0和震源子波函数S的梯度值;H表示复共轭转置运算。根据X0和S的梯度值得到X0和S的更新值:

X˙0(i+1)=X˙0(i)+α(i)ΔX0(i),S˙(i+1)=S˙(i)+α(i)ΔS(i)。

其中,α和β为通过ΔX0和ΔS对应搜索步长,求取公式如下:

α=∑ω(ΔVH1V)∑ω(ΔVH1V1)β=∑ω(ΔVH2V1/2)∑ω(ΔVH2V2)

其中,

V=P-X˙0S˙+X˙0P,ΔV1=ΔX0S˙-ΔX0P,V1/2=P-X˙0S˙+X˙0P,ΔV2=ΔX0ΔS˙。

为约束X0的反演过程,在时间域将稀疏性引入X0的反演过程中,从而加速目标函数的收敛。通过上式(8)~(10)可计算得到一次波响应X0和震源子波函数S的估计值,然后通过两者频率域相乘(或时间域褶积)得到一次波数据,若不满足要求,则继续迭代反演。可以看出对X0和S的估计值都对一次波估计值的准确度具有直接影响,反演过程中的多参数是影响EPSI方法速度与精度的重要因素。

随后,经过一系列改进,Van Groenestijn和Verschuur[33]在2010年将其发展到了被动源地震中,并实现了海底OBC数据EPSI一次波估计[34-39]。刘国昌等[40]在2013年实现了海底OBS数据EPSI一次波估计。Lin等[41]在2013年提出了L1范数下的EPSI一次波反演方法,提高了多次波压制结果的精度。为了提高多次波去除的准确性和效率,Lopez等[42]在2012年结合SRME和EPSI方法各自的优点,提出了一种SRME和EPSI联合的多次波压制方法。2013年,Ypma等[43]在此基础上扩展到了广义的EPSI方法,对海洋实际数据层间多次波进行了有效压制;Angarita等[44]在聚焦变换域实现了EPSI方法,重建了大范围缺失的地震数据;Feng等[45]提出L1范数约束下三维曲波变换稀疏反演一次波估计方法。程浩等[46]在2015年结合范数约束的准确性和优越性,提出了L1约束被动源数据稀疏反演一次波估计方法。

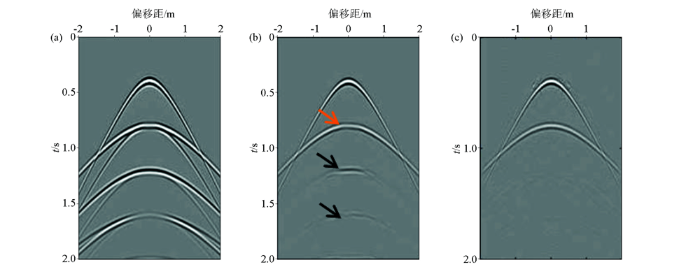
图5展示了EPSI方法对双层水平层状模型正演数据的一次波估计结果,并与SRME多次波压制结果进行对比[47]。EPSI对一次波的估计是通过X0和S进行褶积得到的,因此需要先对上述两者进行反演,再通过褶积得到估计的一次波信息(图5c),通过图5b~c 对比,可以看到,SRME方法在一次波和多次波具有能量干涉处(如橘色箭头所示)会产生一次波能量的损失,并且在局部地方存在明显的多次波能量残余(如黑色箭头所示)。而EPSI方法通过反演的方法成功避免了上述问题,比较准确地反演出了一次波能量。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   某炮数据EPSI方法对自由表面多次波的压制结果

a—原始单炮数据;b—SRME多次波压制结果;c—EPSI压制结果

Fig.5   Suppression results of surface-related multiples of a shot record by EPSI method

a—original shot record;b—result of surface-related multiple suppression by SRME;c—result of surface-related multiple suppression by EPSI


EPSI通过一个波形反演替换了SRME的预测和相减,一次波被直接反演得到,克服了SRME一次波能量损伤问题和反数据域的求逆过程。但是由于EPSI一次波脉冲响应的稀疏性假设,在存在波散等情况的复杂地下构造下无法选取准确的地下一次波响应初值,导致了不能得到令人满意的一次波估计效果[48]。并且EPSI需要额外的调优因子和较高的迭代次数,大大地增加了方法的计算量。

2.4 CL-SRME方法

SRME和EPSI各有优缺点,于是一种结合两种方法优势,避免双方劣势的自由表面多次波压制新方法被提出。Lopez等在2014年[22]提出了CL-SRME(Closed-loop SRME)方法,它和EPSI相似,也是通过波形反演的方式替代了SRME的预测相减,将传统的多次波预测方法变成了闭合循环的一次波反演方法。

为使估计的一次波及多次波之和尽可能接近地震记录,通过式(2)建立目标函数:

J=∑ωJω=∑ω‖P-P˙0(I+A˙P)‖2→min　

式中,P˙0表示一次波P0估计值。类似EPSI,采用一阶泰勒展开的下降方法,求得一次波P0的最速下降方向:

ΔP0=[P-P˙0(I+A˙P)](I+A˙P)H。

通过梯度值ΔP0对一次波P0进行第i次迭代数据更新:

P˙0(i+1)=P˙0(i)+αΔP0(i)

其中α为搜索步长,公式如下:

α=∑ωRe[Tr(VHK)]∑ωTr(KHK)

其中,

V=P-P˙0(I+A˙P)K=ΔP0(I+A˙P)

式中:Re表示取实部运算;Tr表示求矩阵的迹,即求矩阵主对角线数据之和。表面算子A与SRME中的假设和计算相同。可以看到,CL-SRME是直接求取一次波的梯度和步长,对一次波信息不断更新,直至符合要求。也正由于该方法是直接对一次波数据进行操作的,所以与EPSI方法相比CL-SRME方法对一次波反演更准确且更稳定。

之后,Lopez等[49-50]在2015年将CL-SRME方法发展到了聚焦域,完成了部分数据缺失的地震记录的重构和一次波估计。Lopez等[51]在2015年将聚焦域CL-SRME发展到三维。Vrolijk等[52]在2016年将CL-SRME用于鬼波的压制。Wang等[53]于2017年提出了三维L1范数下稀疏约束反演CL-SRME方法。Vrolijk等[54]在同年实现了CL-SRME方法对鬼波和多次波的一体化压制。王铁兴[48]在2020年提出在被动源数据中的三维稀疏约束CL-SRME一次波反演方法和混采数据CL-SRME一次波反演方法。

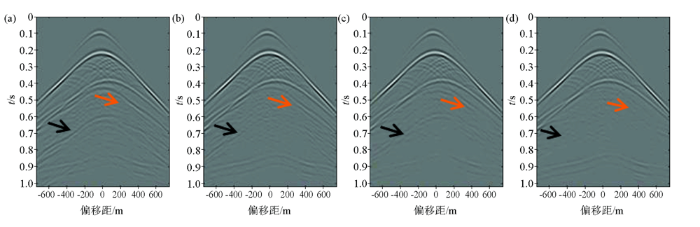
图6展示了CL-SRME方法对盐丘模型正演数据的一次波估计结果,并与SRME、EPSI两种方法对多次波压制结果进行对比[22]。可以看出,3种方法在不同程度上对自由表面多次波具有压制效果,通过图6b~d的比较可见,CL-SRME方法估计的一次波信息明显更为准确,更加全面(如橙色箭头所示),多次波能量的泄露也是最小的(如黑色箭头所示)。对于复杂构造,CL-SRME方法的适应性相比较EPSI来说更强。因此,CL-SRME方法是目前看来比较具有优势的自由表面多次波压制方法。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   某炮数据CL-SRME方法对自由表面多次波压制的结果

a—原始单炮数据;b—SRME多次波压制结果;c—EPSI多次波压制结果;d—CL-SRME多次波压制结果

Fig.6   Suppression results of surface-related multiples of a shot record by CL-SRME method

a—original shot record;b—result of surface-related multiple suppression by SRME;c—result of surface-related multiple suppression by EPSI;d—result of surface-related multiple suppression by CL-SRME


CL-SRME一次波估计方法避免了SRME的一次波能量损伤和EPSI稀疏性问题,也不需要逆计算,并具有较少的调优因子,只需不断更新自由表面算子A就可以达到一次波估计的效果。且迭代次数较少,在稳定性和准确性上比EPSI都有所提高。

2.5 SRME、反数据域法、EPSI、CL-SRME方法对比

本文介绍了反馈迭代模型和在此基础上发展的4种常用自由表面多次波压制方法的原理及研究进展,通过模型示例(表1)展示了4种方法压制自由表面多次波的效果,也直观地看出了每种方法的优缺点。4种方法以地震数据为预算因子实现了对自由表面多次波的压制,不需要额外的先验条件,但都需要全波场信息,对观测系统和观测数据要求比较严格;SRME和反数据域方法理论简单,但SRME在一次波与多次波具有能量干涉时,匹配相减会对一次波能量产生损伤,因此,对于如何做到更准确的匹配相减是SRME的发展方向;反数据域法的求逆运算容易引入噪声,寻找合适的求逆方法则是反数据域法的重点研究内容;EPSI避免了上述两种方法存在的问题,但由于稀疏性的引入,对复杂构造的适应性不强,并且需要较多的调优参数和较高的迭代次数;CL-SRME方法则避免了前3种方法的问题,具有较好的稳定性和准确性。但由于EPSI和CL-SRME是基于波形反演的思路,其计算成本要高于SRME和反数据域法。因此,如何提高计算精度与计算效率是EPSI和CL-SRME的研究重点。

表1   基于反馈模型多次波压制方法优缺点

Table 1  The advantages and disadvantages of multiple suppression methods based on feedback model

SRME反数据域法EPSICL-SRME
优
点		1.方法简单1.方法简单
2.避免自适应相减造成的一次波损伤
3.无大量矩阵相乘计算		1.无自适应相减过程
2.无求逆计算		1.无自适应相减过程
2.无求逆计算
3.有较少的调优参数
4.对复杂构造适应性强
不需要额外的先验条件
缺
点		1.一次波与多次波能量干涉时,自适应相减一次波能量会有损失
2.多次波的压制会有能量残余		1.需要求逆计算1.有较多的调优参数
2.复杂构造的适应性差
3.计算量大		1.计算量大
需要全波场信息,对观测系统和观测数据要求比较高

新窗口打开| 下载CSV


3 总结

本文从方法理论、发展现状、实例比较、优缺点分析等方面深入研究了基于反馈迭代模型的SRME、反数据域法、EPSI、CL-SRME四种自由表面多次波压制方法。可以看到四种方法各有利弊,在实际生产中可结合不同方法的优缺点选择合适的自由表面多次波压制方法。对于成本问题,SRME和反数据域法是比较理想的可考虑方案。而在多次波压制精度上,EPSI和CL-SRME方法更具优势。当然,在已有方法的基础上寻求可以兼顾成本与精度的新方法一直是多次波压制方法研究的追求目标。

参考文献

石颖, 邢小林.

表面多次波压制的研究进展:回顾与展望

[J]. 地球物理学进展, 2011, 26(6):2046-2054.

[本文引用: 1]

Shi Y, Xing X L.

Investigation progress on surface-related multiple suppression:Review and outlook

[J]. Progress in Geophysics, 2011, 26(6):2046-2054.

[本文引用: 1]

张文武. 基于稀疏反演的表面多次波压制方法研究[D]. 大庆: 东北石油大学, 2018.

[本文引用: 1]

Zhang W W. Research on surface-related multiple attenuation by sparse inversion[D]. Daqing: Northeast Petroleum University, 2018.

[本文引用: 1]

Riley D C, Claerbout J F.

2-D multiple reflections

[J]. Digital Library Home, 1976, 41(4):592-620.

[本文引用: 1]

Kennett B L N.

The suppression of surface multiples on seismic records

[J]. Geophysical Prospecting, 1979, 27(3):584-600.

DOI:10.1111/j.1365-2478.1979.tb00987.x      URL     [本文引用: 1]

Berkhout A J.

Seismic migration:Imaging of acoustic energy by wave field extrapolation

[M]. Amsterdam:Elsevier Scientific Pub. Co., 1982.

[本文引用: 1]

Verschuur D J, Berkhout A J, Wapenaar C P A.

Adaptive surface-related multiple elimination

[J]. Geophysics, 1992, 57(9):1166-1177.

DOI:10.1190/1.1443330      URL     [本文引用: 2]

Berkhout A J, Verschuur D J.

Estimation of multiple scattering by iterative inversion,Part 1:Theoretical considerations

[J]. Geophysics, 1997, 62(5):1586-1595.

DOI:10.1190/1.1444261      URL     [本文引用: 4]

Verschuur D J, Berkhout A J.

Estimation of multiple scattering by iterative inversion,Part II:Practical aspects and examples

[J]. Geophysics, 1997, 62(5):1596-1611.

DOI:10.1190/1.1444262      URL     [本文引用: 4]

Verschuur D J. Surface-related multiple elimination,an inversion approach[D]. Delft: Delft University of Technology, 1991.

[本文引用: 1]

Monk D J.

Wave-equation multiple suppression using constrained gross-equalization

[J]. Geophysical Prospecting, 1993, 41(6):725-736.

DOI:10.1111/j.1365-2478.1993.tb00880.x      URL     [本文引用: 1]

Spitz, Simon.

Pattern recognition,spatial predictability, and subtraction of multiple events

[J]. Leading Edge, 1999, 18(1):55-58.

DOI:10.1190/1.1438154      URL     [本文引用: 1]

Guitton A.

Multiple attenuation with multidimensional prediction-error filter

[J]. Geophysics, 2003:57-74.

[本文引用: 1]

Wang Y.

Multiple subtraction using an expanded multichannel matching filter

[J]. Geophysics, 2003, 68(1):346-354.

DOI:10.1190/1.1543220      URL     [本文引用: 1]

陆文凯, 骆毅, 赵波, 等.

基于独立分量分析的多次波自适应相减技术

[J]. 地球物理学报, 2004, 47(5):886-891.

[本文引用: 1]

Lu W K, Luo Y, Zhao B, et al.

Adaptive multiple wave subtraction using independent component analysis

[J]. Chinese Journal of Geophysics, 2004, 47(5):886-891.

[本文引用: 1]

Van Dedem E J. 3D surface-related multiple prediction[D]. Delft: Delft University of Technology, 2002.

[本文引用: 1]

Van Dedem E J, Verschuur D J.

Analysis of surface-related multiples in 3D media

[C]// SEG Expanded Abstracts, 1997, 16(1):1180-1183.

Van Dedem E J, Verschuur D J.

3D surface-related multiple prediction,an inversion approach

[C]// SEG Expanded Abstracts, 2000:1965-1968.

Van Dedem E J, Verschuur D J.

3D surface-related multiple prediction:A sparse inversion approach

[J]. Geophysics, 2005, 70(3):V31-V43.

[本文引用: 1]

Anatoly B, Mohamed T H.

3D surface-related multiple elimination:Data reconstruction and application to field data

[J]. Geophysics, 2006, 71(3):E25-E33.

[本文引用: 1]

石颖, 王维红, 李莹, 等.

基于波动方程三维表面多次波预测方法研究

[J]. 地球物理学报, 2013, 56(6):2023-2032.

[本文引用: 1]

Shi Y, Wang W H, Li Y, et al.

3D surface-related multiple prediction approach investigation based on wave equation

[J]. Chinese Journal of Geophysics, 2013, 56(6):2023-2032.

[本文引用: 1]

井洪亮, 石颖, 李莹, 等.

基于L1/L2范数的表面多次波自适应相减方法

[J]. 石油地球物理勘探, 2015, 50(4):619-625.

[本文引用: 1]

Jing H L, Shi Y, Li Y, et al.

Surface-related multiple adaptive subtraction method based on L1/L2 norm

[J]. OGP, 2015, 50(4):619-625.

[本文引用: 1]

Lopez G A, Verschuur D J.

Closed-Loop SRME — A New Direction in Surface Multiple Removal Algorithms

[C]// EAGE,Extended Abstracts, 2014.

[本文引用: 3]

Berkhout A J.

Seismic processing in the inverse data space

[J]. Geophysics, 2006, 71(4):A29-A33.

[本文引用: 1]

Berkhout A J, Verschuur D J.

Multiple removal and wavelet deconvolution in the inverse data space

[C]// SEG Expanded Abstracts, 2006:2684-2688.

[本文引用: 2]

Kelamis P G, Zhu W, Rufaii K O, et al.

Land multiple attenuation — The future is bright

[C]// SEG Expanded Abstracts, 2006, 25(1):2699-2703.

[本文引用: 1]

Luo Y, Zhu W, Kelamis P G.

Internal multiple reduction in inverse-data domain

[C]// SEG Expanded Abstracts, 2007:1711-1723.

[本文引用: 1]

Berkhout A J, Verschuur D J.

Time lapse processing in the inverse data space

[C]// SEG Expanded Abstracts, 2007:2919-2923.

[本文引用: 1]

Berkhout A J, Verschuur D J.

Seismic processing in the inverse data space,removal of surface —Related and internal multiples

[C]// EAGE Extended Abstracts, 2007.

[本文引用: 1]

马继涛, 陈小宏, 黄小宁.

反数据域压制多次波方法研究

[J]. 石油地球物理勘探, 2009, 44(5):537-542.

[本文引用: 1]

Ma J T, Chen X H, Huang X N.

Studying on multiple elimination in inverse data domain

[J]. OGP, 2009, 44(5):537-542.

[本文引用: 1]

马继涛, Sen M K, 陈小宏.

平面波域反数据处理压制多次波方法研究

[J]. 地球物理学报, 2009, 52(3):808-816.

[本文引用: 2]

Ma J T, Sen M K, Chen X H.

Multiple attenuation using inverse data processing in the plane-wave domain

[J]. Chinese Journal of Geophysics, 2009, 52(3):808-816.

[本文引用: 2]

Ma J T, Sen M K, Chen X H.

Free-surface multiple attenuation using inverse data processing in the coupled plane-wave domain

[J]. Geophysics, 2009, 74(4):V75-V81.

[本文引用: 1]

Van Groenestijn G J, Verschuur D J.

Estimating primaries by sparse inversion and application to near-offset data reconstruction

[J]. Geophysics, 2009, 74(3):A23-A28.

[本文引用: 1]

Van Groenestijn G J, Verschuur D J.

Estimation of primaries by sparse inversion from passive seismic data

[J]. Geophysics, 2010, 75(4):SA61-SA69.

[本文引用: 1]

Van Groenestijn G J A, Ross W.

Primary estimation on OBC data by sparse inversion

[C]// SEG Expanded Abstracts, 2011:311-353.

[本文引用: 1]

Van Groenestijn G J A, Verschuur D J.

Estimation of primaries by sparse inversion applied to up/down wavefields

[C]// SEG Expanded Abstracts, 2009:3143-3147.

Van Groenestijn G J A, Verschuur D J.

Using surface multiples to estimate primaries by sparse inversion from blended data

[J]. Geophysical Prospecting, 2015, 59(1):10-23.

DOI:10.1111/j.1365-2478.2010.00894.x      URL    

Van Groenestijn G J A, Verschuur D J.

Towards a new approach for primary estimation

[C]// SEG Expanded Abstracts, 2008, 27(1):2487-2491.

Van Groenestijn G J A, Verschuur D J.

Incorporating the source array into primary estimation

[C]// EAGE Extended Abstracts, 2010.

Van Groenestijn G J, Verschuur D J.

Estimation of primaries by sparse inversion from blended data

[C]// EAGE Extended Abstracts, 2009.

[本文引用: 1]

刘国昌, 陈小宏, 宋家文.

基于稀疏反演的OBS数据多次波压制方法

[J]. 地球物理学报, 2013, 56(12):4288-4296.

[本文引用: 1]

Liu G C, Chen X H, Song J W.

Estimation of primaries and multiples by sparse inversion for OBS data with integration of streamer data

[J]. Chinese Journal of Geophysics, 2013, 56(12):4288-4296.

[本文引用: 1]

Lin T T Y, Herrmann F J.

Robust estimation of primaries by sparse inversion via one-norm minimization

[J]. Geophysics, 2013, 78(3):R133-R150.

[本文引用: 1]

Lopez G, Verschuur D J.

SRME and estimation of primaries by sparse inversion:a hybrid approach

[C]// SEG Expanded Abstracts, 2012: 1-5.

[本文引用: 1]

Ypma F H C, Verschuur D J.

Estimating primaries by sparse inversion, a generalized approach

[J]. Geophysical Prospecting, 2013, 61(s1):94-108.

DOI:10.1111/j.1365-2478.2012.01095.x      URL     [本文引用: 1]

Angarita G A L, Verschuur D J.

Estimation of primaries by sparse inversion-parameterization via the focal domain

[C]// EAGE Extended Abstracts, 2013.

[本文引用: 1]

Feng F, Wang D L, Zhu H, et al.

Estimating primaries by sparse inversion of the 3D Curvelet transform and the L1-norm constraint

[J]. Applied Geophysics, 2013, 10(2):201-209.

DOI:10.1007/s11770-013-0378-0      URL     [本文引用: 1]

程浩, 王德利, 冯飞, 等.

L1范数约束被动源数据稀疏反演一次波估计

[J]. 地球物理学报, 2015, 58(2):674-684.

[本文引用: 1]

Cheng H, Wang D L, Feng F, et al.

Estimating primaries by sparse inversion of passive-source seismic data with L1-norm constraint

[J]. Chinese Journal of Geophysics, 2015, 58(2):674-684.

[本文引用: 1]

Van Groenestijn G J A.

Estimation of primaries and multiples by sparse inversion

[D]. Delft:Delft University of Technology, 2010.

[本文引用: 1]

王铁兴. 三维稀疏约束反演Closed-loop SRME方法研究[D]. 长春: 吉林大学, 2020:201-209.

[本文引用: 2]

Wang T X. Research on the Closed-loop SRME based on the 3D sparse inversion[D]. Changchun: Jilin University, 2020:201-209.

[本文引用: 2]

Lopez G A, Verschuur D J.

Closed-loop surface-related multiple elimination and its application to simultaneous data reconstruction

[J]. Geophysics, 2015, 80(6):V189-V199.

[本文引用: 1]

Gabriel A, Lopez, Verschuur D J.

Closed-loop surface-related multiple elimination and its application to simultaneous data reconstruction

[J]. Geophysics, 2015, 80(6):V189-V199.

[本文引用: 1]

Lopez G A, Verschuur D J.

3D focal Closed-Loop SRME for shallow water

[C]// SEG Expanded Abstracts, 2015:4418-4422.

[本文引用: 1]

Vrolijk J W, Verschuur D.

Integrated receiver deghosting and closed-loop surface multiple elimination

[C]// SEG Expanded Abstracts, 2016:4481-4486.

[本文引用: 1]

Wang T, Wang D, Sun J, et al.

Closed-loop SRME based on 3D L1-norm sparse inversion

[J]. Acta Geophysica, 2017, 65(6):1145-1152.

DOI:10.1007/s11600-017-0098-6      URL     [本文引用: 1]

Vrolijk J W, Verschuur D.

Integrated receiver deghosting and closed-loop surface multiple elimination

[J]. Geophysics, 2017, 82(4):T133-T141.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com