0 引言
随着国家现代化、城市化的推进,重大工程如大坝、桥梁、隧道建设越来越多,工业与民用建筑日益密集,混凝土为上述建筑的重要材料,混凝土健康监测在结构运行中发挥着越来越大的作用。裂缝是混凝土最为常见的病害之一,如果不能及时发现并处理建筑物关键部位的裂缝,将会带来十分严重的后果。早期裂缝的宽度和长度较小且存在于混凝土内部,摄影和激光扫描检测手段不具有穿透性,难以对内部裂缝进行精准有效的检测[1]。目前国内外研究者提出的对于混凝土内部裂缝的检测方法可大致分为两类:破坏性检测与无损检测[2]。破坏性检测方法主要包括凿槽、钻孔取心、孔内电视法,这些方法对混凝土结构具有破坏性,检测效率低,难以大量多次进行。无损检测的典型方法有射线探伤法、超声波检测法、电磁波检测法[3]:射线探伤法在使用过程中如果操作不当会对人体造成很大伤害,且射线的穿透能力不强,目前很少使用;超声波检测法主要是通过超声波在混凝土传播后发生的波形变化来判断混凝土的内部情况,不能用于不平整的外表面和复杂的建筑体裂缝检测。
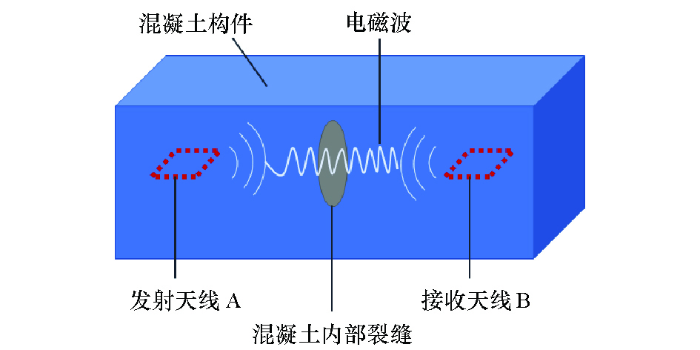
电磁波探测法具有分辨率高、探测速度快、探测范围广、探测过程连续等优点。1904~1930年是电磁波检测法的萌芽阶段,当时该领域最具代表性的Hulsenbeek学者首次提出根据介质变化会使电磁波产生反射的原理,利用电磁波技术探测地下结构[4]。1950年至今人们对电磁波探测技术的运用逐渐成熟,现如今最为常用的手段是利用探地雷达向混凝土内传送电磁波[5]。探地雷达工作时,在主机控制下,脉冲源产生周期性的毫微秒脉冲信号并直接馈送给发射天线,经由发射天线耦合到地下的信号,在传播路径上遇到不同介质的分界面(裂缝腔体与混凝土的分界面)则产生反射信号;位于地面上的接收天线将接收到的地下反射回波直接传输到接收机,信号经接收机整形和放大等处理后,再经电缆传输到雷达主机和微机,然后再对数据进行处理[5,6,7]。可见,探地雷达对混凝土内部裂缝的检测要经过一系列繁琐的步骤,且容易受到外部诸多条件的影响,不具有实时性、便捷性、高效性。针对以上问题,本文提出一种新的裂缝传感检测法。该方法直接将建筑体内的钢筋作为天线,并由钢筋天线向周围的混凝土发送电磁波,通过天线端口的S参数判断混凝土内的裂缝情况。钢筋是建筑体内固有的一部分,将钢筋作为传感天线能够做到对混凝土内部裂缝实时检测,无需额外装配传感器,且其寿命与结构寿命等长,如能用于混凝土裂缝传感,将可能孕育混凝土裂缝监测变革性成果。
1 电磁波传播模型的构建
1.1 混凝土内部裂缝对电磁波传播的影响分析
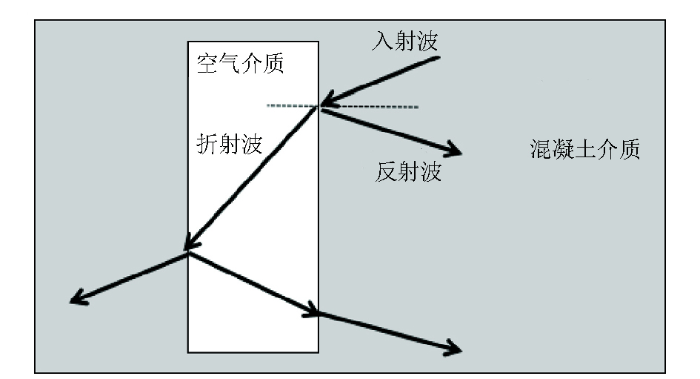
图1
图1
电磁波在混凝土裂缝的传播情况
Fig.1
Propagation of electromagnetic wave in concrete cracks
1.2 S21参数
1.3 混凝土内部钢筋的天线功能化
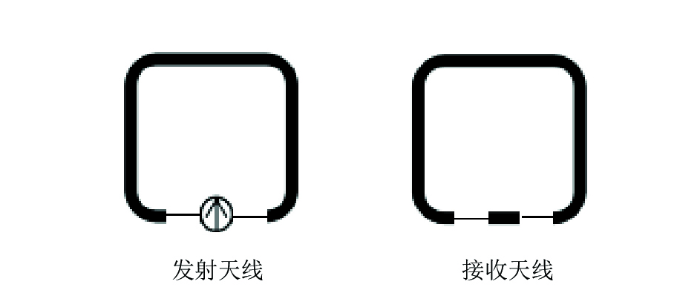
图2
1.4 混凝土构件内部电磁波传播模型
图3
2 仿真模拟分析
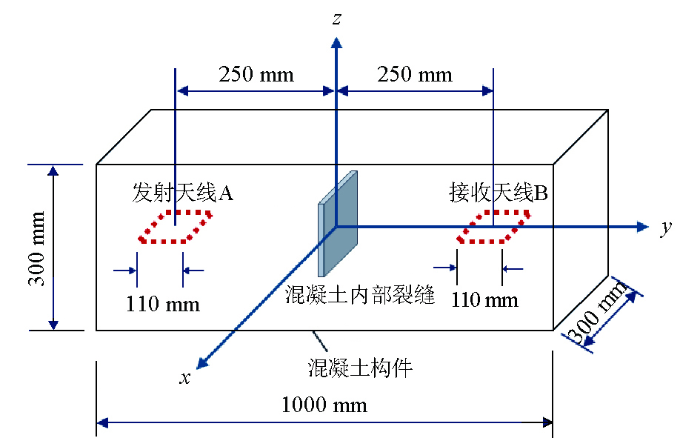
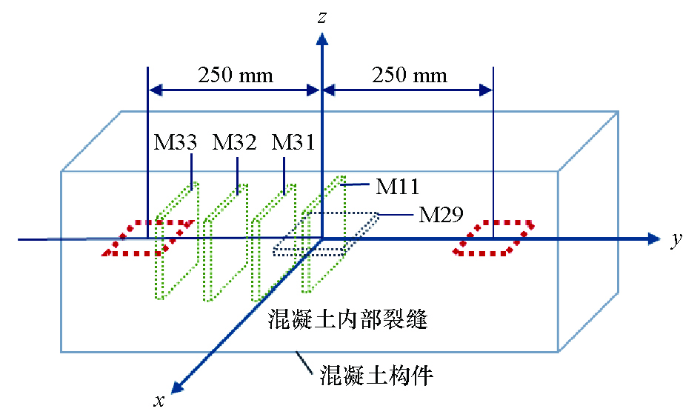
采用三维全波电磁场仿真软件Computer Simulation Technology(CST)进行仿真模拟分析,选择时域求解器完成求解,用MATLAB对CST仿真结果后处理,可得到天线的S21参数幅值曲线。以长×宽×高=1 000 mm×300 mm×300 mm的长方体混凝土构件为仿真模拟对象(图4),混凝土材质选择软件自带材料库中的Concrete(one year old)。以长方体构件的几何中心作为坐标原点建立笛卡尔坐标系,在其中嵌入一对倒角矩形环形线天线A和B作为发射天线和接收天线,天线环面平行于xoy面(图2、图3),天线的材质选择软件自带材料库中的Steel-1008钢材,在发射天线A的端口处设置激励源。基于混凝土实际结构以及天线辐射功率计算方法[14,15,16,17,18],环形天线边长设为110 mm,横截面直径为3 mm,2个天线的中心相距500 mm,天线A、B的中心点坐标分别为(0,-250,0)和(0,250,0),不设置裂缝。该模型为无裂缝基准模型M0。
图4
图5
表1 仿真模型参数信息
Table 1
| 模型编号 | 裂缝中心点位置 | 变化参数 |
|---|---|---|
| M0 | 无裂缝 | |
| M11 | 坐标原点 | 垂直裂缝,厚1 mm |
| M13 | 坐标原点 | 垂直裂缝,厚3 mm |
| M15 | 坐标原点 | 垂直裂缝,厚5 mm |
| M17 | 坐标原点 | 垂直裂缝,厚7 mm |
| M23 | 坐标原点 | 倾斜裂缝,与xoz平面夹角30° |
| M26 | 坐标原点 | 倾斜裂缝,与xoz平面夹角60° |
| M29 | 坐标原点 | 倾斜裂缝,与xoz平面夹角90° |
| M31 | 沿y轴偏移 | 垂直裂缝,偏移至-56.5 mm |
| M32 | 沿y轴偏移 | 垂直裂缝,偏移至-113 mm |
| M33 | 沿y轴偏移 | 垂直裂缝,偏移至-169.5 mm |
3 仿真结果
3.1 有裂缝与无裂缝对比
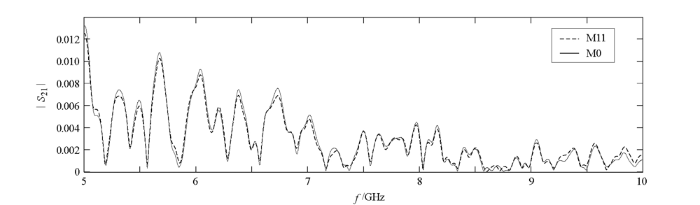
图6
图6
S21参数幅值在5~10 GHz的频率范围内有裂缝与无裂缝合并
Fig.6
Combined graph of S21 parameters with and without cracks in the frequency range of 5~10 GHz
绘制出比值
图7
图7
S21参数在5~10 GHz的频率范围内有裂缝与无裂缝的频率特征
Fig.7
S21 parameter takes logarithm as the ratio of crack and no crack in the frequency range of 5~10 GHz
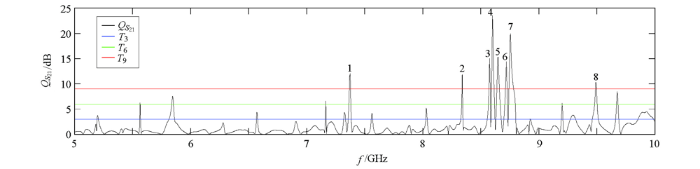
根据每一个特征频带的上限频率fmax和下限频率fmin,求出各个频带的带宽BW和中心频率fo:
表2 极易辨识特征频参数
Table 2
| 序号 | 中心频率/GHz | 带宽/MHz | 最大比值/dB |
|---|---|---|---|
| 1 | 7.373 | 11 | 10.961 |
| 2 | 8.34 | 5 | 12.751 |
| 3 | 8.576 | 11 | 15.596 |
| 4 | 8.603 | 22 | 24.028 |
| 5 | 8.649 | 22 | 13.959 |
| 6 | 8.719 | 14 | 15.022 |
| 7 | 8.762 | 41 | 19.699 |
| 8 | 9.492 | 10 | 10.619 |
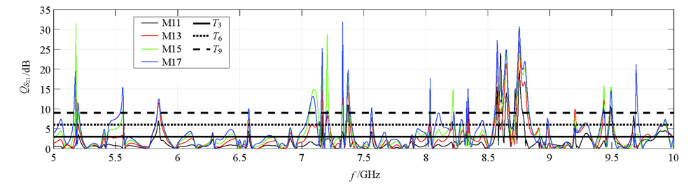
3.2 不同裂缝厚度对检测效果的影响
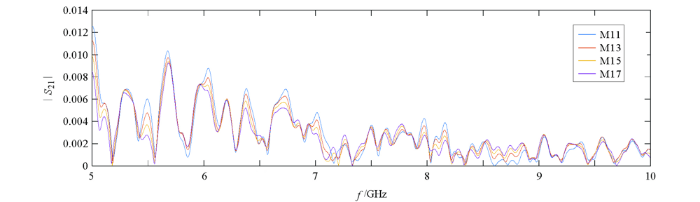
图8
图8
5~10 GHz频率范围内不同裂缝厚度的S21模值
Fig.8
The modulus of S21 parameters with different crack thickness in the frequency range of 5~10 GHz
利用式(2)分别计算出M13、M15、M17的S21幅值与M0模型的S21幅值比值,即
图9
图9
5~10 GHz频率范围内不同裂缝厚度的
Fig.9
The ratio
表3 不同裂缝厚度辨识效果对比
Table 3
| 裂缝模型 | 可以辨 识/段 | 容易辨 识/段 | 极易辨 识/段 | 公有中心频率 带宽/MHz |
|---|---|---|---|---|
| M11 | 21 | 13 | 8 | 7 |
| M13 | 27 | 22 | 13 | 20 |
| M16 | 33 | 22 | 16 | 24 |
| M17 | 35 | 28 | 20 | 35 |
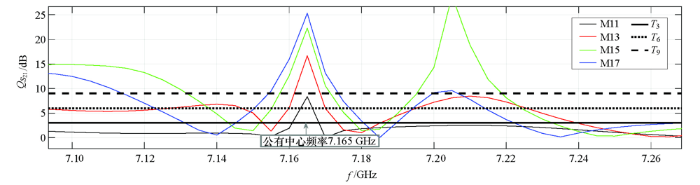
图10
图10
不同厚度裂缝公有中心频率附近的特征频带
Fig.10
Characteristic frequency band near common center frequency of crack with different thickness
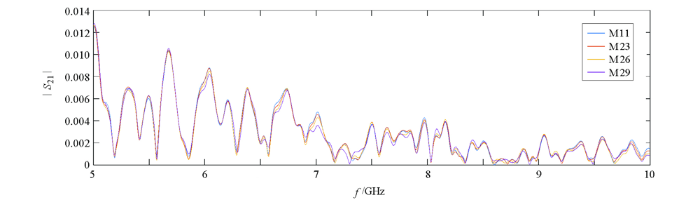
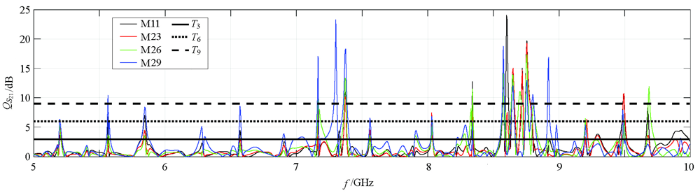
3.3 不同裂缝角度对S参数的影响
图11
图11
5~10 GHz频率范围内不同裂缝角度的S21参数之模值
Fig.11
The modulus of S21 parameters with different crack angles in the frequency range of 5~10 GHz
表4 不同裂缝角度辨识效果对比
Table 4
| 裂缝模型 | 可以辨识 /段 | 容易辨识 /段 | 极易辨识 /段 | 公有中心频率 带宽/MHz |
|---|---|---|---|---|
| M11 | 21 | 13 | 8 | 29 |
| M23 | 17 | 11 | 6 | 37 |
| M26 | 19 | 13 | 7 | 34 |
| M29 | 25 | 15 | 9 | 43 |
图12
图12
S21幅值在5~10 GHz的频率范围内有裂缝与无裂缝的比值
Fig.12
The ratio
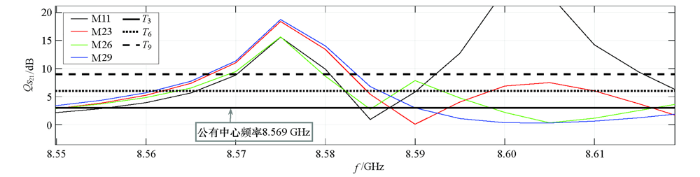
裂缝角度从M26到M29极易辨识特征频带分布变化较明显,表现为中频段(7~8 GHz)的极易识别特征频带数增加了2段,而高频段(9~10 GHz)内的极易识别特征频带减少了1段。同样地,记录每一段可辨识特征频带的带宽和中心频率,发现中心频率为8.569 GHz的可辨识特征频带共同存在于4种不同角度的裂缝中,其带宽分别为0.029、0.037、0.034、0.043 GHz,如图13所示。
图13
图13
不同角度裂缝公有中心频率附近的特征频带
Fig.13
Characteristic frequency band near common center frequency of crack with different angles
由此可见,当裂缝处于某个位置并在一定范围内变换角度时,采用8.569 GHz的电磁波,通过计算带宽来辨识裂缝角度。
3.4 不同裂缝位置对S参数的影响
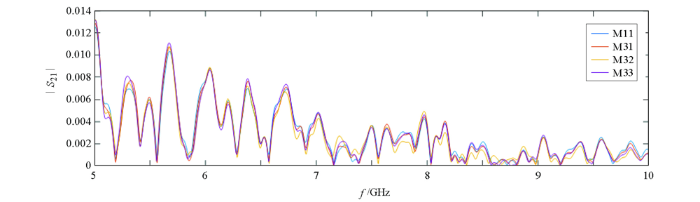
通过M11、M31、M32、M33的仿真结果,可以发现不同裂缝位置对S21幅值参数的影响。M11、M31、M32、M33的S21幅值仿真得出的结果如图14所示,可以看出,5~10 GHz率范围内不同裂缝位置对S21的幅值有明显影响,但呈现出较为复杂的非线性关系,即裂缝和天线1的距离与S21幅值不能用简单的线性关系描述。然后依然利用上文所述的方法对该组数据进行处理,即将裂缝模型M31、M32、M33的S21参数幅值分别与M0模型的S21参数幅值利用式(2)求比值
图14
图14
5~10 GHz频率范围内不同裂缝位置的S21参数之模值
Fig.14
The modulus of S21 parameters with different crack locations in the frequency range of 5~10 GHz
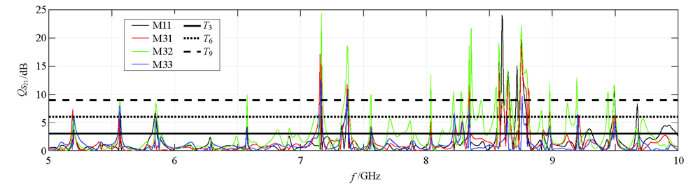
图15
图15
S21幅值在5~10 GHz的频率范围内有裂缝与无裂缝的比值
Fig.15
The ratio
表5 不同裂缝位置辨识效果对比
Table 5
| 裂缝模型 | 可以辨识 /段 | 容易辨识 /段 | 极易辨识 /段 | 公有中心频率 带宽/MHz |
|---|---|---|---|---|
| M11 | 21 | 13 | 8 | 65 |
| M31 | 22 | 12 | 8 | 66 |
| M32 | 30 | 24 | 18 | 105 |
| M33 | 16 | 7 | 3 | 45 |
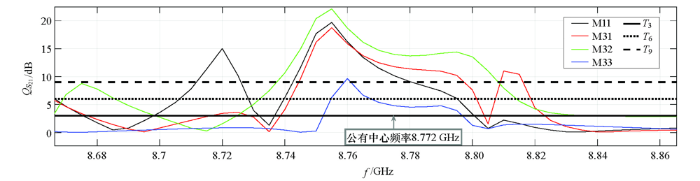
再次利用上文中的方法计算所有可辨识特征频带的带宽和中心频率,发现其中有一段中心频率为8.772 GHz的可辨识特征频带存在于4个不同位置的裂缝中,其带宽分别为 0.065、0.066、0.105、0.045 GHz,如图16所示,通过中心频率为8.772 GHz的电磁波可以检测裂缝位置。
图16
图16
不同位置裂缝公有中心频率附近的特征频带
Fig.16
Characteristic frequency band near common center frequency of crack with different locations
4 结论
本文通过在混凝土中嵌入一对钢筋环状天线并由天线向混凝土内部发射电磁波进行建模仿真,通过改变裂缝厚度、裂缝角度、裂缝位置来分析S21幅值参数在5~10 GHz范围内的数据规律,探究混凝土内钢筋作为传感器检测裂缝的新方法,由仿真结果可以得出:
1) 5~10 GHz范围内,可以以钢筋作为天线,通过分析钢筋天线对的S21幅值参数,可以辨识混凝土内裂缝。
2) 裂缝的厚度、角度、位置的改变均会导致S21参数幅值上的改变,从而影响特征频带的数量、带宽、中心频率。5~10 GHz范围内,通过S21幅值参数,可以计算厚度、角度、位置的裂缝参数。
3) 通过本文的计算模型,发现如下规律:特征频率为7.165 GHz时,裂缝厚度越厚,带宽越大;特征频率为8.569 GHz时,裂缝角度越大,带宽越大。
本文采用电磁波仿真软件,探究了应用钢筋作为混凝土内置天线的混凝土裂缝状的电磁波传播的规律,发现通过钢筋天线对S21幅值分析可以判断混凝土裂缝状态,有望实现一种无需额外装配传感器,且其寿命与结构寿命等长的混凝土裂缝检测变革性传感方法。但这种传感方法对于实际工程应用,还需要对基于钢筋天线的混凝土裂缝传感进行充分的理论分析与实验验证。
参考文献
车载探地雷达地下目标实时探测法
[J].
Real time detection of underground targets by vehicle borne ground penetrating radar
[J].
水工大体积混凝土裂缝检测
[J].
Crack detection of hydraulic mass concrete
[J].
三维探地雷达在城市市政管线渗漏探测中的应用
[J].
Application of 3D ground penetrating radar in leakage detection of municipal pipelines
[J].
应用电磁波探测混凝土管道的空洞缺陷
[D].
Application of electromagnetic wave to detect cavity defects in concrete pipes
[D].
基于探地雷达属性分析的典型岩溶不良地质识别方法
[J].
Identification method of typical karst unfavorable geology based on GPR attribute analysis
[J].
Characterization of collapsed paleocave systems using GPR attributes
[J].DOI:10.1016/j.jappgeo.2014.01.007 URL [本文引用: 1]
探地雷达无损检测方法评述
[J].
Review of ground penetrating radar nondestructive testing methods
[J].
大深度高精度广域电磁勘探理论与技术
[J].
Theory and technology of wide field electromagnetic method
[J].
基于探地雷达的混凝土无损检测方法研究
[D].
Research on concrete nondestructive testing method based on ground penetrating radar
[D].
位移电流及反射与折射对高频电磁波探测深度的影响
[J].
Influence of displacement current,reflection and refraction on detection depth of high frequency electromagnetic wave
[J].
电磁波在混凝土材料表面的透射率研究
[J].
Study on transmission of electromagnetic wave on concrete surface
[J].
Electromagnetic energy and data transfer in biological tissues using loop antennas
[J].DOI:10.1016/j.procs.2013.06.124 URL [本文引用: 1]
宽载波频率大带宽超短波射频电路关键技术研究与验证
[D].
Research and verification of key technologies of wide carrier frequency and large bandwidth ultra short wave radio frequency circuit
[D].
一种超宽带小型化探地雷达天线的设计
[J].
Design of a miniaturized UWB GPR antenna
[J].