0 引言
高精度重力测量可以为区域地质构造研究、资源与能源勘查等提供重要的基础数据。野外起伏观测面采集的重力数据,经过各项校正得到的重力异常仍然是原起伏观测面上的异常,反映地下密度不均匀体在起伏观测面上的重力效应[1]。频率域算法是地球物理领域的一种常用快速算法,已广泛应用于重力数据处理与反演解释,比如频率域延拓[1,2]、频率域优化滤波[3]、频率域界面反演[4]、频率域三维成像[5]等。然而,这些频率域算法通常要求重力异常所对应的观测面为平面。在观测面起伏较大情况下,若对起伏面重力数据直接应用常规频率域算法做处理与反演,则将带来不可忽略的处理偏差。因此,在起伏观测面条件下,重力异常数据从起伏观测面化到平面上,即曲化平,是开展频率域精细处理解释的必要步骤。
当前重力数据的曲化平方法较多,Pilkington等[6]将其分为基于源和基于场的两大类。基于源的方法主要有等效源法[7,8,9,10,11,12],它先对起伏观测面异常反演获得地下等效场源,然后再正演计算等效源在任意水平面引起的异常,该类方法通常计算量较大,适用于中、小规模数据的曲化平处理。基于场的方法有有限调和级数法[13]、泰勒级数法[14,15]、有限元法[16,17]、积分法[18,19]、逐次逼近法[20]等,该类方法无需反演场源,通常需要向上延拓或向下延拓到某中间层面进而获取最终平面的异常。向上延拓是稳定的,但向下延拓通常是不稳定的,这是由于它具有放大作用,对高频噪声干扰比较敏感,延拓跨度越大,高频干扰越严重。因此,基于向下延拓的曲化平方法一般迭代收敛速度慢、精度有限,仅适用于延拓跨度小的曲化平。
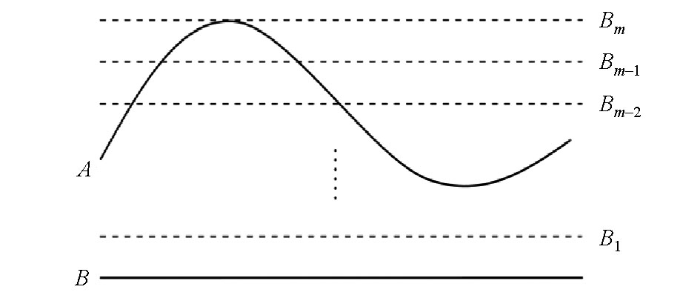
徐世浙等[21]提出了位场(重、磁场)曲化平的插值—迭代法,属于基于场的方法类,它计算简单快速,可以实现延拓跨度达10~20倍点距的大规模数据的稳定曲化平。该方法基本思路是,将起伏观测面(A)的顶部水平面(Bm)与底部水平面(B)之间的空间剖分为若干等间距的中间层水平面(Bi),见图1所示;接着,把起伏观测面(A)的位场值放到底部水平面(B)并作为该水平面的位场初始值;然后,通过频率域向上延拓计算出各中间水平面(Bi)的位场值,进而从各中间水平面(Bi)集合的位场值插值出起伏观测面(A)的位场近似值;之后,计算起伏观测面(A)的位场实测值与近似值的残差,并用于对底部水平面(B)的位场值进行修正;如此反复迭代,直至起伏观测面(A)的位场实测值与近似值的残差达到误差容限。
图1
图1
插值—迭代法曲化平示意
Fig.1
The diagram of interpolation-iteration method for gravity anomaly continuation from undulating surface to plane
1 方法原理
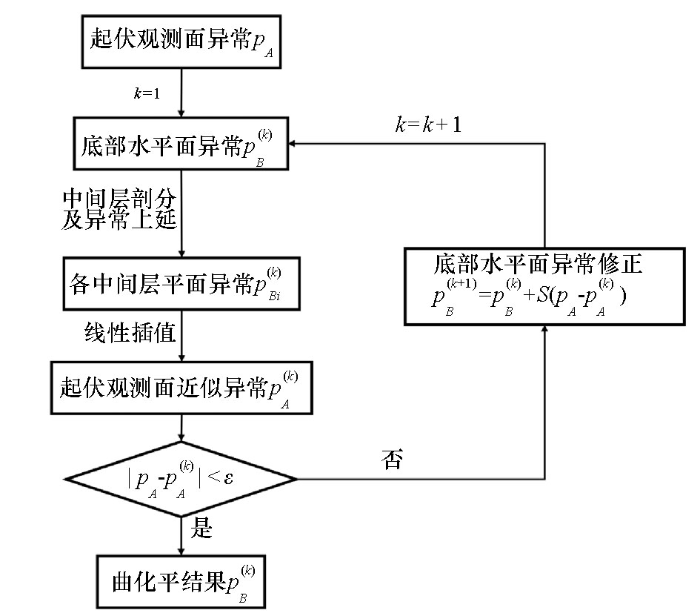
本文算法流程如下图2所示。首先,将起伏观测面A的实测位场数据pA直接赋值到底部水平面B上,作为底部水平面B的位场初值
图2
图2
本文改进的插值—迭代法算法流程
Fig.2
The workflow of the modified interpolation-iteration method
接着,利用频率域向上延拓方法[2]将底部水平面B的位场初值
然后,计算起伏观测面A的位场实测值pA与近似值
在徐世浙等[21]的插值—迭代方法中,修正因子S取常数,且通常取为1,即观测面上各测点的修正因子相同,导致在相同迭代次数下,观测面起伏变化大的地方曲化平迭代收敛速度慢、效果差些。因此,本文对修正因子S做了改进,采用与起伏观测面相关的修正因子,从而加快曲化平迭代收敛速度,提升曲化平效果。本文的修正因子公式如下:
其中,T为起伏观测面高程,Tmin和Tmax分别是起伏观测面高程的最小值和最大值。可知,观测面起伏越大,修正因子S将越大,曲化平收敛速度将越快,反之,观测面起伏越小,修正因子S将越小,曲化平收敛速度将越慢。一般,n取非负数,若n取值过大,则修正因子S将越大;反之,n取值越小,修正因子S将越小;当n=0时,修正因子S=1,等效于徐世浙等[21]的算法。
之后,对式(2)得到的底部水平面B的位场修正值,重复上述两个步骤,依次迭代修正,直到起伏观测面A的位场实测值pA与近似值
2 理论模型数据试验
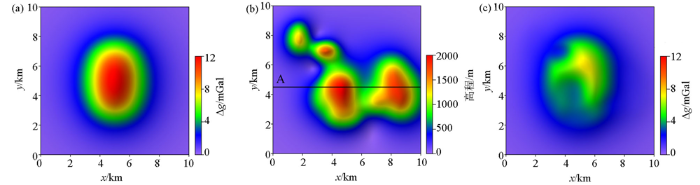
理论模型为一个直立长方体,长、宽、高分别为 2 000、4 000、1 000 m,中心埋深1 500 m,剩余密度为1.0 g/cm3。假定测网E向和N向范围均为0~10 km、点距均为0.1 km,则理论模型在海拔0 km的水平面上产生的理论重力异常如图3a所示,异常等值线为近椭圆状,最小值为0.23 mGal,最大值为12.65 mGal,平均值为2.41 mGal。假定起伏观测面高程如图3b所示,高程最小值为1.46 m,最大值为2 023.55 m,观测面高差是测网点距的20多倍。理论模型在起伏观测面上产生的理论重力异常如图3c所示,异常等值线为不规则形状,且与起伏观测面形状有一定相关,异常最小值为0.23 mGal,最大值为7.52 mGal,平均值为1.88 mGal。因此,受观测面起伏影响,理论重力异常变为复杂,难以直接处理解释,值得优先进行曲化平处理。
图3
图3
理论模型起伏观测面与重力异常
a—海拔0 m平面的理论重力异常;b—起伏观测面高程;c—起伏观测面的理论重力异常
Fig.3
Undulating observation surface of theoretical model and its gravity anomaly
a—theoretical gravity anomaly at 0 m altitude;b—elevation of undulating observation surface;c—theoretical gravity anomaly at undulating observation surface
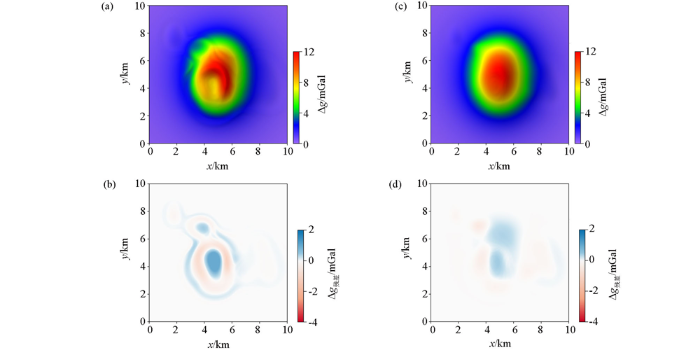
图4
图4
不同曲化平方法的结果及与海拔0 m平面理论重力异常对比
a、b—常规插值-迭代法曲化平结果及与海拔0 m平面理论重力异常残差;c、d—本文改进的插值-迭代法曲化平结果及与海拔0 m平面理论重力异常残差
Fig.4
Comparison between the results of different interpolation-iteration methods and the gravity forward values of plane surface
a、b—the result of the routine interpolation-iteration method for continuation from undulating surface to plane and its deviation from the values of plane surface;c、d—the result of the modified interpolation-iteration method and its deviation from the values of plane surface
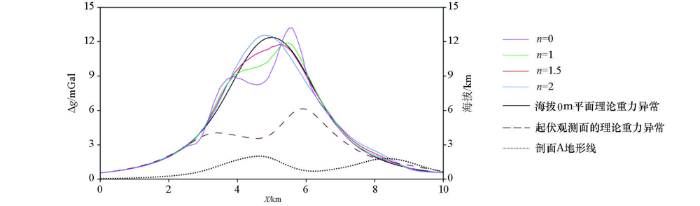
图5显示了剖面A不同曲化平方法结果与起伏观测面、海拔0 m平面的理论重力异常、起伏观测面高程的对比。观察发现,水平面的理论重力异常出现一个异常峰值,对应地下密度异常体,起伏观测面下的重力异常出现两个异常峰值,其位置与起伏观测面相对应,这说明起伏观测面扭曲了地下密度体的异常信息,观测面起伏越高,扭曲作用越大。n的取值与实际研究区观测面起伏程度相关,n=0时,S为常数1,等效于徐世浙等[21]的算法,其均方根误差为0.1551 mGal;n=1时,其均方根误差0.044 5 mGal;n=1.5时,其均方根误差最小,为0.028 7 mGal;n=2时,其均方根误差0.079 4 mGal,故本文选n=1.5。
图5
改进的插值—迭代法有效增强了信号,曲化平后其最小值为0.23 mGal,最大值为12.33 mGal,结果与海拔0 m平面理论重力异常差别较小。异常残差最小值为-0.86 mGal,最大值为1.03 mGal,标准差为0.17 mGal,我们分析这一微小差异是由高程差距引起收敛速度不一致产生的。因此,与常规插值—迭代法相比,本文改进的插值—迭代法曲化平结果更接近海拔0 m平面理论重力异常值,效果更优,适用于大规模数据、复杂起伏观测面、大延拓跨度的曲化平。
3 实际数据试验
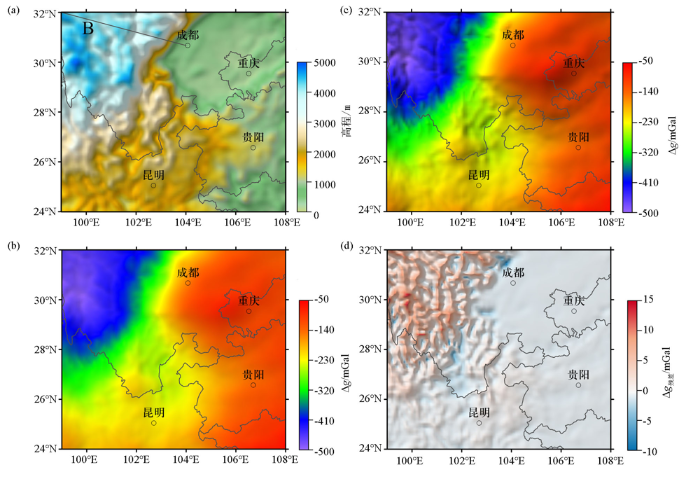
川滇地区构造上位于印支块体、青藏高原块体和扬子块体的交汇处,区域构造动力作用复杂,在缅甸弧东向俯冲、印度板块藏东构造结NE向楔体挤出和俯冲、青藏高原隆升和SE向挤出等共同作用下,该地区整体向E—SE方向挤出,形成了大陆内部典型的剪切、拉张和推覆构造,表现出地壳变形速率高、断层运动剧烈、强震原地复发周期短等区域特征。因此,川滇地区是研究青藏高原隆升过程与大陆强震孕育机理的天然实验场,也是我国区域防震减灾的重要地区。高精度重力数据是川滇地区深部结构与构造研究的基础数据。由于该地区地形上呈现青藏高原、云贵高原、四川盆地等复杂、多样化的起伏形态,因此对该地区起伏地形面的重力异常数据作常规频率域处理和解释应用之前,值得优先作曲化平处理。
本文从ICGEM官网(
图6
图6
川滇地区曲化平前后重力异常对比
a—川滇地区地形高程;b—去噪后的布格重力异常;c—本文改进插值—迭代法曲化平后布格重力异常;d—曲化平前后的异常残差
Fig.6
The Bouguer gravity comparison before and after continuation from undulating surface to plane of Sichuan-Yunnan region
a—the elevation of Sichuan-Yunnan region;b—the denoised Bouguer gravity anomaly;c—the Bouguer gravity anomaly after continuation from undulating surface to plane by using the modified interpolation-iteration method;d—the anomaly deviations before and after continuation from undulating surface to plane
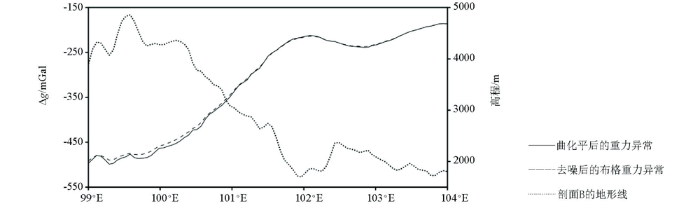
图7
图7
剖面B的对比
Fig.7
The gravity anomaly comparison and the elevation along profile B
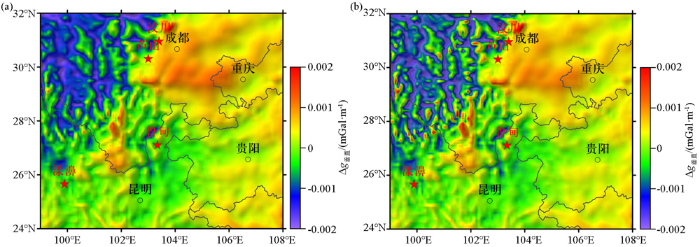
图8
图8
川滇地区曲化平前后垂向导数对比
a—布格重力异常的垂向导数;b—曲化平后布格重力异常的垂向导数
Fig.8
The vertical derivative of Bouguer gravity comparison before and after continuation from undulating surface to plane of Sichuan-Yunnan region
a—the vertical derivative of Bouguer gravity anomaly;b—the vertical derivative of Bouguer gravity
图8中标注了2008年汶川8级地震、2013年芦山7级地震、2014年鲁甸6.5级地震、2021年漾濞6.4级地震的震中位置,易见经过曲化平这些地震震中周缘地区的重力异常变化特征更为鲜明,这有助于后续的深部结构与构造解释研究。
4 结论与讨论
本文在重力异常曲化平的常规插值—迭代法基础上给出了一种改进的插值—迭代法,即在异常迭代修正过程中引入起伏观测面修正因子,加快曲化平迭代收敛,促进曲化平效果提升,实现适用于观测面起伏较大、延拓跨度较大的复杂条件下重力异常曲化平。理论模型和川滇地区实际数据试验验证了本文方法的有效性,效果优于常规插值—迭代法。本文改进的插值—迭代方法不仅适用于重力异常数据,也适用于磁异常数据以及梯度、三分量等数据。本文曲化平的结果可进一步通过常规平化平、平化曲处理实现任意平面或曲面的延拓。
参考文献
Preferential filtering for gravity anomaly separation
[J].DOI:10.1016/j.cageo.2012.09.012 URL [本文引用: 1]
The inversion and interpretation of gravity anomalies
[J].DOI:10.1190/1.1440444 URL [本文引用: 1]
A wavenumber-domain iterative approach for rapid 3-D imaging of gravity anomalies and gradients
[J].DOI:10.1109/Access.6287639 URL [本文引用: 1]
Potential field continuation between arbitrary surfaces-Comparing methods
[J].DOI:10.1190/geo2016-0210.1 URL [本文引用: 1]
The equivalent source technique
[J].DOI:10.1190/1.1439996 URL [本文引用: 1]
Equivalent sources used as an analytic base for processing total magnetic field profiles
[J].DOI:10.1190/1.1440344 URL [本文引用: 1]
Reduction of magnetic and gravity data on an arbitrary surface acquired in a region of high topographic relief
[J].DOI:10.1190/1.1440802 URL [本文引用: 1]
Continuation of potential fields between arbitrary surfaces
[J].DOI:10.1190/1.1441707 URL [本文引用: 1]
Reduction of potential field data to a horizontal plane
[J].DOI:10.1190/1.1442866 URL [本文引用: 1]
Correction of topographic distortions in potential-field data: A fast and accurate approach
[J].DOI:10.1190/1.1443434 URL [本文引用: 1]
Reduction of unevenly spaced potential field data to a horizontal plane by means of finite harmonic series
[J].
Frequency-domain reduction of potential field measurements to a horizontal plane
[J].DOI:10.1016/0016-7142(87)90083-4 URL [本文引用: 1]
Draping corrections for aeromagnetic data: Line versus grid-based approaches
[J].DOI:10.1071/EG01095 URL [本文引用: 1]
重磁场的有限元法曲化平
[J].
The finite element method of gravity and magnetic field
[J].
The boundary element method in geophysics
[M].
A new method for continuation of 3D potential fields to a horizontal plane
[J].DOI:10.1190/1.1635045 URL [本文引用: 1]
位场延拓的积分—迭代法
[J].
The interpolation-iteration method for continuation of potential fields
[J].
位场曲化平积分方程的迭代解
[J].
Iterative solution of integral equation for potential field continuation from irregular surface to a horizontal plane
[J].
位场曲化平的插值—迭代法
[J].
The interpolation-iteration method for potential fields continuation from undulating surface to plane
[J].