基于曲波稀疏变换的拉伸校正方法

doi:10.11720/wtyht.2022.1328

基于曲波稀疏变换的拉伸校正方法

刘仕友^,¹, 张明林², 宋维琪²

1.中海石油(中国)有限公司海南分公司,海南海口 570311

2.中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

Stretch correction method based on Curvelet sparse transform

LIU Shi-You^,¹, ZHANG Ming-Lin², SONG Wei-Qi²

1. Hainan Branch of CNOOC (China) Co.,Ltd., Haikou 570311, China

2. School of Geosciences, China University of Petroleum (East China), Qingdao 266580, China

责任编辑: 叶佩

收稿日期: 2021-06-15 修回日期: 2021-11-26

基金资助:

中海石油(中国)有限公司重大科技项目“南海西部油田上产2000万方关键技术研究”(CNOOC-KJ135ZDXM38ZJ02ZJ)

Received: 2021-06-15 Revised: 2021-11-26

作者简介 About authors

刘仕友(1982-),男,高级工程师,2007 年毕业于中国石油大学(华东),主要从事储层预测及烃类检测工作。Email: liushiyou@139.com

摘要

动校正是地震数据处理中的重要步骤,但它在校正过程中会产生子波拉伸畸变效应,随着偏移距的增大,会出现主频降低、振幅扩大的现象。由于存在拉伸畸变,同相轴未被拉平,导致非同相叠加,会引起水平叠加剖面的频率失真和分辨率下降,因此,拉伸校正是提高水平叠加剖面分辨率的关键。子波拉伸畸变在曲波稀疏域中是不相干的,可以将拉伸校正视为是一个非线性优化过程。通过度量稀疏域中数据的稀疏性,使用一种快速有效的算法,来优化子波拉伸畸变生成的非线性问题,最终实现消除子波拉伸畸变的目的。曲波稀疏变换拉伸校正方法能够消除由动校正带来的子波拉伸畸变,恢复远偏移距处的高频信息,校平同相轴。综合模型数据和实际资料处理,曲波稀疏拉伸校正方法能够显著提高水平叠加剖面的分辨率。

关键词： 叠前道集处理; 拉伸校正; 曲波变换; 稀疏重建

Abstract

NMO correction is an important step in seismic data processing, but it will produce the wavelet stretching distortion effect in the process of correction. With the increase of offset, the dominant frequency will decrease and the amplitude will increase.Due to stretch distortion, the in-phase axis is not leveled, leading to non-in-phase stacking, which will lead to frequency distortion and resolution decrease of horizontal stacking profile. Therefore, stretch correction is the key to improve the resolution of horizontal stacking profile.The stretching distortion of wavelet is incoherent in the curved sparse domain, and the stretching correction can be regarded as a nonlinear optimization process.By measuring the sparsity of the data in the sparse domain, a fast and effective algorithm is used to optimize the nonlinear problem generated by the wavelet stretching distortion, and finally the purpose of eliminating the wavelet stretching distortion is realized.The curved sparse transform stretching correction method can eliminate the wavelet stretching distortion caused by NMO correction, recover the high frequency information at the far offset and level the in-phase axis.Combining model data and actual data processing, the curved wave sparse stretch correction method can significantly improve the resolution of horizontal superposition profile.

Keywords： pre-stack gather processing; stretch correction; curvelet transform; sparse reconstruction

PDF (8528KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘仕友, 张明林, 宋维琪. 基于曲波稀疏变换的拉伸校正方法[J]. 物探与化探, 2022, 46(1): 114-122 doi:10.11720/wtyht.2022.1328

LIU Shi-You, ZHANG Ming-Lin, SONG Wei-Qi. Stretch correction method based on Curvelet sparse transform[J]. Geophysical and Geochemical Exploration, 2022, 46(1): 114-122 doi:10.11720/wtyht.2022.1328

0 引言

动校正是地震数据处理中的重要一环,动校正的结果直接影响水平叠加、AVO分析、反演等后续处理过程^[1]。但是,常规动校正由于其固有的特性,动校正之后的同相轴会存在没有被校平的情况,产生较为复杂的拉伸畸变效应,一般表现为远偏移距处的频率降低、振幅变大^[2]。对于畸变严重的部分,通常采用切除的方法来降低畸变的影响。然而,切除的部分缩短了有效扩展长度、降低了覆盖次数,从而降低了叠加剖面的分辨率^[3]。

Rupert和Chun提出了整体搬家(bock move sum,BMS)方法^[4],在BMS方法中,小时间窗口中的地震数据可以实现数据的块移动,避免在每个点上出现不同的校正值而引起拉伸畸变。然而,在BMS中数据块的大小需要与小波周期相同,并且在块边界上会发生不连续的现象。Shatilo和Aminzadeh提出了一种固定时差动校正(constant normal move out,CNMO)^[5],CNMO方法与传统逐点搬家动校正方法有着明显的区别,那就是在一个固定的时窗内对所有的地震道按照走时公式采用了固定的时差常数来校平CMP道集上的反射同相轴,这种方法校正后的数据分辨率更高,从而避免了大孔径处信号的频率失真,在一定程度上保留了更多的长偏移距信号,CNMO的缺陷是在长偏移距处产生了假同相轴。Hicks在叠加过程中使用抛物线Radon变换来消除NMO拉伸畸变^[6]。然而,该方法在存在噪声的情况下是不稳定的,并且不能有效地校正振幅较弱的区域。Trickett开发了一种无拉伸叠加方法^[7],将NMO校正和叠加两步替换为零偏移叠加的单步反演,该方法将BMS技术应用于反演,降低了相邻块间不连续性。崔宝文等通过傅里叶变换,把时间偏移距域地震数据转化为频率域,将远偏移距的频谱替换为近偏移距的频谱^[8],避免了拉伸,但存在相互干扰的情况。Kazemi和Siahkoohi提出一种避免NMO拉伸的局部拉伸调零方法^[9],根据速度分析的结果,将数据分成不同的时间块。该方法消除了产生NMO拉伸的插值数据样本的理论曲线,从而保留了一般比正常叠加更高的频率分量,但是这种方法受到了速度精度的制约。Zhang等提出一种基于匹配追踪算法的NMO校正方法^[10],该方法能产生相对不拉伸的结果。然而,由于这种方法是通过移动所有匹配的小波,不同的反射相互干扰,会引起振幅异常及同相轴不连续。Riahi通过修改NMO中的校正轨迹^[11],将地震数据映射到NMO校正的集合中,实现了一种非双曲无拉伸NMO校正方法。但是,这种方法受到动校正过程中近似值和动校正速度误差的影响,并且该过程能够恢复干扰波的反射振幅。

为消除地震数据动校正后的拉伸畸变,提高水平叠加剖面的分辨率,本文提出了一种基于曲波稀疏变换的拉伸畸变消除方法。通过综合模型验证和实际资料处理,验证了本文方法的有效性和准确性。

1 方法原理

1.1 动校正拉伸畸变分析

常规动校正是产生子波拉伸畸变的主要原因之一,它利用NMO速度将不同偏移距反射波传播时间转化为零偏移距反射波传播时间。动校正是一种时间坐标变换,变换后的波形是原始波形的时间畸变和移位^[12]。通过式(1)计算每个点的NMO校正时间:

(1)

Δ t_{NMO} = t_{x} - t_{0} = t_{0} \{{[1 + {(\frac{x}{v t_{0}})}^{2}]}^{1 / 2} - 1\},

其中,t_x为反射波从震源到偏移距为x处的传播时间,t₀为零偏移距反射波传播时间,v是NMO速度。通过计算Δt_NMO,消除偏移距对反射波传播时间的影响。

为了定量分析NMO校正后的频率和振幅变化情况,引入了瞬时频率f(t),瞬时能量E(t,f),瞬时振幅A(f)^[13]。其中瞬时频率的定义如下:

(2)

f (t) = \frac{1}{2 π} \frac{d θ}{d t},

θ为瞬时相位,则偏移距为x和零偏移距处的瞬频率分别为f_x(t_x)= $\frac{1}{2 π}$ $\frac{d θ}{d t_{x}}$ ,f₀(t₀)= $\frac{1}{2 π}$ $\frac{d θ}{d t_{0}}$ 。

令α= $\frac{t_{x}}{t_{0}}$ = ${[\frac{x^{2}}{v^{2} t_{0}^{2}} + 1]}^{1 / 2}$ ,β= ${(\frac{d t_{x}}{d t_{0}})}^{- 1}$ = $\frac{α}{1 - \frac{x^{2} v'}{v^{3} t_{0}}}$ ,其中v是NMO速度,v'=dv/dt₀,由以上关系可以得出动校正后位于偏移距x的瞬时频率f_x(t₀)与零偏移距处的瞬时频率f₀(t₀)的关系:

(3)

f_{0} (t_{0}) = \frac{f_{x} (t_{x})}{β} = \frac{f_{x} (α t_{0})}{β},

经过化简得出如下结果:

(4)

f_{x} (t_{0}) = \frac{α f_{0} (t_{0})}{β} = \frac{v^{3} t_{0} - x^{2} v'}{v^{3} t_{0}} f_{0} (t_{0}) 。

由式(4)可知,经过动校正后位于偏移距x的瞬时频率比零偏移距处的瞬时频率小,偏移距x越大,频率下降得越多。

瞬时频率f(t),瞬时能量E(t,f),瞬时振幅 A(f)存在以下关系:

(5)

\int_{- \infty}^{\infty} E (t, f) d t = A^{2} (f) 。

令γ=f_x/f₀,结合式(5)可以得到零偏移距瞬时振幅和偏移距x处瞬时振幅的关系:

(6)

\begin{array}{r} A_{0} (f_{0}) & = {[\int_{- \infty}^{\infty} E_{0} (t_{0}, f_{0}) d t_{0}]}^{1 / 2} \\ = {[\int_{- \infty}^{\infty} γ^{2} E_{x} (t_{x}, γ f_{0}) d t_{x}]}^{1 / 2} 。 \end{array}

由于γ变化范围较小,通常看作常数,经过近似可以得到如下结果:

(7)

A_{0} (f_{0}) : γ {[\int_{- \infty}^{\infty} γ^{2} E_{x} (t_{x}, γ f_{0}) d t_{x}]}^{1 / 2},

通过简化可得:

(8)

A_{0} (f_{0}) : γ A_{x} (γ f_{0}) 。

经过前面的分析可知,经过动校正后位于偏移距x的瞬时频率比零偏移距处的瞬时频率小,所以γ小于1,动校正后位于偏移距x的瞬时振幅比零偏移距处的瞬时振幅大。

动校正是一种时间坐标变换,变换后的波形相较于原始波形发生了频率下降、振幅增大^[14],这也是动校正中客观存在的现象。

1.2 曲波稀疏变换原理

稀疏性是信号的一个重要特征,由于其对复杂信号和相关问题的分析和处理具有重要影响,广泛应用在压缩感知、图像处理、地球物理数据分析^[15]。

所谓稀疏性是指信号本身或者经过变换后,绝大部分值等于零,仅含有为数不多的非零值。在大多情况下严格的稀疏性很难满足,通常只要信号的多数值接近零,即认定该信号具有稀疏性^[16]。y为长度为N的原始地震信号,Ψ=[ψ₁,ψ₂,…,ψ_N]为稀疏变换矩阵,y满足:

(9)

y = ΨC = \overset{N}{\sum_{i = 1}} c_{i} ψ_{i},

式中:C为信号在变换域的系数向量,即曲波系数C=[c₁,c₂,…,c_i],i=1,2,…,N,其中C中非零元素的个数为‖C‖₀,如果‖C‖₀=K且K≤N,则原始地震信号y是稀疏的。

因为y和C和同一信号在不同域中的等价表示,如果y不稀疏,可以寻找系数向量C稀疏的特定矩阵Ψ,将y转化为稀疏信号。

1.3 基于曲波稀疏变换的拉伸校正

曲波变换是小波变换的一个扩展,具有比小波变换更大的稀疏性^[17],能够获取更好的稀疏结果。曲线变换的这一突出特点,加上其完美的重建和快速的正反变换,使其成为解决地震资料中出现动校拉伸畸变问题的合适工具。

假设地震数据D∈L²(R)满足以下条件:

(10)

D \in R^{M \times N} = [d_{1} | d_{2} | \dots | d_{N}] = S_{x} (D_{0}),

式中:d_i∈R^M是第i道的地震数据,由于动校拉伸和其他因素的影响,不同道之间的数据彼此相对移动,D₀是没有动校拉伸畸变的数据,S_x是一个非线性时移运算符,分别对输入地震数据矩阵的每一列执行操作。下标x∈Z^N表示时移向量(x_i对应于第i道的时移)。可以证明,如果D₀在Ψ域中是稀疏的,则拉伸畸变在该域中表现为非相干噪声的伪影^[18]。因此,拉伸校正可以通过优化曲波域的稀疏最大化来进行求解:

(11)

\dot{x} = \underset{x \in Z^{N}}{argmax} \sum | C^{x} |^{p},

式中:C_x=ΨS_x(D),p>2, $\dot{D}$ = $S_{\dot{x}}$ (D)是D₀的估计值,与通常稀疏正则化中解决向量稀疏性的常用方法不同,式(11)使用系数向量C的p范数(p>2),以增加其稀疏性^[19]。

基于曲波稀疏变换的拉伸校正方法的具体过程如下:给定常规动校正后的地震数据D和曲波稀疏变换矩阵Ψ,假设 $\dot{D}$ =D,k=1并迭代以下步骤:

1)把 ${\dot{D}}^{k - 1}$ 转换成Ψ域:C^k=Ψ ${\dot{D}}^{k - 1}$ ;

2)形成加权矩阵W^k:W^k=|C^k|^p;

3)形成参考数据矩阵:Q^k=Ψ^-¹(W^k.*C^k);

4)将 ${\dot{D}}^{k - 1}$ 的每一列与Q^k的相应列交叉关联,并找到最大关联所对应的索引集合x^k;

5)求取 ${\dot{D}}^{k}$ : ${\dot{D}}^{k}$ = $S_{x^{k}}$ ( ${\dot{D}}^{k - 1}$ );

6)l_p(x^k)=|C^k|⁽^p⁺²⁾,如果| $l_{p}^{k}$ (x^k)- $l_{p}^{k - 1}$ (x^k^-1)|=0,退出;否则k=k+1,转到1)。

当循环结束时, ${\dot{D}}^{k}$ 就是要求取的最终结果,即曲波域稀疏变换的拉伸校正结果。其中(.*)表示逐点乘法,k为迭代次数,曲波系数的稀疏性在每次迭代中都会增加,通过上述步骤,仅经过数次迭代即可获得曲波域稀疏最大化变换结果。曲波稀疏最大化的优势是用最少的信号来恢复原先整个信号,经过动校正后的地震数据,有效信号占主体,因此在曲波稀疏域中,拉伸畸变部分变得极为容易校正,极大地提高了求解速度和精度。由于拉伸畸变在曲波稀疏最大化域中表现为非相干噪声的伪影,在校正过程中主要是通过去除非相干噪声的伪影来实现拉伸校正,因此不会存在校正过量的情况,当非相干噪声的伪影去除不完全时,可能会存在校正不足的情况。

2 模型数据测试

2.1 单界面模型

建立一个两层水平层状介质模型一, 该模型参数如表1所示,采用主频为45 Hz的雷克子波,使用Shuey推导的Zoeppritz近似方程进行正演获得,如图1a所示。

表1 模型一层状介质参数

Table 1 Model 1 layered media parameters

层位	纵波速度v_p /(m·s^-1)	横波速度v_s /(m·s^-1)	密度ρ /(g·cm^-3)
1	3500	2500	2.0
2	4000	3000	2.5

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

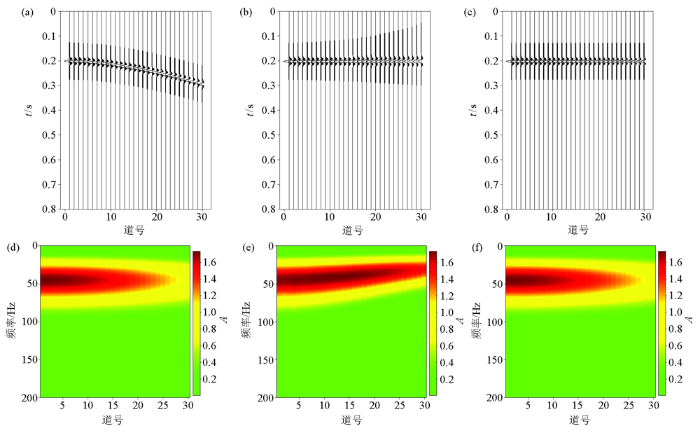
图1 测试模型一

a—合成地震记录;b—常规动校正结果;c—曲波稀疏拉伸校正结果;d—原始地震记录振幅谱;e—动校正结果振幅谱;f—本文方法拉伸校正结果振幅谱

Fig.1 Test model 1

a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of the original seismic record;e—amplitude spectrum of NMO;f—amplitude spectrum of the tensile correction results by the method presented in this paper

如图1b所示,经过常规动校正后,远偏移距的地震同相轴相对于近偏移距的明显变宽,从动校正后的振幅谱可以看出(图1e),随着偏移距的不断增大,频率逐渐降低,振幅不断增大,即产生了因子波拉伸所致的频率降低和振幅扩大问题,与上文中动校正拉伸畸变分析的结果一致。而经过曲波稀疏拉伸校正处理后,如图1c所示,同相轴被校平,远偏移距处的振幅增大现象得到消除。同时,地震道集的振幅谱(图1f)和原始地震道集的振幅谱(图1d)一致,每道的主频基本都保持在 45 Hz 不变,而且完全保留了原始地震道集振幅随炮检距的变化信息,有很好的保幅效果。本文方法能够校正动校拉伸引起的振幅增大和频率降低问题,因此,该方法对消除动校拉伸现象有很好的适应性。

2.2 多界面模型(无同相轴交叉)

2.2.1 无随机噪声

建立一个四层水平层状介质模型二,其参数如表2所示,采用10 m的道间距,使用主频为30 Hz的雷克子波进行正演获得,结果如图2a所示。

表2 模型二层状介质参数

Table 2 Model 2 layered media parameters

层位	速度v/(m·s^-1)	密度ρ/(g·cm^-3)
1	3500	1.3
2	4000	1.5
3	5000	2.0
4	5500	2.2

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 测试模型二(不含随机噪声)

a—合成地震记录;b—常规动校正结果;c—曲波稀疏拉伸校正结果;d—动校正结果振幅谱;e—本文方法拉伸校正结果振幅谱

Fig.2 Test model 2(no random noise)

a—synthetic seismogram;b—conventional NMO correction results;c—curvelet sparse stretch correction;d—amplitude spectrum of NMO;e—amplitude spectrum of the tensile correction results by the method presented in this paper

经过常规动校正处理得到如图2b所示的结果,可以明显看到上方两条同相轴没有被拉平,随着偏移距逐渐增大,同相轴逐步变宽,畸变增大。通过以上比较,经过动校正后,上层和远偏移距处的拉伸畸变较大。图2c是采用本文方法对图2b进行的拉伸校正结果,可以看出3个同相轴均已校平且没有出现畸变,远近偏移距同相轴宽度及振幅大小一致。

图2d是根据动校正之后(图2b)获取的振幅谱,从图中可以看出,40道之后的频率由高频逐步向低频进行转变,图2d中的频率变化越大,图2b中同相轴拉伸畸变效应就越明显。图2e是根据拉伸校正结果(图2c)获取的振幅谱,从图中可以看出,远近偏移距的主频没有发生变化,始终保持在30 Hz。曲波稀疏拉伸校正结果振幅谱中显示出远近道的主频率均为30 Hz,振幅大小几乎一致,频率带宽相同,高频信息得以恢复。

2.2.2 含有随机噪声

为了测试随机噪声对本文方法的影响,在图 2a所示的模型数据中加入随机噪声,得到图3a所示的模型,用以验证本文方法的正确性。经过常规动校正处理得到如图3b所示的结果,可以明显看到同相轴发生拉伸畸变,且随机噪声并未得到消除。图3c是采用本文方法对图3b进行的拉伸校正结果,同相轴出现拉伸畸变的部位基本被消除,远近偏移距同相轴宽度以及振幅大小一致,随机噪声得到压制。

图3

新窗口打开| 下载原图ZIP| 生成PPT

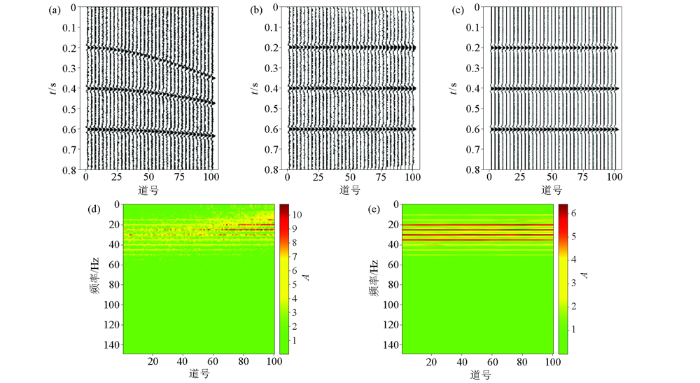
图3 测试模型二(含随机噪声)

a—合成地震记录;b—常规动校正结果;c—曲波稀疏拉伸校正结果;d—原始地震记录振幅谱;e—动校正结果振幅谱;f—本文方法拉伸校正结果振幅谱

Fig.3 Test model 2(containing random noise)

图3d是根据动校正之后(图3b)获取的振幅谱,从图中可以看出, 振幅和频率变化趋势与未加噪的振幅谱几乎一致,由于随机噪声的影响,振幅谱中出现了许多噪点。图3e是根据拉伸校正结果(图3c)获取的振幅谱,从图中可以看出,校正结果振幅谱中显示出远近道的主频率相同,振幅大小一致,频率带宽相同,高频信息得以恢复,并且图3d中的噪点得到消除。

常规动校正受随机噪声影响较大,并不能消除随机噪声带来的影响,经过模型验证,本文提出的曲波稀疏拉伸校正方法不仅能够消除由动校正带来的拉伸畸变,而且能够压制随机噪声。这是由于地震信号在曲波稀疏域内是稀疏的,仅通过少量的大系数就能够近似表示有效地震信号,而随机噪声在曲波稀疏域内表现为小系数。在稀疏最大化的原则下,仅通过保留少量的大系数进行重建地震信号,从而去除随机噪声的干扰。

2.3 多界面模型(同相轴交叉)

在复杂地质条件下,由于深层界面的反射波旅行时小于浅层反射波旅行,会产生同相轴交叉现象。本文构造如图3a所示的同相轴交叉模型三,其参数如表3所示,采用25 m的道间距,使用主频为30 Hz的雷克子波进行正演获得。通过利用本文方法,校正存在于同相轴交叉情形下的动校正拉伸畸变,验证本文方法在同相轴交叉情况下的适用性。

表3 模型三水平层状介质参数

Table 3 Model 3 layered media parameters

层位	速度v/(m·s^-1)	密度ρ/(g·cm^-3)
1	4000	1.6
2	6000	2.2
3	5000	1.8
4	5500	2.0

新窗口打开| 下载CSV

图4b是模型三数据常规动校正结果,从图中可以看出,交叉的两条同相轴在交叉点附近发生严重的拉伸畸变,两条同相轴发生信息混叠,十分混乱。经过曲波稀疏变换拉伸校正处理后(图 4c),交叉点附近的同相轴拉伸畸变得到消除,使得动校正后的同相轴能够真实反映地下介质情况。

图4

新窗口打开| 下载原图ZIP| 生成PPT

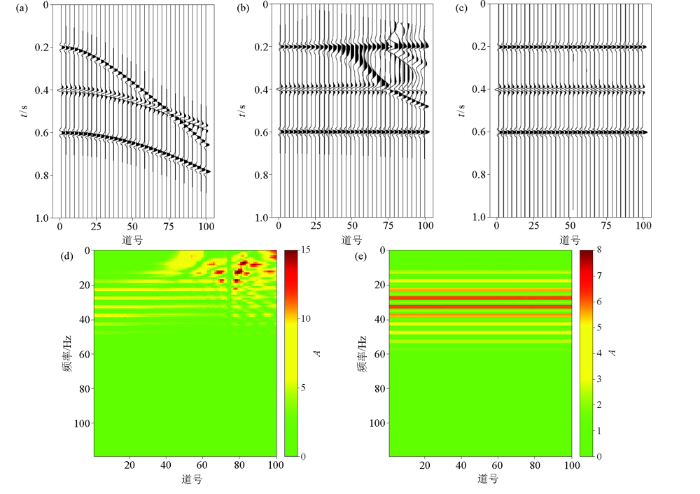
图4 测试模型三

a—合成地震记录;b—常规动校正结果;c—曲波稀疏拉伸校正结果;d—动校正结果振幅谱;e—本文方法拉伸校正结果振幅谱

Fig.4 Test model 3

图4d是根据动校正之后(图4b)获取的振幅谱,通过且在交叉点处有一条贯穿低频到高频的线。图4e是利用本文方法对动校正后的数据进行拉伸校正后得到的振幅谱,从图中可以看到各道数据没有发生频率范围移动的现象,主频保持在30 Hz。

通过以上的对比研究,表明了该方法可以很好地适用于含有存在同相轴交叉现象的拉伸校正。

3 叠前数据处理

为了验证本文方法的有效性与准确性,对我国南部某地区地震数据进行测试。该地震数据总共100个CRP道集,每道覆盖60次,道间距为100 m、采样率为2 ms。

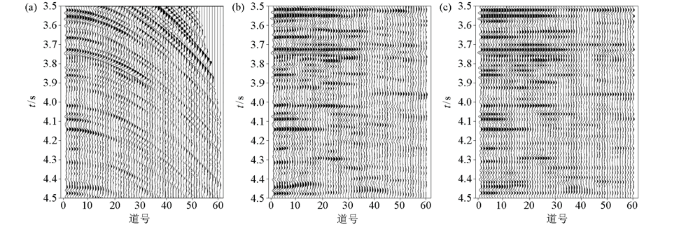
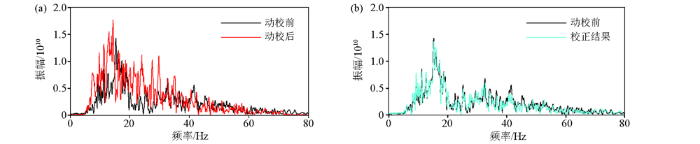
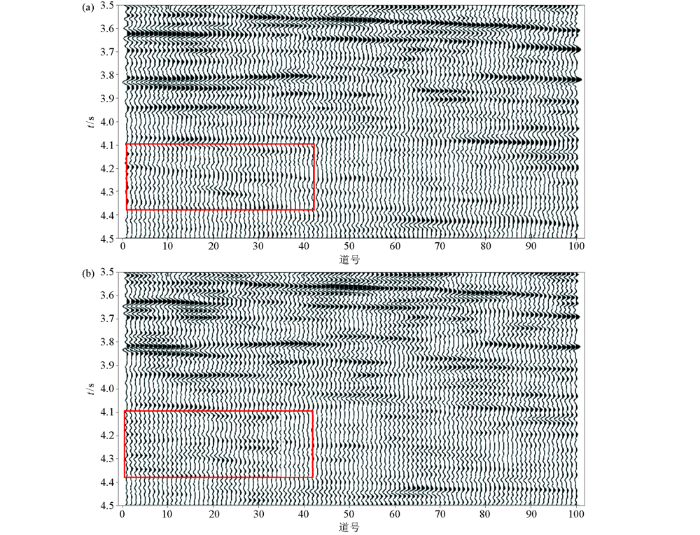
如图5b是一个CRP道集经过常规动校正后得到的结果,从常规动校正的结果中可以看出叠前CRP道集中同相轴基本被校平,但是在某些区域发生严重畸变,例如在远偏移距处,同相轴出现分叉、断裂以及消失的情况。图5c是应用本文方法进行拉伸校正的结果,如图所示,出现拉伸畸变的地方均被校正,同相轴的横向连续性得到恢复。在图6a中给出了原始CRP道集和常规动校正后的远偏移距处的频谱对比图,从图中可以看出,经过动校正后远偏移距处出现振幅增强和主频降低的现象,与上文中的模型结果一致,这意味着远偏移距处由于动校正拉伸畸变效应而缺失了高频信息。在图6b中给出了原始CRP道集和曲波稀疏拉伸校正后的远偏移距处的频谱对比图,图中显示出校正后的远偏移距的主频和振幅和原始CRP道集的基本保持一致,频率带宽相同,高频信息得以恢复。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 实际地震资料处理结果

a—原始CRP道集;b—常规动校正结果;c—曲波稀疏拉伸动校正结果

Fig.5 Actual seismic data processing results

a—original CRP gathers;b—conventional NMO correction results;c—curvelet sparse stretch correction

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 拉伸校正前后频谱对比

a—远道原始CRP道集和动校正结果频谱对比;b—远道原始CRP道集和曲波稀疏拉伸校正结果频谱对比

Fig.6 Spectrum comparison before and after stretch correction

a—spectrum comparison between original CRP gathers and NMO correction results for long distance;b—spectrum comparison of original CRP gathers and curve sparse stretch correction results for long distance

对常规动校正处理后的CRP道集和曲波稀疏拉伸校正后的CRP道集分别进行叠加处理,得到了如图7所示的叠加剖面。图7a为常规动校正后的叠加剖面,受到拉伸畸变的影响,引起非同相叠加,因此导致叠加剖面的同相轴连续性较差且整体分辨率下降。对比红框内的研究区域,可以看出通过曲波稀疏变换拉伸校正后的叠加剖面分辨率得到显著提高,一些能量较弱的同相轴在经过拉伸校正后,能量得到明显增强,这是由于叠加之前的CRP道集同相轴拉伸畸变部分得到消除,将校正后的叠加转变为同向叠加,使得叠后同相轴的能量得到增强、连续性得到提升。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 叠加剖面

a—常规动校正叠加剖面;b—曲波稀疏拉伸校正叠加剖面

Fig.7 Stacked section

a—conventional NMO correction stack section;b—curvelet sparse stretch correction stack section

4 结论

本文分析了地震资料处理中常规动校正产生拉伸畸变的原因,明确拉伸畸变是常规动校正的固有特性,并在曲波稀疏性最大化的框架下,进行了拉伸校正。文中将拉伸校正描述为一个非线性优化问题,提出了一种保证收敛性的高效迭代算法来求解生成的非线性优化问题,该方法能在较少的迭代次数内快速收敛,实现拉伸校正。应用本文方法进行拉伸校正具有以下优势:首先,曲波域本身具有较大的稀疏性,应用上文中提出的算法,能够快速得到曲波域稀疏最大化结果,大大提高了计算效率;其次,拉伸校正后,保留了原始地震道集振幅随炮检距的变化信息,有很好的保幅效果;最后,本文方法能够校平同相轴,实现同相叠加,显著提高了叠加剖面的分辨率。将该方法应用于各种合成地震记录和实际叠前地震资料中,实验证明,曲波稀疏拉伸校正方法是解决拉伸校正问题的一种非常有效的方法。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

夏洪瑞, 葛川庆, 邹少峰.

动校拉伸现象分析及其消除

[J]. 石油物探, 2005,44(3):220-224.

[本文引用: 1]

Xia H

, Ge C

, Zou S

Analysis and elimination of stretch phenomenon in dynamic school

[J]. Geophysical Prospecting for Petroleum, 2005,44(3):220-224.

[本文引用: 1]

[2]

赵小龙, 吴国忱.

基于非稳态匹配的角度域叠前道集去调谐方法

[J]. 物探与化探, 2017,41(1):141-146.

[本文引用: 1]

Zhao X

, Wu G

Angle domain prestack gather detuning method based on unsteady matching

[J]. Geophysical and Geochemical Exploration, 2017,41(1):141-146.

[本文引用: 1]

[3]

孙成禹, 谢俊法, 闫月锋.

一种无拉伸畸变的动校正方法

[J]. 石油物探, 2016,55(5):664-673.

[本文引用: 1]

Sun C

, Xie J

, Yan Y

A dynamic correction method without stretching distortion

[J]. Geophysical Prospecting for Petroleum, 2016,55(5):664-673.

[本文引用: 1]

[4]

Rupert G

, Chun J

The block move sum normal moveout correction

[J]. Geophysics, 1975,40(1):17-24.

DOI:10.1190/1.1440511 URL [本文引用: 1]

[5]

Shatilo

, Aminzadeh

Constant normal-moveout (CNMO) correction: a technique and test results

[J]. Geophysical Prospecting, 2000: 48.

[本文引用: 1]

[6]

Hicks G

Removing NMO stretch using the Radon and Fourier-Radon transforms

[C]//63^rd EAGE Conference & Exhibition, 2001.

[本文引用: 1]

[7]

Trickett

Stretch-free stacking

[C]//73^rd Annual International Meeting,SEG,Expanded Abstracts, 1949: 4645.

[本文引用: 1]

[8]

崔宝文, 王维红.

频谱代换无拉伸动校正方法研究

[J]. 地球物理学进展, 2007,22(3):960-965.

[本文引用: 1]

Cui B

, Wang W

Study on spectrum substitution non stretching NMO method

[J]. Progress in Geophysics, 2007,22(3):960-965.

[本文引用: 1]

[9]

Kazemi

, Siahkoohi H

Local stretch zeroing NMO correction

[J]. Geophysical Journal International, 2014,188(1):123-130.

DOI:10.1111/gji.2012.188.issue-1 URL [本文引用: 1]

[10]

Zhang

, Zhang

, Guo

, et al.

Nonstretching NMO correction of prestack time-migrated gathers using a matching-pursuit algorithm

[J]. Geophysics, 2013,78(1):U9-U18.

DOI:10.1190/geo2011-0509.1 URL [本文引用: 1]

[11]

Abedi M

, Riahi M

Nonhyperbolic stretch-free normal moveout correction

[J]. Geophysics, 2016,81(6):U87-U95.

DOI:10.1190/geo2016-0078.1 URL [本文引用: 1]

[12]

Zhang

, Lan

Seismic gather wavelet stretching correction based on multi-wavelet decomposition algorithm

[J]. Geophysics, 2020,85(5):1-33.

DOI:10.1190/geo2018-0881.1 URL [本文引用: 1]

[13]

Barnes A

Another look at NMO stretch

[J]. Geophysics, 2012,57(5):749.

DOI:10.1190/1.1443289 URL [本文引用: 1]

[14]

Buchholtz

A note on signal distortion due to dynamic (NMO) corrections

[J]. Geophysical Prospecting, 1972,20(2):395-402.

DOI:10.1111/gpr.1972.20.issue-2 URL [本文引用: 1]

[15]

Candes

, Romberg

, Tao

Stable signal recovery from incomplete and inaccurate measurements

[J]. Comm. Pure Appl. Math., 2005,59(8):1-15.

DOI:10.1002/(ISSN)1097-0312 URL [本文引用: 1]

[16]

罗勇, 毛海波, 杨晓海, 等.

基于双重稀疏表示的地震资料随机噪声衰减方法

[J]. 物探与化探, 2018,42(3):608-615.

[本文引用: 1]

Luo

, Mao H

, Yang X

, et al.

Random noise attenuation method for seismic data based on double sparse representation

[J]. Geophysical and Geochemical Exploration, 2018,42(3):608-615.

[本文引用: 1]

[17]

Herrmann F

, Moghaddam

, Stolk C

Sparsity- and continuity-promoting seismic image recovery with curvelet frames

[J]. Applied & Computational Harmonic Analysis, 2008,24(2):150-173.

[本文引用: 1]

[18]

Gholami

Residual statics estimation by sparsity maximization

[J]. Geophysics, 2013,78(1):V11-V19.

DOI:10.1190/geo2012-0035.1 URL [本文引用: 1]

[19]

Gholami

, Hosseini S

A general framework for sparsity based denoising and inversion

[J]. IEEE Transactions on Signal Processing, 2011,59(11):5202-5211.

DOI:10.1109/TSP.2011.2164074 URL [本文引用: 1]

动校拉伸现象分析及其消除

2005

... 动校正是地震数据处理中的重要一环,动校正的结果直接影响水平叠加、AVO分析、反演等后续处理过程^[1].但是,常规动校正由于其固有的特性,动校正之后的同相轴会存在没有被校平的情况,产生较为复杂的拉伸畸变效应,一般表现为远偏移距处的频率降低、振幅变大^[2].对于畸变严重的部分,通常采用切除的方法来降低畸变的影响.然而,切除的部分缩短了有效扩展长度、降低了覆盖次数,从而降低了叠加剖面的分辨率^[3]. ...

动校拉伸现象分析及其消除

2005

基于非稳态匹配的角度域叠前道集去调谐方法

2017

基于非稳态匹配的角度域叠前道集去调谐方法

2017

一种无拉伸畸变的动校正方法

2016

一种无拉伸畸变的动校正方法

2016

The block move sum normal moveout correction

1975

... Rupert和Chun提出了整体搬家(bock move sum,BMS)方法^[4],在BMS方法中,小时间窗口中的地震数据可以实现数据的块移动,避免在每个点上出现不同的校正值而引起拉伸畸变.然而,在BMS中数据块的大小需要与小波周期相同,并且在块边界上会发生不连续的现象.Shatilo和Aminzadeh提出了一种固定时差动校正(constant normal move out,CNMO)^[5],CNMO方法与传统逐点搬家动校正方法有着明显的区别,那就是在一个固定的时窗内对所有的地震道按照走时公式采用了固定的时差常数来校平CMP道集上的反射同相轴,这种方法校正后的数据分辨率更高,从而避免了大孔径处信号的频率失真,在一定程度上保留了更多的长偏移距信号,CNMO的缺陷是在长偏移距处产生了假同相轴.Hicks在叠加过程中使用抛物线Radon变换来消除NMO拉伸畸变^[6].然而,该方法在存在噪声的情况下是不稳定的,并且不能有效地校正振幅较弱的区域.Trickett开发了一种无拉伸叠加方法^[7],将NMO校正和叠加两步替换为零偏移叠加的单步反演,该方法将BMS技术应用于反演,降低了相邻块间不连续性.崔宝文等通过傅里叶变换,把时间偏移距域地震数据转化为频率域,将远偏移距的频谱替换为近偏移距的频谱^[8],避免了拉伸,但存在相互干扰的情况.Kazemi和Siahkoohi提出一种避免NMO拉伸的局部拉伸调零方法^[9],根据速度分析的结果,将数据分成不同的时间块.该方法消除了产生NMO拉伸的插值数据样本的理论曲线,从而保留了一般比正常叠加更高的频率分量,但是这种方法受到了速度精度的制约.Zhang等提出一种基于匹配追踪算法的NMO校正方法^[10],该方法能产生相对不拉伸的结果.然而,由于这种方法是通过移动所有匹配的小波,不同的反射相互干扰,会引起振幅异常及同相轴不连续.Riahi通过修改NMO中的校正轨迹^[11],将地震数据映射到NMO校正的集合中,实现了一种非双曲无拉伸NMO校正方法.但是,这种方法受到动校正过程中近似值和动校正速度误差的影响,并且该过程能够恢复干扰波的反射振幅. ...

Constant normal-moveout (CNMO) correction: a technique and test results

2000

Removing NMO stretch using the Radon and Fourier-Radon transforms

2001

Stretch-free stacking

1949

频谱代换无拉伸动校正方法研究

2007

频谱代换无拉伸动校正方法研究

2007

Local stretch zeroing NMO correction

2014

Nonstretching NMO correction of prestack time-migrated gathers using a matching-pursuit algorithm

2013

Nonhyperbolic stretch-free normal moveout correction

2016

Seismic gather wavelet stretching correction based on multi-wavelet decomposition algorithm

2020

... 常规动校正是产生子波拉伸畸变的主要原因之一,它利用NMO速度将不同偏移距反射波传播时间转化为零偏移距反射波传播时间.动校正是一种时间坐标变换,变换后的波形是原始波形的时间畸变和移位^[12].通过式(1)计算每个点的NMO校正时间: ...

Another look at NMO stretch

2012

... 为了定量分析NMO校正后的频率和振幅变化情况,引入了瞬时频率f(t),瞬时能量E(t,f),瞬时振幅A(f)^[13].其中瞬时频率的定义如下: ...

A note on signal distortion due to dynamic (NMO) corrections

1972

... 动校正是一种时间坐标变换,变换后的波形相较于原始波形发生了频率下降、振幅增大^[14],这也是动校正中客观存在的现象. ...

Stable signal recovery from incomplete and inaccurate measurements

2005

... 稀疏性是信号的一个重要特征,由于其对复杂信号和相关问题的分析和处理具有重要影响,广泛应用在压缩感知、图像处理、地球物理数据分析^[15]. ...

基于双重稀疏表示的地震资料随机噪声衰减方法

2018

... 所谓稀疏性是指信号本身或者经过变换后,绝大部分值等于零,仅含有为数不多的非零值.在大多情况下严格的稀疏性很难满足,通常只要信号的多数值接近零,即认定该信号具有稀疏性^[16].y为长度为N的原始地震信号,Ψ=[ψ₁,ψ₂,…,ψ_N]为稀疏变换矩阵,y满足: ...

基于双重稀疏表示的地震资料随机噪声衰减方法

2018

Sparsity- and continuity-promoting seismic image recovery with curvelet frames

2008

... 曲波变换是小波变换的一个扩展,具有比小波变换更大的稀疏性^[17],能够获取更好的稀疏结果.曲线变换的这一突出特点,加上其完美的重建和快速的正反变换,使其成为解决地震资料中出现动校拉伸畸变问题的合适工具. ...

Residual statics estimation by sparsity maximization

2013

... 式中:d_i∈R^M是第i道的地震数据,由于动校拉伸和其他因素的影响,不同道之间的数据彼此相对移动,D₀是没有动校拉伸畸变的数据,S_x是一个非线性时移运算符,分别对输入地震数据矩阵的每一列执行操作.下标x∈Z^N表示时移向量(x_i对应于第i道的时移).可以证明,如果D₀在Ψ域中是稀疏的,则拉伸畸变在该域中表现为非相干噪声的伪影^[18].因此,拉伸校正可以通过优化曲波域的稀疏最大化来进行求解: ...

A general framework for sparsity based denoising and inversion

2011

... 式中:C_x=ΨS_x(D),p>2,

\dot{D}

S_{\dot{x}}

(D)是D₀的估计值,与通常稀疏正则化中解决向量稀疏性的常用方法不同,式(11)使用系数向量C的p范数(p>2),以增加其稀疏性^[19]. ...

〈

〉