基于归一化磁源强度垂向差分的磁源参数快速估计方法

doi:10.11720/wtyht.2021.0291

基于归一化磁源强度垂向差分的磁源参数快速估计方法

黄远生^,¹^,², 王彦国^,¹, 罗潇³

1.东华理工大学地球物理与测控技术学院,江西南昌 330013

2.海南水文地质工程地质勘察院,海南海口 571100

3.核工业230研究所,湖南长沙 410011

A fast estimation method of magnetic-source parameters based on the vertical difference of normalized source strength

HUANG Yuan-Sheng^,¹^,², WANG Yan-Guo^,¹, LUO Xiao³

1. School of Geophysics and Measure-control Technology, East China University of Technology, Nanchang 330013, China

2. Hainan Investigation Institute of Hydrogeology and Engineering Geology, Haikou 571100, China

3. No. 230 Research Institute of Nuclear Industry, Changsha 410011, China

通讯作者: 王彦国(1985-),男,博士,副教授,硕士研究生导师,从事勘探重磁学方面的教学与研究工作。Email:wangyg8503@126.com

责任编辑: 王萌

收稿日期: 2021-02-9 修回日期: 2021-05-19

基金资助:

国家重点研发计划项目“铀矿基地深部成矿条件地球物理探测技术研究”.  2017YFC0602603
江西省自然科学基金项目“基于位场多源型tilt-depth法的场源深度快速自动反演研究”.  20171BAB213030
国家自然科学基金项目“基于位场广义梯度张量的欧拉反褶积方法研究”.  41504098

Received: 2021-02-9 Revised: 2021-05-19

作者简介 About authors

黄远生(1994-),男,在读硕士研究生,主要从事重磁勘探方面的学习与研究工作。Email: 1289418554@qq.com

摘要

磁异常快速自动反演是磁数据解释的主要手段,归一化磁源强度因不受磁化方向影响而成为三维磁数据解释的主要方法。本文在归一化磁源强度基础上,首先进行了不同高度上的垂向差分计算,再根据不同高度差分关系,推导出了一种基于归一化磁源强度垂向差分的磁源参数快速反演方法。该方法可通过调节延拓高度来提高计算稳定性。模型试验表明归一化磁源强度垂向差分具有更高的异常分辨率,极大值能够有效地识别场源水平位置,而快速反演方法则较好地获取了场源的深度与构造指数。将本文方法应用于内蒙古M区地面磁异常之中,获得了磁源的平面展布和深度及构造指数信息,为研究区隐伏岩体分布提供了依据。

关键词： 归一化磁源强度 ; 磁化方向 ; 垂向差分 ; 磁源 ; 参数反演

Abstract

Fast automatic inversion is a primary tool for magnetic data interpretation. The normalized source strength (NSS) is one main method for three-dimensional magnetic data interpretation as it is independent of magnetization direction. In this paper, the vertical difference of the normalized source of strength is introduced, and a fast estimation method of magnetic-source parameters based on the vertical difference of normalized source strength is derived in the light of the vertical difference of NSS at different height. In addition, upward continuation of suitable height can be used to improve the stability of the method. Model tests shows that the vertical difference of NSS has higher resolution ability and can recognize the horizontal locations of magnetic sources, and the proposed automatic inversion method can obtain the depths and structural indices of the sources. In this paper, the proposed method is applied to magnetic anomaly of M area over Inner Mongolia, and obtain the horizontal locations, depths and structural indices of magnetic sources. The results could provide useful information for forecasting the distribution of concealed rock mass.

Keywords： normalized source strength ; magnetization direction ; vertical difference ; magnetic source ; parameter inversion

PDF (5303KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄远生, 王彦国, 罗潇. 基于归一化磁源强度垂向差分的磁源参数快速估计方法. 物探与化探[J], 2021, 45(6): 1588-1596 doi:10.11720/wtyht.2021.0291

HUANG Yuan-Sheng, WANG Yan-Guo, LUO Xiao. A fast estimation method of magnetic-source parameters based on the vertical difference of normalized source strength. Geophysical and Geochemical Exploration[J], 2021, 45(6): 1588-1596 doi:10.11720/wtyht.2021.0291

0 引言

磁异常快速反演一直是磁法数据处理与解释的研究重点与热点,该类方法能够在无先验信息约束下快速获取场源的位置与几何参数。目前较为常用的快速反演方法有欧拉反褶积法、解析信号法、tilt-depth法等。欧拉反褶积是Peters^[1]提出的,Thompson^[2]推导了二维欧拉反褶积,Reid 等^[3]将其推广至三维。张量欧拉反褶积^[4]扩展了欧拉方程个数,提高了反演解收敛性;Huang 等^[5]证明了位场解析信号同样满足欧拉齐次方程;AN-EUL 法^[6]能够快速估算场源深度与构造指数; Tilt-Euler 法^[7]无需已知场源构造指数,避免了因构造指数选取不当导致反演解发散的问题;张量局部波数的欧拉反褶积法^[8]进一步扩展了方程组个数,获得了良好的应用效果。不过欧拉反褶积及其改进方法的反演解中存在大量的虚假解,需要建立有效的筛选机制,另外背景场、噪声干扰及窗口大小选择也会对反演结果产生一定影响。二维磁解析信号振幅不受磁化方向影响^[9],Macleod ^[10]推导出了二维磁解析信号振幅的通用表达式;Salem 等^[11]在解析信号及其水平总梯度基础上采用线性最小二乘法计算磁源深度及构造指数;Salem 等^[12]又根据解析信号及磁异常垂向导数解析信号关系进行磁源参数估计;Ma 和Du^[13]在解析信号振幅的解析信号与解析信号比值基础上提出了改进解析信号来实现单一场源深度及构造指数的估算;Cooper^[14,15]同样采用不同阶次解析信号来估计岩脉及台阶的深度;Cooper 和Whitehead^[16]利用不同阶次解析信号比值进行场源深度估算,不过改进方法不需要已知构造指数;Cooper^[17]又采用了解析信号对数实现磁源深度估计工作。Wang等^[18]采用解析信号及其倒数进行磁源参数反演计算,对深部场源反演效果较好。但三维解析信号在一定程度上受磁化角度影响,在三维磁异常反演中使用较小。Tilt-depth 法可用于快速估算场源上顶深度,该方法是由Salem 等^[19]在Tilt 梯度及磁场通用梯度公式进行理论推导而来; Fairhead 等^[20]提出了基于化极与化赤相结合的tilt-depth 法,还可以实现场源磁化率估计;张恒磊等^[21]提出了基于二阶导数的磁源边界与顶部深度快速反演方法,有效地消除了区域场对反演结果的影响; Wang 等^[22]提出了改进tilt-depth 法来估计磁源的上顶与下底深度,并采用多特征点联合计算来提高反演解的可靠性;Cooper ^[23]在Hilbert 变换基础上推导出了岩脉模型的垂直磁化磁位的tilt-depth 公式,提高了方法实用性及稳定性;曹伟平等^[24]对tilt-depth 法进行了深入研究,指出了该方法并不适用于埋深大、水平尺度小的磁源深度反演计算。由于tilt-depth 法及改进算法均需要在化极或化赤基础上完成计算,因此并不能直接用于斜磁化磁源深度的估算。

归一化磁源强度是在磁梯度张量特征值基础上提出的,该方法不(少)受磁化方向影响,是三维磁异常解释的常用工具。Wilson^[25]首先给出了磁偶极子下归一化磁源强度的表达式,Beiki等^[26]给出了归一化磁源强度的通用表达形式,建立了归一化磁源强度与场源位置、构造指数的关系,同时结合欧拉反褶积实现了三维磁源的位置及构造指数反演;Pikington 和Beiki^[27]在归一化磁源强度基础上实现了剩磁情况下的磁源空间位置及磁化率反演;Guo等^[28] 将归一化磁源强度与相关成像结合来反映地下磁性体的三维空间展布状态;饶椿锋等^[29]将归一化磁源强度与正则化共轭梯度法结合来反演磁源的磁化率。本文在归一化磁源强度垂向差分基础上,提出了一种场源快速反演方法,并进行了模型分析与实例应用。

1 基本原理

对于体积为V,磁化强度为M的磁性体,其磁位U的表达式^[30]为:

(1)$U=-\frac{1}{4 \pi} \int_{v} M\left(r_{0}\right) \cdot \nabla\left(\frac{1}{\left|r-r_{0}\right|}\right) \mathrm{d} v$

式中:|r-r₀|是观测点到场源点的距离。

磁梯度张量^[31]可以表示为:

(2)

Γ = μ_{0} [\begin{array}{l} \frac{\partial^{2} U}{\partial x^{2}} & \frac{\partial^{2} U}{\partial x \partial y} & \frac{\partial^{2} U}{\partial x \partial z} \\ \frac{\partial^{2} U}{\partial y \partial x} & \frac{\partial^{2} U}{\partial y^{2}} & \frac{\partial^{2} U}{\partial y \partial z} \\ \frac{\partial^{2} U}{\partial z \partial x} & \frac{\partial^{2} U}{\partial z \partial y} & \frac{\partial^{2} U}{\partial z^{2}} \end{array}] = [\begin{array}{l} \frac{\partial B_{x}}{\partial x} & \frac{\partial B_{x}}{\partial y} & \frac{\partial B_{x}}{\partial z} \\ \frac{\partial B_{y}}{\partial x} & \frac{\partial B_{y}}{\partial y} & \frac{\partial B_{y}}{\partial z} \\ \frac{\partial B_{z}}{\partial x} & \frac{\partial B_{z}}{\partial y} & \frac{\partial B_{z}}{\partial z} \end{array}]

式中:μ₀为真空磁导率;B_x、B_y、B_z是磁场B的x、y、z这3个方向分量。对梯度张量Γ进行对角化处理,得:

(3)

Γ = L^{T} ΛL = [l_{1} l_{2} l_{3}]^{T} [\begin{array}{l} λ_{1} & 0 & 0 \\ 0 & λ_{2} & 0 \\ 0 & 0 & λ_{3} \end{array}] [l_{1} l_{2} l_{3}],

式中:l₁、l₂和l₃为Γ的特征向量;λ₁、λ₂、λ₃为对应的特征值。Wilson^[25]给出磁偶极子的归一化磁源强度μ的定义,并推导出梯度张量特征值表达式:

(4)

μ = \sqrt[]{- λ_{2}^{2} - λ_{1} λ_{2}},

Beiki等^[26]给出了归一化磁源强度的统一表达式:

(5)

μ = \frac{α}{[(x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2}]^{(N + 1) / 2}}

式中:α是与磁化强度有关的物理量;(x,y,z)和(x₀,y₀,z₀)分别是观测点与场源点坐标;N为构造指数,与磁源几何形状有关,当N=0,1,2,3时,分别对应台阶、岩脉、圆柱体及球体。

当Δz→0,对于两个不同高度z₁,z₂,有:

(6)

Δ μ_{1} = μ (x, y, z_{1}) - μ (x, y, z_{1} + Δ z) ≅ \frac{\partial μ}{\partial z_{1}} Δ z = \frac{α (N + 1) (z_{0} - z_{1}) Δ z}{[(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{1} - z_{0})^{2}]^{(N + 3) / 2}}

(7)

\begin{array}{l} Δ μ_{2} = μ (x, y, z_{2}) - μ (x, y, z_{2} + Δ z) ≅ \frac{\partial μ}{\partial z_{2}} Δ z = \frac{α (N + 1) (z_{0} - z_{2}) Δ z}{[(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{2} - z_{0})^{2}]^{(N + 3) / 2}} \end{array}

分别将式(6)、(7)对式(5)做比值,得:

(8)

k_{1} = \frac{Δ μ_{1}}{μ_{1}} = \frac{μ (x, y, z_{1}) - μ (x, y, z_{1} + Δ z)}{μ (x, y, z_{1})} = \frac{(N + 1) (z_{0} - z_{1}) Δ z}{[(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{1} - z_{0})^{2}]},

(9)

k_{2} = \frac{Δ μ_{2}}{μ_{2}} = \frac{μ (x, y, z_{2}) - μ (x, y, z_{2} + Δ z)}{μ (x, y, z_{2})} = \frac{(N + 1) (z_{0} - z_{2}) Δ z}{[(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{2} - z_{0})^{2}]},

(10)

k_{1} / k_{2} 得 : \frac{k_{1}}{k_{2}} = \frac{(z_{0} - z_{1}) [(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{0} - z_{2})^{2}]}{(z_{0} - z_{2}) [(x - x_{0})^{2} + (y - y_{0})^{2} + (z_{0} - z_{1})^{2}]}

当x→x₀,y→y₀时:

(11)

{\frac{k_{1}}{k_{2}}|}_{x \to x_{0}, y \to y_{0}} = \frac{z_{0} - z_{2}}{z_{0} - z_{1}}

则磁源深度z₀可表示为:

(12)

z_{0} = {\frac{k_{1} z_{1} - k_{2} z_{2}}{k_{1} - k_{2}}|}_{x \to x_{0}, y \to y_{0}}

将z₀表达式带入式(8)或(9),可求得构造指数N:

(13)

N = {[k_{1} k_{2} \frac{z_{1} - z_{2}}{(k_{1} - k_{2}) Δ z} - 1]|}_{x \to x_{0}, y \to y_{0}}

显然,估计场源深度z₀和构造指数N,需要事先给定场源的水平位置(x₀,y₀),Δz取值以及z₁、z₂的大小。由于归一化磁源强度的垂向差分极大值对应着场源水平位置,因此场源的水平坐标(x₀,y₀)则看作是归一化磁源强度垂向差分(Δμ₁)极大值位置;Δz不易过大,一般取0.05~0.2倍点距,否则式(6)、(7)不满足,反演误差较大,本文取0.1倍点距;z₁、z₂的大小需要根据磁异常的信噪比决定,当噪声含量较小时,z₁、z₂可较小。另外,当异常较为复杂时,|z₂-z₁|≤5Δx且z₁和z₂两者取值均不易过大,以避免延拓过大导致不同场源异常相互影响而使反演结果误差增大。需要指出的是,由于反演结果仅在场源位置(x₀,y₀)有效,而远离场源位置的反演结果完全无参考意义,因此在反演图中可仅保留归一化磁源强度垂向差分极大值附近的结果。

2 模型试验

2.1 单一球体

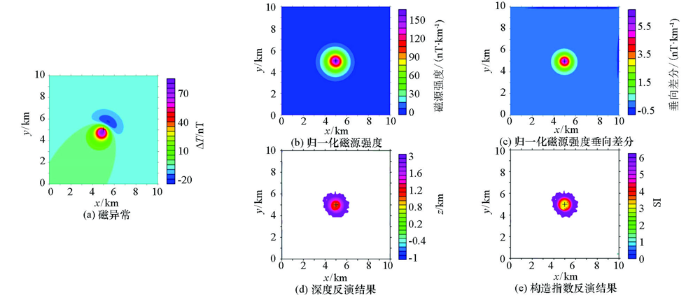
为了验证本文算法的正确性,设计了一个单一球体模型,模型参数为:半径为0.5 km,埋深为1 km,磁化倾角和磁化偏角均为60°,磁化强度为1 A/m。图1a为单一球体模型的磁异常,图1b与1c是归一化磁源强度及其垂向差分结果,可以看出,归一化磁源强度(图1b)极大值与球体质心相吻合,等值线成同心圆分布,异常特征完全不受磁化方向影响,而归一化磁源强度垂向差分(图1c)相对于归一化磁源强度,异常更加汇聚。图1d和1e是本文算法获得的磁源深度及构造指数,可以看出,深度及构造指数反演图均在球体质心位置存在极小值,极小值分别为1.02 km及3.1,均与理论值1 km和3非常接近,这反映了本文算法的正确性。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 单一球体磁异常反演结果(z₁=0 km, z₂=0.2 km)

Fig.1 Inversion results of magnetic anomaly produced by a single sphere model (z₁=0 km, z₂=0.2 km)

2.2 组合模型

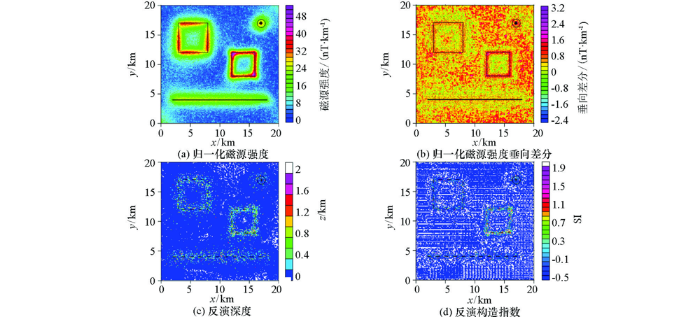
为了验证本文方法对复杂情况的处理能力,设计了一个球体、长方体、薄板、岩脉构成的组合模型,各个模型体参数见表1。图2是组合模型产生的磁异常,可以看出,归一化磁源强度(图3a)能够利用极大值很好地反映出球体质心、棱柱体及薄板边界和岩脉位置;归一化磁源强度垂向差分(图3b)对各模型体刻画的更加精细,异常分辨率获得了明显的提高。图3c、d是本文方法反演得到的场源埋深及构造指数。在球体①质心的反演深度为1.52 km,构造指数反演值为3.0;棱柱体②边界位置上的深度反演解在0.5~0.7 km之间,平均值为0.61 km,构造指数反演解集中在0.2~0.5之间,平均值为0.34;薄板体③边界上的深度反演值在0.47~0.65 km之间,平均值为0.51 km,构造指数在0.55~1之间,平均值为0.77;岩脉④的反演深度集中在1.0~1.15 km,平均值为1.08 km,构造指数在1.05~1.25之间,平均值为1.16。从反演结果可以看出,由于异常叠加影响,反演结果均与理论值存在偏差,但较接近于理论值,且深度反演的平均相对误差仅为8.3%,反演结果仍较可靠。

表1 模型体参数

Table 1 The parameters of the multisource model

模型体编号	模型体类型	边长或半径/ km	上顶或质心埋深/km	下底/ km	磁化方向 (倾角,偏角)	磁化强度/ (A·m^-1)
①	球体(N=3)	0.5	1.5		(45°, 45°)	1
②	棱柱体(N≈0)	5×5	0.5	10	(60°, 45°)	0.1
③	薄板(N≈1)	4×4	0.5	0.6	(0°, 45°)	1
④	岩脉(N=1)	16×0.2	1	100	(30°, 45°)	1

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 组合模型正演磁异常

Fig.2 Forward magnetic anomaly of multi-source model

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 组合模型磁异常的反演结果(延拓点距z₁=0 km,z₂=-0.2 km)

Fig.3 Inversion results of the noise-free synthetic magnetic anomaly (z₁=0 km,z₂=-0.2 km)

为了了解噪声干扰对本文算法的影响情况,对叠加异常(图2)添加了1%的随机噪声,见图4。图5、6和7分别是选取了不同延拓高度的归一化磁源强度及其垂向差分,和深度及构造指数反演结果。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 含1%随机噪声的组合模型磁异常

Fig.4 Synthetic magnetic anomaly added by 1% random noise

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 含噪组合模型磁异常的反演结果(z₁=0 km, z₂=-0.2 km)

Fig.5 Inversion results of noisy magnetic anomaly (z₁=0 km, z₂=-0.2 km)

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 含噪组合模型磁异常的反演结果(z₁=-0.3 km, z₂=-0.5 km)

Fig.6 Inversion results of noisy magnetic anomaly (z₁=-0.3 km, z₂=-0.5 km)

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 含噪组合模型磁异常的反演结果(z₁=-0.5 km, z₂=-0.7 km)

Fig.7 Inversion results of noisy magnetic anomaly (z₁=-0.5 km, z₂=-0.7 km)

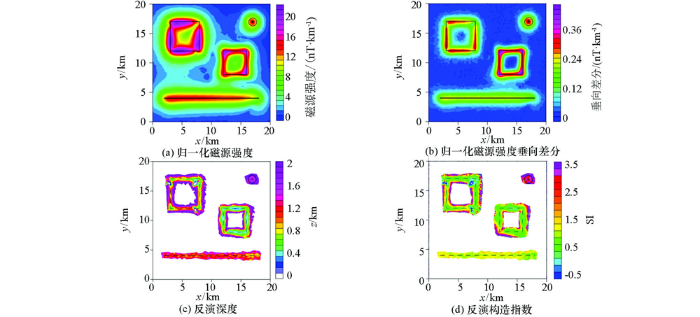
从图5可以看出,未延拓情况下的归一化磁源强度(图5a)虽然存在明显的异常波动,但仍可以清晰地展示出所有模型体的水平位置;垂向差分(图5b)受噪声干扰影响明显,仅能识别出薄板的边界位置,对其他模型反映极为模糊;反演得到的深度(图5c)和构造指数(图5d)也仅在薄板边界上有异常展示,但反演结果波动大,与真值也存在较大偏差。

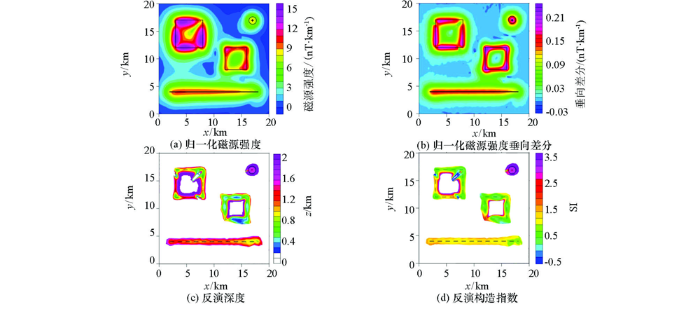
从图6中可以看出,向上延拓3倍点距的归一化磁源强度(图6a)异常较为圆滑,垂向差分(图6b)的稳定性获得较大程度上的提升,能够较好地展示所有模型体的水平位置。图6c和6d是场源深度与构造指数反演结果,表2也给出了无噪声和含噪声不同延拓高度时的反演结果。在该延拓情况下,球体质心埋深反演结果为1.46 km,构造指数为2.88;棱柱体深度反演解在0.4~1.1 km之间,均值为0.74 km,构造指数反演解在0~1.2之间,均值为0.63;薄板的深度反演值在0.4~0.8 km之间,均值为0.51 km,构造指数反演值在0.4~1.5之间,均值为0.76;岩脉深度反演解在0.8~1.4 km之间,均值为1.09 km,构造指数反演值在0.7~1.6之间,均值为1.18。对比无噪声时的反演结果可知,所有模型体的深度反演精度都有所降低,尤其棱柱体深度的相对误差高达48%,不过其他模型体的深度反演误差均小于10%,且深度反演的平均相对误差为 15.4%,因此,认为反演结果仍具有一定的可靠性。

表2 无噪及含噪组合磁异常不同高度上的反演结果

Table 2 Inversion results of noise-free and noise-added synthetic magnetic anomaly at different altitudes

反演结果			球体				棱柱体				薄板				岩脉
反演结果			z₀(1.5)		N(3)		z₀(0.5)		N(0)		z₀(0.5)		N(1)		z₀(1.0)		N(1)
无噪声	z₁=0, z₂=-0.2	1.52		3.00		0.61		0.34		0.51		0.77		1.08		1.16
含噪声	z₁=-0.3, z₂=-0.5	1.46		2.88		0.74		0.63		0.51		0.76		1.09		1.18
含噪声	z₁=-0.5, z₂=-0.7	1.54		3.05		0.94		0.80		0.45		0.61		1.09		1.18

注:深度单位为km。

新窗口打开| 下载CSV

从图7可以看出,向上延拓5倍点距的归一化磁源强度(图7a)及其垂向差分(图7b)异常更加圆滑。图7c和7d是场源深度与构造指数反演结果,球体质心埋深反演结果为1.54 km,构造指数为 3.05;棱柱体深度反演解在0.5~1.4 km之间,均值为0.94 km,构造指数反演解在0.3~1.5之间,均值为0.80;薄板的深度反演值在0.3~0.7 km之间,均值为0.45 km,构造指数反演值在0.3~1之间,均值为0.61;岩脉深度反演解在0.8~1.3 km之间,均值为1.09 km,构造指数反演值在0.5~1.5之间,均值为1.18。对比z₁=-0.3 km,z₂=-0.5 km时的反演结果可知,几乎所有的模型体深度反演精度进一步下降,尤其棱柱体深度的相对误差由48%升至88%,深度反演的平均相对误差为27.4%。由此可见,延拓高度较大时,虽然归一化磁源强度及其垂向差分异常更加光滑,但是反演精度却有所下降,主要在于延拓高度较大时,不同场源的异常相互影响更严重。

3 实例应用

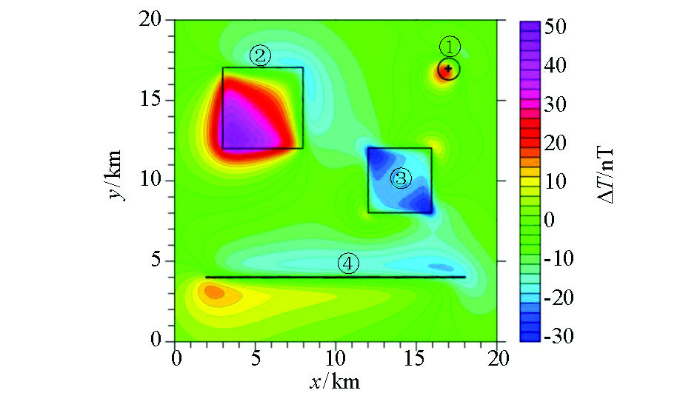
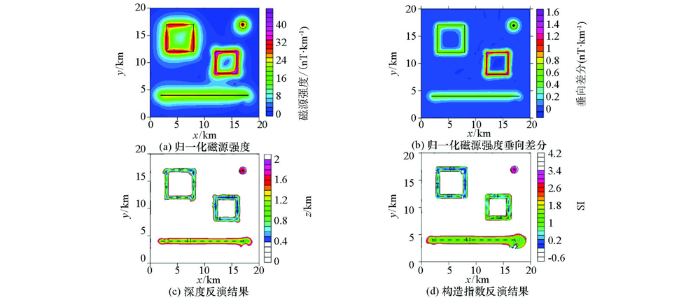
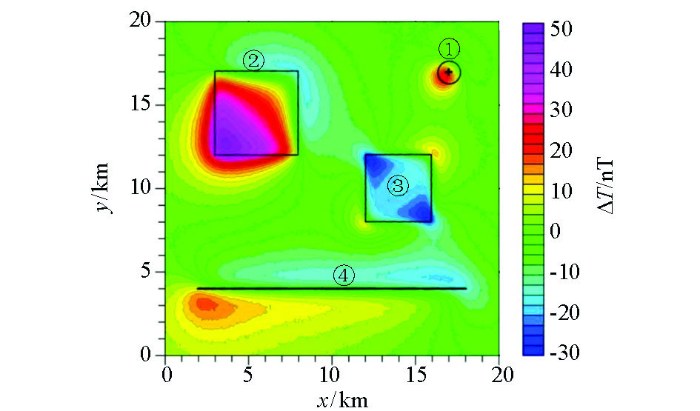
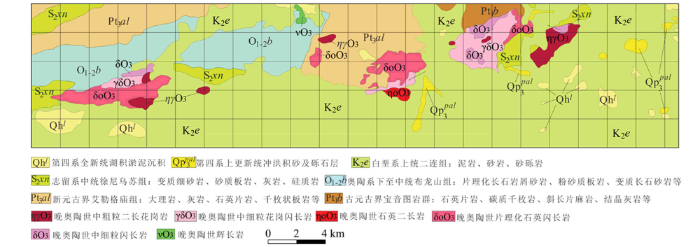
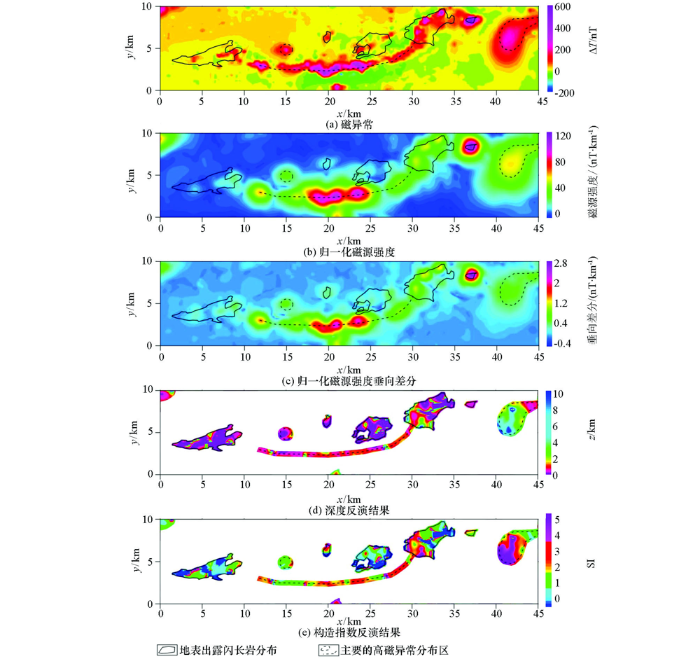
为了验证本文方法的实用性,选取了内蒙古M地区的地面磁异常进行实验。图8是研究区的地质图,可以看出,该地区地表分布的是沉积岩和火山岩,具有一定磁性的晚奥陶世闪长岩主要分布在中西部(东2~10 km,北3~6 km)、中部(东23~28 km,北3~7 km)及中北部(东29~35 km,北5~9 km)3块,其他类型岩石基本无磁性。图9a是研究区地面磁异常,测网密度为250 m(东)×50 m(北),图中可以看出,测区中部存在一条近EW走向转EN走向的条带状磁异常,在测区东部还存在一个明显的高磁异常圈闭区,地表出露的闪长岩上方基本都是以高磁异常显示。图9b是z₁=-0.5 km时的归一化磁源强度,可以看出,归一化磁源强度异常形态更加简洁,高异常分布区与磁异常中的高异常区基本吻合,其主要原因是该地区处于高纬度地区,高磁异常基本与磁性体位置相对应。图9c是z₁=-0.5 km时的归一化磁源强度垂向差分结果,可以看出,该图与归一化磁源强度基本一致,不过异常更加收敛,另外东侧的高异常分布区较模糊,这可能反映了该区磁源埋深较大。图9d和9e是利用本文算法得到的磁源深度z₀及构造指数N分布图,可以看出,地表出露的闪长岩分布区,反演深度基本都是0 km,构造指数多分布在1附近,即可当作岩脉看待;中部条带状磁异常上的深度反演结果基本都在0~1 km之间,即隐伏的高磁性体(推测为闪长岩)埋深相对较浅,构造指数反演结果则由西往东有逐步增加的趋势,基本从1变化到3,这可能是西侧磁性体宽度小而东侧偏大,或东侧磁源从浅往深规模逐渐扩大所致;东部高磁异常圈闭区的深度反演结果表明该磁性体从西南往东北埋深逐渐减小,而构造指数从西南往东北同样逐渐减小,这可能反映了磁性体形态上从穹窿状往脉状的一种转变。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 内蒙古M区地质

Fig.8 Geological map of M area of Inner Mongolia

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 内蒙古M地区磁数据处理(z₁=-0.5 km,z₂=-0.75 km)

Fig.9 Inversion results of magnetic data over M area (z₁=-0.5 km,z₂=-0.75 km)

4 结论

归一化磁源强度是三维磁数据解释常用的方法,主要在于该方法不(少)受磁化方向影响。本文在归一化磁源强度基础上,进行了垂向差分计算,并根据不同高度上差分关系,提出了一种磁源参数快速反演方法。模型分析表明了归一化磁源强度垂向差分提高了原方法的分辨率,能更清晰地展示异常间关系;基于归一化磁源强度垂向差分的反演方法能够有效地反演出磁源的深度与构造指数。在内蒙古M区实例应用中,归一化磁源强度垂向差分识别出了一条近东西走向的高磁异常带和一个范围较大的高磁异常圈闭区,反演算法计算结果表明了东西走向的高磁异常带对应的磁源埋深较浅,形状偏向于岩脉,而高磁异常圈闭区对应的磁源埋深较大。本文提出的磁异常快速反演方法能够很好地估计场源位置信息与几何形状信息,方法原理简单,易于实现,为三维斜磁化磁异常解释提供了新的研究思路。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Peters L

The direct approach to magnetic interpretation and its practical application

[J]. Geophysics, 1949, 14(3):290-320.

DOI:10.1190/1.1437537 URL [本文引用: 1]

[2]

Thompson D

EUDPH: A new technique for making computer assisted depth estimates from magnetic data

[J]. Geophysics, 1982, 47(1):31-37.

DOI:10.1190/1.1441278 URL [本文引用: 1]

[3]

Reid A

, Allsop J

, Granser

, et al.

Magnetic interpretation in three dimensions using Euler deconvolution

[J]. Geophysics, 1990, 55(1):80-91.

DOI:10.1190/1.1442774 URL [本文引用: 1]

[4]

Zhang C

, Mushayandebvu M

, Reid A

, et al.

Euler deconvolution of gravity tensor gradient data

[J]. Geophysics, 2000, 65(2):512-520.

DOI:10.1190/1.1444745 URL [本文引用: 1]

[5]

Huang

, Gubbins

, Clark R

, et al.

Combined study of Euler’s homogeneity equation for gravity and magnetic field

[C]// Extended Abstracts of 57th EAGE Conference, Glasgow, UK, 1995: 144.

[本文引用: 1]

[6]

Salem

, Ravat

A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data

[J]. Geophysics, 2003, 68(6):1952-1961.

DOI:10.1190/1.1635049 URL [本文引用: 1]

[7]

Salem

, Williams

, Fairhead

, et al.

Interpretation of magnetic data using tilt-angle derivatives

[J]. Geophysics, 2008, 71(1):1-10.

[本文引用: 1]

[8]

马国庆, 杜晓娟, 李丽丽.

解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较

[J]. 地球物理学报, 2012, 55(7):2450-2461.

[本文引用: 1]

Ma G

, Du X

, Li L

Comparison of the tensor local wavenumber method with the conventional local wavenumber method for interpretation of total tensor data of potential fields

[J]. Chinese Journal of Geophysics, 2012, 55(7):2450-2461.

[本文引用: 1]

[9]

Atchuta R

, Ram-Babu H

, Sanker-narayan P

Interpretation of magnetic anomalies due to dikes: The complex gradient method

[J]. Geophysics, 1981, 46(11):1572-1578.

DOI:10.1190/1.1441164 URL [本文引用: 1]

[10]

Macleod I

, Jones

, Dai T

3-D analytic signal in the interpretation of total magnetic field data at low magnetic latitudes

[J]. Exploration Geophysics, 1993, 24:679-688.

DOI:10.1071/EG993679 URL [本文引用: 1]

[11]

Salem

, Ravat

, Mushayandebvu M

, et al.

Linearized least-squares method for interpretation of potential-field data from sources of simple geometry

[J]. Geophysics, 2004, 69(3):783-788.

DOI:10.1190/1.1759464 URL [本文引用: 1]

[12]

Salem

Interpretation of magnetic data using analytic signal derivatives

[J]. Geophysical Prospecting, 2005, 53:75-82.

DOI:10.1111/gpr.2005.53.issue-1 URL [本文引用: 1]

[13]

Ma G

, Du X

An improved analytic signal technique for the depth and structural index from 2D magnetic anomaly data

[J]. Pure and Applied Geophysics, 2012, 169:2193-2200.

DOI:10.1007/s00024-012-0484-6 URL [本文引用: 1]

[14]

Cooper G R

The automatic determination of the location and depth of contacts and dykes from aeromagnetic data

[J]. Pure and Applied Geophysics, 2014, 171:2417-2423.

DOI:10.1007/s00024-014-0789-8 URL [本文引用: 1]

[15]

Cooper G R

Using the analytic signal amplitude to determine the location and depth of thin dikes from magnetic data

[J]. Geophysics, 2015, 80(1):J1-J6.

DOI:10.1190/geo2014-0061.1 URL [本文引用: 1]

[16]

Cooper G R

, Whitehead R

Determining the distance to magnetic source

[J]. Geophysics, 2016, 81(2):J25-J34.

[本文引用: 1]

[17]

Cooper G R

Determining the depth and location of potential field sources without specifying the structural index

[J]. Arabian Journal of Geoscience, 2017, 10(438):1-7.

DOI:10.1007/s12517-016-2714-1 URL [本文引用: 1]

[18]

Wang Y

, Luo

, Zhang

Interpretation of 2D magnetic sources based on the reciprocal of the analytic signal amplitude

[J]. Exploration Geophysics, 2019, 50(6):645-652.

DOI:10.1080/08123985.2019.1659101 URL [本文引用: 1]

[19]

Salem

, Williams S

, Fairhead J

, et al.

Tilt-depth method: A simple depth estimation method using fi rst-order magnetic derivatives

[J]. The Leading Edge, 2007, 26(12):1502-1505.

DOI:10.1190/1.2821934 URL [本文引用: 1]

[20]

Fairhead J

, Salem

, Cascone

, et al.

New development of the magnetic tilt-depth method to improve structural mapping of sedimentary basins

[J]. Geophysical Prospecting, 2011, 59:1072-1086.

DOI:10.1111/gpr.2011.59.issue-6 URL [本文引用: 1]

[21]

张恒磊, Marangoni Y

, 左仁广, 等.

改进的各向异性标准化方差探测斜磁化磁异常源边界

[J]. 地球物理学报, 2014, 57(8):2724-2731.

[本文引用: 1]

Zhang H

, Marangoni Y

, Zuo R

, et al.

The improved anisotropy normalized variance for detecting non-vertical magnetization anomalies

[J]. Chinese Journal of Geophysics, 2014, 57(8):2724-2731.

[本文引用: 1]

[22]

Wang Y

, Zhang

, et al.

Improved tilt-depth method for fast estimation of top and bottom depths of magnetic bodies

[J]. Applied Geophysics, 2016, 13(2):249-256.

DOI:10.1007/s11770-016-0551-3 URL [本文引用: 1]

[23]

Cooper G R

Applying the tilt-depth and contact-depth methods to the anomalies of thin dykes

[J]. Geophysical Prospecting, 2017, 65:316-323.

DOI:10.1111/gpr.2017.65.issue-1 URL [本文引用: 1]

[24]

曹伟平, 王彦国, 杨博

等.

Tilt-depth 方法适用性研究及其应用

[J]. 世界地质, 2017, 36(2):560-569.

[本文引用: 1]

Cao W

, Wang Y

, Yang

, et al.

Applicability of tilt-depth method and its application

[J]. World Geology, 2017, 36(2):560-569.

[本文引用: 1]

[25]

Wilson H

Analysis of the magnetic gradient tensor

[J]. Canada Technical Memorandum, 1985, 8:5-13.

[本文引用: 2]

[26]

Beiki

, Clark D

, Austin J

, et al.

Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data

[J]. Geophysics, 2012, 77(6):J23-J37.

DOI:10.1190/geo2011-0437.1 URL [本文引用: 2]

[27]

Pikington

, Beiki

Mitigating remanent magnetization effects in magnetic data using the normalized source strength

[J]. Geophysics, 2013, 78(3):J25-J32.

DOI:10.1190/geo2012-0225.1 URL [本文引用: 1]

[28]

Guo L

, Meng X

, Zhang G

Three-dimensional imaging for total amplitude magnetic anomaly and normalized source strength in the presence of strong remanent magnetization

[J]. Journal of Applied Geophysics, 2014, (111):121-128.

[本文引用: 1]

[29]

饶椿锋, 于鹏, 胡书凡, 等.

基于加权模型参数的归一化磁源强度三维反演

[J]. 石油物探, 2017, 56(4):599-606.

[本文引用: 1]

Rao C

, Yu

, Hu S

, et al.

The 3D inversion of the normalized source strength data based on weighted model parameters

[J]. Geophysical Prospecting for Petroleum, 2017, 56(4):599-606.

[本文引用: 1]

[30]

Blakely R

. Potential theory in gravity and magnetic applications [M]. London: Cambridge University Press, 1995.

[本文引用: 1]

[31]

Pedersen L

, Rasmussen T

The gradient tensor of potential field anomalies: Some implications on data collection and data processing of maps

[J]. Geophysics, 1990, 55(12):1558-1566.

DOI:10.1190/1.1442807 URL [本文引用: 1]

The direct approach to magnetic interpretation and its practical application

1949

... 磁异常快速反演一直是磁法数据处理与解释的研究重点与热点,该类方法能够在无先验信息约束下快速获取场源的位置与几何参数.目前较为常用的快速反演方法有欧拉反褶积法、解析信号法、tilt-depth法等.欧拉反褶积是Peters^[1]提出的,Thompson^[2]推导了二维欧拉反褶积,Reid 等^[3]将其推广至三维.张量欧拉反褶积^[4]扩展了欧拉方程个数,提高了反演解收敛性;Huang 等^[5]证明了位场解析信号同样满足欧拉齐次方程;AN-EUL 法^[6]能够快速估算场源深度与构造指数; Tilt-Euler 法^[7]无需已知场源构造指数,避免了因构造指数选取不当导致反演解发散的问题;张量局部波数的欧拉反褶积法^[8]进一步扩展了方程组个数,获得了良好的应用效果.不过欧拉反褶积及其改进方法的反演解中存在大量的虚假解,需要建立有效的筛选机制,另外背景场、噪声干扰及窗口大小选择也会对反演结果产生一定影响.二维磁解析信号振幅不受磁化方向影响^[9],Macleod ^[10]推导出了二维磁解析信号振幅的通用表达式;Salem 等^[11]在解析信号及其水平总梯度基础上采用线性最小二乘法计算磁源深度及构造指数;Salem 等^[12]又根据解析信号及磁异常垂向导数解析信号关系进行磁源参数估计;Ma 和Du^[13]在解析信号振幅的解析信号与解析信号比值基础上提出了改进解析信号来实现单一场源深度及构造指数的估算;Cooper^[14,15]同样采用不同阶次解析信号来估计岩脉及台阶的深度;Cooper 和Whitehead^[16]利用不同阶次解析信号比值进行场源深度估算,不过改进方法不需要已知构造指数;Cooper^[17]又采用了解析信号对数实现磁源深度估计工作.Wang等^[18]采用解析信号及其倒数进行磁源参数反演计算,对深部场源反演效果较好.但三维解析信号在一定程度上受磁化角度影响,在三维磁异常反演中使用较小.Tilt-depth 法可用于快速估算场源上顶深度,该方法是由Salem 等^[19]在Tilt 梯度及磁场通用梯度公式进行理论推导而来; Fairhead 等^[20]提出了基于化极与化赤相结合的tilt-depth 法,还可以实现场源磁化率估计;张恒磊等^[21]提出了基于二阶导数的磁源边界与顶部深度快速反演方法,有效地消除了区域场对反演结果的影响; Wang 等^[22]提出了改进tilt-depth 法来估计磁源的上顶与下底深度,并采用多特征点联合计算来提高反演解的可靠性;Cooper ^[23]在Hilbert 变换基础上推导出了岩脉模型的垂直磁化磁位的tilt-depth 公式,提高了方法实用性及稳定性;曹伟平等^[24]对tilt-depth 法进行了深入研究,指出了该方法并不适用于埋深大、水平尺度小的磁源深度反演计算.由于tilt-depth 法及改进算法均需要在化极或化赤基础上完成计算,因此并不能直接用于斜磁化磁源深度的估算. ...

EUDPH: A new technique for making computer assisted depth estimates from magnetic data

1982

Magnetic interpretation in three dimensions using Euler deconvolution

1990

Euler deconvolution of gravity tensor gradient data

2000

Combined study of Euler’s homogeneity equation for gravity and magnetic field

1995

A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data

2003

Interpretation of magnetic data using tilt-angle derivatives

2008

解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较

2012

解释位场全张量数据的张量局部波数法及其与常规局部波数法的比较

2012

Interpretation of magnetic anomalies due to dikes: The complex gradient method

1981

3-D analytic signal in the interpretation of total magnetic field data at low magnetic latitudes

1993

Linearized least-squares method for interpretation of potential-field data from sources of simple geometry

2004

Interpretation of magnetic data using analytic signal derivatives

2005

An improved analytic signal technique for the depth and structural index from 2D magnetic anomaly data

2012

The automatic determination of the location and depth of contacts and dykes from aeromagnetic data

2014

Using the analytic signal amplitude to determine the location and depth of thin dikes from magnetic data

2015

Determining the distance to magnetic source

2016

Determining the depth and location of potential field sources without specifying the structural index

2017

Interpretation of 2D magnetic sources based on the reciprocal of the analytic signal amplitude

2019

Tilt-depth method: A simple depth estimation method using fi rst-order magnetic derivatives

2007

New development of the magnetic tilt-depth method to improve structural mapping of sedimentary basins

2011

改进的各向异性标准化方差探测斜磁化磁异常源边界

2014

改进的各向异性标准化方差探测斜磁化磁异常源边界

2014

Improved tilt-depth method for fast estimation of top and bottom depths of magnetic bodies

2016

Applying the tilt-depth and contact-depth methods to the anomalies of thin dykes

2017

Tilt-depth 方法适用性研究及其应用

2017

Tilt-depth 方法适用性研究及其应用

2017

Analysis of the magnetic gradient tensor

1985

... 归一化磁源强度是在磁梯度张量特征值基础上提出的,该方法不(少)受磁化方向影响,是三维磁异常解释的常用工具.Wilson^[25]首先给出了磁偶极子下归一化磁源强度的表达式,Beiki等^[26]给出了归一化磁源强度的通用表达形式,建立了归一化磁源强度与场源位置、构造指数的关系,同时结合欧拉反褶积实现了三维磁源的位置及构造指数反演;Pikington 和Beiki^[27]在归一化磁源强度基础上实现了剩磁情况下的磁源空间位置及磁化率反演;Guo等^[28] 将归一化磁源强度与相关成像结合来反映地下磁性体的三维空间展布状态;饶椿锋等^[29]将归一化磁源强度与正则化共轭梯度法结合来反演磁源的磁化率.本文在归一化磁源强度垂向差分基础上,提出了一种场源快速反演方法,并进行了模型分析与实例应用. ...

... 式中:l₁、l₂和l₃为Γ的特征向量;λ₁、λ₂、λ₃为对应的特征值.Wilson^[25]给出磁偶极子的归一化磁源强度μ的定义,并推导出梯度张量特征值表达式: ...

Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data

2012

... Beiki等^[26]给出了归一化磁源强度的统一表达式: ...

Mitigating remanent magnetization effects in magnetic data using the normalized source strength

2013

Three-dimensional imaging for total amplitude magnetic anomaly and normalized source strength in the presence of strong remanent magnetization

2014

基于加权模型参数的归一化磁源强度三维反演

2017

基于加权模型参数的归一化磁源强度三维反演

2017

1995

... 对于体积为V,磁化强度为M的磁性体,其磁位U的表达式^[30]为: ...

The gradient tensor of potential field anomalies: Some implications on data collection and data processing of maps

1990

... 磁梯度张量^[31]可以表示为: ...

〈

〉