iTilt-Euler法在重力数据处理及断裂解释中的应用

doi:10.11720/wtyht.2021.0284

iTilt-Euler法在重力数据处理及断裂解释中的应用

陈青^,¹^,², 孙帅¹, 丁成艺¹, 黄小宇¹, 陈浩³, 申鹏¹, 罗港¹, 魏耀聪¹

1.重庆科技学院石油与天然气工程学院,重庆 401331

2.复杂油气田勘探开发重庆市重点实验室,重庆 401331

3.重庆市二零八地质环境工程勘查设计院有限公司,重庆 400700

Application of iTilt-Euler deconvolution in gravity data processing and fault system interpretation

CHEN Qing^,¹^,², SUN Shuai¹, DING Cheng-Yi¹, HUANG Xiao-Yu¹, CHEN Hao³, SHEN Peng¹, LUO Gang¹, WEI Yao-Cong¹

1. Department of Earth Science, School of Petroleum and Natural Gas Engineering, Chongqing University of Science and Technology, Chongqing 401331, China

2. Chongqing Key Laboratory of Complex Oil and Gas Exploration and Development, Chongqing 401331, China

3. Chongqing 208 Geoenvironmental Engineering Survey and Design Institute Co., Ltd., Chongqing 400700, China

责任编辑: 王萌

收稿日期: 2021-05-18 修回日期: 2021-06-20

基金资助:

国家自然科学基金项目.  41702210
重庆市基础科学与前沿技术研究专项.  cstc2017jcyjAX0370
重庆市教委科学技术研究项目.  KJQN201901535
重庆科技学院博士教授科研启动基金项目.  CK2016B12

Received: 2021-05-18 Revised: 2021-06-20

作者简介 About authors

陈青(1984-),女,博士,2015年毕业于西北大学,主要研究方向为构造地球物理。Email: chenqing0144@126.com

摘要

为改善欧拉反演结果的收敛性,本文采用不依赖于构造指数的改进Tilt-Euler(iTilt-Euler)进行计算,并利用水平总梯度倾斜角峰值(TAHG)约束法约束反演数据,优化计算结果。模型试算结果表明,采用TAHG法约束的iTilt-Euler反演结果的收敛性得到了有效提高,且为深源地质体的位置和深度提供了更多信息。在肯尼亚ANZA盆地某区块重力数据处理中的应用表明,TAHG法约束下的iTilt-Euler反演解连续性较好,主要呈NW向,其次是NE向,且NW向展布的解延伸长、深度大,反映为控制区内构造单元边界的基底断裂,被NE向展布的盖层断裂所切割。此外,研究区东南部发育一条NNE向的深断裂,切割了NW向及NE向断裂,推测其可能控制了区域构造单元的东南边界。应用结果表明,iTilt-Euler法和TAHG法可为断裂解释提供可靠的研究手段,具有较好的实用性。

关键词： 欧拉反褶积 ; 重力异常 ; 倾斜角 ; 断裂系统

Abstract

In order to improve the convergence and stability of Euler inverted results, the iTilt-Euler method, which do not depend on the structure index, is used for the calculation. Furthermore, the data points are constrained by the peak values of tilt angle of the total horizontal derivative (TAHG) to optimize the solutions. The method has been demonstrated with synthetic and real data. For synthetic data, the convergence of iTilt-Euler inversion results constrained by the TAHG method is improved effectively to detect the fault structures with deeper depth. Application to gravity data for the ANZA basin in Kenya shows that the iTilt-Euler inversion results constrained by peak values of TAHG have good continuity. The results distribute generally along NW direction, followed by NE direction, and these characteristics are consistent with the identifying features of fault in the second-order vertical derivative and total horizontal derivative anomaly maps. Furthermore, the inversion depth results show that the solutions along NW direction are extend to large scale and with higher values, which is reflected as a basement fault that controls the boundary of the main tectonic units in the study area and usually cut by the superficial faults with NE extension. It is worth noting that a large deep fault with NNE extension is developed in the southeast of the study area, which cuts the north-west direction and the north-east direction fault. It is speculated that it may control the southeast boundary of the regional tectonic unit. We can conclude that the iTilt-Euler deconvolution combined with the peak constraint method can provide a reliable method for fault system interpretation, and has good practicability.

Keywords： Euler deconvolution ; gravity anomaly ; Tilt angle ; fault system

PDF (4071KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

陈青, 孙帅, 丁成艺, 黄小宇, 陈浩, 申鹏, 罗港, 魏耀聪. iTilt-Euler法在重力数据处理及断裂解释中的应用. 物探与化探[J], 2021, 45(6): 1578-1587 doi:10.11720/wtyht.2021.0284

CHEN Qing, SUN Shuai, DING Cheng-Yi, HUANG Xiao-Yu, CHEN Hao, SHEN Peng, LUO Gang, WEI Yao-Cong. Application of iTilt-Euler deconvolution in gravity data processing and fault system interpretation. Geophysical and Geochemical Exploration[J], 2021, 45(6): 1578-1587 doi:10.11720/wtyht.2021.0284

0 引言

重力异常场包含了地表及地下诸多密度不均匀体场源产生的综合信息,直观地反映了地下地质体的分布位置、深部构造以及断裂展布等信息。重力资料解释中最重要的目的是定性和定量地推断地下客观存在的异常体的位置、深度、几何形态及物性参数的过程。然而,受各种密度不均匀体叠加效应的影响,重力异常平面等值线特征往往不能较好地标识深、浅部地质体的信息,无疑增加了重力资料解释的难度。因此,迫切需要一种能够将重力场异常进行自动化或半自动化处理和解释的方法和技术,以提取更多的有效信息。欧拉反褶积作为一种能自动、快速估算场源位置和深度的方法便应运而生。该方法以欧拉齐次方程为基础,运用位场异常、空间导数,根据场源形状选择构造指数,通过欧拉齐次方程的求解,自动或半自动的圈定地质体的边界及深度^[1,2,3]。该方法的优点是无需已知场源物性的先验信息,只需要事先确定与场源性质有关的构造指数,便可快速、有效地推算出地质体的具体位置,尤其适用于大面积位场数据的分析和解释^[3]。理论上,欧拉反演结果对应于重磁异常平面上的特征区域,如线性梯级带、规则性扭曲的等值线或水平错动的异常轴等,而断裂往往出现在这些区域,因此,欧拉反褶积法在圈定场源体边界和识别断裂中具有重要意义。

尽管欧拉反褶积方法在位场数据自动反演中得到了广泛应用,但在实际应用中,受地质体的复杂性和场源体之间的叠加影响,该方法存在反演结果发散、虚假解,以及复杂情况下构造指数的确定等问题,制约了该方法实际应用。为了改善欧拉解的发散性,提高反演精度,国内外众多学者从不同数据源、构造指数选取、消除虚假解等方面做了大量的工作。

在利用不同数据源改善反演结果的发散性方面,Hsu^[4]提出了利用重力高阶导数进行欧拉反演,大大减小了反演位置和深度解的扩散;Salem等^[5]将欧拉反褶积方法与解析信号法相结合,利用解析信号幅度的极大值直接估算出场源的深度及构造指数;Salem等^[6]将欧拉反褶积方法与Tilt 梯度相结合,该方法无需构造指数就能推断出场源边界和深度分布,从而避免了因构造指数选取导致欧拉反演解的发散和不稳定;范美宁等^[7]通过模型计算,证明了用高阶导数或解析信号进行欧拉反演计算,可提高反演结果的收敛性;Ma等^[8]推导出了归一化倾斜角(TDX)和Theta图的欧拉反褶积形式,该形式与Tilt梯度法的欧拉方程形式类似,不受构造指数选取的影响,提高了反演结果的收敛性。

在提高算法精度方面,Neil 等^[9]讨论了如何获得相对稳定的最小二乘解;Fairhead等^[10]提出利用拉普拉斯方程滤波法来消除欧拉方程的发散解;Keating^[11]通过对误差函数的欧拉方程进行加权计算来消除假频信号的干扰;范美宁等^[12]把最小二乘问题转化成了解线性方程的问题,从而减少了计算量,减小了误差传递;Davis和Li^[13]讨论了利用异常数据的振幅信息来降低噪声和发散解对场源深度估算的干扰。周勇等^[14]采用截断奇异值分解法解欧拉齐次方程,将异常源边界及中心欧拉解的截断误差最小的解作为最优解。

在有效剔除虚假解方面,Gerovska和Araúzo-Bravo^[15]通过微分相似变换提取欧拉解奇异点处的虚假解,并利用欧拉解标准差构造评价标准剔除解集中的虚假解;姚长利等^[3]提出水平梯度滤波准则、距离约束评价准则和聚集度约束评价准则等方法,推动了欧拉反褶积实用化研究;Ugalde和Morris^[16]提出采用聚类分析和内核密度估算技术来解决欧拉解中虚假解的问题;Salem等^[17]采用倾斜角水平总梯度峰值来约束反演数据范围,有效提高了反演结果的收敛性;Beiki等^[18]利用截断奇异值分解方法对误差相对较大的欧拉解进行剔除,以提升欧拉反褶积对磁源异常的确定精度。

构造指数的确定在欧拉反褶积法求解过程中至关重要,需要根据场源形状或有关异常性质的先验知识来选择。在实际应用中,利用经验获取的构造指数进行欧拉反演,往往导致反演结果不准确或解的发散。在构造指数选取方面,Neil 等^[9]提出利用统计方法来推断出构造指数;Salem等^[5]利用解析信号幅度的极大值来自动推算构造指数;Barbosa等^[19]提出利用欧拉方程中位场总场值f与背景场B之间最小线性相关来获取构造指数最佳解;姚长利等^[3]采用变构造指数对数据滑动窗口重复扫描,从而使得场源解更集中;郭志宏^[20]提出将自动估算场源的构造指数的办法与异常位置及范围的自动识别方法相结合,形成了一套智能型的改进欧拉反褶积方法;Salem等^[6]提出利用不依赖于构造指数的Tilt-Euler法快速推断出场源边界和深部,在此基础上自动估算出构造指数的分布;鲁宝亮等^[21]提出通过建立欧拉反褶积的超定方程组,求解出最佳构造指数;曹书锦等^[22]将截断误差与核密度估计进行相关分析,确定最优构造指数。

为减小由经验获取的构造指数计算结果的发散性,本文利用不依赖于构造指数的Tilt-Euler法和改进Tilt-Euler法,进行了正演模型计算和对比分析;同时,采用水平总梯度倾斜角峰值约束反演解,优化计算结果。最后,将其应用于肯尼亚ANZA盆地中部地区重力数据处理中,划分出研究区的断裂构造体系,为ANZA盆地的进一步地球物理工作提供依据。

1 改进Tilt-Euler法基本原理

1.1 倾斜角法

倾斜角(tilt Derivative)是为了识别不同埋深的场源体边界提出的方法,该方法利用总场强f的垂直梯度(VDR)比水平总梯度(THDR)的绝对值的反正切角度^[23],定义为:

(1)

θ = \arctan \frac{VDR}{THDR} = \arctan \frac{(\partial f / \partial z)}{(\partial f / \partial h)},

式(1)中:

(2)

\frac{\partial f}{\partial h} = \sqrt[]{{(\partial f / \partial x)}^{2} + {(\partial f / \partial y)}^{2}},

其中:∂f/∂x、∂f/∂y和∂f/∂z分别为总场强f沿x、y和z方向的一阶导数。根据反正切函数的性质,倾斜角的变化范围为(-π/2,π/2),在场源体内为正值,外围为负值,边界处为零。对于深部场源,在其垂向导数和水平导数都很小的情况下,两者的比值仍然可以很大,因此,倾斜角反演结果受地质体埋深的影响很小^[23,24]。然而,在区域背景场下,位于倾斜角分母上的水平总梯度(THDR)可能趋近于0,导致倾斜角存在“解析奇点”^[25]。因此,刘鹏飞等^[26]对倾斜角进行了改进,其数学定义式为:

(3)

iTilt = \arctan \frac{\partial f / \partial z}{\sqrt[]{{(\partial f / \partial x)}^{2} + {(\partial f / \partial y)}^{2} + {(\partial f / \partial z)}^{2}}},

其中:分母为场强的解析信号振幅A。式(3)中,利用解析信号振幅替换了分母水平总梯度模,提高了计算结果的稳定性^[26]。同时,改进的倾斜角继承了倾斜角对弱异常提取的优势,从而能很好识别出埋深不同的隐伏场源信息。

1.2 Tilt-Euler法及iTilt-Euler法

欧拉反褶积的基本公式表示为^[1]:

(4)

\begin{array}{l} (x - x_{0}) \frac{\partial f}{\partial x} + (y - y_{0}) \frac{\partial f}{\partial y} + (z - z_{0}) \frac{\partial f}{\partial z} \\ = - N (f - B), \end{array}

式中:f为场源位场异常;x、y、z为观测点的坐标;x₀、y₀、z₀为场源坐标;N为构造指数(N=1,2,…),与场源的几何构造有关,是场源异常强度随深度变化的衰减率;B称为区域场或背景场。由此可见,该方法是以欧拉齐次方程为基础,运用位场异常及其空间导数,结合地质体特定的“构造指数”来确定异常场源的位置和深度。然而,由于实际地质构造的场源类型复杂多样,构造指数值选择的正确与否直接影响到了场源深度反演解的准确性和稳定性。

Salem等^[17]根据倾斜角公式推导出了基于倾斜角的欧拉反褶积,即Tilt-Euler。该方法的优势是不依赖于已知场源的构造指数,可方便估算出场源的位置分布,提高了欧拉反褶积方法的实用性。Tilt-Euler方程为^[17]:

(5)

k_{x} x_{0} + k_{y} y_{0} + k_{z} z_{0} = k_{x} x + k_{y} y + k_{z} z,

其中:k_x,k_y,k_z分别是沿x、y、z方向的倾斜角的导数,分别表示为^[17]:

(6)

k_{x} = \frac{\partial Tilt}{\partial x} = \frac{1}{A^{2}} [\frac{\partial f}{\partial h} \frac{\partial^{2} f}{\partial x \partial z} - (\frac{(\frac{\partial f}{\partial z})}{(\frac{\partial f}{\partial h})}) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y \partial x})],

(7)

k_{y} = \frac{\partial Tilt}{\partial y} = \frac{1}{A^{2}} [\frac{\partial f}{\partial h} \frac{\partial^{2} f}{\partial y \partial z} - (\frac{(\frac{\partial f}{\partial z})}{(\frac{\partial f}{\partial h})}) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x \partial y} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y^{2}})]

(8)

k_{z} = \frac{\partial Tilt}{\partial z} = \frac{1}{A^{2}} [\frac{\partial f}{\partial h} \frac{\partial^{2} f}{\partial z^{2}} - (\frac{(\frac{\partial f}{\partial z})}{(\frac{\partial f}{\partial h})}) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x \partial z} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y \partial z})]

其中:A= $\sqrt[]{{(\frac{\partial f}{\partial x})}^{2} + {(\frac{\partial f}{\partial y})}^{2} + {(\frac{\partial f}{\partial z})}^{2}}$ 为场强的解析信号振幅。式(5)与常规欧拉反褶积方程类似,但不包含构造指数。因此,避免了常规欧拉反褶积方法因构造指数选取偏差导致的反演结果发散的问题,为实际位场资料处理解释提供了有效手段。然而,式(6)~(8)中,仍然存在水平总梯度位于分母的情况。因此,在水平总梯度趋于零时,k_x,k_y,k_z的结果中存在解析奇点。针对这一问题,Huang等^[27]基于改进倾斜角(即式(3))推导了其欧拉反褶积形式,记为iTilt-Euler,表达式如下^[27]:

(9)

k_{x}^{'} x_{0} + k_{y}^{'} y_{0} + k_{z}^{'} z_{0} = k_{x}^{'} x + k_{y}^{'} y + k_{z}^{'} z,

式(9)与式(5)形式类似。其中 $k_{x}^{'}$ 、 $k_{y}^{'}$ 、 $k_{z}^{'}$ 分别是改进倾斜角沿x、y、z方向导数,表示为^[27]:

(10)

k_{x}^{'} = \frac{\partial iTilt}{\partial x} = \frac{1}{A'^{2}} [A \frac{\partial^{2} f}{\partial x \partial z} - ((\frac{\partial f}{\partial z}) / A) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y \partial x} + \frac{\partial f}{\partial z} \frac{\partial^{2} f}{\partial z \partial x})]

(11)

k_{y}^{'} = \frac{\partial iTilt}{\partial y} = \frac{1}{A'^{2}} [A \frac{\partial^{2} f}{\partial y \partial z} - ((\frac{\partial f}{\partial z}) / A) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x \partial y} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y^{2}} + \frac{\partial f}{\partial z} \frac{\partial^{2} f}{\partial z \partial y})]

(12)

k_{z}^{'} = \frac{\partial iTilt}{\partial z} = \frac{1}{A'^{2}} [A \frac{\partial^{2} f}{\partial z^{2}} - ((\frac{\partial f}{\partial z}) / A) \cdot (\frac{\partial f}{\partial x} \frac{\partial^{2} f}{\partial x \partial z} + \frac{\partial f}{\partial y} \frac{\partial^{2} f}{\partial y \partial z} + \frac{\partial f}{\partial z} \frac{\partial^{2} f}{\partial z^{2}})]

其中:A'= $\sqrt[]{{(\frac{\partial f}{\partial z})}^{2} + A^{2}}$ 。改进倾斜角的各方向导数的求解过程中,仅有解析信号振幅A位于分母。然而,即使在A趋于0的情况下,其各方向导数公式(10)~(12)中均不存在“解析奇点”,关系如下^[27]:

(13)

\begin{array}{r} \lim_{A \to 0} [(\frac{\partial f}{\partial z}) / A] & = \lim_{A \to 0} [\frac{(\frac{\partial f}{\partial z})}{\sqrt[]{{(\frac{\partial f}{\partial x})}^{2} + {(\frac{\partial f}{\partial y})}^{2} + {(\frac{\partial f}{\partial z})}^{2}}}] \\ = \lim_{A \to 0} [\frac{(\frac{\partial f}{\partial z})}{\sqrt[]{0 + {(\frac{\partial f}{\partial z})}^{2}}}] \\ = \lim_{\frac{\partial f}{\partial z} \to 0} [\frac{(\frac{\partial f}{\partial z})}{|\frac{\partial f}{\partial z}|}] = \pm 1 。 \end{array}

因此,仍然可以计算 $k_{x}^{'}$ , $k_{y}^{'}$ , $k_{z}^{'}$ 的值。iTilt-Euler不仅继承了Tilt-Euler法不依赖于构造指数的优点,还可有效提高反演结果的稳定性。

1.3 水平总梯度倾斜角峰值约束法

为了提高反演结果的收敛性,Salem等^[17]提出利用一定范围内的倾斜角水平总梯度峰值来约束网格点,从而有效减少了发散解。本文提出利用水平总梯度倾斜角TAHG峰值对反演数据点进行约束,其表达式为^[28]:

(14)

TAHG = \arctan (\frac{\partial THDR / \partial z}{\sqrt[]{{(\partial THDR / \partial x)}^{2} + {(\partial THDR / \partial y)}^{2}}}) 。

由于反正切的特点,TAHG变换范围也为(-π/2,π/2)。该方法不仅有效平衡了来自浅源和深源的信息,同时最大值位于场源体边界。因此,本文利用TAHG的最大值范围对欧拉反褶积的数据点进行约束,从而提高反演结果的收敛性。

本文提出利用倾斜角水平总梯度峰值来约束数据点,通过改进倾斜角沿x、y、z方向导数的峰值建立欧拉方程组,求解出场源体位置参数。具体步骤如下:

1) 计算重力异常在x,y和z方向进行一阶、二阶导数,即V_zx、V_zy、V_zz、V_zxx、V_zxy、V_zyy、V_zzx、V_zzy、V_zzz;

2) 利用公式(10)、(11)、(12),求得改进倾斜角沿x、y、z方向导数 $k_{x}^{'}$ 、 $k_{y}^{'}$ 、 $k_{z}^{'}$ ;

3) 利用式(14),求得水平总梯度倾斜角TAHG,并提取其峰值;

4) 以TAHG的峰值作为约束,选取 $k_{x}^{'}$ 、 $k_{y}^{'}$ 和 $k_{z}^{'}$ 的峰值,并将其代入式(9);

5) 设置一定的滑动窗口,在窗口内建立欧拉方程组,求解出场源体的位置参数x₀、y₀和z₀结果,即水平位置和深度;

6) 按一定步长滑动子窗口,重复第5步,直至覆盖全区;

7) 将欧拉反演结果成图并进行解释。

2 模型试算

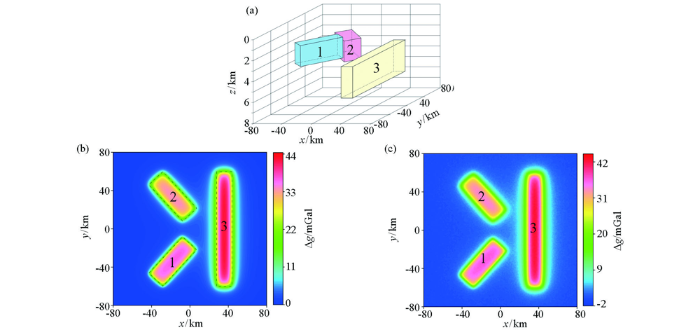
为了验证iTilt-Euler在位场数据处理中的实际应用效果,本文选取3个剩余密度均为0.5×10³ kg/m³,但顶面埋深和厚度不同的立方体进行理论模型正演计算,模型三维立体图如图1a所示,模型参数见表1。图1b为组合模型的理论重力异常,网格间距为0.8 km×0.8 km。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 组合模型重力异常正演(黑色虚线为模型体位置)

a—组合模型三维立体图;b—组合模型重力异常;c—添加2%高斯噪声的组合模型重力异常

Fig.1 Gravity anomaly forward modeling of conbined model (the black dotted lines represent the actual edges of the models)

a—sketch representation of combined model;b—gravity anomaly of combined model;c—random noise with amplitude equal to 2% of maimum data amplitude was added to the gravity anomaly of combined model

表1 组合模型参数

Table1 Combined model parameters

模型体	中心点坐标/km	长度/km	宽度/km	顶面埋深/km	厚度/km	旋转角度/(°)
1	(-18,-34)	52	20	1	2	-45
2	(-18,34)	52	20	2	2	45
3	(36,0)	120	16	3	3	0

新窗口打开| 下载CSV

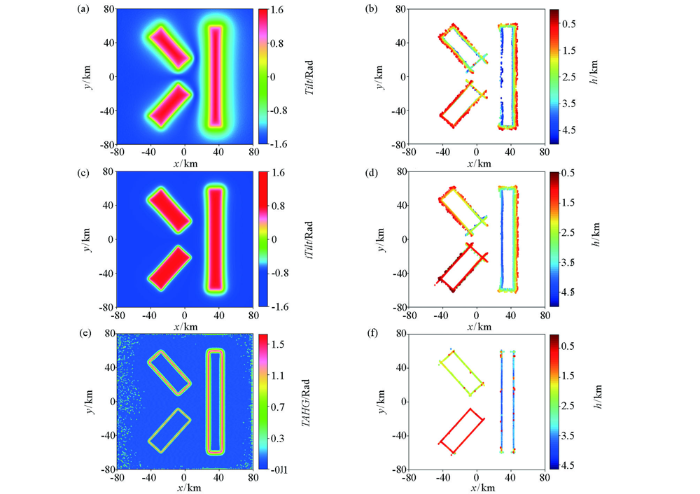
由图1b可以看出,模型1埋深较浅,异常幅值基本能勾勒出场源边缘位置,而对于埋深较深的模型3,因受场源叠加的影响,异常幅值偏向场源边界外侧,且发生扭动。图2a和2c分别是倾斜角和改进倾斜角的计算结果,由零值反映的边界位置来看,两种方法都增强了埋深较深的弱异常信息,但改进倾斜角有效降低了倾斜角的高幅值畸变成分,使得计算结果更为稳定。水平总梯度倾斜角(图2e)不仅有效增强了弱异常信息,并且其最大值反映的地质体边界与实际位置也吻合较好。图2b和2d分别为倾斜角和改进倾斜角在不加峰值约束下的欧拉反演结果,滑动窗口大小选择11×11。可以看出,两种方法的计算结果较相似,但由于改进倾斜角的边界位置相对收敛,其欧拉解的连续性更好,虚假解也较少。然而,从iTilt-Euler反演结果来看,浅源地质体的欧拉解虽然连续性较好,但由于受浅层高频异常的影响,估算深度明显比实际深度小,同时使得深源地质体的欧拉结果出现了大量小于真实值的虚假解。相对而言,水平总梯度倾斜角及其约束之下的iTilt-Euler法反演结果(图2f)较为收敛,场源解集中分布在场源体边界处,较好地反映出了模型体的水平位置和深度。约束下的iTilt-Euler法反演的3个模型体深度结果分别为0.94±0.01 km,2.14±0.02 km和3.27±0.02 km,误差分别为6%、7%和9%,与理论埋深值吻合度较高。因此,利用水平总梯度倾斜角峰值约束反演数据,可以有效减小场源异常相互叠加的影响,使得深源位置也得到较好的反映。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不加噪组合模型欧拉反演结果

a—倾斜角;b—Tilt-Euler法反演结果;c—改进倾斜角;d—iTilt-Euler法反演结果;e—水平总梯度倾斜角;f—水平总梯度倾斜角峰值约束下的iTilt-Euler法反演结果

Fig.2 Results of Euler deconvolution based on the combined model without noise

a—tilt angle;b—estimated results from the Tilt-Euler; c—improved tilt angle; d—estimated results from the iTilt-Euler; e—total horizontal derivative of tilt angle; f—estimated results from the iTilt-Euler under the peak constraint of total horizontal derivative of tilt angle

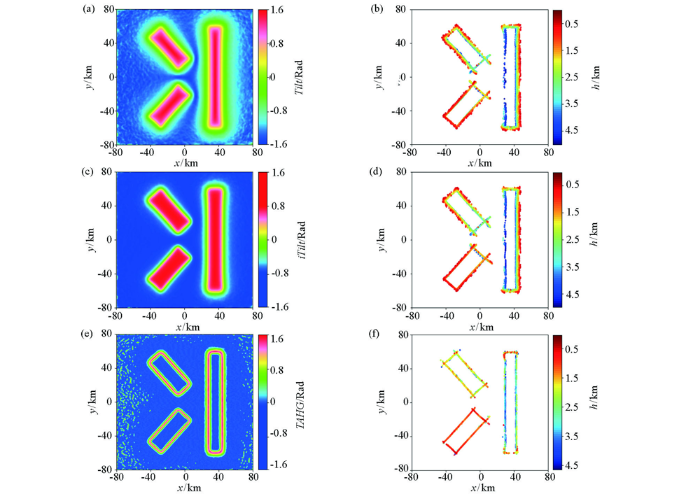
由于实际位场数据包含一定的噪声,为了进一步检验反演结果的稳定性, 对组合模型加入了2%高斯噪声(图1c)进行计算,并与Tilt-Euler法反演结果进行了比较。加噪模型倾斜角(图3a)的结果反映的模型边界较为模糊,且明显偏向外侧,而改进倾斜角(图3b)的结果显示出较好的收敛性,其不加峰值约束的欧拉反演结果分别位于图3b和3d,滑动窗口大小选择11×11。计算过程中,因导数计算对噪声较为敏感,因此将各阶导数向上延拓1.6 km以平滑噪声的影响。从计算结果看出,iTilt-Euler法反演的边界位置比Tilt-Euler法的结果更加清晰,但因受场源体异常相互叠加的影响,浅源和深源地质体的结果均出现较多杂解。尤其对深源地质体来讲,因受到浅源高频异常的干扰,邻近浅源体一侧深度解明显偏大,而另一侧则明显偏小。图3e和3f分别为水平总梯度倾斜角及其峰值约束之下的欧拉反演结果。可以看出,约束下的iTilt-Euler反演结果收敛性较好,虚假解明显减少,深度结果分别为1.12±0.01 km、2.28±0.02 km和3.33±0.03 km,误差分别为12%、14%和11%。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 加2%高斯噪声的组合模型欧拉反演结果

a—倾斜角;b—Tilt-Euler法反演结果;c—改进倾斜角;d—iTilt-Euler法反演结果;e—水平总梯度倾斜角;f—水平总梯度倾斜角峰值约束下的iTilt-Euler法反演结果

Fig.3 Results of Euler deconvolution based on the combined model with 2% Gaussian noise

a—tilt angle; b—estimated results from the Tilt-Euler; c—improved tilt angle; d—estimated results from the iTilt-Euler; e—total horizontal derivative of tilt angle; f—estimatedresults fromthe iTilt-Euler under the peak constraint of total horizontal derivative of tilt angle

3 实际数据应用

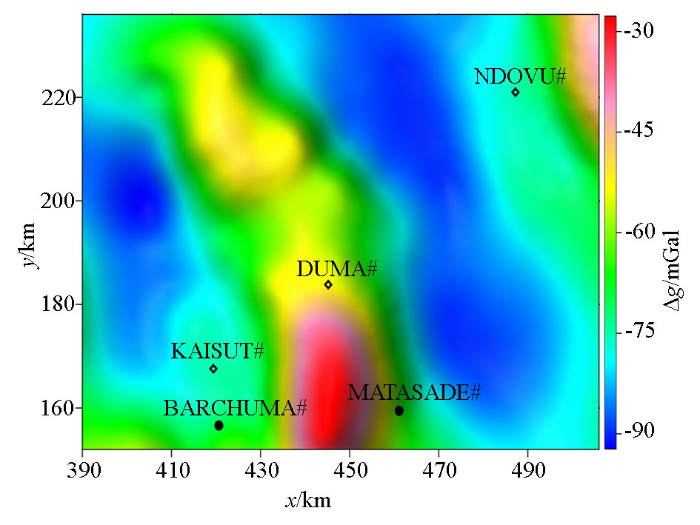
为了验证iTilt-Euler法的实际应用效果,本文采用肯尼亚ANZA盆地某区块的重力数据进行了处理分析。从研究区布格重力异常图(图4)可以看出,重力高、重力低成排相间分布,整体呈NW走向。研究区东北角发育一NW向展布、未闭合的重力高,幅值约为-50×10^-5 m/s²。MATASADE与BARCHUMA之间,向北西延伸为一条带状展布的重力高,有两个重力高中心点,异常最大幅值位于MATASADE以西,约为-30×10^-5 m/s²。DUMA井-MATASADE一线以东至NDOVU井,发育一NW向的重力低,分别在NDOVU井以西和DUMA井东南有两个重力低圈闭中心。此外,研究区西部为一NW向展布的不规则形重力低,该重力低圈闭中心异常值大约为-90×10^-5 m/s²。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 研究区布格重力异常

Fig.4 The map of the Bouguer gravity anomaly in study area

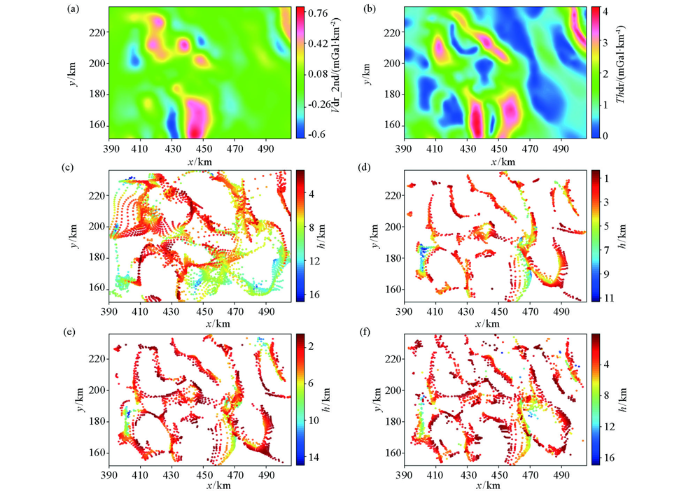
重力异常平面图上的线性梯级带、等值线的规则性扭曲或异常轴的水平错动、串珠状异常等的分布规律为断层结构的解释提供了依据。研究区垂向二阶导数(图5a)和水平总梯度异常(图5b)清晰反映出研究区异常主体呈NW走向,且异常高、低成排相间分布。图5c~e分别为利用传统欧拉反褶积、Tilt-Euler和iTilt-Euler法计算所得的结果,滑动窗口均选择11×11。反演结果表明,Tilt-Euler和iTilt-Euler法所得的结果更为收敛,且解的分布与垂向二阶导数和水平总梯度异常图中断裂识别标志较吻合。解的分布主要呈NW向,其次是NE向,反映了研究区断层的主要展布方向。图5f为采用水平总梯度倾斜角峰值约束下的iTilt-Euler法反演结果,与无约束的iTilt-Euler结果(图5e)相比,由于数据点的减少,欧拉解的连续性有所降低,但是研究区中部的局部小断裂得到了较好的体现,且较深的部分断裂连续性得到增强。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 研究区重力异常欧拉反演结果

a—垂向二阶导数;b—水平总梯度;c—常规欧拉反褶积反演结果(N=0.5);d—Tilt-Euler反演结果;e—iTilt-Euler反演结果;f—约束下的iTilt-Euler法反演结果

Fig.5 Euler deconvolution results of gravity anomalies in the study area

a—second order derivative; b—total horizontal derivative; c—estimated results from conventional Euler deconvolution(N=0.5); d—estimated results fromTilt-Euler method; e—estimated results from iTilt-Euler method; f—estimated results from iTilt-Euler method under the peak constraint

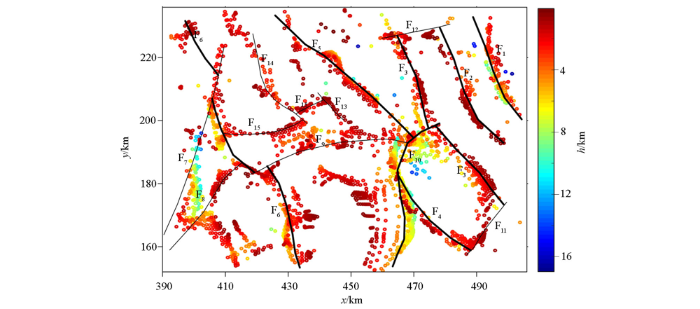
根据ANZA盆地某区块重力数据的欧拉反演结果,结合解在重力异常平面图上的线性梯级带、等值线的规则性扭曲或异常轴的水平错动、串珠状异常等标志带上的分布规律,推断出研究区断裂15条(图6)。这些断裂的走向主要可分为近NW向和近NE向两组,其中,近NW向断裂6条,分别为F₁、F₂、F₃、F₄、F₅、F₆,近NE向断裂6条,为F₇、F₈、F₉、F₁₀、F₁₁、F₁₂。此外,还划分出区域内相互切割的一组次级小断裂F₁₃、F₁₄和F₁₅。断裂走向大体分为NW向和NE向两组,其中以NW向为主,与区域构造走向一致。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 研究区断裂展布

Fig.6 The distribution of fault structure in study area

F₁断裂:该断裂位于研究区东北角,NNW走向。布格重力异常图上反映为断续分布的重力梯级带,垂向二阶导数图上表现为重力高与重力低的过渡带,水平总梯度图上表现为异常的极值连线。约束下的iTilt-Euler法反演结果显示,断裂北西段埋深较浅,约3 km,东南段埋深较深,达到8 km左右。断裂东侧埋深较浅,西侧埋深较深,故倾向近WS向。

F₂-F₅断裂:断裂位于研究区中东部,NNW—NW走向,是研究区东北部凹陷西边界的主控断裂。断裂的重力场异常标志非常明显,布格重力异常图上反映为密集的重力梯级带,垂向二阶导数图上均表现为明显的重力高与重力低的过渡带,在水平总梯度图上表现为异常的极值连线。基于不同数据的欧拉反演解连续性均较好,反映的埋深相对较浅。其中,F₃、F₄、F₅断裂被近NE走向的F₁₀断裂所切断,推测其断裂形成时间可能均早于NE向构造。

F₆断裂:该断裂是研究区西部重力低值区的东部边界断裂,呈NNE走向。布格重力异常图、垂向二阶导数图、水平总梯度图等图件上均表现为明显的断裂构造特征显示。欧拉反演结果显示,断裂西南侧埋深较深,东北侧埋深较浅,故倾向WS。F₆断裂被NE走向的F₇、F₉断裂所切断,因此,推测其断裂形成时间可能早于NE向构造。该断裂深度较大,约6~7 km,为控凹断层,它们控制了西部凹陷内沉积层的厚度和范围。

F₉断裂:该断裂位于研究区中部,呈近EW走向。布格重力异常图上表现为异常等值线扭曲,垂向二阶导数图上表现为两重力高的鞍部,水平总梯度图上表现为异常的极值连线。欧拉反演结果显示,断裂北侧埋深较深,南侧埋深较浅,故倾向N。该断裂连续性较差,且被NW走向的F₆断裂所切割,因此,推测该断裂形成时间可能晚于NW向构造。

F₁₀断裂:该断裂位于研究区东南部,由南端的近SN向NE向延伸。布格重力异常图上反映为断续分布的重力梯级带,垂向二阶导数图上表现为重力高与重力低的过渡带,水平总梯度图上表现为极大值连线。欧拉反演结果显示,该断裂埋深较大,约在6~9 km的范围内。该断裂西北侧埋深较浅,南东侧较深,故倾向SE。该断裂连续性较好,切割了NW走向的F₃、F₄和F₅断裂和NE向的F₉断裂,因此,推测其可能是一条最晚形成、控制区域构造单元东南边界的深大断裂。

据20世纪90年代的少量地震反射剖面^[29,30]资料来看,NW—SE向展布的地堑系是Anza盆地的主导构造,且均截切基底。此外,据前人^[31]对穿过研究区的一条二维地震测线(KAISUT井—NDOVU井一线)的解释说明,研究区前寒武基底深度差异较大,整体呈现东、西两侧凹陷,而中部隆起的特征。东部凹陷基底深度约为10 km,西部凹陷约为7 km,中间隆起仅约3 km。同时,该地震测线的资料也说明研究区NW向正断层非常发育,且截切基底,而大量的次生断裂发育于前寒武结晶基底之上。这一特征与本文欧拉反褶积反演的深度结果一致,研究区NW向基底断裂在东部和西部区域的截切深度较大,约为6~9 km,而中部区域则较浅,约3~4 km左右。

4 结论

iTilt-Euler法不依赖于场源体的构造指数,能快速估算出场源体的边界和深度位置,为位场资料的处理和解释提供了重要的方法手段。相较于Tilt-Euler法,iTilt-Euler法避免了各方向导数求解中存在的“解析奇点”,保证了计算结果的稳定性。同时,本文采用水平总梯度倾斜角峰值约束法,有效约束了反演数据点,使得反演结果更加收敛、准确。模型试算和实际数据应用均反映出,在约束法控制下的iTilt-Euler法的反演结果,由于减少了场源异常相互叠加的影响,不仅有效压制解的发散性,也使得深部场源的位置和深度信息得到了更好的反映。

研究区断裂发育,断裂走向主要可以分为NW向和NE向两组。NW向断裂规模大,延伸距离长,切穿深度大,大多为控制区内构造单元边界的基底断裂。大多NE向断裂规模相对小,它们一般切断NW向断裂,为盖层(沉积层内部)断裂。而在研究区东南部发育的一条近NNE向展布的断裂,同时切割了NW向和NE向断裂,推测其可能是控制区域构造单元东南边界的一条深断裂。

致谢

感谢西安石油大学袁炳强教授提供的重力数据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Thompson D

EULDPH—A new technique for making computer-assisted depth estimates from magnetic data

[J]. Geophysics, 1982, 47(1):31-37.

DOI:10.1190/1.1441278 URL [本文引用: 2]

[2]

Reid A

, Allsop J

, Granser

, et al.

Magnetic interpretation in three dimensions using Euler deconvolution

[J]. Geophysics, 1990, 55(1):80-91.

DOI:10.1190/1.1442774 URL [本文引用: 1]

[3]

姚长利, 管志宁, 吴其斌, 等.

欧拉反演方法分析及实用技术改进

[J]. 物探与化探, 2004, 28(2):150-155.

[本文引用: 4]

Yao C

, Guan Z

, Wu Q

, et al.

An analysis of Euler deconvolution and its improvement

[J]. Geophysical and Geochemical Exploration, 2004, 28(2):150-155.

[本文引用: 4]

[4]

Hsu S

Imaging magnetic sources using Euler’s equation

[J]. Geophysical Prospecting, 2002, 50:15-25.

DOI:10.1046/j.1365-2478.2001.00282.x URL [本文引用: 1]

[5]

Salem

, Ravat

A combined analytic signal and Euler method (AN-EUL) for automatic interpretation of magnetic data

[J]. Geophysics, 2003, 68(6):1952-1961.

DOI:10.1190/1.1635049 URL [本文引用: 2]

[6]

Salem

, Smith

Generalized magnetic tilt-Euler deconvolution

[C]// SEG Expanded Abstracts, 2007: 790-794.

[本文引用: 2]

[7]

范美宁, 江裕标, 张景仙.

不同数据用于欧拉方程的模型计算

[J]. 地球物理学进展, 2008, 23(4):1250-1253.