0 引言
大地极化声子测深技术是由乌克兰科学家尤·阿·博格达诺夫提出的一种被动源地球物理电磁勘探方法,地球内部岩石的应力变化导致岩石产生变形以及破坏断裂,从而产生声发射和电磁辐射,该方法通过测量电磁波辐射强度来研究地球内部结构[1 ] 。大地形变产生的电磁辐射具有较宽的频率范围,理论上,该方法可用于研究大地的地质结构。目前,在国内已经开始进行了一些试验和研究[2 ] 。
大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生。同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂。岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大。1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后。Cook的研究开启了岩石破裂过程的新篇章[4 ] 。华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] 。唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] 。高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏。岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] 。Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] 。龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] 。
对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] 。声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现。20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] 。 Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应。唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] 。张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] 。赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] 。曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] 。Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] 。郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] 。徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] 。王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射。但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] 。
研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] 。震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种。Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] 。刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] 。Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] 。刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] 。李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] 。虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献。
尽管博格达诺夫提出了大地极化声子的概念,国内的研究学者们也进行了实验研究,但其极化机理并不清楚,一般认为这种大地极化声子可能是由大地构造活动(如地震)或人类活动(如页岩气压裂)产生的压电效应所致。本文尝试从大地岩石破碎时的电磁发射过程出发,以压电效应为基础,开展对大地极化声子测深技术的模拟研究,通过岩石破裂的压电应变矩阵和压电本构方程,导出岩石中电磁辐射与外力作用下的变换关系,模拟多种裂隙形态下的电磁辐射效应,分析电磁辐射特征。
1 压电电磁辐射原理
大地极化声子测深技术的原理是机械运动使岩石的应力状态发生变化,岩石因受到挤压产生变形直至破碎,产生极化声子,从而发出电磁信号。这种极化声子可能是由大地构造活动或人类活动产生的压电效应所致。
选择坐标轴x 、y 、z 与晶轴X 、Y 、Z 重合,压电介质的压电应变矩阵[28 ] 为:
(1) [ d ] = d 11 d 12 d 13 d 14 d 15 d 16 d 21 d 22 d 23 d 24 d 25 d 26 d 31 d 32 d 33 d 34 d 35 d 36 ,
式中:d 表示压电应变常数,第一个下标表示所产生电位移的方向(1、2、3分别表示x ,y ,z 方向),第二个下标表示作用力方向(1、2、3、4、5、6分别表示沿x 、y 、z 三个轴方向的应力和垂直于x 、y 、z 三个轴平面(XZ 、YZ 、XY 平面)作用的剪切力)。
在地壳上部,石英占66.4% ,并且是许多岩石的成岩矿物,这为压电效应提供了物质基础,故用石英的压电应变矩阵来代替地壳中含有石英等压电介质的岩石的压电应变矩阵。石英晶体的压电应变常数与其内部结构有关,属于三角晶系32点群。有3个晶轴:x 轴、y 轴和z 轴,当晶体沿x 轴或者y 轴方向受到压力时,晶格变形,产生压电效应;沿z 轴方向受到力时,由于晶格的变形不会引起正负电荷中心的分离,不会产生压电效应。因此,含有石英等压电介质的岩体的压电应变矩阵[29 ] 为:
(2) [ d ] = d 11 d 12 0 d 14 0 0 0 0 0 0 d 25 d 26 0 0 0 0 0 0 。
(3) T 1 = T 0 e - η 0 x e i ( ω 0 t - k 0 x ) ,
式中:ω 为应力波的角频率, T 0 为应力波的初始振幅值,k 0 是应力波的波数,η 0 为应力波的衰减系数。岩石受应力波作用而变形,产生压电效应。根据压电本构方程[30 ] :
(4) D = ε T E + dT S = d T E + s E T
式中:D 为电位移矢量,T 为应力波,E 为外加电场强度, d T 为d 的转置矩阵,ε T 表示应力恒定时的介电常数,s E 表示场强恒定时的弹性柔顺常数。
由式(2)、(3)、(4)可以得到应力场对电位移矢量D 压电 产生压电贡献(不考虑外加电场,即E =0),由于应力波沿x 方向对裂隙施加作用力,在垂直x 轴的平面上产生电荷,因此只需考虑式(2)中的d 11 参数:
(5) D 压电 = d 11 T 1 ,
(6) $\left\{\begin{array}{l} \nabla \times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t} \\ \nabla \times \boldsymbol{H}=-\frac{\partial \boldsymbol{D}}{\partial t}+J_{c}, \\ \nabla \cdot \boldsymbol{E}=0 \\ \nabla \cdot \boldsymbol{D}=\rho \end{array}\right.$
(7) D = εE , B = μH 。
式中:B 、 H 、D 和E 分别为电磁场的磁感应强度、磁场强度、电位移矢量和电场强度;μ 为磁导率;Jc 为传导电流密度,在岩体中设Jc =0。
(8) $\nabla^{2} E-\mu \varepsilon \frac{\partial^{2} E}{\partial t^{2}}=\mu \frac{\partial^{2} D}{\partial t^{2}},$
式中:k 是电磁波的复波数,σ 为电导率,ω 为电磁波的角频率。
将式(5)代入式(8),可得应力波作用下岩石产生电磁辐射的方程:
(9) ∂ 2 E ∂ x 2 - με ∂ 2 E ∂ t 2 = μ d 11 ∂ 2 T ∂ t 2
(10) μ d 11 ∂ 2 T ∂ t 2 = - μ d 11 ω 0 2 T 0 e - η 0 x e i ( ω 0 t - k 0 x ) 。
由于电磁波在岩石介质中具有色散特性,将电磁波用复数形式表示,设:
(11) E = E e e i ( ωt ) ,
(12) ∂ 2 E e ∂ x 2 + ( με ω 2 ) E e = - μ d 11 ω 0 2 T 0 e - η 0 x e i ( ω 0 t - k 0 x ) e i ( ωt ) 。
(13) E e = - d 11 ω 0 2 T 0 e - η 0 x 1 e i ( ω 0 - ω ) t η 0 2 + 2 i k 0 η 0 + με ω 2 - k 0 2 e - ( η 0 + i k 0 ) x 。
(14) E = - d 11 ω 0 2 T 0 e - η 0 x 1 e i ( ω 0 - ω ) t η 0 2 + 2 i k 0 η 0 + με ω 2 - k 0 2 e - ( η 0 + i k 0 ) x · e i ωt 。
电磁辐射信号在岩石介质中传播时会发生衰减及相变,引入e-i kr [31 ] :
(15) k = ( ω 2 με - i ωμσ ) = β - i α ,
(16) α = ω με 2 1 + σ ωε 2 - 1 ,
(17) β = ω με 2 1 + σ ωε 2 + 1 。
式中:k 为复波数,α 是电磁波的衰减系数,β 为电磁波的相位系数,σ 为大地介质的电导率,ω 为电磁波的角频率,r 表示电磁波传播的距离。应力波作用下,岩石产生电磁辐射的传播方程为:
(18) E = - d 11 ω 0 2 T 0 e - η 0 x 1 e i ( ω 0 - ω ) t η 0 2 + 2 i k 0 η 0 + με ω 2 - k 0 2 e - ( η 0 + i k 0 ) x · e i ( ωt - kr ) 。
2 发射频率
Rabinovitch等通过大量实验发现岩石产生的电磁辐射频率受裂纹宽度的限制,频率与裂纹宽度成反比,并给出了电磁辐射频率与裂纹宽度之间的关系[32 ] :
(19) ω = π v R b ,
(20) f = ω 2 π ,
(21) v R = 0.87 + 1.12 μ b 1 + μ b · E T 2 ( 1 + μ b ) ρ 。
式中:f 为频率, μ b 为泊松比,E T 为弹性模量,ρ 为密度。可以得到岩石产生的电磁辐射频率与裂纹宽度的关系:
(22) f = 1 2 b 0.87 + 1.12 μ b 1 + μ b · E T 2 ( 1 + μ b ) ρ 。
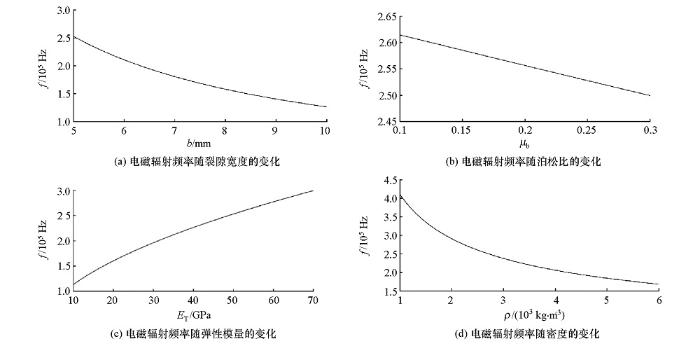
显然电磁辐射频率与裂纹宽度及岩石的物理性质有关。含石英类岩石的泊松比范围为0.10~0.40,弹性模量一般为10~100 GPa,密度为2.6~2.9 kg/m3 ,故取泊松比μ b =0.25,密度ρ =2.65×103 kg/m3 ,弹性模量E T =50 GPa。图1 a为根据式(22)得到的电磁辐射频率随裂纹宽度的变化曲线,可以看到岩石破裂产生的电磁辐射频率较高,一般大于105 Hz,同时电磁辐射频率随裂纹宽度的增大呈指数减小。
图1
图1
电磁辐射频率随岩石参数的变化
Fig.1
Variation curve of electromagnetic radiation frequency with rock parameters
取裂隙宽度b =0.005 m,密度与弹性模量与上述相同,得到电磁辐射频率随泊松比的变化如图1 b所示,可以看到电磁辐射频率随泊松比的增大呈线性衰减。类似地可以得到电磁辐射频率随弹性模量与密度的变化如图1 c、d所示,可以看到电磁辐射频率随弹性模量的增大而增大,随密度的增大而减小。比较图1 可以看到电磁辐射频率受泊松比和弹性模量影响较小,受裂隙宽度和密度影响较大。
3 数值模拟与分析
通过对裂隙单模型和组合模型的电磁辐射响应特征的数值模拟,讨论基于压电效应的大地极化声子测深技术的有效性。
3.1 单模型
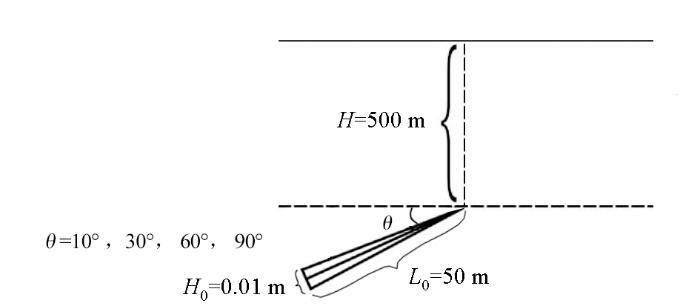
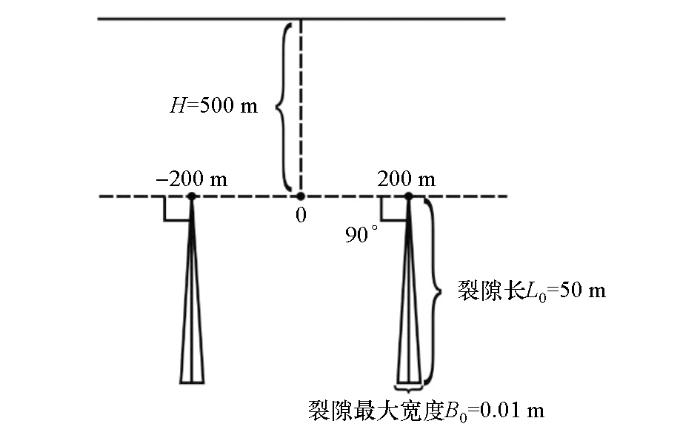
设地下电阻率为1 000 Ω·m的均匀半空间中存在1个三角形裂隙( 图2 ),倾角θ 分别为10°、30°、60°和90°;裂隙埋深H =500 m,裂隙长度L 0 =50 m,最大宽度B 0 =0.01 m。应力波作用时间t =1 s,应力波角频率ω 0 =(2π×10) rad/s,应力波波数k 0 =0.01 m-1 ,衰减系数η 0 =0.05。磁导率为真空磁导率μ =4π×10-7 H/m。根据含石英类岩石的介电常数为(4~9)×8.85×10-12 F/m和压电应变常数范围为(0.5~5)×10-13 C/N,故取介电常数为ε =5×8.85×10-12 F/m,压电应变常数d 11 =10-13 C/N。泊松比μ b =0.25,密度ρ =2.65×103 kg/m3 ,弹性模量E T =50 GPa,电导率σ =0.001 S/m。设有一个水平方向的应力波,其作用力T 0 =107 Pa,且电磁辐射由应力垂直于裂隙方向的分力产生。
图2
图2
倾斜裂隙模型示意
Fig.2
Schematic diagram of inclined fracture model
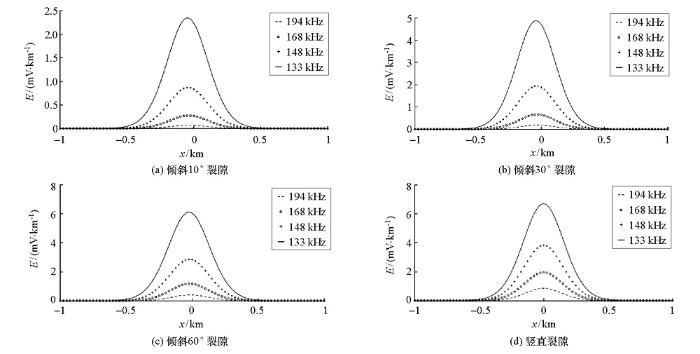
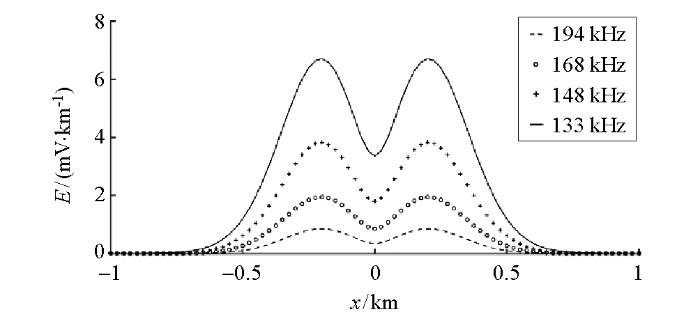
图3 是岩石裂隙电磁发射的地表电场幅值。由图3 a可以看到:电场幅值曲线的变化趋势为中间高两边低,电磁发射频率越低,电场幅值就越大;随着频率的增加,幅值快速下降;电场幅值的极值点位置和大小随频率变化,频率越低,极值点越大,越偏离中心(裂隙顶点在地表的投影)。
图3
图3
裂隙电场幅值随倾角变化
Fig.3
The electric field amplitude of the fissure varies with the inclination angle
将不同产状的裂隙电场幅值图进行对比,可以发现倾斜程度越大(即倾角越小)的裂隙,电场(从低频到高频)的幅值和极值点越小,极值点偏离坐标轴中心也越远。电场幅值的位置以及变化趋势能够反映出裂隙的位置和产状。极值点的连线方向与裂隙的倾斜方向相反;连线方向与地表铅垂方向的夹角反映了裂隙的倾斜度的大小。夹角越大,裂隙的倾斜度越大。通过曲线的频率能够定性分析裂隙的宽度变化。
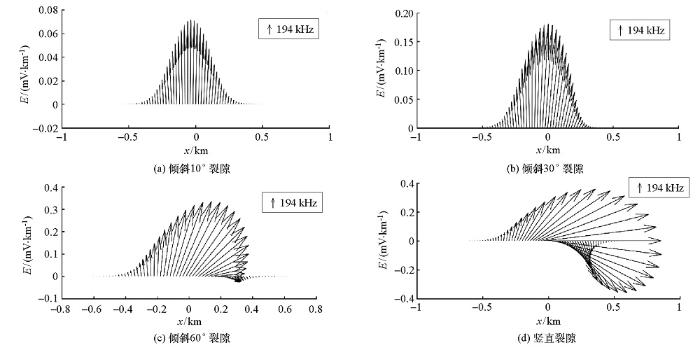
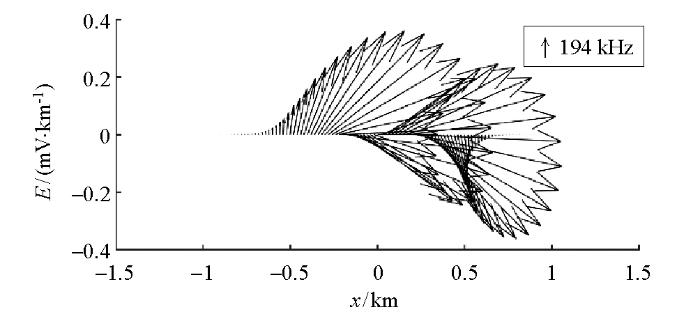
图4 分别是不同倾角的裂隙的电场矢量图(z 轴向上为正方向, x 轴向右为正方向)。以图4 d为例,电场的矢量方向沿一个方向变化(顺时针方向),矢量幅值变化趋势为增大—降低—增大—降低,在正负方向上各拥有一个极值;在z 轴正方向上极值与负方向上的极值相近。
图4
图4
裂隙电场矢量随倾角变化
Fig.4
Crack electric field vector changes with inclination angle
将不同产状的裂隙电场矢量图进行对比,可以发现竖直裂隙的z 轴正方向极值与负方向极值相同。倾斜程度越大(即倾角越小)的裂隙,其z 轴负方向上的极值相比正方向也就越小,直到30°的裂隙的负值消失。根据电场矢量图所显示的地表电场的幅值、方向及变化趋势,能够大致判断出产生电磁辐射的电场源的产状和位置以及深度。
3.2 组合模型
设地下电阻率为1 000 Ω·m的均匀半空间,存在2个分开的竖直的完全一致的三角形裂隙( 图5 ),裂隙埋深H =500 m,长度L 0 =50 m,其他参数同上。2个裂隙都受到水平方向的应力波T 0 =107 Pa的作用。
图5
图5
组合裂隙模型示意
Fig.5
Schematic diagram of combined fracture model
从图6 可以看到:电场幅值由双峰组成,频率越低,曲线的幅值越大,且所有频率电磁辐射幅值的极值点都位于x =-200 m或x =200 m线上。从图7 可以看到,电场的矢量并不是沿一个方向变化,出现了重复的矢量方向,矢量在z 轴正方向上有2个极值,左边极值大于右边;在负方向上也有2个极值,但是右边极值大于左边。通过图6 和图7 ,能够大致判断出组合裂隙的位置。
图6
图6
组合裂隙电场幅值
Fig.6
The electric field amplitude of the combined fracture
图7
图7
组合裂隙电场矢量
Fig.7
Electric field vector of combined fracture
通过对比单裂隙模型可以发现组合裂隙与单裂隙的差别:在电场幅值图中单异常体是单峰,而组合裂隙是多峰,并有波谷存在;在电场矢量图中虽然单裂隙电场方向是沿顺时针变化的,而组合裂隙的电场方向变化趋势会出现转变,单裂隙不会出现重复的矢量方向,且只有一个极大值和一个极小值,但组合裂隙有多个极大值和多个极小值。运用该方法能够分辨组合裂隙与单裂隙,同时能够大致判断组合裂隙的位置。
4 结论
本文从岩石的压电效应出发,推导出在均匀半空间情况下岩石的电磁辐射的产生和传播方程。岩石破裂产生的电磁辐射频率与裂隙的尺度及波的弹性参数有关,裂纹宽度越大,产生的电磁辐射频率越低,但一般高于105 Hz;同时,电磁辐射频率还会受到岩石的泊松比、弹性模量与密度的影响。
对不同产状及形态的裂隙模拟表明,岩石破裂产生的电磁辐射响应特征明显,在裂隙的上方有极值存在,极值大小随裂隙的尺度及频率变化,并且可以通过多个频率的极值变化特征推断裂隙的产状,利用其电磁辐射响应及矢量图可以识别裂隙的数量。模拟研究表明基于岩石压电效应为基础的大地极化声子测深技术具有潜在的应用价值。
参考文献
View Option
[1]
胥值礼 , 孟庆敏 , 崔志强 , 等 . 大地极化声子测深技术的调研与试用
[J]. 物探与化探 , 2014 , 38 (4 ):758 -763 .
[本文引用: 1]
Xu Z L Meng Q M Cui Z Q , et al . The investigation and trial utilization of geopolariton sensing technology
[J]. Geophysical and Geochemical Exploration , 2014 , 38 (4 ):758 -763 .
[本文引用: 1]
[2]
闫新智 , 雷俊杰 . 大地极化声子测深方法在延长油田某区块石油勘探方面的实验
[C]// 中国石油石化企业信息化技术交流会论文集 , 2011 .
[本文引用: 1]
Yan X Z Lei J J . An experiment on the application of the method of geodetic polariton exploration technology in oil exploration of a block in Yanchang oilfield
[C]// Paper collection of China Petroleum and petrochemical enterprise information technology exchange meeting , 2011 .
[本文引用: 1]
[3]
薛承瑾 . 页岩气压裂技术现状及发展建议
[J]. 石油钻探技术 , 2011 , 39 (3 ):24 -29 .
[本文引用: 1]
Xue C J . Technical status and development proposals of shale gas fracturing
[J]. Petroleum Drilling Techniques , 2011 , 39 (3 ):24 -29 .
[本文引用: 1]
[4]
Cook N G W . The failure of rock
[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts , 1965 , 2 (4 ):389 -403 .
[本文引用: 1]
[5]
华保钦 . 构造应力场、地震泵和油气运移
[J]. 沉积学报 , 1995 , 13 (2 ):77 -85 .
[本文引用: 1]
Hua B Q . Stress field, seismic pumping and oil-gas migration
[J]. Acta Sedimentologica Sinica , 1995 , 13 (2 ):77 -85 .
[本文引用: 1]
[6]
唐志强 , 李皋 , 石祥超 , 等 . 岩石单轴冲击加载破碎特征分析
[J]. 应用力学学报 , 2019 , 36 (5 ):1076 -1081,1258 .
[本文引用: 1]
Tang Z Q Li G Shi X C , et al . Analysis of rock fragmentation characteristics under uniaxial impact loading
[J]. Chinese Journal of Applied Mechanics , 2019 , 36 (5 ):1076 -1081,1258 .
[本文引用: 1]
[7]
高美奔 , 李天斌 , 陈国庆 , 等 . 工程温压内花岗岩破裂特征与机理分析
[J]. 科学技术与工程 , 2018 , 18 (15 ):13 -18 .
[本文引用: 1]
Gao M B Li T B Chen G Q , et al . The Analysis on Fracture Characteristics and Mechanism of Granite under Engineering Temperature and Pressure
[J]. Science Technology and Engineering , 2018 , 18 (15 ):13 -18 .
[本文引用: 1]
[8]
Cress G O Brady B T Rowell G A . Sources of electromagnetic radiation from fracture of rock samples in laboratory
[J]. Geophysical Research Letters , 1987 , 14 (4 ):331 -334 .
DOI:10.1029/GL014i004p00331
URL
[本文引用: 1]
[9]
龚强 , 胡祥云 , 张胜业 , 等 . 岩石破裂电磁辐射频率与弹性参数的关系
[J]. 地球物理学报 , 2006 , 49 (5 ):1523 -1528 .
[本文引用: 1]
Gong Q Hu X Y Zhang S Y , et al . Relationship between frequency of electromagnetic radiation induced by rock fracture and the elastic parameters
[J]. Chinese Journal of Geophysics , 2006 , 49 (5 ):1523 -1528 .
[本文引用: 1]
[10]
张孟举 . 脆性岩石受载破碎声发射与电磁辐射特性试验研究
[D]. 湘潭: 湖南科技大学 , 2017 .
[本文引用: 1]
Zhang M J . A study on characteristics of acoustic emission and electromagnetic emission in brittle rock fragmentation under different load
[D]. Xiangtan: Hunan University of Science and Technology , 2017 .
[本文引用: 1]
[11]
聂百胜 , 何学秋 , 王恩元 , 等 . 煤体剪切破坏过程电磁辐射与声发射研究
[J]. 中国矿业大学学报 , 2002 , 31 (6 ):65 -67 .
[本文引用: 1]
Nie B S He X Q Wang E Y , et al . Study on electromagnetic radiation and acoustic emission in shearing process of coal
[J]. Journal of China University of Mining & Technology , 2002 , 31 (6 ):65 -67 .
[本文引用: 1]
[12]
万国香 . 应力波作用下岩石电磁辐射与声发射特性研究
[D]. 长沙:中南大学 , 2008 .
[本文引用: 1]
Wan G X . Study on the characteristics of the electromagnetic emission and acoustic emission in rock under stress wave
[D]. Changsha: Central South University , 2008 .
[本文引用: 1]
[13]
Obert L . Use of subaudible noises for the prediction of rock bursts
[R]. U.S. Bureau of Mines , 1941 :1 -4 .
[本文引用: 1]
[14]
唐春安 . 岩石声发射规律数值模拟初探
[J]. 岩石力学与工程学报 , 1997 ,(4 ):75 -81 .
[本文引用: 1]
Tang C A . Numerical simulation of ae in rock failure
[J]. Chinese Journal of Rock Mechanics and Engineering , 1997 ,(4 ):75 -81 .
[本文引用: 1]
[15]
张国凯 , 李海波 , 王明洋 , 等 . 脆性岩石应力-应变全过程声学特征演化规律
[J]. 中南大学学报:自然科学版 , 2019 , 50 (8 ):1971 -1980 .
[本文引用: 1]
Zhang G K Li H B Wang M Y , et al . Evolution rule of acoustic characteristics of brittle rocks during whole stress-strain process
[J]. Journal of Central South University:Science and Technology , 2019 , 50 (8 ):1971 -1980 .
[本文引用: 1]
[16]
赵伏军 , 李玉 , 陈珂 , 等 . 岩石破碎声发射和电磁辐射特征试验研究
[J]. 地下空间与工程学报 , 2019 , 15 (2 ):345 -351,364 .
[本文引用: 1]
Zhao F J Li Y Chen K , et al . Experimental research on characteristics of acoustic electrical signal of rock fragmentation
[J]. Chinese Journal of Underground Space and Engineering , 2019 , 15 (2 ):345 -351,364 .
[本文引用: 1]
[17]
曹惠馨 , 钱书清 , 吕智 . 岩石破裂过程中超长波段的电、磁信号和声发射的实验研究
[J]. 地震学报 , 1994 , 16 (2 ):235 -241 .
[本文引用: 1]
Cao H Q Qian S Q Lyu Z . Experimental study on Electrical and magnetic signals and acoustic emission of ultra long wave band in the process of rock fracture
[J]. Acta Seismologica Sinica , 1994 , 16 (2 ):235 -241 .
[本文引用: 1]
[18]
Yamada I Masuda K Mizutani H . Electromagnetic and acoustic emission associated with rock fracture
[J]. Physics of the Earth and Planetary Interiors , 1989 , 57 (1-2 ):1 -168 .
DOI:10.1016/0031-9201(89)90207-0
URL
[本文引用: 1]
[19]
郭自强 , 郭子祺 , 钱书清 , 等 . 岩石破裂中的电声效应
[J]. 地球物理学报 , 1999 , 42 (1 ):74 -83 .
[本文引用: 1]
Guo Z Q Guo Z Q Qian S Q , et al . Electro-acoustic effect in rock fracturing
[J]. Chinese Journal of Geophysics , 1999 , 42 (1 ):74 -83 .
[本文引用: 1]
[20]
徐为民 , 童芜生 , 吴培稚 . 岩石破裂过程中电磁辐射的实验研究
[J]. 地球物理学报 , 1985 , 28 (2 ):181 -190 .
[本文引用: 1]
Xu W M Tong W S Wu P Z . Experimental study of electromagnetic emission during rock fracture
[J]. Chinese Journal of Geophysics , 1985 , 28 (2 ):181 -190 .
[本文引用: 1]
[21]
王恩元 , 何学秋 . 煤岩变形破裂电磁辐射的实验研究
[J]. 地球物理学报 , 2000 , 43 (1 ):131 -137 .
[本文引用: 1]
Wang E Y He X Q . An experimental study of the electromagnetic emission during the deformation and fracture of coal or rock
[J]. Chinese Journal of Geophysics , 2000 , 43 (1 ):131 -137 .
[本文引用: 1]
[22]
Yoshida S Manjgaladze P Zilpimiani D , et al. Electromagnetic emissions associated with frictional sliding of rock [C]// Hayakawa M, Fujinawa Y(Eds). Electromagnetic Phenomena related to earthquake prediction terra. Tokyo : Scientific Publishing Company , 1994 :307 -322 .
[本文引用: 1]
[23]
Gokhberg M B . Static model of distributed emitters
[J]. Transactions(Doklady) of USSR academy of sciences: Earth Science Section , 1988 , 302 (5 ):1 -3 .
[本文引用: 1]
[24]
刘煜洲 , 刘因 , 王寅生 , 等 . 岩石破裂时电磁辐射的影响因素和机理
[J]. 地震学报 , 1997 , 19 (4 ):83 -90 .
[本文引用: 1]
Liu Y Z Liu Y Wang Y S , et al . Influencing factors and mechanism of electromagnetic radiation in rock fracture
[J]. Acta Seismologica Sinica , 1997 , 19 (4 ):83 -90 .
[本文引用: 1]
[25]
Huang Q H . One possible generation mechanism of co-seismic electric signals
[J]. The Japan Academy , 2002 , 78 (7 ).
[本文引用: 1]
[26]
刘志祥 . 冲击载荷作用下花岗岩产生的电磁辐射研究
[D]. 北京:北京理工大学 , 2017 .
[本文引用: 1]
Liu Z X . Electromagnetic emissions of granite induced by the impact loads
[D]. Beijing: Beijing Institute of Technology , 2017 .
[本文引用: 1]
[27]
李夕兵 , 古德生 . 应力波和电磁波在岩体中相互耦合的研究
[J]. 中南矿冶学院学报 , 1992 , 23 (8 ):260 -266 .
[本文引用: 1]
Li X B Gu D S . The investigation on the couplings of stress wave and electromagnetic wave in rocks
[J]. Journal of Central South University , 1992 , 23 (8 ):260 -266 .
[本文引用: 1]
[28]
王秀琨 , 王寅生 . 岩石压电性
[J]. 物探与化探 , 1985 , 9 (4 ):274 -280 .
[本文引用: 1]
Wang X K Wang Y S . Piezoelectricity of rocks
[J]. Geophysical and Geochemical Exploration , 1985 , 9 (4 ):274 -280 .
[本文引用: 1]
[29]
宋道仁 , 肖鸣山 . 压电效应及其应用 [M]. 北京 : 科学普及出版社 , 1987 .
[本文引用: 1]
Song D R Xiao M S Piezoelectric effect and its application [M]. Beijing : Science and Technology of China Press , 1987 .
[本文引用: 1]
[30]
奥尔特 . 固体中的声场和波 [M]. 孙承平, 译. 北京 : 科学出版社 , 1982 .
[本文引用: 1]
Auld B A Acoustic fields and waves in solids [M]. Sun C P. Beijing : Science Press , 1982 .
[本文引用: 1]
[31]
杨儒贵 . 电磁场与电磁波 [M]. 北京 : 高等教育出版社 , 2010 :205 -208 .
[本文引用: 1]
Yang R G Electromagnetic fields and waves [M]. Beijing : Higher Education Press , 2010 :205 -208 .
[本文引用: 1]
[32]
Rabinovitch A Frid V Bahat D . Parametrization of electromagnetic radiation pulses obtained by triaxial fracture of granite samples
[J]. Philosophical Magazine Letters , 1998 , 77 (5 ):289 -293 .
DOI:10.1080/095008398178444
URL
[本文引用: 1]
[33]
李夕兵 , 万国香 , 周子龙 . 岩石破裂电磁辐射频率与岩石属性参数的关系
[J]. 地球物理学报 , 2009 , 52 (1 ):253 -259 .
[本文引用: 1]
Li X B Wan G X Zhou Z L . The relation between the frequency of electromagnetic radiation (EMR) induced by rock fracture and attribute parameters of rock masses
[J]. Chinese Journal of Geophysics , 2009 , 52 (1 ):253 -259 .
[本文引用: 1]
大地极化声子测深技术的调研与试用
1
2014
... 大地极化声子测深技术是由乌克兰科学家尤·阿·博格达诺夫提出的一种被动源地球物理电磁勘探方法,地球内部岩石的应力变化导致岩石产生变形以及破坏断裂,从而产生声发射和电磁辐射,该方法通过测量电磁波辐射强度来研究地球内部结构[1 ] .大地形变产生的电磁辐射具有较宽的频率范围,理论上,该方法可用于研究大地的地质结构.目前,在国内已经开始进行了一些试验和研究[2 ] . ...
大地极化声子测深技术的调研与试用
1
2014
... 大地极化声子测深技术是由乌克兰科学家尤·阿·博格达诺夫提出的一种被动源地球物理电磁勘探方法,地球内部岩石的应力变化导致岩石产生变形以及破坏断裂,从而产生声发射和电磁辐射,该方法通过测量电磁波辐射强度来研究地球内部结构[1 ] .大地形变产生的电磁辐射具有较宽的频率范围,理论上,该方法可用于研究大地的地质结构.目前,在国内已经开始进行了一些试验和研究[2 ] . ...
大地极化声子测深方法在延长油田某区块石油勘探方面的实验
1
2011
... 大地极化声子测深技术是由乌克兰科学家尤·阿·博格达诺夫提出的一种被动源地球物理电磁勘探方法,地球内部岩石的应力变化导致岩石产生变形以及破坏断裂,从而产生声发射和电磁辐射,该方法通过测量电磁波辐射强度来研究地球内部结构[1 ] .大地形变产生的电磁辐射具有较宽的频率范围,理论上,该方法可用于研究大地的地质结构.目前,在国内已经开始进行了一些试验和研究[2 ] . ...
大地极化声子测深方法在延长油田某区块石油勘探方面的实验
1
2011
... 大地极化声子测深技术是由乌克兰科学家尤·阿·博格达诺夫提出的一种被动源地球物理电磁勘探方法,地球内部岩石的应力变化导致岩石产生变形以及破坏断裂,从而产生声发射和电磁辐射,该方法通过测量电磁波辐射强度来研究地球内部结构[1 ] .大地形变产生的电磁辐射具有较宽的频率范围,理论上,该方法可用于研究大地的地质结构.目前,在国内已经开始进行了一些试验和研究[2 ] . ...
页岩气压裂技术现状及发展建议
1
2011
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
页岩气压裂技术现状及发展建议
1
2011
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
The failure of rock
1
1965
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
构造应力场、地震泵和油气运移
1
1995
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
构造应力场、地震泵和油气运移
1
1995
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
岩石单轴冲击加载破碎特征分析
1
2019
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
岩石单轴冲击加载破碎特征分析
1
2019
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
工程温压内花岗岩破裂特征与机理分析
1
2018
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
工程温压内花岗岩破裂特征与机理分析
1
2018
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
Sources of electromagnetic radiation from fracture of rock samples in laboratory
1
1987
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
岩石破裂电磁辐射频率与弹性参数的关系
1
2006
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
岩石破裂电磁辐射频率与弹性参数的关系
1
2006
... 大地构造运动(如地震)会导致地球内部应力场发生巨大变化,造成岩石中断裂和裂隙产生.同样,由于页岩储层的低孔和极低基质渗透率的特点,页岩气的开发主要采用压裂技术,页岩气通常含有天然裂缝,一般会因为胶结而封闭,这些天然裂缝容易在压裂中破裂[3 ] ,这个过程也会造成岩石的破裂.岩石破裂是指岩石在一定的应力条件下,岩石中裂纹开始萌生或者扩大.1966年Cook通过实验研究了岩石的应力—应变曲线,岩石的失稳破裂并非发生在峰值强度点,而是在峰值载荷后.Cook的研究开启了岩石破裂过程的新篇章[4 ] .华保钦归纳了岩石破裂的3个应力场条件:莫尔圆直径增大;异常压力发育时,造成一定深度下孔隙流体压力与上覆负荷之比增大,有效应力减小;最小主应力为张力,最大主应力与最小主应力的大小差距小[5 ] .唐志强等使用分离式SHPB装置进行岩石动力学实验,发现火山碎屑岩以劈裂破坏为主,砂岩以压碎破坏为主[6 ] .高美奔等采用统计方法对不同实验条件下花岗岩的宏观破裂特征进行分析,发现低温低压、低温高压和高温高压时岩样以剪切破坏为主,高温低压时为张拉破坏.岩样性能主要受围压影响,温度对岩样破裂方式有一定影响[7 ] .Glynn O.Cress等通过单轴压缩实验,记录到岩石破裂时产生的电磁辐射[8 ] .龚强等利用张开位移法研究了岩石产生的电磁辐射频率与岩石弹性参数之间的关系,表明电磁辐射频率除了与试件的尺寸有关外,还与岩石的弹性参数有关[9 ] . ...
脆性岩石受载破碎声发射与电磁辐射特性试验研究
1
2017
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
脆性岩石受载破碎声发射与电磁辐射特性试验研究
1
2017
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
煤体剪切破坏过程电磁辐射与声发射研究
1
2002
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
煤体剪切破坏过程电磁辐射与声发射研究
1
2002
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
应力波作用下岩石电磁辐射与声发射特性研究
1
2008
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
应力波作用下岩石电磁辐射与声发射特性研究
1
2008
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
Use of subaudible noises for the prediction of rock bursts
1
1941
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石声发射规律数值模拟初探
1
1997
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石声发射规律数值模拟初探
1
1997
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
脆性岩石应力-应变全过程声学特征演化规律
1
2019
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
脆性岩石应力-应变全过程声学特征演化规律
1
2019
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破碎声发射和电磁辐射特征试验研究
1
2019
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破碎声发射和电磁辐射特征试验研究
1
2019
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂过程中超长波段的电、磁信号和声发射的实验研究
1
1994
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂过程中超长波段的电、磁信号和声发射的实验研究
1
1994
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
Electromagnetic and acoustic emission associated with rock fracture
1
1989
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂中的电声效应
1
1999
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂中的电声效应
1
1999
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂过程中电磁辐射的实验研究
1
1985
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
岩石破裂过程中电磁辐射的实验研究
1
1985
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
煤岩变形破裂电磁辐射的实验研究
1
2000
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
煤岩变形破裂电磁辐射的实验研究
1
2000
... 对于岩石中电磁辐射产生的机制,许多学者提出了基于实验的观点,认为岩石产生的电磁辐射与声发射有关[10 ,11 ,12 ] .声发射是指岩石变形和破裂过程中以弹性波形式释放的应变能现象,声发射是岩石变形和破裂的直接体现.20世纪30年代,Obert L等发现岩石破裂的声发射现象[13 ] . Kaiser观察到金属锌、铜、铝及铅都有声发射现象,并发现了声发射的不可逆效应——Kaiser效应.唐春安通过模拟实验得到了岩石声发射的3种基本模式:主震型、前震-主震-余震型、群震型[14 ] .张国凯等采用岩石加载系统获得脆性花岗岩单轴压缩全应力—应变曲线,同步测试声发射和超声波变化,研究了声发射随岩石破裂的变化规律[15 ] .赵伏军等进行了刀具静力侵入花岗岩破碎实验,发现刀具静力侵入岩石破碎的过程中,声发射和电磁辐射有着很好的正相关性[16 ] .曹惠馨等通过实验发现电磁辐射与声发射的最大值在时间上对应的约占70%,认为岩石中的电磁辐射信号主要是由岩石破裂引起,除此之外可能还与压电效应等有关[17 ] .Yamada等进行了岩石破裂电磁辐射与声发射的实验,发现电磁辐射的起始时间与声发射的起始时间一致,并且拉伸裂纹比剪切裂纹产生电磁辐射的效率更高,认为裂纹是产生电磁辐射的必要条件[18 ] .郭自强等通过实验发现声发射与电磁辐射的关系具有多样性,既有伴随声发射的电磁辐射,也有不伴随声发射的电磁辐射,认为岩石破裂产生的电磁辐射应来源于多种机制[19 ] .徐为民等发现岩石破裂时,电磁脉冲与声发射事件并不能完全一一对应,认为电磁辐射直接由岩石破碎产生[20 ] .王恩元等进行了煤体受载变形破裂的实验研究,结果表明煤体变形破裂时能够产生电磁辐射.但电磁辐射信号较声发射信号丰富,认为电磁辐射与煤体的变形破裂过程相关[21 ] . ...
1
1994
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
Static model of distributed emitters
1
1988
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
岩石破裂时电磁辐射的影响因素和机理
1
1997
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
岩石破裂时电磁辐射的影响因素和机理
1
1997
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
One possible generation mechanism of co-seismic electric signals
1
2002
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
冲击载荷作用下花岗岩产生的电磁辐射研究
1
2017
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
冲击载荷作用下花岗岩产生的电磁辐射研究
1
2017
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
应力波和电磁波在岩体中相互耦合的研究
1
1992
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
应力波和电磁波在岩体中相互耦合的研究
1
1992
... 研究者认为震电效应可能是引起岩石中产生电磁辐射的原因之一[22 ] .震电效应是指地震波和电磁波能量的耦合与转换,即机械力与电磁力的耦合,压电效应是其中的一种.Gokhberg认为岩石的压电效应等力电现象是岩石在受载情况下,由分离电荷张弛产生的电磁辐射效应[23 ] .刘煜洲等认为岩石破裂的低频电磁辐射是由压电效应产生的[24 ] .Huang从压电效应与断层位错理论模型出发,解释了同震电磁辐射信号的产生机制[25 ] .刘志祥研究了冲击载荷作用下花岗岩产生的电磁辐射,分析了花岗岩产生电磁辐射的压电效应和断裂动力学机理[26 ] .李夕兵等认为压电效应是岩石产生电磁辐射的原因,并从压电效应出发,阐明了应力波和电磁波的耦合机制,解释了地震和岩石破碎产生的声、光、电现象[27 ] .虽然目前学界对于岩石破碎产生电磁辐射的机制还不能完全了解,但都不否认压电效应对于岩石产生电磁辐射的贡献. ...
岩石压电性
1
1985
... 选择坐标轴x 、y 、z 与晶轴X 、Y 、Z 重合,压电介质的压电应变矩阵[28 ] 为: ...
岩石压电性
1
1985
... 选择坐标轴x 、y 、z 与晶轴X 、Y 、Z 重合,压电介质的压电应变矩阵[28 ] 为: ...
1
1987
... 在地壳上部,石英占66.4% ,并且是许多岩石的成岩矿物,这为压电效应提供了物质基础,故用石英的压电应变矩阵来代替地壳中含有石英等压电介质的岩石的压电应变矩阵.石英晶体的压电应变常数与其内部结构有关,属于三角晶系32点群.有3个晶轴:x 轴、y 轴和z 轴,当晶体沿x 轴或者y 轴方向受到压力时,晶格变形,产生压电效应;沿z 轴方向受到力时,由于晶格的变形不会引起正负电荷中心的分离,不会产生压电效应.因此,含有石英等压电介质的岩体的压电应变矩阵[29 ] 为: ...
1
1987
... 在地壳上部,石英占66.4% ,并且是许多岩石的成岩矿物,这为压电效应提供了物质基础,故用石英的压电应变矩阵来代替地壳中含有石英等压电介质的岩石的压电应变矩阵.石英晶体的压电应变常数与其内部结构有关,属于三角晶系32点群.有3个晶轴:x 轴、y 轴和z 轴,当晶体沿x 轴或者y 轴方向受到压力时,晶格变形,产生压电效应;沿z 轴方向受到力时,由于晶格的变形不会引起正负电荷中心的分离,不会产生压电效应.因此,含有石英等压电介质的岩体的压电应变矩阵[29 ] 为: ...
1
1982
... 式中:ω 为应力波的角频率, T 0 为应力波的初始振幅值,k 0 是应力波的波数,η 0 为应力波的衰减系数.岩石受应力波作用而变形,产生压电效应.根据压电本构方程[30 ] : ...
1
1982
... 式中:ω 为应力波的角频率, T 0 为应力波的初始振幅值,k 0 是应力波的波数,η 0 为应力波的衰减系数.岩石受应力波作用而变形,产生压电效应.根据压电本构方程[30 ] : ...
1
2010
... 电磁辐射信号在岩石介质中传播时会发生衰减及相变,引入e-i kr [31 ] : ...
1
2010
... 电磁辐射信号在岩石介质中传播时会发生衰减及相变,引入e-i kr [31 ] : ...
Parametrization of electromagnetic radiation pulses obtained by triaxial fracture of granite samples
1
1998
... Rabinovitch等通过大量实验发现岩石产生的电磁辐射频率受裂纹宽度的限制,频率与裂纹宽度成反比,并给出了电磁辐射频率与裂纹宽度之间的关系[32 ] : ...
岩石破裂电磁辐射频率与岩石属性参数的关系
1
2009
... 根据波动理论以及瑞利波速公式[33 ] : ...
岩石破裂电磁辐射频率与岩石属性参数的关系
1
2009
... 根据波动理论以及瑞利波速公式[33 ] : ...