瞬变电磁感应式天线分布电容零相位测试方法与应用

doi:10.11720/wtyht.2021.1488

瞬变电磁感应式天线分布电容零相位测试方法与应用

席振铢^,¹, 木仁¹, 徐昱^,², 周胜¹^,³, 陈兴朋³

1.中南大学地球科学与信息物理学院,湖南长沙 410083

2.湖南省计量检测研究院,湖南长沙 410014

3.湖南五维地质科技有限公司,湖南长沙 410205

The principle and application of zero phase measurement of resonant frequency of transient electromagnetic induction antenna

XI Zhen-Zhu^,¹, MU Ren¹, XU Yu^,², ZHOU Sheng¹^,³, CHEN Xing-Peng³

1. School of Geosciences and Info-Physics,Central South University,Changsha 410083,China

2. Hunan Institute of Metrology and Test,Changsha 410014,China

3. Hunan Wuwei Geological Technology Co., Ltd., Changsha 410205,China

通讯作者: 徐昱(1975-),女,硕士,高级工程师,主要从事电磁学计量研究工作。Email:xuyu19952020@163.com

责任编辑: 沈效群

收稿日期: 2020-10-26 修回日期: 2020-01-5

基金资助:

2016年湖南省标准化专项经费“等值反磁通瞬变电磁法通用技术标准”. 2011709

Received: 2020-10-26 Revised: 2020-01-5

作者简介 About authors

席振铢(1966-),男,教授,主要从事金属矿产和工程地球物理勘探方法技术与装备研发工作。Email: xizhenzhu@163.com

摘要

瞬变电磁感应式接收天线处于临界阻尼状态时,主输出信号才是纯目标体的感应信号。这种临界阻尼状态与接收天线的电感、分布电容以及电阻等电参数有关,其中电阻、电感值可以通过频谱仪直接测量得出,但是分布电容无法直接获取。为了能够研制高性能接收天线,本文提出了一种精确计算接收天线分布电容的方法。首先,构建瞬变电磁感应式接收天线等效电路模型;然后,推导输出信号零相位的谐振频率计算公式;最后,通过测量天线的谐振频率,并计算分布电容。为了验证了此方法的可行性,采用标准电容与计算电容比对,并测试了不同类型瞬变电磁感应式天线,测试结果表明:用零相位法计算分布电容精度高,方便快捷,可用于设计和制作高性能瞬变电磁感应式传感器。

关键词： 瞬变电磁 ; 零相位 ; 谐振频率 ; 分布电容

Abstract

When the transient electromagnetic receiving antenna is in a critically damped state, the output signal is the pure target induction signal. This critical damping state is related to electrical parameters such as inductance, distributed capacitance, and resistance of the receiving antenna. The resistance and inductance values can be directly measured by a spectrum analyzer, but the distributed capacitance cannot be directly obtained. In order to develop a high-performance receiving antenna, this paper proposes a method to accurately calculate the distributed capacitance of the receiving antenna. First, the equivalent circuit model of the transient electromagnetic induction receiving antenna is constructed; then, the calculation formula of the zero-phase resonance frequency of the output signal is derived; Finally, by measuring the resonant frequency of the antenna, the distributed capacitance is calculated. For the purpose of verifying the feasibility of this method, the standard capacitance is compared with the calculated capacitance, and different types of transient electromagnetic induction antennas are tested. The test results show that the zero-phase method can be used to calculate the distributed capacitance with high accuracy, convenience and fastness and can be used to design and produce high-performance transient inductive sensors.

Keywords： transient electromagnetic ; zero phase ; resonant frequency ; distributed capacitance

PDF (1337KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

席振铢, 木仁, 徐昱, 周胜, 陈兴朋. 瞬变电磁感应式天线分布电容零相位测试方法与应用. 物探与化探[J], 2021, 45(3): 737-741 doi:10.11720/wtyht.2021.1488

XI Zhen-Zhu, MU Ren, XU Yu, ZHOU Sheng, CHEN Xing-Peng. The principle and application of zero phase measurement of resonant frequency of transient electromagnetic induction antenna. Geophysical and Geochemical Exploration[J], 2021, 45(3): 737-741 doi:10.11720/wtyht.2021.1488

0 引言

瞬变电磁法^[1,2](TEM)又称时间域电磁法,通过直接观测二次场,达到探测地下地质体的目的。由于受地形影响小、施工效率高,广泛应用于矿产、煤田以及水文等地质勘探中,近几年已逐渐向大深度矿产^[3]和油气资源勘探^[4,5]方向发展。在瞬变电磁法中,当接收天线处于临界阻尼状态时^[6,7],输出信号接近感应信号。此时不仅响应速度快,且不会出现振荡,是阶跃响应的最佳状态^[8,9]。通过改变天线的电参数可以使电路接近临界阻尼状态,其中电阻、电感可以直接测量得出,但是分布电容无法直接测量得到,只能使用间接的方法进行测量^[10,11]。此分布电容与传统意义上的双极板电容是不同的,当电流通过不是理想导体的线圈时,在导线间产生电势差,导线周围区域出现电场,将这些以电场形式储存的能量等效成分布电容,主要与线圈绝缘层介电常数和厚度、线圈匝间距等参数有关^[12]。

到目前为止,计算线圈分布电容的方法有建模法、有限元法、解析法等。有限元法^[13]是根据线圈的静电储能与线圈两端的电压推导出线圈的分布电容,这种方法计算结果比较精确,但存在计算数据庞大、求解过程十分复杂,且针对不同的线圈只能单独计算,没有固定的公式进行求解等问题。建模法^[14,15]是通过实验测出一些集总参数,据此建立相关模型再推导出线圈的分布电容,这种方法受模型限制较大,测出的参数精度也存在较大误差,导致大部分的测试结果差强人意。解析法^[16]是测量线圈的物理和几何参数,再以这些参数之间的几何关系推导出分布电容,目前常用的解析法有阻抗等效法和谐振法。等效阻抗法是利用测量阻抗与等效电路阻抗相等原理来计算分布电容,通过LCR表串联模式测得线圈的电感值得出测量模型电路阻抗,根据线圈分布电容和电感得到接收线圈等效电路阻抗,构建测量阻抗与接收线圈等效电路阻抗等式得到测量电感与线圈电感的关系式;在2个测试频率下使用LCR表测得2个测量电感值,根据谐振频率计算公式得到线圈的分布电容。谐振法则是在线圈两端串联一个阻值等于线圈内阻的外加电阻,线圈两端再加入幅值不变、信号频率不断增大的激励源电压,测量外接电阻两端电压值,当电阻两端电压幅值为零(最小)时,外加的信号频率即为线圈的谐振频率。目前谐振法的使用最为广泛。

本文使用的零相位方法,是通过输出电压获得接收天线的谐振频率,当线圈的输出电压相位为零时,此时输出信号的频率就是接收天线的谐振频率,再根据公式计算分布电容。这种方法更加方便、准确,可以用于瞬变电磁感应天线的设计与制作的理论依据。

1 零相位测量方法原理

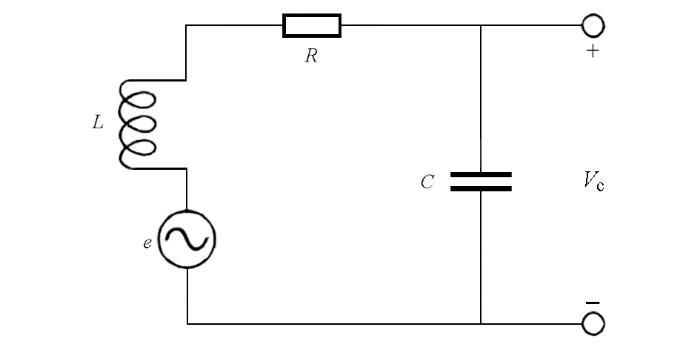
瞬变电磁感应式接收天线作为一种电感线圈,其内阻、自感和分布电容组成了一个振荡电路,其等效电路模型如图1所示,其中:R代表接收线圈的内阻,L代表自感,C代表分布电容,e代表信号源。感抗和容抗相等时,振荡电路呈全阻性,接收天线线圈的输出电压V_c的相位为零,此时对应的频率为接收天线的谐振频率,也是振荡电路的固有谐振频率,再根据谐振频率公式计算接收天线的分布电容。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 等效电路模型

Fig.1 Equivalent circuit model

由电路原理,可得线圈的输出电压V_c(jω)为:

(1)

V_{c} (j ω) = \frac{e (j ω)}{1 + j ωCR - ω^{2} LC}

式中:ω为角频率,

(2)

ω = 2 π f, e (j ω) = j ω μ_{0} nS,

(3)

V_{c} (j ω) = \frac{j ω μ_{0} nS}{1 + j ωCR - ω^{2} LC} 。

式中:f为频率,μ₀为真空磁导率,n为线圈匝数,S为线圈截面积。经过变换可得:

(4)

V_{c} (j ω) = \frac{j (1 - ω^{2} LC) ω μ_{0} nS + ω^{2} μ_{0} nSCR}{(1 - ω^{2} {LC)}^{2} + {(ωCR)}^{2}},

令:a= $\frac{ω^{2} μ_{0} nSCR}{(1 - ω^{2} {LC)}^{2} + {(ωCR)}^{2}}$ ,

b= $\frac{j (1 - ω^{2} LC) ω μ_{0} nS}{(1 - ω^{2} {LC)}^{2} + {(ωCR)}^{2}}$

则有: (5)V_c(jω)=a+bj 。

当发生谐振时,电路呈阻性: $1 - ω^{2} LC = 0;$ 谐振角频率为: $ω_{0} = \frac{1}{\sqrt[]{LC}} 。$ 此时,输出电压的幅值和相位分别为:

(6)

| V_{c} | = |\frac{μ_{0} nS}{CR}|,

(7)

φ = \arctan (\frac{b}{a}) = \arctan (0 / \frac{μ_{0} nS}{CR}) = 0 。

由式(7)可以看出,当输出电压V_c相位响应为零时,电路呈纯阻性,发生谐振,电路此时对应的频率即为谐振频率。

2 方法验证

为了验证零相位测量方法的可行性,构建接收天线的等效电路,使用零相位方法计算电容值。使用WK3260B精密磁性元件分析仪测量输出电压相位,此仪器基本量测精确度为0.1%,符合测量精度要求。当输出电压相位响应为零时获得电路的谐振频率,根据谐振频率公式换算得出的电容值记为计算值,再使用WK3260B精密磁性元件分析仪对电容进行直接测量,测量结果作为电容的实际值。实际工作中使用的瞬变电磁接收天线分布电容大多数为几十皮法(pF),所以选择单位量为pF的标准实验电容、电阻、电感元器件,电阻、电感元器件的实际数值也由WK3260B精密磁性元件分析仪测量得出。以电容为测试对象,电感、电阻值固定不变,选取6个规格不同的电容进行6组实验,各标准实验电子元件参数和实际值见表1。

表1 电子元件参数

Table 1 Parameters of electronic components

标准实验电子元件	标准参数	实际数值
电感L/mH	7.2×(1±0.05)	7.298
电阻R/Ω	500.0×(1±0.05)	512.0
电容C/pF	30.0×(1±0.1)	31.8
	100.0×(1±0.05)	99.0
	220.0×(1±0.05)	222.8
	330.0×(1±0.05)	328.2
	470.0×(1±0.05)	474.0
	680.0×(1±0.05)	689.6

新窗口打开| 下载CSV

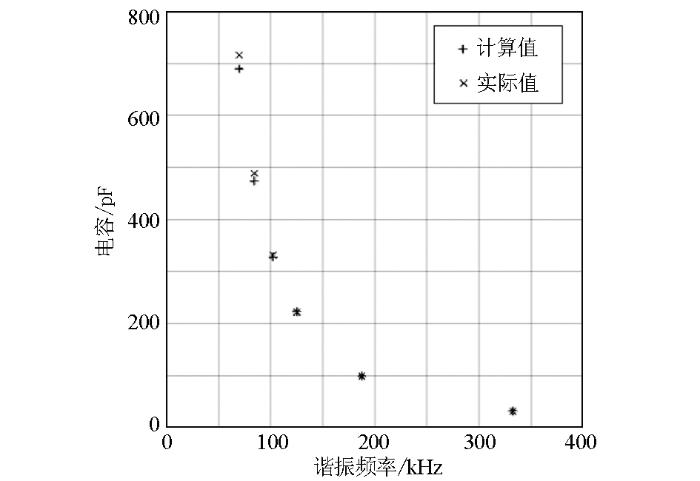
通过零相位谐振法测出此等效电路的谐振频率,电感已知,根据谐振频率公式计算出电容值,并与实际值对比,结果见表2。可以看出,通过零相位法计算的电容值与标准电容值基本相同,误差不超过5%。计算结果准确,证明了根据输出电压零相位计算分布电容的方法是可行的。

表2 电容的测试结果

Table 2 Capacitance measurement results

谐振频率/kHz	实际值/pF	零相位法计算值/pF	误差/%
332.410	31.8	31.44	1.1
187.579	99.0	98.74	0.3
125.142	222.8	221.86	0.4
102.397	328.2	331.36	1.0
84.346	474.0	488.36	3.0
69.680	689.6	715.58	3.8

新窗口打开| 下载CSV

3 测试方法应用

在验证此方法可行性的基础上,根据零相位方法研制瞬变电磁接收天线,并测试其性能(图2)。本次测试使用湖南五维地质科技有限公司研制的HPTEM瞬变电磁感应式接收天线,此接收天线采用分段结构(分两段)绕制,将2个多匝小线圈分为2段串联安装在接收骨架上。使用WK3260B精密磁性元件分析仪对感应式接收天线进行相位测量,当输出电压相位为零时得到接收天线的谐振频率,计算分布电容,得出临界阻尼状态下需要的匹配电阻值。瞬变电磁感应式天线等效电路如图3所示,r代表接收线圈的内阻,L代表电感,C代表分布电容,R1、R2、R3等效为匹配电阻R_T。2个线圈及整体线圈电参数见表3。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 零相位法计算与标准电容值的对比

Fig.2 Comparison of calculation with zero phase method and standard capacitance value

图3

新窗口打开| 下载原图ZIP| 生成PPT

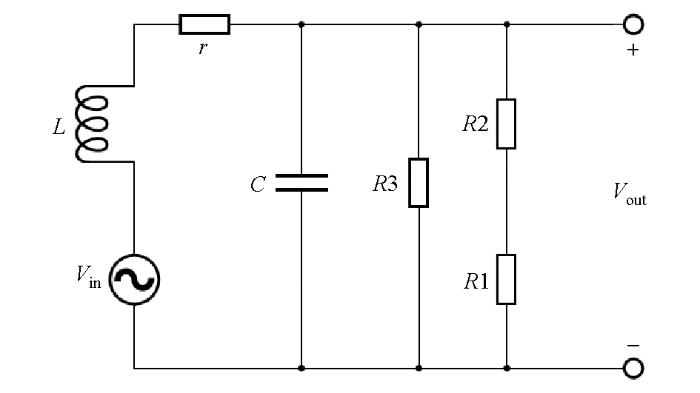
图3 瞬变电磁感应式天线等效电路

Fig.3 Transient electromagnetic induction antenna equivalent circuit

表3 线圈参数

Table 3 Coil parameters

	R/Ω	L/mH	f/kHz	C/pF
1号线圈	15.309	10.297	358.995	19.09
2号线圈	15.268	10.348	361.122	18.77
总线圈	30.634	29.140	223.335	17.43

新窗口打开| 下载CSV

匹配电阻:

(8)

R_{T} = \frac{R 3 (R 1 + R 2)}{R 1 + R 2 + R 3};

直流衰减系数:

(9)

α = \frac{R_{T}}{R_{T} + r};

阻尼系数:

(10)

K = \sqrt[]{α} (\frac{1}{2 R_{T}} \sqrt[]{\frac{L}{C}} + \frac{1}{2} r \sqrt[]{\frac{C}{L}}) 。

当阻尼系数K=1时,式(11)可等效变换为:

(11)

(4 - r^{2} \frac{C}{L}) R_{T}^{2} + 2 r R_{T} - \frac{L}{C} = 0,

(12)

R_{T} = \frac{L}{2 \sqrt[]{LC} - rC} 。

根据式(12)可以得出当阻尼系数为1时匹配电阻R_T的数值,它与接收天线自身的电参数有关。使用串并联的方式组合出适合的匹配电阻,令接收天线处于临界阻尼状态。表4给出了几组感应式天线不同阻尼系数下对应的电阻值。

表4 电阻参数

Table 4 Resistance parameters

阻尼系数K	电阻			R_T/kΩ
阻尼系数K	R1/kΩ	R2/kΩ	R3/kΩ	R_T/kΩ
0.080	560	560	470	331.069
0.209	270	270	120	98.182
0.437	75	75	68	46.789
1.000	x	x	y	20.453
1.097	30	30	27	18.621
24.629	3.900	3.900	0.910	0.815
50.819	1.100	1.100	0.470	0.387
97.799	0.510	0.510	0.240	0.194

新窗口打开| 下载CSV

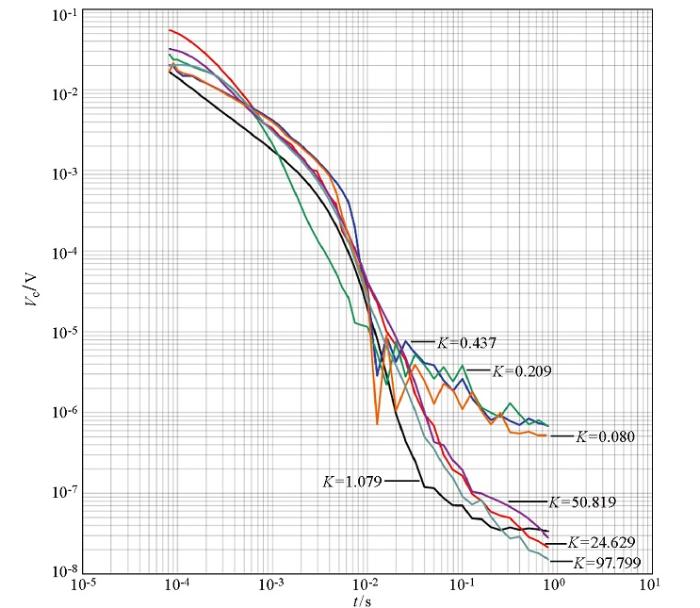
此次测试中,使用湖南五维地质科技有限公司同期研制的HPTEM主机、发送天线,与接收天线组成完整的瞬变电磁信号采集系统。根据表4,仅改变接收天线中电阻R1、R2、R3的数值,测试地点不变,信号发送频率为1 Hz,使用配套的HPTEM采集软件进行数据采集,绘制不同阻尼系数下接收信号的变化。由图4可以看出,当K=1时,线圈处于临界阻尼状态,信号响应速度快且不发生震荡,无过冲现象;当K>1时,线圈处于过阻尼状态,信号衰减速度慢,从最大值衰减到最小值有很长的过渡时间,随着K越来越大,响应速度越来越慢;当K<1时,线圈处于欠阻尼状态,信号出现振荡,衰减过程发生了畸变,随着K越来越小,失真现象越来越严重,振荡越来越大。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同阻尼系数接收信号对比

Fig.4 Comparison of received signals with different damping coefficients

根据零相位法得到此瞬变电磁感应式天线的分布电容,计算出阻尼系数为1时所需的匹配电阻,再选择合适的电阻以串并联的方式使接收天线达到最优状态。由图4可得,当R1=R2=30 kΩ、R3=27 kΩ时,K=1.097。感应式天线采集的信号平滑无振荡,过渡时间短,符合野外工作条件,可以应用于实际勘探任务。

4 结论

通过构建等效电路,应用振荡电路谐振时,输出信号相位为零的技术思路,测试获得谐振频率,根据谐振频率与分布电容的函数关系,计算感应天线分布电容。通过标准电容的检测和实际绕制的接收天线进行测试,得出如下结论:①零相位法计算感应天线分布电容,计算精度高,测试方法简便可行;②零相位测试方法可用来检测感应天线的性能;③零相位测试方法可作为高性能感应天线设计和制造的理论依据。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Nabighian M

, Macnae J

Time domain electromagnetic prospecting methods

[C]// Electromagnetic Methods in Applied Geophysics, 1991:427-520.