三维磁场有限元—无限元耦合数值模拟

doi:10.11720/wtyht.2021.1539

三维磁场有限元—无限元耦合数值模拟

郭楚枫^,, 张世晖^,, 刘天佑

中国地质大学(武汉) 地球物理与空间信息学院,湖北武汉 430074

3D magnetic field forward modeling by finite-infinite element coupling method

GUO Chu-Feng^,, ZHANG Shi-Hui^,, LIU Tian-You

Institute of Geophysics and Geomatics, China University of Geosciences(Wuhan), Wuhan 430074,China

通讯作者: 张世晖(1974-),男,博士,副教授,中国地质大学(武汉)毕业,研究方向为地质地球物理建模与反演。Email:zsh2008@cug.edu.cn

责任编辑: 王萌

收稿日期: 2020-12-1 修回日期: 2021-01-13

基金资助:

雄安新区深层地热资源探测评价技术示范项目. 2018YFC0604303
深部资源预测系统技术研究与示范项目. 2017YFC0601504

Received: 2020-12-1 Revised: 2021-01-13

作者简介 About authors

郭楚枫(1996-),男,在读硕士研究生,研究方向为重磁勘探。Email: gcf2013@cug.edu.cn

摘要

利用传统有限单元法在有限空间范围内开展三维地球物理场正演模拟时,由于截断边界的影响,会引起局部异常的畸变,影响数值模拟的精度,对该问题通常采用扩边的办法加以解决,但需要的范围较大,从而大大增加运算成本,影响正演模拟效率。本文基于COMSOL Multiphysics软件,在求解域外部边界设置无限元以替代传统边界条件,达到减小计算区域目的。通过孤立球体和组合模型磁场正演模拟,考虑退磁、剩磁及地表起伏条件,与传统有限元方法相比,有限元—无限元耦合算法能够有效克服边界效应,提高计算精度,降低运算量,从而提高了有限单元法正演数值模拟效率。

关键词： 有限元—无限元 ; 三维正演 ; 磁法勘探 ; COMSOL

Abstract

Due to the influence of the artificial boundary condition, when the conventional finite element method is used to carry out the forward simulation of the three-dimensional geophysical field in a limited space, local abnormal distortion may occur, which affects the accuracy of the numerical simulation. This problem is usually solved by expanding the edge, but this requires a larger range, which greatly increases the computational cost and affects the efficiency of forward simulation. In this paper, on the basis of COMSOL Multiphysics software, infinite elements are set on the external boundary to replace the traditional boundary conditions so as to reduce the calculation area. Compared with the traditional finite element method, the finite element infinite element coupling method, by setting the isolated sphere and the combined body model and considering the conditions of demagnetization, remanence and surface undulation, can effectively overcome the boundary effect, improve the calculation accuracy and reduce the amount of calculation, thus improving the forward numerical simulation efficiency of the finite element method.

Keywords： finite-infinite ; 3D forward modeling ; magnetic prospecting ; COMSOL

PDF (7208KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郭楚枫, 张世晖, 刘天佑. 三维磁场有限元—无限元耦合数值模拟. 物探与化探[J], 2021, 45(3): 726-736 doi:10.11720/wtyht.2021.1539

GUO Chu-Feng, ZHANG Shi-Hui, LIU Tian-You. 3D magnetic field forward modeling by finite-infinite element coupling method. Geophysical and Geochemical Exploration[J], 2021, 45(3): 726-736 doi:10.11720/wtyht.2021.1539

0 引言

有限单元法是地球物理数值正演模拟方法的一种,以变分问题为基础,根据地球物理中的偏微分方程和边界条件,用数值方法近似计算地球物理场值,适用于复杂物性分布和复杂边界形状的地球物理计算^[1]。自1971年Coggon首次系统地阐述了有限单元法在电、电磁法中的应用以来^[2],有限单元法已经广泛应用于复杂形态、复杂地质条件的地球物理正演中。

在电磁法领域,基于非结构化网格的矢量有限单元法,具有很强的适应性,是目前国内外研究的热点^[3,4,5]。随着研究的深入,各向同性假设模型已难以满足解释的需要,基于有限元的各向异性研究受到了广泛关注^[6,7,8]。在重力勘探中,有限单元法常用来进行梯度张量及重力矢量的正演模拟计算^[9,10,11,12],Cai和Wang^[11]实现了利用有限元法计算非均匀复杂形体重力异常的快速算法,朱自强等^[13]则利用有限单元法进行重力异常的地形校正。在磁场正演模拟中,有限单元法的优势在于不需要引入均匀磁化设定,能同时考虑磁各向异性、退磁效应、剩磁三种因素的影响^[14],所以在充分考虑退磁作用、进行高精度磁测资料反演解释时,常用有限单元法进行正演模拟^[15,16]。

上述的有限元计算存在相同的问题,即采用传统截断边界,在一个相对较大的区域内,将无穷的边界问题近似为有限区域进行^[17]。而有限单元法是一种区域型方法,必须在全区域进行剖分,对于地球物理正演中的无界区域问题,在边界处产生畸变会影响对异常的解释。一般的解决方法是进行扩边,即设定更大的求解区域以减小传统截断边界的影响。如蒋甫玉等^[9]进行三度体重力矢量有限元正演计算时提出,设置求解域边界长度应大于场源体长度的7.5倍以达到理想效果;Ren和Kalscheuer等^[5]进行三维有限元大地电磁正演时,设置了边长为20 km的求解域,以保证长度100 m的板状体模型正演能达到模拟精度。扩边往往造成有限元计算区域大,节点数多,进一步降低了有限元正演的计算效率^[17],较合理的策略是将计算区域限定在较小的目标区域范围内,减少单元与节点数量,以节约计算资源,提高正演效率。利用无限单元取代传统的边界条件,通过坐标映射将“无限单元”沿某一方向无限扩展,最后结合有限单元法对内部区域进行正演模拟,提高正演效率。

无限元的概念最早由Ungless在1973年给出,并实现了衰减型无限单元^[18]。无限元大体可以分为3类:Bettess映射无限元^[19,20]、Astley波包映射无限元^[21,22](mapped wave envelope elements)和Burnett多级展开无限元^[23,24],其中Astley波包映射无限元应用最广。无限元的基本思路是通过坐标变换,采用和位场不同的插值函数,通过坐标映射实现无限域积分,并在映射后的局部坐标里建立位场插值形函数,使位场在有限元网格和无限元网格结合处保持一致性,而在无限远处衰减为0^[25]。目前,无限元广泛应用于声学、岩土力学等方面^[26,27],在地球物理学中则主要应用于地震、测井和电法领域:Fu和Wu^[28]应用无限元处理了弹性波的吸收边界条件;朱军等^[29]则利用无限元模拟测井中面临的无穷边界问题;汤井田等^[30]应用无限元进行了三维直流电阻率的数值模拟;张林成等^[17]应用无限元进行了基于二次场的可控源电磁法的三维数值模拟。目前,混合有限元—无限元在磁场正演模拟中应用较少。为提高有限元三维磁场正演模拟的效率,本文基于COMSOL Multiphysics软件,在求解域外部边界上设置无限元,综合考虑剩磁、退磁及地表起伏,通过一系列的数值模拟,与解析算法和传统有限元方法进行对比,一方面验证了方法的有效性,另一方面证明本算法在保证精度的同时能够大大提高正演效率。

1 方法理论

1.1 有限单元法原理

对于地球物理中磁场的正演问题,其边界条件是依据麦克斯韦方程组给出的:

(1)$\nabla \times {H}={J}+\frac{\partial {D}}{\partial t} ① \\ \nabla \times {E}=-\frac{\partial {B}}{\partial t} ② \\ \nabla \cdot {B}=0 ③\\ \nabla \cdot D=\rho ④$

式中:H为磁场强度,B为磁感应强度,J为传导电流密度,D为电位移,E为电场强度,t为时间,ρ为空间某点处自由电荷体密度。实际磁法勘探中,只考虑地磁场对目标体的影响,即在正演中认为地质体处于无电流源的静磁场环境中。由麦克斯韦方程组①式,当空间中的位移电流密度 $\frac{\partial D}{\partial t}$ 和传导电流密度J均为0时,有

$\nabla \times {H}=0,$

即在无电流源的磁场空间中磁场强度H和磁感应强度B,应该满足:

$\nabla \times {H}=0, \nabla \cdot {B}=0。$

H和B的关系为:

$B = μ_{0} (H + M),$

其中:μ₀为真空中的磁导率,M为磁化强度,由感应磁化强度M_i和剩余磁化强度M_r组成

$M = M_{i} + M_{r},$

而感应磁化强度M_i与磁场强度H成正比

$M_{i} = χH,$

其中:χ为磁化率,由以上关系式可以推出

(2)$\begin{aligned} \nabla \cdot {B} &=\nabla \cdot \mu_{0}\left[(1+\chi) {H}+{M}_{r}\right] \\ &=\nabla \cdot \mu_{0}\left(\mu_{r} {H}+{M}_{r}\right)=0, \end{aligned}$

式中:μ_r=(1+χ)为相对磁导率。由$\nabla$×H=0,可以引入磁标位V_m:

${H} =-\nabla V_{m},$

带入式(2)中,得

(3)$\nabla \cdot\left(\mu_{r} \nabla V_{m}-{M}_{r}\right)=0。$

这是包括感磁和剩磁的磁标位基本方程。

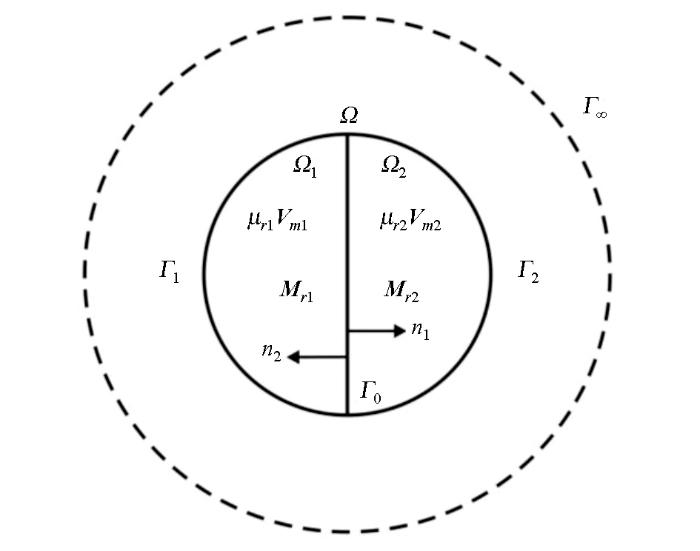
图1为磁场正演中非均匀介质分布的简单模型,Γ₀为两介质共有边界,Γ₁、Γ₂为两介质的外部边界,Γ_∞为区域外部边界,V_m₁、V_m₂、μ_r₁、μ_r₂、M_r₁、M_r₂分别代表界面两侧介质中的磁位、相对磁导率和剩余磁化强度。徐世浙^[1]已经证明,磁位边值问题中的内部边界条件属于自然边界条件,使用有限单元法解偏微分方程(3)时,无需讨论磁位的内部边界条件。因此有限单元法具有解决非均匀介质的磁场正演能力。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 非均匀介质分布(改自徐世浙,1994)

Fig.1 Distribution of inhomogeneous medium (modified from Xu Shizhe,1994)

给定V_m的外边界条件,将计算区域Ω取足够大,使得区域的边界Γ_∞与磁性体足够远,这时磁性体引起的磁位在边界上近似为零。但在磁法勘探中存在着正常地磁场T,Γ_∞上的磁位是由T决定的,所以Γ_∞上有第一类边界条件:

(4)

V_{m} = - T \cdot r, \in Γ_{\infty};

式中:r是坐标原点至边界点的矢径。转为第二类边界条件

(5)

\frac{\partial V_{m}}{\partial n} = - T_{n}, \in Γ_{\infty} 。

针对基本方程(3)及边界条件(5),可以构造泛函

(6)$I\left(V_{m}\right)=\int_{\Omega}\left[\frac{1}{2} \mu_{r}\left(\nabla V_{m}\right)^{2}-\nabla V_{m} \cdot {M}_{r}\right] \mathrm{d} \Omega,$

由于内部边界条件为自然边界条件,考虑Γ_∞的边界条件式(5),以及自由空间中μ_r=1,M_r=0,式(6)的变分为

$\begin{array}{l} δ I (V_{m}) = \int_{Γ_{\infty}} (μ_{r} \frac{\partial V_{m}}{\partial n} - M_{r, n}) δ V_{m} d Γ = \\ - \int_{Γ_{\infty}} T_{n} δ V_{m} d Γ = - δ \int_{Γ_{\infty}} T_{n} V_{m} d Γ 。 \end{array}$

因此,无电流静磁场的磁位的边值问题与下列的变分问题相应:

(7)$F\left(V_{m}\right)=\int_{\Omega}\left[\frac{1}{2} \mu_{r}\left(\nabla V_{m}\right)^{2}-\nabla V_{m} \cdot {M}_{r}\right] \mathrm{d} \Omega+\\ \int_{\Gamma_{\infty}} {T}_{n} V_{m} \mathrm{~d} \Gamma,\\ \delta F\left(V_{m}\right)=0$

1.2 有限元—无限元耦合算法

有限元—无限元耦合算法将整个求解区域分为有限元区域和无限元区域,用无限元区域代替传统的外边界,在两个区域分别采取有限元分析和无限元分析,通过总体刚度矩阵组装将两者结合起来从而进行数值求解。

图2a中划分了有限元和无限元计算区域,图中有限元区域为目标区域,包含场源、目标体及测点等;无限元区域为有限元区域边界至无穷远,为边界计算区域。无限元分析就是在该区域的某一方向上,采用无限元映射和形函数,将整体坐标映射到局部坐标上来,其原理与有限元分析相同。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 三维无限元映射(改自汤井田等,2010)

Fig.2 3-D infinite element mapping(modified from Tang et al.,2010)

使用有限单元法计算时,采用四面体单元网格剖分,线性插值单元中的插值函数为:

(8)

V_{m} = \overset{4}{\sum_{i = 1}} N_{i} V_{mi},

式中:N_i为插值形函数,与四面体自然坐标形同;V_mi为节点上的磁标位值。

无限元单元分析时,采用六节点,图2a给出了三维无限元映射示意,图中节点1、2、3、4、5、6为无限元基本要素,P点为坐标原点,节点1、2、3为有限元边界上某单元的三节点,P点到节点4、5、6的距离分别为P点到节点1、2、3距离的两倍。无限单元最外围的3个节点为无穷远。无限元分析就是通过无限元映射将无穷坐标映射到图中的局部坐标上。

图2b中ζ方向表示无限元映射的方向,在ξ-η平面内,无限单元与有限单元采用相同的映射形式和形函数。无限元的坐标映射为

$x = \overset{3}{\sum_{i = 1}} L_{i} x_{i}, y = \overset{3}{\sum_{i = 1}} L_{i} y_{i} 。$

式中:L_i为三角形面积坐标。结合图2有:

(9)

\{\begin{array}{l} L_{1} = ξ, \\ L_{2} = η, \\ L_{3} = 1 - ξ - η 。 \end{array}

结合ζ方向的坐标映射关系式,可以得到六节点无限单元的结点坐标映射函数:

(10)

x = \overset{6}{\sum_{i = 1}} N_{i} x_{i}, y = \overset{6}{\sum_{i = 1}} N_{i} y_{i}, z = \overset{6}{\sum_{i = 1}} N_{i} z_{i} 。

其中:

$N_{i} = L_{i} \frac{- 2 ζ}{1 - ζ}, N_{i + 3} = L_{i} \frac{1 + ζ}{1 - ζ}, i = 1,2, 3 。$

经过上述映射之后,磁位借助无限单元延伸至无限远处,并且在无限远处衰减为零。对于无限元形函数,其具体的表达式如下:

(11)

\begin{array}{l} M_{i} = L_{i} \frac{1 - ζ}{2} \frac{- (1 - ζ)}{2} ζ, \\ M_{i + 3} = L_{i} \frac{1 - ζ}{2} (1 - ζ^{2}), \\ i = 1,2, 3 。 \end{array}

该形函数是Astley映射无限元理论^[21]中采用的形函数中的系数(1-ζ)/2与二阶Lagrange插值多项式的乘积。

对有限元—无限元进行单元分析后,对方程组进行总体合成,再解相应的大型线性方程组即可得到各个节点的磁位。得到各节点的磁位后,通过磁场强度与磁位的关系,求得磁场的各个分量:

(12)

\{\begin{array}{l} H_{ax} = - μ_{0} \frac{\partial V_{m}}{\partial x}, \\ H_{ay} = - μ_{0} \frac{\partial V_{m}}{\partial y}, \\ Z_{a} = - μ_{0} \frac{\partial V_{m}}{\partial z} 。 \end{array}

2 模型试算

为说明有限元—无限元算法的优势,综合考虑剩磁和退磁的影响,设计了两种模型:球体模型和组合体模型。使用COMSOL Multiphysics软件进行建模,以下数值模拟平台均为Intel(R) Xeon(R) CPU3.91G,64GB RAM,16CPUs。

2.1 球体模型

在磁场正演模拟中,忽略退磁和剩磁会对正演结果产生较大的影响,忽略剩磁的相对误差与Q(科尼斯布格比)相关,而忽略退磁的相对误差与磁化率相关,若Q=0.5,忽略剩磁的相对误差可达到33%以上^[31]。相比于一般的正演方法,有限单元法的优势在于适用于复杂条件、复杂形状的地球物理计算。为突出有限单元法的优势,验证基于有限元—无限元耦合的磁场正演算法的准确性,设计了如图3所示的模型。由于球体的退磁系数为常数,可以利用退磁改正公式计算磁异常,将传统有限元方法,有限元—无限元耦合方法和解析解进行对比。

图3

新窗口打开| 下载原图ZIP| 生成PPT

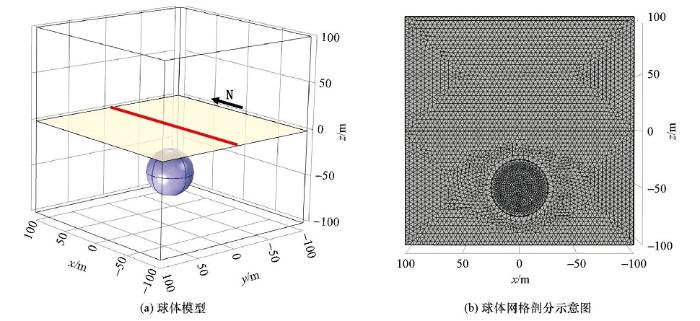
图3 球体模型及网格剖分示意(蓝色为球体模型,红色直线代表测线,黄色为观测平面范围)

Fig.3 Diagram of the Sphere model and mesh generation(the blue region is the sphere, the red line is observation line, the yellow plane is the range of observation plane)

图3a所示的模型求解域边界长度为200 m,图3b为模型的网格剖分情况,区域网格节点数为 383 250。地磁场参数及球体参数为:地磁场大小T₀=50 000 nT,地磁倾角I₀=60°,偏角A₀=0°。球体模型中心埋深50 m,半径为25.07 m,剩余磁化强度为常量,大小为19.89 A/m,剩磁倾角I_r=50°,偏角A_r=60°,球体模型磁化率k=6 SI。观测平面在z=0平面,为200 m×200 m的方形区域,x和y的坐标范围均为-100~100 m。测线位于观测平面上,测点分布在x=-100~100 m,y=0的直线上。由于球体模型Q=0.083,需要进行退磁改正以确保正演的准确性。球体的退磁系数N=1/3为常数,在地磁场H₀的作用下,使用退磁改正公式:M= $\frac{1}{1 + Nk}$ (kH₀+M_r)进行计算。

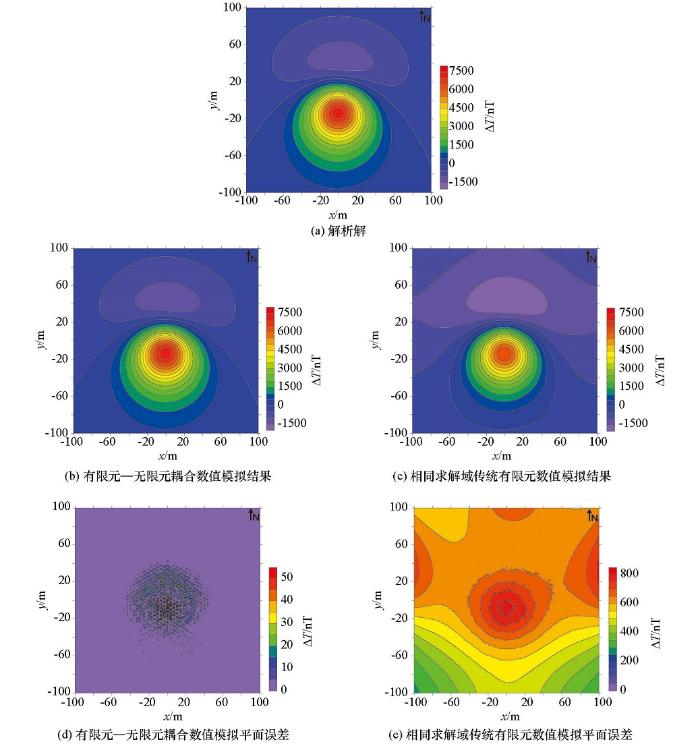
在相同的求解域设置和相同网格剖分条件下,分别使用有限元—无限元耦合算法和传统有限元方法进行数值模拟。图4a为经过退磁改正后的球体ΔT磁异常特征图,图4b为有限元—无限元耦合算法的数值模拟结果,图4c为传统有限单元法数值模拟结果。图4d、图4e为平面误差分布。图4b中基于有限元—无限元耦合算法的结果与图4a中解析解的异常形态特征及幅值基本一致,图4d中,有限元—无限元耦合算法在边界处几乎没有产生误差。传统有限元数值模拟结果与解析解差别较大,图4c和图4e中,求解域边长为200 m的传统有限元数值模拟得到的ΔT磁异常幅值与解析解相比,最大偏差达到837 nT,而在边界处异常形态差别较大。此例说明,传统有限单元法进行数值模拟时在边界处会产生较大的误差,严重影响了正演模拟的精度。而在相同的计算范围内,基于有限元—无限元耦合的算法的数值模拟结果非常优秀,特别在边界附近达到了很高的精度,明显优于传统有限元算法的结果。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同方法正演的球体平面ΔT磁异常及其平面误差分布

Fig.4 The plane total-field anomaly of the sphere using different methods

扩大求解域的范围,利用传统有限单元法进行数值模拟,再与有限元—无限元耦合算法进行对比。

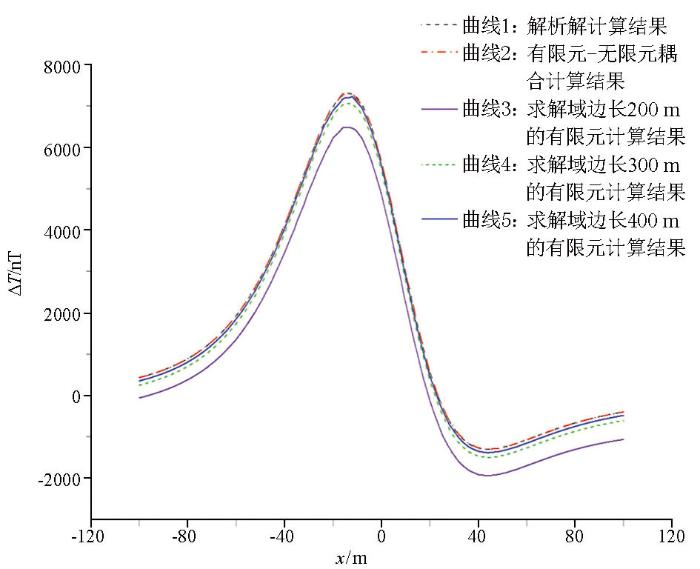
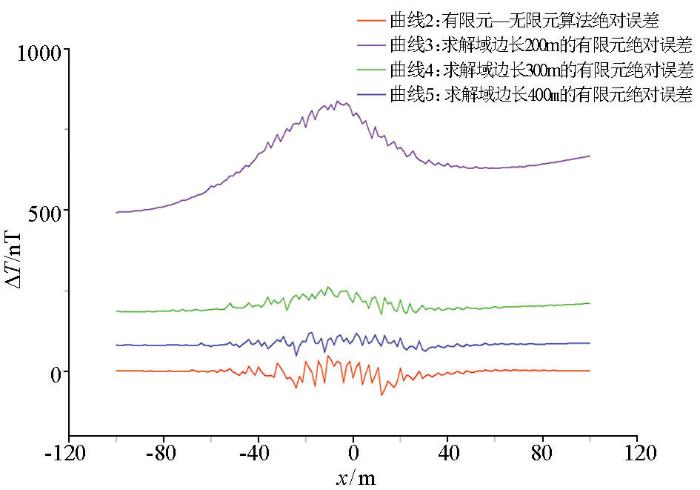
求解域一的长宽高分别为300、300、300 m,求解域二为400、400、400 m。图5为相同磁场参数的球体模型,在相同网格剖分条件下,使用不同方法计算得到的ΔT磁异常曲线。曲线1为解析解,曲线2为基于有限元—无限元的计算结果,曲线3为求解域边界长度为200 m的传统有限元计算结果,曲线4为求解域边界长度为300 m的传统有限元计算结果,曲线5为求解域边界长度为400 m的传统有限元计算结果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同方法正演的球体磁异常曲线

Fig.5 The total-field anomaly curve of the sphere using different methods

在进行三维有限元数值模拟时,由于受到6个方向的截断边界影响,使用传统有限单元法进行三维正演时,若要提高精度,需要在空间的6个方向对模型进行延展。图5和图6中,对比解析解(曲线1)和传统有限元(曲线3、曲线4和曲线5)的结果,随着求解区域的逐渐增大,传统有限单元法在观测平面边界处产生的误差逐渐减小,正演精度也在逐渐提高。当求解域边界长度达到400 m时,即对应曲线5的结果,传统有限元的数值模拟结果和解析计算结果已经十分接近,但是仍然存在约85 nT的平均绝对误差,且随着求解区域的扩大,传统有限单元法的精度增加有限,图5中曲线5和曲线1也不重合。图5中,解析解对应的曲线1和有限元—无限元数值模拟对应的曲线2几乎完全重合,基于有限元—无限元算法所产生的绝对误差在0左右,说明了基于有限元—无限元算法的准确性。对比有限元—无限元(曲线2)和求解域边长为200 m的传统有限元(曲线3)的数值模拟结果,在相同的区域内,基于有限元—无限元的算法(曲线2),在边界处所产生的绝对误差基本为0,基本避免了截断误差,大大改善了边界处的计算结果,再次说明基于有限元—无限元算法相对于传统有限元算法,在边界处能够得到更高的精度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 绝对误差分布曲线

Fig.6 The absolute error distribution curve

不同有限元算法模型的计算效率和误差对比如表1所示。基于有限元—无限元的算法需要对外部设置的无限元区域进行网格剖分,所以相对初始模型会生成更多的网格节点。由表1可知,当求解域边界长度设置为400 m时,传统有限元算法的平均相对误差为8.4%,均方根误差为86.1 nT,最大绝对误差为120.9 nT,相对于初始模型的计算精度有了很大的提升。但是其设置边界长度过大,求解区域的大小增大了近12倍,计算所需要的时间为240 s,占用了超过20 GB的内存,若观测平面范围增大,在保证精度的情况下,求解域会进一步增大,计算量也会进一步增加,严重影响了有限元数值模拟的正演效率,大大增加了运算成本。而基于有限元—无限元算法的平均相对误差仅有0.78%,是使用扩边算法精度的10倍,占用内存为4.85 GB,仅为扩边算法的 1/5,而运算时间则提高了2.4倍。所以,综合考虑剩磁和退磁的球体模型实验结果说明:基于有限元—无限元的算法,在相同的计算区域时,边界处能够达到更高的精度;同时也说明在相同的精度下,基于有限元—无限元算法与传统有限元算法相比能够在相对更小的区域内达到精度要求,使用的节点数更少,占用内存更少,大大降低了运算成本,提高了正演模拟的精度。

表1 不同算法模型计算效率及误差对比

Table 1 Comparison about efficiency and relative error of different model

方法	有限元求解域边长 /m	网格节点数	平均网格间距 /m	占用内存 /GB	计算时间 /s	最大绝对误差 /nT	均方根误差 /nT	平均相对误差 /%
有限元—无限元	200	453751	1.5	4.85	70	73.83	17.49	0.78
传统有限元	200	383250	1.5	4.33	34	837.88	656.69	63.90
传统有限元	300	1255245	1.5	12.06	120	261.82	205.02	20.27
传统有限元	400	2951989	1.5	23.91	240	120.91	86.13	8.41

新窗口打开| 下载CSV

2.2 组合体模型

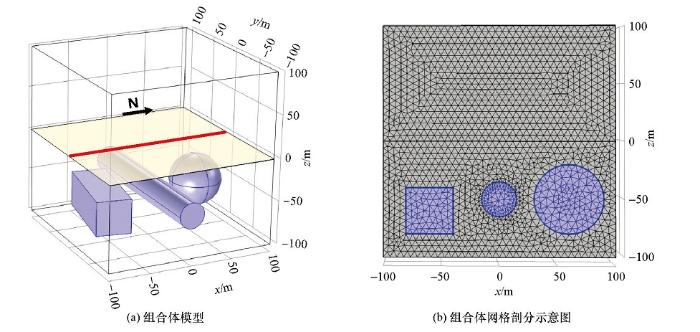
图7为多个地质体赋存的较复杂组合体模型,地磁场大小T₀=50 000 nT,地磁倾角I₀=45°,偏角A₀=0°;球体中心坐标为(60,0,-50),半径为30 m,剩余磁化强度大小为3.98 A/m,剩磁倾角I_r₁=50°,偏角A_r₁=60°,球体模型磁化率k₁=0.4 SI;圆柱体沿y方向无限延伸,埋深为50 m,截面半径为15 m,剩余磁化强度大小为7.96 A/m,剩磁倾角I_r₂=70°,偏角A_r₂=50°,磁化率k₂=0.5 SI;棱柱体中心坐标为(-60,0,-60),长100 m,宽40 m,高40 m,方位为西偏北10°,磁化率k₃=0.1 SI,剩余磁化强度为0。球体的退磁系数N₁=1/3,而对于任意横截面形状的无限长柱体,当与长度垂直方向磁化时,退磁系数N₂=1/2^[32],对球体和无限延伸圆柱体进行退磁改正,棱柱体磁化率较小且没有剩磁,则不进行退磁改正。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 组合形体模型及网格剖分示意(红色直线代表测线,黄色为观测平面范围)

Fig.7 Diagram of combined model and mesh generation(the red line is observation line, the yellow plane is the range of observation plane)

图7所示,模型求解域边界长度为200 m,观测平面设置在z=0平面,为200 m×200 m的方形区域,x和y的坐标范围均为-100~100 m。测线位于观测平面上,测点分布在y=-100~100 m,x=0的直线上。在相同的网格剖分情况下,分别使用基于有限元—无限元的算法和传统有限单元法进行计算。不同有限元算法数值模拟结果及平面误差分布如图8所示,计算效率和测线中的误差对比如表2所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

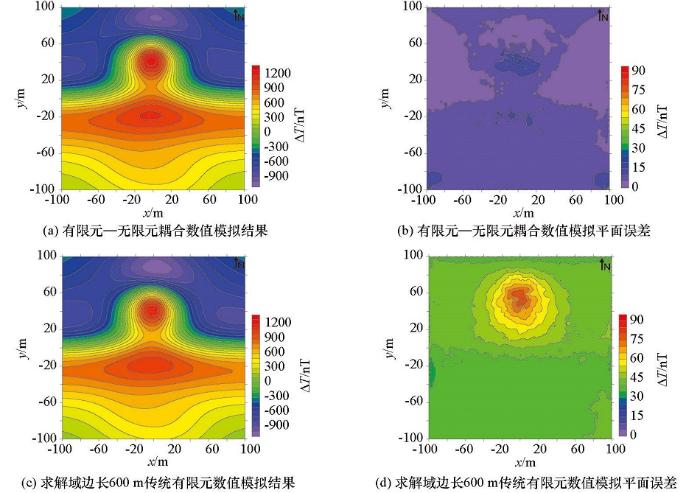
图8 有限元数值模拟结果及平面误差分布

Fig.8 The map of the Finite element numerical simulation results and plane error distribution

表2 组合形体计算效率及误差对比

Table 2 Comparison about efficiency and relative error of different model

方法	有限元求解域边长/m	网格节点数	平均网格间距/m	占用内存 /GB	计算时间 /s	最大绝对误差/nT	均方根误差/nT	平均相对误差/%
有限元—无限元	200	134853	5	3.67	109	35.22	12.53	1.68
传统有限元	200	114193	5	3.46	27	704.77	504.73	262.94
传统有限元	400	880751	5	10.98	60	159.25	114.61	18.02
传统有限元	600	2951638	5	28.46	262	98.21	50.32	7.62

新窗口打开| 下载CSV

图8中,两种有限单元法的数值模拟结果都能较好地展示z=0平面的ΔT磁异常形态特征,但是数值模拟的结果有较大的差异。传统三维有限元数值模拟共受到6个方向截断边界的影响,当求解域边界长度为600 m时,即求解域边界长度为观测区域边长的3倍,相对于初始模型求解范围增大了26倍,使平均相对误差降低到7.62%,但是其内存占用增加了近7倍,计算耗时增加了近9倍,图8d中,在z=0平面上仍存在近60 nT的绝对误差,说明传统算法提升计算精度能力差。而基于有限元—无限元算法,在边界处的误差为10 nT左右,平均相对误差为1.68%,占用内存仅为3.67 G。表明基于有限元—无限元算法能在占用更少运算资源的情况下,达到远高于传统有限单元法的计算精度,更适用于复杂模型体的三维磁场正演计算,进一步说明了基于有限元—无限元算法的优越性。

在组合体模型的基础上,将观测面设置为起伏地表,如图9所示,利用有限元—无限元方法进行正演数值模拟,网格剖分参数和表2中一致。

图9

新窗口打开| 下载原图ZIP| 生成PPT

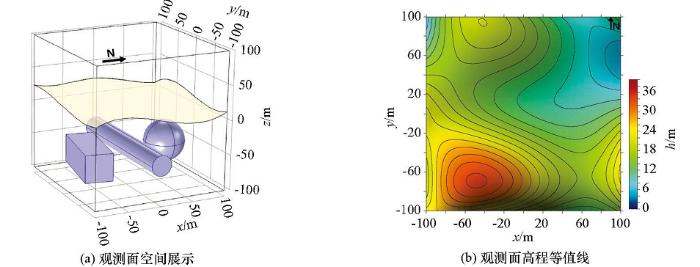
图9 起伏地表模型(黄色为观测面范围)

Fig.9 Diagram of rugged surface model (The yellow plane is the range of observation plane)

图10为模拟结果,图10b中有限元—无限元耦合算法的结果与图10a中的解析解的异常形态及幅值基本一致。数值模拟产生的最大绝对误差为49.87 nT,平均相对误差为3.04%,相对于观测面为z=0平面时误差有所增加,但仍处于较低的水平。说明基于有限元—无限元耦合算法适用于起伏地形情况,表明了有限元—无限元耦合算法的灵活性。

图10

新窗口打开| 下载原图ZIP| 生成PPT

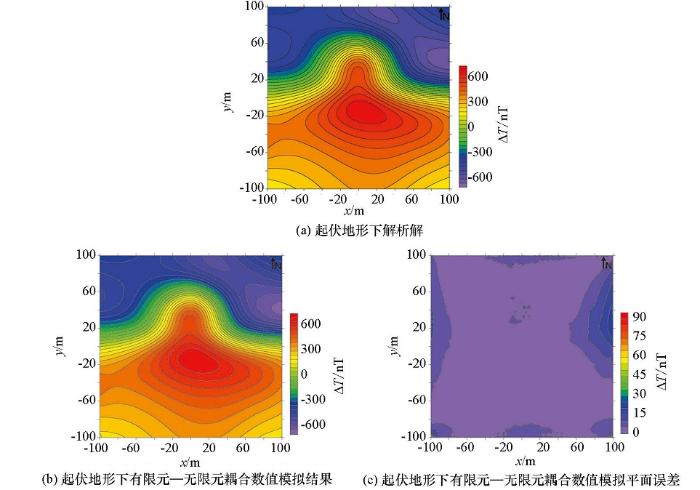
图10 起伏地形下有限元数值模拟结果及平面误差分布

Fig.10 The map of the Finite element numerical simulation results and plane error distribution in rugged surface

3 结论及讨论

1) 在进行磁场三维正演模拟时,有限单元法会受到6个方向的截断边界效应的影响,传统算法在扩大边界时会成倍的增加求解区域,占用大量运算资源,而计算精度的提升有限。在进行复杂条件下、复杂形体的正演模拟时,应该充分使用基于有限元—无限元的算法,以充分利用计算资源,提高正演效率。

2) 通过孤立球体模型和组合模型的数值模拟,在相同测区的计算范围内,有限元—无限元算法与传统的有限元算法相比,能够达到更高的计算精度。尤其是距离边界较近时,传统有限元方法误差较大,而在本文设置的模型中,基于有限元—无限元的算法能够达到2%以内的相对误差。

3) 传统的有限元方法为达到较高的精度,需要进行扩边处理,设置较大的求解区域范围,且随着求解域范围的扩大,精度提升有限。而基于有限元—无限元算法,只需与计算区域相当的网格剖分范围就可满足精度要求。相对于传统的有限元算法,有限元—无限元算法能在占用更少运算资源的情况下,达到远高于传统有限单元法的计算精度,正演效率更高。

4) 在起伏地形下,基于有限元—无限元耦合算法仍能高精度的完成数值模拟,进一步说明了有限元—无限元算法的灵活性,同时也表明该算法在复杂地质条件下有较好的应用前景。

致谢:

感谢中国地质大学(武汉)马火林副教授、朱丹博士后对本文提出的指导意见。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

徐世浙

. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.

[本文引用: 2]

Xu S

The finite element method in geophysics [M]. Beijing: Science Press, 1994.

[本文引用: 2]

[2]

Coggon J

Electromagnetic and electrical modeling by the finite element method

[J]. Geophysics, 1971, 36(1):132-132.

DOI:10.1190/1.1440151 URL [本文引用: 1]

[3]

赵宁, 王绪本, 余刚, 等.

面向目标自适应海洋可控源电磁三维矢量有限元正演

[J]. 地球物理学报, 2019, 62(2):779-788.