E-mail Alert Rss
 

物探与化探, 2021, 45(2): 473-479 doi: 10.11720/wtyht.2021.1307

方法研究·信息处理·仪器研制

理论模型分析卡尔曼滤波在航空全张量磁力梯度测量中的应用效果

孟庆奎,1,2, 周坚鑫1,2, 舒晴1,2, 高维2, 徐光晶2, 王晨阳2

1.自然资源部 航空地球物理与遥感地质重点实验室,北京 100083

2.中国自然资源航空物探遥感中心,北京 100083

Application effect of Kalman filter in airborne full tensor magnetic gradient measurement based on theoretical model

MENG Qing-Kui,1,2, ZHOU Jian-Xin1,2, SHU Qing1,2, GAO Wei2, XU Guang-Jing2, WANG Chen-Yang2

1. Key Laboratory of Airborne Geophysics and Remote Sensing Geology, Ministry of Natural Resources, Beijing 100083, China

2. China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China

责任编辑: 王萌

收稿日期: 2020-06-16   修回日期: 2020-10-7   网络出版日期: 2021-04-20

基金资助: 航空物探遥感中心青年创新基金.  2020YFL16
国家重点研发计划.  2017YFC0601601

Received: 2020-06-16   Revised: 2020-10-7   Online: 2021-04-20

作者简介 About authors

孟庆奎(1987-),男,硕士,工程师,主要从事应用地球物理方法研究和数据处理解释工作。Email: qingkui_meng@163.com

摘要

航空全张量磁力梯度测量数据中包含非常复杂的运动噪声,在频谱图中从低频至高频均有分布,并以白噪声为主,如何有效压制运动噪声是一个较大的挑战。传统的数字滤波只能滤除指定频段的噪声,对于混叠在全张量磁力梯度有用信号中的噪声不能有效分离。鉴于卡尔曼滤波是一种快速、高效和实时的最优估计方法,笔者将其应用到航空全张量磁力梯度数据处理中,搭建合理的状态方程和观测方程,通过模型实验验证了方法的有效性,结果显示全区噪声衰减因子优于0.92,即能够去除92%以上噪声成分,全区均方误差优于10 pT/m,可应用于航空全张量磁力梯度数据实时处理。

关键词： 全张量磁力梯度 ; 卡尔曼滤波 ; 白噪声 ; 数据处理

Abstract

The aero full tensor magnetic gradient data contain complex motion noise, which is distributed from low frequency to high frequency in the spectrum, and is mainly white noise. So, how to effectively suppress the motion noise is a great challenge. The traditional digital filtering can only filter the noise with the specified frequency band, but it can not effectively separate the noise mixed in the full tensor magnetic gradient useful signal. In view of the fact that Kalman filter is a fast, efficient and real-time optimization estimation method, the authors applied it to the aero magnetic full tensor gradient data processing, and built the state equation and observation equation reasonably. Model test proves that the method is effective and can be applied to real-time processing of aeromagnetic full tensor gradient data.

Keywords： full tensor magnetic gradient ; Kalman filter ; white noise ; data processing

PDF (1938KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

孟庆奎, 周坚鑫, 舒晴, 高维, 徐光晶, 王晨阳. 理论模型分析卡尔曼滤波在航空全张量磁力梯度测量中的应用效果. 物探与化探[J], 2021, 45(2): 473-479 doi:10.11720/wtyht.2021.1307

MENG Qing-Kui, ZHOU Jian-Xin, SHU Qing, GAO Wei, XU Guang-Jing, WANG Chen-Yang. Application effect of Kalman filter in airborne full tensor magnetic gradient measurement based on theoretical model. Geophysical and Geochemical Exploration[J], 2021, 45(2): 473-479 doi:10.11720/wtyht.2021.1307

0 引言

实验室条件下,基于超导量子干涉器(superconducting quantum interference device,SQUID)的全张量磁力梯度测量系统的灵敏度可以达到几个fT的量级,能实现对微弱磁性目标体的定位与识别[1,2],为目标探测提供有效手段。21世纪以来,航空全张量磁力梯度测量系统研发及配套数据处理解释理论是国内外相关领域学者研究的热点,德国、美国、澳大利亚等发达国家对全张量磁力梯度测量技术开展了大量探索研发工作。目前,国际上仅德国光学分子研究中心拥有实用化水平的航空全张量磁力梯度测量系统[3],且该技术属于西方国家限制出口的尖端技术,公开的文献资料也非常有限。面对技术封锁,我国自力更生,在“国家重大科研装备研制项目”和“国家863计划”支持下,中国科学院上海微系统与信息技术研究所及吉林大学研发团队分别研制出基于低温和高温SQUID的航空全张量磁力梯度测量系统,研发团队攻克了串扰、平台震动监测、磁张量补偿等多项技术难关[4,5,6,7,8,9],取得了长足进步,但离实用化还存在一定的差距。我国学者在全张量磁力梯度数据处理[10,11]、正反演[12,13,14,15]、综合应用[16,17,18,19]等方面也取得了系列成果。

航空全张量磁力梯度测量数据中包含非常复杂的运动噪声,在频谱图中从低频至高频均有分布,并以白噪声为主,如何有效压制运动噪声是一个较大的挑战[3]。Stolz R总结了运动噪声来源,包括仪器本身几何位置变化、外部环境噪声、飞机发动机噪声以及仪器本证噪声[3],航磁软补偿技术可以去除运动载体在地磁场中产生的恒定磁场、感应磁场和涡流磁场等干扰场[20],对于白噪声却是无能为力。传统的数字滤波只能滤除指定频段的噪声,对于混叠在全张量磁力梯度有用信号中的噪声不能有效分离。卡尔曼滤波技术在航空重力测量中得到了应用,实践表明,该方法可以有效提取淹没在载体高频振动噪声中的有用信号[21,22,23],将其推广应用到航空全张量磁力梯度数据处理中十分必要。张兴东将卡尔曼滤波应用到全张量磁力梯度数据处理中[9],但是没有明确状态方程和观测方程的搭建方式,而不合理的状态方程会直接影响到卡尔曼滤波效果。笔者借鉴时间序列分析思想,基于最小差分方差建立状态方程,并将卡尔曼滤波与数字滤波相结合,通过模型计算验证了方法的有效性,全区噪声衰减因子优于0.92,即能够去除92%以上噪声成分,全区均方误差优于10 pT/m,满足航空全张量磁力梯度测量精度要求。卡尔曼滤波是一种快速、高效的递推算法,利用实时测量信息对估计值进行最优估计,可直接应用于航空全张量磁力梯度测量实时数据处理。

1 卡尔曼滤波方程建立

1.1 卡尔曼滤波基本理论

滤波估计经历了最小二乘、温纳滤波和卡尔曼滤波的发展而不断完善。1960年,卡尔曼提出离散系统卡尔曼滤波,次年与布西合作,将这种滤波方法推广到连续时间系统中,从而形成了卡尔曼滤波设计理论[24]。卡尔曼滤波是一种时间域滤波方法,采用状态空间方法描述系统,算法采用递推形式,数据存储量小,不仅可以处理平稳随机过程,也可以处理多维和非平稳随机过程。

卡尔曼滤波采用如下空间模型描述动态系统:

X(k)=ΦX(k-1)+ΓW(k-1),
Y(k)=HX(k)+V(k),

式中:k 为离散时间,系统在时刻k的状态为X(k);Y(k)为对应状态的观测信号;W(k)为输入的白噪声;V(k)为观测噪声;Φ为状态转移矩阵;Γ为噪声驱动矩阵;H为观测矩阵。式(1)为状态方程,式(2)为观测方程。

卡尔曼滤波递推公式可据射影定理推导。在给定状态量初值 X˙(0)和协方差初值P(0)情况下,依次按照时间更新方程(式(3)、(4))和测量更新方程(式(5)~(7))递推计算,就可以实现对状态变量的卡尔曼滤波最优估计[21],具体递推方程如下:

X˙(k,k-1)=ΦX˙(k-1),
P(k,k-1)=ΦP(k-1)ΦT+ΓQΓT,
K(k)=P(k,k-1)HT[HP(k,k-1)HT+R]-1,
X˙(k)=X˙(k,k-1)+K(k)[Y(k)-HX˙(k,k-1)],
P(k)=[I-K(k)H]P(k,k-1),

式中:Q和R分别为过程噪声和测量噪声的协方差矩阵,I为单位矩阵, X˙(k,k-1)为状态量的一步预测,P(k,k-1)为估计协方差矩阵的一步预测,K(k)为k时刻的滤波增益矩阵, X˙(k)为k时刻的状态估计,P(k)为k时刻的估计协方差矩阵。由此可见,由k时刻的测量值Y(k),实时推估了k时刻的状态估计值 X˙(k)。

1.2 全张量磁力梯度数据卡尔曼滤波方程建立

全张量磁力梯度仪在每个采样点测量6个梯度值,定义卡尔曼滤波器的状态序列为:

X=(Bxx,Bxy,Bxz,Byy,Byz,Bzz)T,

各个测量时刻的测量序列为:

Z=(Bxx,Bxy,Bxz,Byy,Byz,Bzz)T,

因为测量序列与状态序列变量相同,所以可以容易的定义观测矩阵为:

H=diag(1,1,1,1,1,1),

式中:diag表示对角矩阵。状态转移矩阵Φ的定义是一个难点,因全张量磁力梯度仪测量的数据是随时间变化的变量,故可借鉴时间序列分析思想,计算包含白噪声的梯度测量值的各阶次差分方差,方差最小的阶次差分的残差可视为白噪声,根据该阶次差分方程可构建状态方程。经大量模型计算,一阶差分方差最小,故可定义状态转移矩阵为:

　　Φ=diag(1,1,1,1,1,1)。

本文中卡尔曼滤波进行迭代的本质是利用两个正态分布的融合仍是正态分布的特性而进行的,所指的两个正态分布分别为系统输入噪声和测量噪声的正态分布,系统输入噪声是指我们建立的系统状态方程本身存在的系统误差,测量噪声是指测量仪器精度、外界温度变化等因素产生的测量误差。融合后的正态分布所选择的权值是指卡尔曼增益矩阵,其计算公式可参见式(5)。

2 模型算例分析

2.1 球体模型正演

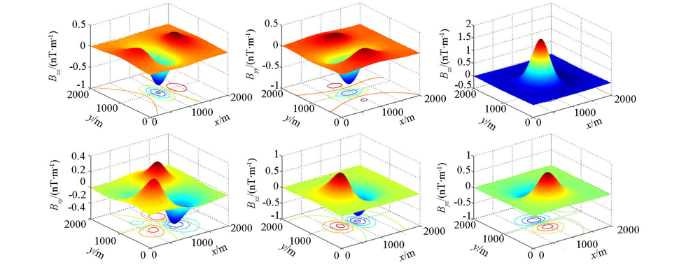
自然界中存在诸多尺度有限的磁性地质体,当其中心埋深远远大于其直径时,地质体所引起的磁异常特征与球体磁场特征基本吻合,所以研究球体的磁场特征具有一定的实际意义。根据重磁位泊松公式,由引力位计算磁场三分量,进而对磁场三分量在3个不同方向(X、Y、Z)求导便可得到球体的全张量梯度。

模型参数:测区范围2 000 m×2 000 m,测量间距5 m,球心位置(1 000 m,1 000 m,550 m),球体半径500 m,总磁化强度倾角65°,偏角11°,总磁化强度0.5 A/m。正演模拟结果见图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   球体模型全张量磁力梯度

Fig.1   Full tensor magnetic gradient of sphere model


2.2 卡尔曼滤波效果

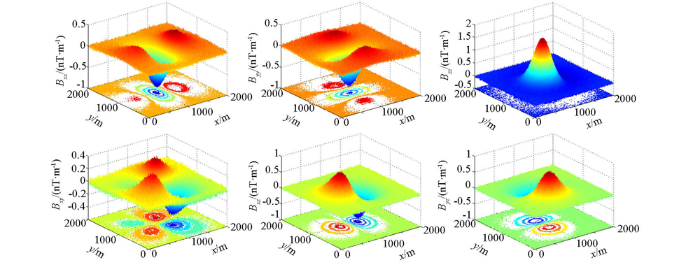
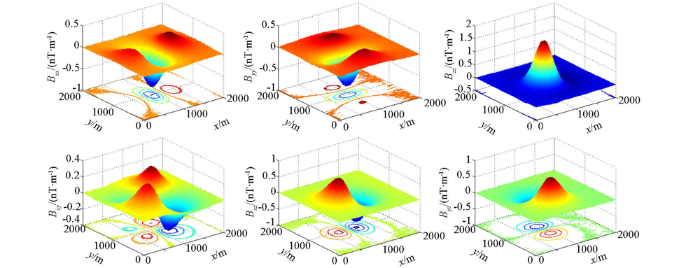
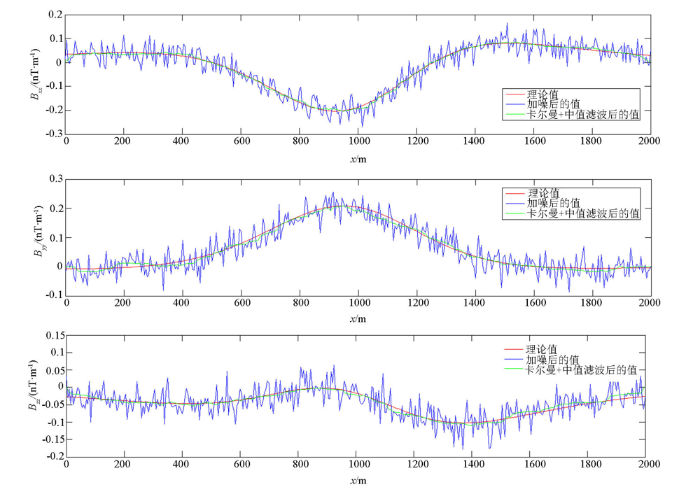
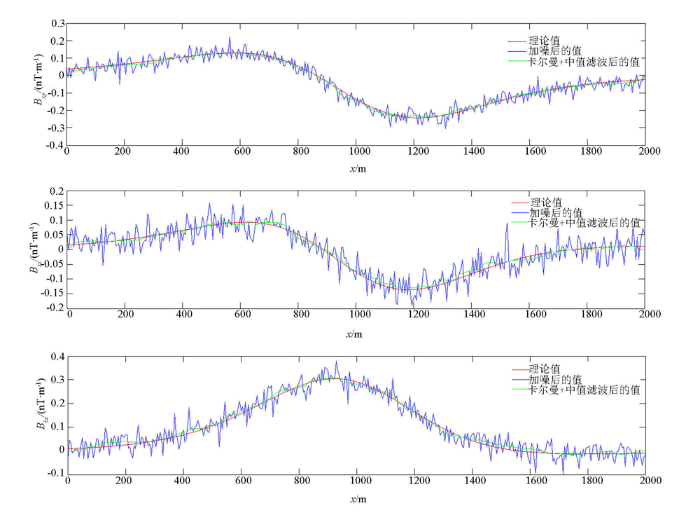
在上述正演结果中加入高斯白噪声V(k),视为观测噪声, V(k)均值为零,标准差为0.032 nT/m。加入噪声的球体模型全张量磁力梯度视为测量值,如图2所示,可见测量结果全区域都受到高斯白噪声影响,且较严重。遵循以上卡尔曼滤波状态方程和测量方程,建立递推公式,对测量结果进行卡尔曼滤波。在具体操作中,为模拟航空全张量磁力梯度实时测量与实时处理,从第1条测线(即剖面Y=0)的第1个测点开始,随着数据的采集,时间的推移,逐点进行卡尔曼滤波处理,直到全部数据采集完毕,同时完成滤波处理,体现了滤波技术的实时性。在不改变异常形态的前提下,为得到更加光滑的滤波效果,卡尔曼滤波后进行小尺度中值滤波,最终的滤波结果见图3~6所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   加噪球体模型全张量磁力梯度

Fig.2   Full tensor magnetic gradient of noisy sphere model


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   滤波后全张量磁力梯度立体图

Fig.3   Filtered full tensor magnetic gradient of sphere model


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   Bxx、Byy和Bzz滤波前后对比(剖面Y=500 m)

Fig.4   Comparison of Bxx ,Byyand Bzz with before and after filtering(profile Y=500 m)


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   Bxy和Bxz和Byz滤波前后对比(剖面Y=500 m)

Fig.5   Comparison of Bxy ,Bxz and Byzwith before and after filtering (profile Y=500 m)


图6

新窗口打开| 下载原图ZIP| 生成PPT

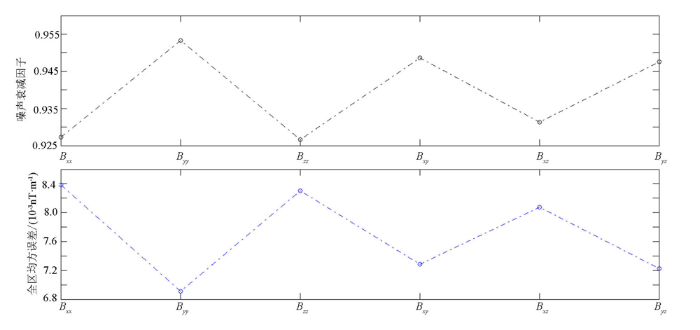
图6   全区噪声衰减因子及全区均方误差

Fig.6   Full area noise-reduction factor and mean square error


为了定量评价本文所提出方法的滤波效果,进一步评价卡尔曼滤波的降噪性能,引入Pajot等[25]定义的噪声衰减因子β来估计噪声衰减量:

β=[var(Bzs-B)-var(Bkf-B)]/var(Bzs-B),

式中:Bzs表示含噪声测量值,B表示理论值,Bkf表示卡尔曼滤波后的值。计算6个梯度张量的全区噪声衰减因子,计算结果见图6a所示,可见β值优于0.92,即能够去除92%以上噪声成分。同时,计算6个梯度张量的全区均方误差,结果见图6b所示,均优于10 pT/m。另外,计算了典型剖面(Y=500 m)上6个梯度张量的噪声衰减因子(0.921 2~0.966 8)和均方误差(6.2~8.5 pT/m),具体结果见表1所示。以上定量评价结果表明,本文所提方法的滤波效果能够满足当前航空全张量磁力梯度测量精度要求。

表1   典型剖面(Y=500 m)卡尔曼滤波效果定量统计

Table 1  Quantitative statistics of Kalman filtering results of typical profile (Y=500 m)

BxxByyBzzBxyBxzByz
噪声衰减因子0.92120.96680.96130.94130.95600.9593
均方误差/(pT·m-1)8.55.76.77.56.66.2

新窗口打开| 下载CSV


3 结论

1) 本文通过理论模型验证了卡尔曼滤波方法在航空全张量梯度测量数据中的有效性,结果显示全区噪声衰减因子优于0.92,全区均方误差优于10 pT/m。

2) 由于因卡尔曼滤波对数据的使用率低及噪声随机特征影响,单纯应用卡尔曼滤波不能得到平滑的预测结果,需要串联其他适合的平滑滤波方法,达到更好的滤波效果。

3) 卡尔曼滤波可以利用实时测量信息对估计值进行最优估计,具备快速、高效的递推特性,建议应用于航空全张量磁力梯度实时测量数据处理,也可为其他航空地球物理实时测量数据处理提供参考。

参考文献

Gamey T J, Doll W E, Beard L P.

Initial design and testing of a full-tensor airborne SQUID magnetometer for detection of unexploded ordnance

[J]. SEG Technical Program Expanded Abstracts. SEG, 2004, 798-801.

[本文引用: 1]

Schmidt P W, Clark D A.

The magnetic gradient tensor: It̓s properties and uses in source characterization

[J] . The Leading Edge, 2006,25(1):75-78.

DOI:10.1190/1.2164759      URL     [本文引用: 1]

Stolz R, Zakosarenko V, Schulz M, et al.

Magnetic full tensor SQUID gradiometer system for geophysical applications

[J]. The Leading Edge, 2006,25(2):178-180.

[本文引用: 3]

申茂冬.

高温超导全张量磁梯度测量技术研究

[D]. 长春:吉林大学, 2017.

[本文引用: 1]

Shen M D.

Study on technology for high temperature superconducting full tensor magnetic gradient measurement

[D]. Changchun: Jilin University, 2017.

[本文引用: 1]

申茂冬, 程德福, 安战峰, 等.

五棱台式全张量磁梯度探头侧面倾角优化方法

[J]. 吉林大学学报:工学版, 2016,46(5):1732-1738.

[本文引用: 1]

Shen M D, Chen F D, An Z F, et al.

Optimization of slanting surfaces of five-sided pyramidal full tensor magnetic gradient probe

[J]. Journal of Jilin University:Engineering and Technology Edition, 2016,46(5):1732-1738.

[本文引用: 1]

伍俊, 荣亮亮, 孔祥燕, 等.

基于Cortex-M3的航空超导磁测量平台振动监测仪

[J]. 仪表技术与传感器, 2016,(1):22-25.

[本文引用: 1]

Wu J, Rong L L, Kong X X, et al.

Vibration monitor based on cortex-m3 for aviation superconducting magnetic measurement platform

[J]. Instrument Technique and Sensor, 2016,(1):22-25.

[本文引用: 1]

伍俊, 邱隆清, 孔祥燕, 等.

基于GPS同步的新型低温超导磁力仪

[J]. 传感器技术学报, 2015,28(9):1347-1353.

[本文引用: 1]

Wu J, Qiu L Q, Kong X X, et al.

A novel low temperature SQUID magnetometer based on GPS synchronization

[J]. Chinese Journal of Sensors and Actuators, 2015,28(9):1347-1353.

[本文引用: 1]

王士良, 邱隆清, 王永良, 等.

航空超导全张量磁梯度仪的串扰研究

[J]. 低温物理学报, 2017,39(1):36-40.

[本文引用: 1]

Wang S L, Qiu L Q, Wang Y L, et al.

Study on Crosstalk of an airborne magnetic full tensor SUQID gradiometer system

[J]. Chinese Journal of Low Temperature Physics, 2017,39(1):36-40.

[本文引用: 1]

张光, 张英堂, 尹刚, 等.

一种磁张量探测系统载体的磁张量补偿方法

[J]. 地球物理学报, 2016,59(1):311-317.

[本文引用: 2]

Zhang G, Zhang Y T, Yin G, et al.

Magnetic tensor compensation method for the carrier of the magnetic tensordetection system

[J]. Chinese J. Geophys., 2016,59(1):311-317.

[本文引用: 2]

张兴东.

卡尔曼滤波在全张量磁梯度数据处理中的应用

[D]. 北京:中国地质大学(北京), 2015.

[本文引用: 1]

Zhang X D.

Application of Kalman Filtering in the magnetic full tensor gradiometer data processing

[D]. Beijing: China University of Geosciences(Beijing), 2015.

[本文引用: 1]

舒晴, 马国庆, 刘财, 等.

全张量磁梯度数据解释的均衡边界识别及深度成像技术

[J]. 地球物理学报, 2018,61(4):1539-1548.

[本文引用: 1]

Shu Q, Ma G Q, Liu C, et al.

Balanced edge detection and depth imaging technique for the interpretation of full tensor magnetic gradient data

[J]. Chinese J. Geophys., 2018,61(4):1539-1548.

[本文引用: 1]

骆遥, 姚长利.

长方体磁场及其梯度无解析奇点表达式理论研究

石油地球物理勘探, 2007,42(6):714-719.

[本文引用: 1]

Luo Y, Yao C L.

Theoretical study on cuboid magnetic field and gradient expression without singular point

[J]. Oil Geophysical Prospecting, 2007,42(6):714-719.

[本文引用: 1]

钟炀, 管彦武, 石甲强, 等.

利用IGRF 模型计算全张量地磁梯度

[J]. 物探与化探, 2020,44(3):582-590.

[本文引用: 1]

Zhong Y, Guan Y W, Shi J Q, et al.

The calculation method of full tensor geomagnetic gradient based on IGRF model

[J]. Geophysical and Geochemical Exploration, 2020,44(3):582-590.

[本文引用: 1]

钟炀, 管彦武, 石甲强, 等.

长方体全张量磁梯度的两种正演公式对比

[J]. 世界地质, 2019,38(4):1073-1081,1090.

[本文引用: 1]

Zhong Y, Guan Y W, Shi J Q, et al.

Comparison of two forward modeling formulas for full tensor magnetic gradient of cuboid

[J]. Global Geology, 2019,38(4):1073-1081,1090.

[本文引用: 1]

周德文, 孟庆奎, 杨怡, 等.

航磁全轴梯度异常特征研究

[J]. 物探与化探, 2018,42(3):583-588.

[本文引用: 1]

Zhou D W, Meng Q K, Yang Y, et al.

Study on characteristics of three axis airborne magnetic gradient anomaly

[J]. Geophysical and Geochemical Exploration, 2018,42(3):583-588.

[本文引用: 1]

Ji S X, Zhang H, Wang Y F, et al.

Three dimensional inversion of full magnetic gradient tensor data based on hybrid regularization method

[J]. Geophysical Prospecting, 2019,67(1):226-261.

[本文引用: 1]

吴招才.

磁力梯度张量技术及其应用研究

[D]. 武汉:中国地质大学(武汉), 2008.

[本文引用: 1]

Wu Z C.

Magnetic gradient tensor technology and its application

[D]. Wuhan: China University of Geosciences(Wuhan), 2008.

[本文引用: 1]

郑婷.

全张量 SQUID磁梯度计在航空磁测方面的应用研究

[J]. 超导技术, 2015,43(10):41-44.

[本文引用: 1]

Zheng T.

Research on application of airborne magnetometry using full tensor squid gradiometer

[J]. Superconductivity, 2015,43(10):41-44.

[本文引用: 1]

Luo Y, Wu M P, Wang P, et al.

Full magnetic gradient tensor form triaxial aero magnetic gradient measurements: Calculation and application

[J]. Applied Geophysics, 2015,12(3):283-291.

[本文引用: 1]

孟庆奎, 周德文, 高维, 等.

国内外航磁补偿技术历史与展望

[J]. 物探与化探, 2017,41(4):694-699.

[本文引用: 1]

Meng Q K, Zhou D W, Gao W, et al.

History and prospects of aeromagnetic compensation technologies used in China and abroad

[J]. Geophysical and Geochemical Exploration, 2017,41(4):694-699.

[本文引用: 1]

王静波, 熊盛青, 郭志宏, 等.

航空重力数据Kalman滤波平滑技术应用研究

[J]. 地球物理学进展, 2012,27(4):1717-1722.

[本文引用: 2]

Wang J B, Xiong S Q, Guo Z H, et al.

Application of Kalman filtering smoothing technique for aeronautical gravity data

[J]. Progressin Geophysics, 2012,27(4):1717-1722.

[本文引用: 2]

蔡体菁, 周薇, 鞠玲玲.

平台式重力仪测量数据的卡尔曼滤波处理

[J]. 中国惯性技术学报, 2015,23(6):718-720.

[本文引用: 1]

Cai T J, Zhou W, Ju L L.

Kalman filter processing of platform gravimeter measurement data

[J]. Chinese Journal of Inertial Technology, 2015,23(6):718-720.

[本文引用: 1]

罗锋, 王冠鑫, 周锡华, 等.

三轴稳定平台式航空重力测量数据处理方法研究与实现

[J]. 物探与化探, 2019,43(4):872-880.

[本文引用: 1]

Luo F, Wang G X, Zhou X H, et al.

Research and implementation of data processing method for the three-axis stabilized platform airborne gravity measuring system

[J]. Geophysical and Geochemical Exploration, 2019,43(4):872-880.

[本文引用: 1]

Grewal M S, Andrews A P.

Kalman filtering theory and practice using MATLAB

[M]. New York: Wiley, 2008: 133-138.

[本文引用: 1]

Pajot G, Viron O D, Diament M, et al.

Noise reduction through joint processing of gravity and gravity gradient data

[J]. Geophysics, 2008,73(3):I23.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com