关于浮动基准面与起伏地表面的讨论

doi:10.11720/wtyht.2021.2557

关于浮动基准面与起伏地表面的讨论

徐蔚亚^,

中国石油化工股份有限公司石油勘探开发研究院,北京 100083

Discussion on floating datum and rugged topography

XU Wei-Ya^,

Sinopec Petroleum Exploration and Production Research Institute,Beijing 100083,China

责任编辑: 叶佩

收稿日期: 2019-12-10 修回日期: 2020-09-10 网络出版日期: 2021-02-20

基金资助:

国家科技重大专项. 2017ZX05005-004
中石化科技部项目. P17021-4

Received: 2019-12-10 Revised: 2020-09-10 Online: 2021-02-20

作者简介 About authors

徐蔚亚(1974-),男,毕业于同济大学固体地球物理专业,长期从事地震资料信号处理与偏移成像领域的生产和研究工作。Email:xuwy.syky@sinopec.com

摘要

确定起伏地表的空间位置是叠前深度域起伏地表偏移成像和速度建模成功的关键。浮动基准面本身就是一个起伏高程面,此外它还定义了CMP道集在其上进行基准面校正的规则。本文分析了确定浮动基准面的常用方法并明确了其在一般情况下所具有的物理意义,指出了即便是基于平均静校正法得到的浮动基准面,在一定条件下也可以直接用于起伏地表叠前深度域偏移成像和速度建模。此外,还讨论了在叠前深度域速度建模中错误地使用浮动基准面数据可能导致深度域成像结果中层位深度的移位和畸变的问题。

关键词： 浮动基准面 ; 起伏地表 ; 平均静校正量法 ; 速度建模 ; 叠前深度偏移 ; 叠前时间偏移

Abstract

Determination of the spatial position of the rugged topography surface is the key to the success of the pre-stack depth migration and velocity modeling on relief surface.The floating datum is not only a rugged topography elevation surface,but also defines the rules on which the CMP gathers are used for datum corrections.Analyzed the definition of the floating datum and clarified the physical meaning of the floating datum in general situations.The seismic data and velocity on floating datum can be directly used for topography pre-stack depth migration and velocity modeling under specific conditions.Discussed the situation that the improper use of floating datum data and corresponding RMS velocity in pre-stack depth migration and velocity modeling might result in shifting and distortion of the horizon layers in depth migration results.

Keywords： floating datum ; rugged topography ; average statics methods ; velocity modeling ; pre-stack depth migration ; pre-stack time migration

PDF (1266KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

徐蔚亚. 关于浮动基准面与起伏地表面的讨论. 物探与化探[J], 2021, 45(1): 95-101 doi:10.11720/wtyht.2021.2557

XU Wei-Ya. Discussion on floating datum and rugged topography. Geophysical and Geochemical Exploration[J], 2021, 45(1): 95-101 doi:10.11720/wtyht.2021.2557

0 引言

当地表起伏不大,并且近地表速度变化不大时,在固定基准面上进行地震资料处理可以得到较好的结果。但在地表存在较大起伏和复杂近地表构造的地区,为了在速度分析和叠加时消除变化的起伏地表、近地表速度横向变化的影响,同时又需要使拾取反射波速度的t₀时间接近原始记录的t₀时间,以尽量满足地下反射信号的同相叠加^[1],需要在浮动基准面上进行速度分析和叠加,以减少静校正误差和防止假构造的出现^[2,3]。

随着探区近地表及地下构造复杂程度的增加,基于固定基准面的偏移成像技术逐渐无法满足地震勘探对偏移成像的精度要求。当前,浮动基准面处理已经是地震资料时间域处理的常规步骤之一^[4,5,6]。随着叠前时间偏移和深度偏移成像技术的发展^[7],基于起伏地表的叠前时间偏移及叠前深度偏移成像技术开始得到广泛的研究和应用^[8,9],甚至在地表起伏剧烈、近地表横向变速严重、地下构造复杂的地区,直接从真地表小平滑面开始进行叠前深度域的速度建模和成像,以解决常规处理中复杂近地表中存在的静校正问题^[10,11,12]。从浮动基准面数据(地震数据和解释的时间域均方根速度)到起伏地表深度建模的转换也有很多有益的思路^[10]。特别是林伯香^[13]指出了RG值应是等效低速带的静校正量,分析了浮动基准面的物理意义,指出了常速近地表、水平高速顶界面情况下平滑地表高程就是浮动基准面对应的高程面,但并未进一步指出一般情况下确定其空间位置的办法。同时,很多地震资料处理人员由于对浮动基准面存在一些误解,习惯了时间域浮动基准面的处理方式,在从常规时间域处理向叠前深度域建模和偏移转换的过程中常常为浮动基准面和起伏地表的转换感到困惑。本文详细解释了浮动基准面的概念及其物理含义,指出其对应的高程面可以视作一个起伏地表面,并且在特殊情况下浮动基准面对应的高程面就是地表高程的平滑面;利用浮动基准面对应的高程面,时间域分析得到的均方根速度在时深转换后也可以直接用作叠前深度偏移的初始速度;为将时间域的浮动基准面处理和深度域的起伏地表处理结合在一起提供了有益的参考。

1 静校正的计算

对于地表一致性静校正,假设地表由风化层覆盖且风化层的速度较低,地震波在风化层中沿垂直方向传播,此时炮点或检波点位置处的静校正量可理解为先剥去地震波在低降速带中的传播时间,再增加从高速层顶界面到最终基准面,以替换速度传播的时间^[14],该过程可通过式(1)表示:

(1)

t = - \frac{E_{s} - E_{h}}{V_{low}} + \frac{E_{d} - E_{h}}{V_{rep}}

式中:t为某位置处的静校正量;E_s为该位置对应的地表高程;E_h为该位置在地下对应的高速顶界面的高程;E_d为最终基准面高程;V_low为该位置对应的低降速带等效速度;V_rep为替换速度。

对于一个地震道来说,静校正量包含两部分,即炮点处的静校正量和检波点处的静校正量。当近地表速度存在横向变化时,根据式(1)可得到一个地震道的总的静校正量T_i为:

(2)

T_{i} = t_{i, s} + t_{i, g} = - (\frac{E_{i, s, s} - E_{i, h, s}}{V_{i, low, s}} + \frac{E_{i, s, g} - E_{i, h, g}}{V_{i, low, g}}) + (\frac{E_{d} - E_{i, h, s}}{V_{rep}} + \frac{E_{d} - E_{i, h, g}}{V_{rep}})

式中:t_i_,s为炮点处的静校正量;t_i_,g为检波点处的静校正量;E_i_,s,s为炮点高程;E_i_,h,s为炮点位置对应的地下高速顶界面高程;E_i_,s,g为检波点高程;E_i_,h,g为检波点处对应的地下高速顶界面的高程;V_i_,low,s为炮点处对应的地下低降速带的等效速度;V_i_,low,g表示检波点处对应的地下低降速带的等效速度。

2 浮动基准面

2.1 浮动基准面的概念

在地表起伏较大的地区,地震资料处理常常在浮动基准面进行^[15]。这里的浮动基准面是一个基准面高程可以随空间位置变化的参考面^[16],主要用来降低地表起伏较大时,采用地震波在近地表垂直传播的假设而导致的误差。和固定基准面相比,浮动基准面有以下几个特点:

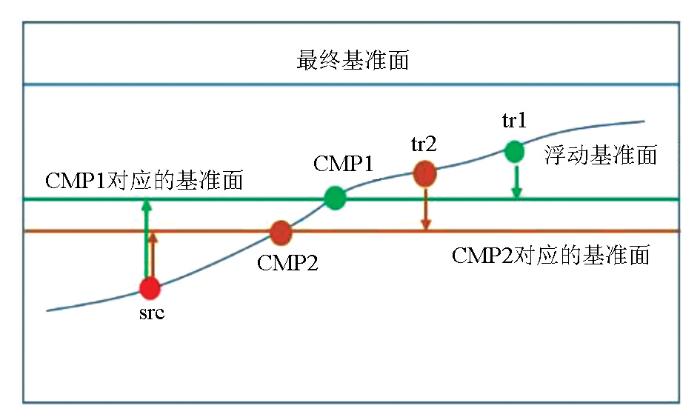
1)浮动基准面对应的高程面是随空间变化的(图1中的浮动基准面);

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 相同炮点在不同CMP道集中的基准面位置

Fig.1 Datum position of the same source in different CMP gathers

2)浮动基准面不仅仅是一个高程面,还定义了地震数据在该参考面上处理基准面的规则,目前该规则主要用于CMP道集数据;

3)在浮动基准面上,同一个CMP道集内的所有地震道的炮点、检波点都在该CMP对应的浮动基准面高程上;

4)浮动基准面上的地震数据,即便是相同炮点、检波点,其基准面在不同CMP道集中对应的高程可以是不同的,是随着CMP点在浮动基准面上的高程值变化而变化的。也即,炮点、检波点的基准面是随CMP浮动的,但在一个CMP内又是相同的(浮动基准面名称的由来),由此来保证时间域中速度分析、剩余静校正、叠加等常规处理方法所需要的水平地表的假设条件。

图1中,src为炮点,tr1和tr2分别为该炮中的两个地震道,这两道对应的CMP分别为CMP1和CMP2,炮点在CMP1中的基准面为绿色线定义的基准面,在CMP2中的基准面为棕色线定义的基准面。基于相同的原理,相同检波点位置,在不同CMP道集中的基准面也可以是不同的,如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 相同检波点在不同CMP道集中的基准面位置

Fig.2 Datum position of the same detector in different CMP gathers

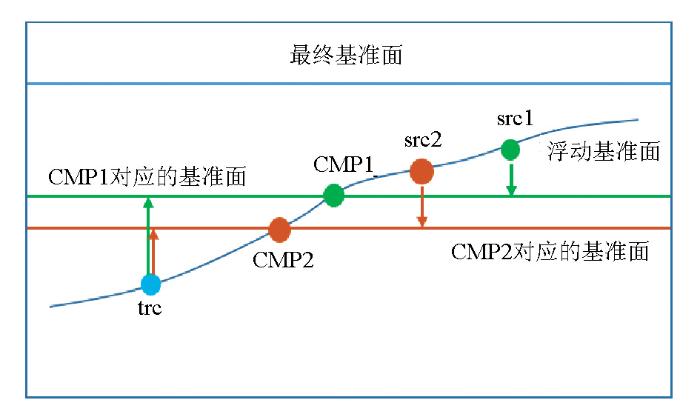
在图2中,trc为检波点,src1和src2分别为包含该检波点上地震道的两个震源,这两个震源对应的CMP分别为CMP1和CMP2,检波点trc在CMP1中的基准面为绿色线定义的基准面,在CMP2中的基准面为棕色线定义的基准面。

2.2 浮动基准面的确定

根据前面所述浮动基准面的特点可知,浮动基准面可以由一个起伏的高程面和在地震数据中处理基准面的规则所定义,因此确定浮动基准面主要就是确定起伏的高程面。在实际地震资料处理中,常用的浮动基准面确定方法可分为两类,一类通过直接计算浮动基准面对应的起伏高程面来确定^[17],另一类通过对静校正量的计算来确定^[15,18]。前者包括平滑地表高程法、平滑低速带底面法、人为给定法以及最小静校正误差浮动基准面法,后者主要是平均静校正量法。

第一类中的4种方法都直接确定了浮动基准面对应的高程面,其物理意义明确,为了将地震数据校正到浮动基准面,需要计算每一个CMP道集从浮动基准面到最终基准面的校正时间,设某个CMP的校正时间为t_cmp,则其计算公式为:

(3)

t_{cmp} = \frac{2 (E_{d} - E_{cmp})}{V_{rep}}

式中:E_d为最终基准面高程;E_cmp为该CMP对应的浮动基准面高程;V_rep为计算静校正使用的替换速度。为了将地震数据校正到浮动基准面,首先需要将所有炮点、检波点上的静校正全部应用,将数据校正到最终基准面,然后将每个CMP道集的时间减掉相应的t_cmp,即可完成浮动基准面校正。

第二类中的平均静校正量法也即是两步法静校正中使用的方法,它是通过先将静校正量分解成高频量和低频量,再在数据中应用高频量但保留低频量而实现浮动基准面校正。其中的低频量就是CMP道集内的平均静校正量,也是从浮动基准面向固定基准面校正的时间量;其中的高频量为每道的静校正量和该道对应的CMP平均静校正量之差。假设近地表模型为横向变速模型,炮点、检波点均在地表,为了计算一个CMP道集内的平均静校正量t_cmp(由于平均静校正量即为从浮动基准面向固定基准面的校正量,故在此使用相同的符号),由式(2)可得:

(4)

t_{cmp} = \frac{1}{n} \overset{n}{\sum_{i = 1}} T_{i} = \frac{1}{n} \overset{n}{\sum_{i = 1}} (t_{i, s} + t_{i, g}) = \frac{1}{n} \overset{n}{\sum_{i = 1}} [- (\frac{E_{i, s, s} - E_{i, h, s}}{V_{i, low, s}} + \frac{E_{i, s, g} - E_{i, h, g}}{V_{i, low, g}}) + (\frac{E_{d} - E_{i, h, s}}{V_{rep}} + \frac{E_{d} - E_{i, h, g}}{V_{rep}})]

式中:n为CMP道集中的总道数;i为CMP道集中的第i道;t_i_,s为第i道对应的炮点静校正量;t_i_,g为第i道对应的检波点静校正量;E_i_,s,s为第i道对应的炮点地表高程;E_i_,h,s为第i道对应的炮点位置高速顶界面的高程;V_i_,low,s为第i道对应的炮点处近地表等效速度;E_i_,s,g为第i道对应的检波点地表高程;E_i_,h,g为第道对应的检波点位置高速顶界面的高程;V_i_,low,g为第i道对应的检波点处近地表等效速度;E_d为最终基准面;V_rep为计算静校正使用的替换速度。

平均静校正量法通过时间量的校正实现了地震数据由地表到浮动基准面的校正,整个过程与高程无关,虽然难以直接观察到对应的起伏地表面,但由于该方法计算简单使用方便,因此广泛用于常规时间域处理中。

由于该方法不直接计算起伏高程面,而是通过计算CMP位置上炮、检点静校正量的平均值来实现地震数据从地表到浮动基准面的校正,因此很多地震资料处理人员直接将该平均静校正量当作浮动基准面,这样的认识其实是不准确的,平均静校正量仅仅是从浮动基准面向最终基准面校正的一个时间量。对浮动基准面错误的理解,会在地震资料处理从时间域向深度域发展、从浮动基准面处理向起伏地表建模与成像转换的过程中造成概念上的混淆和迷惑。

2.3 浮动基准面对应的高程面

如果浮动基准面是通过起伏的高程面来确定的,那么该浮动基准面的空间位置是确定的,本文不再介绍。如果浮动基准面是通过平均静校正量法得到的,由于计算过程不涉及高程,因此无法直接得到浮动基准面的空间位置,但这不意味着浮动基准面不存在。事实上,刘治凡和林伯香^[1,13]指出了在一定情况下,浮动基准面对应的高程面就是地表高程的平滑面,但并未指出一般情况下确定其空间位置的办法。本文将通过一个更具代表性的、存在横向变速的模型,通过分析应用在数据上的高频分量,讨论存在横向变速情况下确定平均静校正量法浮动基准面对应的高程面的方法。

为了将地震数据校正到浮动基准面上,在得到每个CMP位置的平均静校正量之后,需要对每一个地震道进行校正,校正的时间量为每个地震道上的总校正量和平均校正量之差,也即两步法静校正中的高频量:t_i=T_i-t_cmp。将式(2)和式(4)代入该式并整理得到:

(5)

t_{i} = (- \frac{E_{i, s, s} - E_{i, h, s}}{V_{i, low, s}} + \frac{1}{n} \overset{n}{\sum_{j = 1}} \frac{E_{j, s, s} - E_{j, h, s}}{V_{j, low, s}}) + (- \frac{E_{i, s, g} - E_{i, h, g}}{V_{i, low, g}} + \frac{1}{n} \overset{n}{\sum_{j = 1}} \frac{E_{j, s, g} - E_{j, h, g}}{V_{j, low, g}}) + \frac{2}{V_{rep}} (\frac{2 E_{d} - E_{i, h, s} - E_{i, h, g}}{2} - \frac{1}{n} \overset{n}{\sum_{j = 1}} \frac{2 E_{d} - E_{j, h, s} - E_{j, h, g}}{2})

此处,下标j表示CMP道集中的某一道。在式(5)中,高频量跟道集中每一道的地表高程、高速顶界面高程、低降速带速度与替换速度有关,确实难以直接判断出浮动基准面的空间位置。但考虑到在计算静校正量时,一般会在近地表速度模型中选择足够平滑的高速顶界面,因此,当高速顶界面的起伏较小时,如果能在一个CMP道集的范围内将其视为水平面,并以E_h来表示其高程,则式(5)可以简化为:

(6)

t_{i} = - (\frac{E_{i, s, s} - E_{h}}{V_{i, low, s}} + \frac{E_{i, s, g} - E_{h}}{V_{i, low, g}}) + \frac{1}{n} \overset{n}{\sum_{j = 1}} (\frac{E_{j, s, s} - E_{h}}{V_{j, low, s}} + \frac{E_{j, s, g} - E_{h}}{V_{j, low, g}})

此时,高频量的计算只跟地表高程、高速顶界面以及低降速带中的速度有关,跟替换速度和最终基准面无关。

再假设存在一个背景参考速度V_ref,ΔV_i_,s为第i道上的速度扰动,令R_i_,s= $\frac{V_{ref}}{V_{ref} + Δ V_{i, s}}$ 表示为第i道炮点位置上低降速带等效速度的变化率,R_i_,g= $\frac{V_{ref}}{V_{ref} + Δ V_{i, g}}$ 表示为第i道检波点位置上低降速带等效速度的变化率,d_i_,s=(E_i_,s,s-E_h)为该道在炮点对应的低降速带厚度,d_i_,g=(E_i_,s,g-E_h)为该道在检波点对应的低降速带厚度,则式(6)可变为:

(7)

t_{i} = \frac{2}{V_{ref}} [- (\frac{d_{i, s} R_{i, s} + d_{i, g} R_{i, g}}{2}) + \frac{1}{n} \overset{n}{\sum_{j = 1}} (\frac{d_{j, s} R_{j, s} + d_{j, s} R_{j, g}}{2})]

式(7)说明此时的高频量只与低降速带的厚度、参考速度及局部速度异常有关。如果参考速度V_ref介于低降速带中的最大和最小速度之间,那么等效速度变化率R取值在1附近,式中每一个炮点、检波点的低降速带厚度和速度变化率的乘积可以视为消除局部速度异常后的新厚度,将其叠加在高速顶界面之上,成为重构的地表高程面。这样,式(7)可以粗略地估计为地震波在两个重构的低降速带所对应的地层厚度差之间的双程传播时间,其中一个地层厚度为地震道在重构的低降速带中的平均厚度(根据炮点、检波点位置对应的厚度计算得到),另一个为该CMP道集中所有地震道在重构的低降速带中的平均厚度。考虑到高速顶界面接近水平,上述估计可以大致表述为地震波在地震道平均高程和CMP道集平均高程之间的传播时间差。当参考速度V_ref确定时,式(7)中的第二个求和项对于一个CMP道集来说是不变的,可以看作在该CMP上进行基准面校正的参考值,也即浮动基准面在该CMP上对应的空间位置,此时参考速度V_ref可留给速度分析或速度建模使用。

再进一步,如果近地表速度模型足够简单,如低降速带的速度不存在横向变化,其等效速度可以表示为V_low,则式(6)可简化为:

(8)

t_{i} = \frac{2}{V_{low}} [- \frac{E_{i, s, s} + E_{i, s, g}}{2} + \frac{1}{n} \overset{n}{\sum_{j = 1}} (\frac{E_{j, s, s} + E_{j, s, g}}{2})]

式中求和项得到的是CMP内所有炮点、检波点高程的平均值。在这种情况下,高频量的获得就是基于地震道在检波点和炮点处的平均高程、CMP处的平均高程与低降速带速度计算得到的,将高频量应用于数据上得到浮动基准面数据,此时浮动基准面对应的高程面就是CMP内各道的地表高程平滑面。

3 起伏地表面

在传统的地震资料处理流程中,静校正及浮动基准面常用于时间域的速度分析、剩余静校正、叠加等环节,叠后偏移需要在固定基准面进行。随着勘探难度的增加,基于固定面的偏移成像技术由于在地表起伏剧烈和复杂近地表地区会产生较大误差,基于起伏地表的叠前偏移成像技术逐步得到了广泛的研究和应用^[3,19]。

起伏地表面在目前的地震资料处理与成像中一般指平滑的地表高程面。基于起伏地表的地震资料处理技术,包括叠前时间偏移、叠前深度偏移以及深度域速度建模,首先都需要确定起伏地表面,并将炮点和检波点的位置放置在起伏地表面上。当前,关于起伏地表的确定有不同的方法,如最小静校正误差浮动基准面^[17],该面的空间位置是确定的,因此既可以在该面上对数据进行浮动基准面相关的时间域处理,又可以用于基于起伏地表的叠前偏移成像和深度域速度建模;还有的使用尽可能接近真地表的光滑面作为叠前偏移成像的起伏地表面,并较好地实现了山前带成像^[20];或者采用小距离平滑获得接近真地表的平滑基准面,在此基础上进行拟真地表叠前深度建模与成像技术^[19]。

4 从浮动基准面处理到起伏地表偏移和成像的方法和存在的问题

如2.1节所述,浮动基准面本身就定义了一个起伏高程面,因此理论上浮动基准面数据在从常规时间域处理到叠前深度偏移与建模的转换过程中存在天然的优势。但是在实际生产中,两者往往是分开进行的,时间域的均方根速度在浮动基准面上分析,深度域中的速度建模在重新定义的一个起伏地表面上进行,由于两者的高程面可能不同,时间域中分析得到的均方根速度往往无法直接在深度域中使用。但是这是否意味着浮动基准面无法用于起伏地表偏移成像和建模呢?

根据2.2节所述的浮动基准面的确定方法,如果浮动基准面是通过第一类方法确定的,即首先定义了起伏地表面,那么该面是可以直接用于起伏地表叠前偏移和建模的。比如,如果给定的是第一类浮动基准面上的地震数据,可以根据式(3)将浮动基准面上每一个CMP对应的高程E_cmp反算出来,其计算公式为:

(9)

E_{cmp} = E_{d} - \frac{1}{2} t_{cmp} V_{rep}

如果浮动基准面是通过第二类方法,即通过平均静校正量法得到的,此时浮动基准面对应的起伏地表面不能直接通过式(9)计算。其中的原因可以通过分析高频量计算式(5)~(8)得出:应用在地震数据上的高频量相对于平均静校正量来说很小,仅仅是对部分高程和局部速度异常做了校正,并没有对低降速带进行替换;地震反射的t₀时间也没有过多的改变,数据中还存在有低降速带的影响;甚至在一些特殊情况,如式(6)~(8)所示的情况下,应用在数据中的高频量与最终基准面和替换速度都没有任何关系。因此对于平均静校正浮动基准面上的数据,在上述情况下使用式(9),用最终基准面高程、平均静校正量和替换速度反算浮动基准面的高程是不合理的,此时反算的结果往往会高出地表高程的平滑面。这是因为低降速带越厚、速度越低,t_cmp就越小,计算出来的高程面就会越高。

事实上,根据2.3节的分析可知,部分第二类浮动基准面(平均静校正量法浮动面)对应的高程面的空间位置可以通过高频量的计算公式得到。比如,在式(6)~(8)所依赖的近似条件下,高程面的位置可由公式中的求和项给出。对于存在横向变速、高速层顶界面接近水平的情况,浮动基准面对应的起伏地表面为式(7)中的求和项与高速层顶界面高程之和:

(10)

E_{cmp} = E_{h} + \frac{1}{n} \overset{n}{\sum_{j = 1}} (\frac{d_{j, s} R_{j, s} + d_{j, s} R_{j, g}}{2})

式中:E_cmp为某CMP在浮动基准面上对应的高程;n为CMP道集中的总道数。需要注意的是,E_h为高速顶界面的高程,在从式(5)向式(6)推导过程中曾假设该面是水平的,不过,进一步分析该过程中消除替换速度项的过程可知,只要高速顶界面在一个CMP道集内是呈近似线性变化的,该式都是成立的。这样,式(10)不仅可应用于水平高速顶界面,对于高速顶界面缓慢变化的情况,特别是山前带中地表逐步升高的情况,只要高速顶界面足够平滑,也是适用的。

此时,所有CMP上对应的高程值构成了浮动基准面对应的起伏高程面。需要注意的是,根据这种方法得到的起伏地表面在深度域速度建模中使用时,由于计算平均高程时使用了依赖背景速度场的速度变化率R,因此在起伏地表面和高速顶界面之间应该填充背景速度V_ref。

而对于式(8)所述的水平层状简单情况,第二类浮动基准面对应的高程面为:

(11)

E_{c mp} = \frac{1}{n} \overset{n}{\sum_{j = 1}} (\frac{E_{j, s, s} + E_{j, s, g}}{2})

即浮动基准面对应的高程面为CMP道集内各道炮点、检波点高程的平均值,相当于进行了一个高程校正。

但是,对于第二类浮动基准面,当高速顶界面起伏较大时,高频量由式(5)所定义,此时浮动基准面对应的高程面确实难以估计。这种情况下就无法直接从浮动基准面推算其高程面了,需要采用第一类浮动基准面的确定方法,以便将时间域的处理和深度域的处理结合起来;或者,在起伏地表面上直接进行深度域的建模和成像,此时,时间域的速度成果就无法直接使用了。

5 常见的错误及其分析

在实际地震资料处理过程中,经常使用不同的地震资料处理软件进行时间域的处理和深度域的建模与成像,如果不清楚不同浮动基准面确定方法的区别,就会出现错误的结果。下面通过图示来说明平均静校正量法浮动基准面数据用于深度域建模及成像时容易出现的问题。

假设浮动基准面是通过平均静校正量法得到的,从浮动基准面到固定基准面的校正量为t_cmp,为了便于说明问题,再假设静校正计算时,低降速带引起的静校正剥去量大于使用替换速度的填充量,导致t_cmp<0。

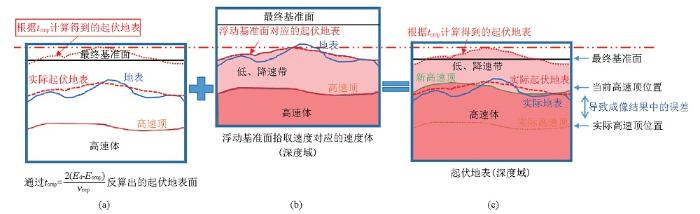
如图3a所示,此时地震道集校正到了浮动基准面,应用的高频量仅仅是对部分高程和速度异常做了校正,没有完成低降速带的替换,低速带的影响还在数据中,对应的起伏地表高程面根据 2.3节的估计在近地表附近(红虚线),但是通过式(9)计算得到的起伏地表面却到了最终基准面之上(红点线)。此时,将浮动基准面中分析得到的均方根速度转换到深度域,其真实的位置应该如图3b所示,但是在建模时会将其填充到图3a中由红点线构成的错误的起伏地表之下,结果如图3c所示。由此造成的结果是,模型中所有地层的高程都被抬高了,如图3c中原本在桔黄色位置的高速顶界面上移到了近地表附近由绿线标识的位置,考虑到这里错误的起伏地表面在计算的过程中还改变了真实起伏地表的形态,因此最终不仅会导致成像结果中的层位在深度上向上移位,层位本身也会出现一定的扭曲。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 错误的起伏地表导致成像结果中出现深度误差

Fig.3 Depth error in migration results from incorrect migration surface

因此当利用浮动基准面数据在深度域中进行建模时,需要首先了解浮动基准面的确定方式。如果浮动基准面是通过起伏地表面得到的,意味着在其对应的速度模型中,从起伏地表面到高速顶界面之间的低降速带区域完成了速度替换,因此在从时间域转换到深度域建模时,可以根据式(9)计算起伏地表面,并在低降速带区域填充替换速度作为近地表模型的速度,时间域分析的均方根速度在转换到深度域后也可以作为中深层的初始速度使用。

而根据平均静校正量法得到的浮动基准面,在满足一定条件时可以通过式(10)或(11)得到对应的起伏地表,在深度域建模时需要根据具体情况在近地表填充背景速度或低降速带速度,时间域解释的均方根速度在转换到深度域后也可以作为中深层的初始速度使用。但如果高速顶界面起伏较大,则不能直接计算对应的起伏地表,在不清楚起伏地表面在空间中的位置时,深度域建模就不能直接使用时间域解释的均方根速度,此时只能在深度域重新进行速度分析和建模。

6 结论

浮动基准面不仅是一个起伏的高程面,还定义了地震道集处理基准面的方式。本文从地震资料处理中常用的浮动基准面的定义出发,讨论了浮动基准面的确定及其物理意义,以及浮动基准面和起伏地表面的关系;提出了将浮动基准面数据用于叠前深度域起伏地表建模和偏移成像的思路,最大限度保留了数据中的t₀时间;指出了根据浮动基准面数据进行深度域建模时容易出现的错误做法及其产生的后果。本次研究为将时间域中的浮动基准面处理和深度域中的起伏地表建模和偏移成像结合在一起提供了有益的参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘治凡

基于浮动基准面的两步法静校正

[J]. 石油物探, 1998,37(1):136-142.

[本文引用: 2]

Liu

Z F

Two step static correction based on floating datum

[J]. GPP, 1998,37(1):136-142.

[本文引用: 2]

[2]

刘治凡, 毛海波, 邵雨, 等.

复杂地表区基准面和静校正方法的选择

[J]. 石油物探, 2003,42(2):240-247.