基于非结构三角网格的海洋CSEM和MT二维联合反演研究

doi:10.11720/wtyht.2021.1384

基于非结构三角网格的海洋CSEM和MT二维联合反演研究

艾正敏^,¹^,², 叶益信¹^,², 汤文武¹^,², 陈晓¹^,², 杜家明¹^,²

1.东华理工大学放射性地质与勘探技术国防重点学科实验室,江西南昌 330013

2.东华理工大学地球物理与测控技术学院,江西南昌 330013

A test study of 2D joint inversion of marine CSEM and MT based on unstructured triangular grid

AI Zheng-Min^,¹^,², YE Yi-Xin¹^,², TANG Wen-Wu¹^,², CHEN Xiao¹^,², DU Jia-Ming¹^,²

1. Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China University of Technology, Nanchang 330013, China

2. School of Geophysics and Measurement and Control Technology, East China University of Technology, Nanchang 330013, China

责任编辑: 沈效群

收稿日期: 2020-07-29 修回日期: 2020-10-25 网络出版日期: 2021-02-20

基金资助:

国家自然科学基金. 41774078
江西省自然科学基金重点项目. 20202ACBL211006

Received: 2020-07-29 Revised: 2020-10-25 Online: 2021-02-20

作者简介 About authors

艾正敏(1995-),男,东华理工大学2018级研究生,主要研究方向为大地电磁法正反演。Email:azm23333@163.com

摘要

采用非结构三角形网格结合快速Occam算法对海洋可控源电磁(CSEM)与大地电磁(MT)数据进行二维联合反演试验研究。非结构三角形网格能够准确地模拟起伏地形和复杂地质构造,对反演目标区域采用精细网格剖分,其他区域采用粗网格剖分,在满足精度的前提下减少了不必要的计算量。将CSEM与MT数据加入到同一反演数据集中,通过对联合反演数据权重公式进行推导,构建CSEM及MT数据相关权重因子,控制不同数据的拟合权重来实现联合反演。最后对不同模型进行了反演计算,结果表明联合反演比单一反演对海底构造与异常体的还原度更高,验证了联合反演算法的可靠性。

关键词： CSEM ; MT ; Occam ; 联合反演 ; 非结构网格

Abstract

In this paper, an unstructured triangular grid combined with a fast Occam algorithm is used to carry out a two-dimensional joint inversion study of marine controlled source electromagnetic (CSEM) and magnetotelluric (MT) data. The unstructured triangular grid can accurately simulate undulating terrain and complex geological structures. Fine meshing is used for the inversion target area, and the other area is divided by coarse meshing, which reduces unnecessary calculations under the premise of meeting accuracy. For the purpose of realizing the joint inversion, the CSEM and MT data are assembled to the same inversion data set, and the relevant weight factors of the CSEM and MT data are constructed from the joint inversion data weight formula, which controls the fitting weights of different data. Finally, inversion calculations are performed on different models, and the results show that the joint inversion has a higher degree of recovery of seafloor structures and anomalous bodies than a single inversion, which verifies the reliability of the joint inversion algorithm.

Keywords： CSEM ; MT ; Occam ; joint inversion ; unstructured grid

PDF (3570KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

艾正敏, 叶益信, 汤文武, 陈晓, 杜家明. 基于非结构三角网格的海洋CSEM和MT二维联合反演研究. 物探与化探[J], 2021, 45(1): 149-158 doi:10.11720/wtyht.2021.1384

AI Zheng-Min, YE Yi-Xin, TANG Wen-Wu, CHEN Xiao, DU Jia-Ming. A test study of 2D joint inversion of marine CSEM and MT based on unstructured triangular grid. Geophysical and Geochemical Exploration[J], 2021, 45(1): 149-158 doi:10.11720/wtyht.2021.1384

0 引言

海洋可控源电磁法(marine controlled-source electromagnetic method, MCSEM)近些年被广泛应用于探测海底油气与研究海洋深部构造等^[1,2,3,4]。海洋电磁法的数值模拟也随之得到了很大的重视,目前大多以二维和三维电磁场的数值模拟为主,而传统的电磁场正演模拟大多使用的是规则网格,一些学者使用非结构三角网格进行了有限元正演模拟^{[5,6,7,8,9,10]},这为非结构三角网格在地球物理电磁场计算中的广泛应用奠定了基础。电磁场的数值模拟通常会产生一些大型的稀疏矩阵,而大规模的反演问题通常是欠定的,这意味着要用有限的参数求取更多的未知数,这也是反演解的非唯一性问题的原因。为了减轻这一问题并提高反演的分辨率,通常利用不同地球物理数据集的互补性质。

在电磁探测方面,CSEM对浅层异常体较为敏感,而MT对深部低阻异常体和大范围电性结构的探测更为有效,二者呈现出互补特性。随着高精度探测的需求,使用CSEM和MT合成数据联合反演的结果进行海底探测成像,将会提高成像结果的分辨率。即使提高了探测精度,反演解的非唯一性问题仍旧存在。有研究者提出在地震和MT联合反演中加入有效的模型约束,使反演的解更实际、更稳定^[11],或者是在地震和MT联合反演中加入有效的岩石物性约束,结合模拟退火模型将电阻率和深度耦合在一起,提高联合反演反演出真实物性参数的可能性^[12]。上述方法考虑的是地震数据和MT数据的联合反演,而关于CSEM和MT数据的联合反演更多的是使用数据加权的方式,通过改变CSEM或MT数据的权重来得到更优的反演结果,提高反演解的分辨率^[13]。随着高精度探测和反演解释的需要,不同方法的联合反演将成为地球物理定量解释的重要工具,是未来地球物理学的一个发展方向^[14,15]。

本文使用合成的CSEM和MT数据进行二维联合反演的模型计算与分析,正演部分采用自适应非结构有限元正演模拟,非结构三角网格能够更好地模拟起伏地形和真实的地质构造,同时能够提高有限元解的精度。反演采用快速Occam算法^[16,17],通过对联合反演数据权重的公式进行推导,构建CSEM与MT数据加权系数,控制不同数据集的权重,提高反演对整体数据的拟合精度,从而得到拟合度更高的反演结果。虽然控制不同数据集的权重可以得到拟合度更高的模型,但这并不意味着拟合度更高的模型就一定和真实模型更接近,因此,本文使用不同的CSEM和MT数据的权重比值来进行联合反演,对不同权重反演得到的结果进行分析与讨论,希望找到最优的权重因子。

1 方法理论

1.1 自适应有限元方法

地球物理电磁场的二维模拟问题通常采用有限单元法(finite element method,FEM)^[18],而应用自适应有限元方法进行电磁场数值模拟,能够自动细化网格并在不显著增加计算时间的条件下提供可靠的计算结果,是一种能够自动调整算法以改进求解过程的数值方法^[5-6,19]。自适应有限元法主要包括偏微分方程求解、误差估计、网格标记和网格优化4个步骤,而其中研究重点是误差估计和自适应网格的优化。本文采用梯度恢复型后验误差估计^[20],即从初始网格出发,通过有限元解的后验误差估计因子来控制后续模型网格的剖分细化。对于某一个有限元网格单元的后验误差估计可表示为:

(1) $\eta_{e}=\left\|(G-I) \nabla u_{h}\right\|_{L_{2}}$

把恢复后的梯度定义为$G \nabla u_{h}$,其中G为梯度恢复算子,u_h为有限元数值解,I是单位算子。

通常来讲,采用局部后验误差估计来评价网格对数值结果的影响,并对误差较大的单元进行局部细化的技术,能够得到较高精度数值解。但是,有限元方程的解依赖于整个区域的资料,如果限制在局部区域,则会带来一些多余的网格细化,增加计算量。对偶误差估计加权方法(dual error weighting,DEW)^[5-6,21]能够在全局区域分析网格单元对有限元的数值解精度的影响,从而能有效解决上述问题,同时引入一个超收敛梯度恢复算子G=SⁿQ_h,运用DEW方法加权后的 ${\dot{η}}_{e}$ 可表示为

(2)$\hat{\eta}_{e}=\left\|(G-I) \nabla u_{h}\right\|_{L_{2}} \cdot\left\|k(G-I) \nabla \omega_{h}\right\|_{L_{2}}=\left\|\left(S^{n} Q_{h}-I\right) \nabla u_{h}\right\|_{L_{2}} \cdot\left\|k\left(S^{n} Q_{h}-I\right) \nabla \omega_{h}\right\|_{L_{2}}$

式中:Q_h是L₂投影算子;S是平滑算子;n为平滑迭代次数;k表示模型参数的约束;$ \nabla \omega_{h}$为对偶问题有限元解的梯度。

1.2 反演算法

本文海洋CSEM与MT数据联合反演方法采用的是快速Occam算法^[16,17],该算法实质为带光滑约束的最小二乘法,其泛函U表达式为:

(3)

U = μ (P ‖ m - m_{*} ‖^{2} + ‖ Rm ‖^{2}) + ‖ W (d - F (m)) ‖^{2}

式中:m为N维的模型参数矢量,一般为电阻率值;P为正则项对应的权重系数矩阵;R为粗糙度算子矩阵;μ为拉格朗日乘子,用以平衡模型粗糙度和数据拟合误差,当μ取较大值时,反演以搜索光滑模型为主,反之则以搜索最小拟合误差为主;W为关联的对角加权矩阵;d为观测数据矢量;F(m)为模型m对应的正演响应。

关于给定初始模型m_k的函数,通过以下迭代方法实现目标函数的最小化:

(4)

m_{k + 1} = [μ (R^{T} R + P^{T} P + (W J_{k})^{T} W J_{k}]^{- 1} \times [(W J_{k})^{T} W \dot{d} + μ P^{T} P m_{k}]

式中: $\dot{d}$ =d-F(m_k)+J_km_k;雅可比矩阵J为M×N大小的矩阵,其中每个分量的表达式为:

(5)

J_{ij} = \frac{\partial F_{i} [m]}{\partial m_{j}}

通过上述模型迭代计算公式,将上一次的计算结果作为下一次计算的初始模型,μ在第一次迭代中给出初始值,之后每次迭代都按照线性搜索方式计算得出。如果这种迭代算法最后收敛,那就得到了目标函数U最小化的解,并且与初始模型m_k不相关,最后的结果将是在满足数据拟合误差前提下最平缓的模型。

1.3 联合反演数据权重

MT和CSEM数据的联合反演可以改进海洋勘探的结构成像^[13,22]。通过联合反演弥补单独反演勘探深度或勘探精度的不足,进而得到比单独反演效果更好的结果。然而,联合反演存在的一个问题是当每个子集的数据量存在很大差异时,怎么样才能相同地拟合每个数据子集。本文通过对不同子集拟合误差的加权来控制联合反演的权重,从而得到更好的反演效果。例如,将一个n维数据划分为具有维度n₁和n₂的MT和CSEM子集,对于n维数据向量d,有:

(6)

d = [d_{1} d_{2}]^{T}

然后可以将目标函数中的误差函数扩展为:

(7)

‖ W (d - F (m)) ‖^{2} = ‖ W_{1} (d_{1} - F_{1} (m)) ‖^{2} + ‖ W_{2} (d_{2} - F_{2} (m)) ‖^{2}

(8)

χ^{2} = χ_{1}^{2} + χ_{2}^{2}

当拟合误差达到或十分接近设定的目标拟合差的时候,可以认为这是一个很好的模型。理想情况下,联合反演应该产生1个同样拟合2个数据子集的模型,即 $χ_{1}^{2}$ ≈n₁, $χ_{2}^{2}$ ≈n₂。由于2个数据集大小不同且不能单一对某一数据集进行拟合而忽略了另一个数据集。因此假定通过增加数据权重系数α₁、α₂以达到预期误差,α₁、α₂的取值与每个子集的数据量有关。使用加权的联合反演数据集的误差函数可满足以下关系:

(9)

‖ α_{1} W_{1} (d_{1} - F_{1} (m)) ‖^{2} + ‖ α_{2} W_{2} (d_{2} - F_{2} (m)) ‖^{2} = \frac{χ_{1}^{2}}{n_{1}} + \frac{χ_{2}^{2}}{n_{2}}

式中:α_i= $\sqrt[]{k_{i} / n_{i}}$ ,是数据平衡权重,它对每个误差函数进行标准化,以便较小的数据子集对总体误差的影响与较大的子集一样大。通常情况下会令k_i=1,则同样拟合这两个子集的模型可以表示为

(10)

\frac{χ_{1}^{2}}{n_{1}} + \frac{χ_{2}^{2}}{n_{2}} \approx 1 + 1

这种方法与前人对联合MT和CSEM反演有效的加权公式基本相同^[13]。在该方法中,可以通过指定α₁=1和α₂= $\sqrt[]{n_{1} / n_{2}}$ 将加权仅用于d₂。

根据上面的公式,可以进一步扩展到N个子集的情况。具有N个子集的数据向量可以表示为:

(11)

d = [d_{1} d_{2} \dots d_{N}]^{T}

这种情况下的误差函数或者说是拟合差的均方根值(RMS)的平方可以表示为:

(12)

{(RMS)}^{2} = ‖ W (d - F (m)) ‖^{2} = \overset{N}{\sum_{i = 1}} ‖ α_{i} W_{i} (d_{i} - F_{i} (m) ‖^{2}

虽然CSEM与MT子集的数据量和数据类型是不一样的,CSEM子集包含电磁场的振幅和相位,MT子集包含TE、TM模式的视电阻率和相位,但是这种方法对将CSEM和MT数据集放入一个数据集中进行反演仍将是有用的,同时,该方法也可用于大地电磁测深数据和地震数据的联合反演^[23,24]。

1.4 联合反演流程

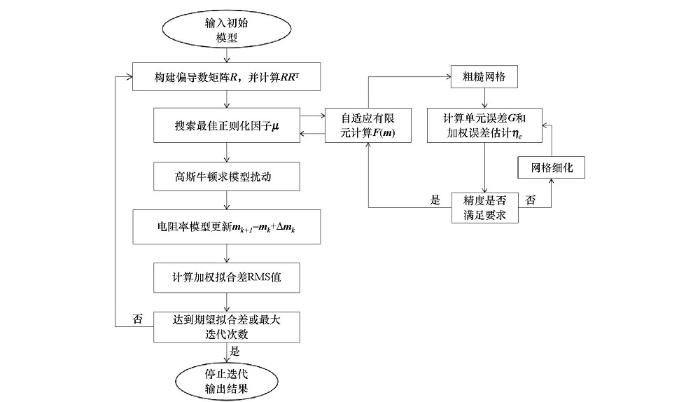
本文采用的海洋可控源电磁和大地电磁数据联合反演计算流程见图1。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 联合反演流程示意

Fig.1 Schematic diagram of the joint inversion process

2 模型计算

2.1 简单模型反演计算

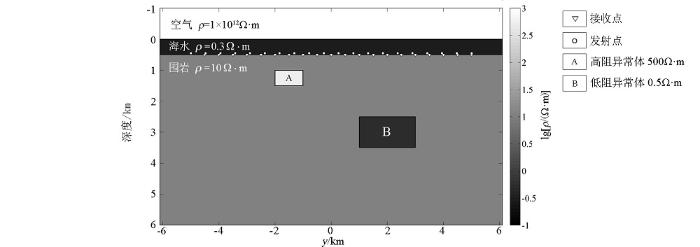
为验证反演算法的可靠性,本文设置了一个二维水平海底模型并进行反演计算。模型如图2所示,在海水层厚为500 m的海底设置了两个异常体,浅部异常体A的电阻率为500 Ω·m,大小为1 000 m×500 m,深部异常体B的电阻率为0.5 Ω·m,大小为2 000 m×1 000 m。MT与CSEM采用相同的接收点,从左往右依次设置了20个测点,间距500 m,MT的频率范围为0.001~1 Hz,取对数等间隔分布选取了20个频点。CSEM发射源均匀分布在-5 000~5 000 m范围内,共20个,位于海底上方50 m的海水中,发射源频率分别为1 Hz、5 Hz。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 二维水平海底模型

Fig.2 Two-dimensional model with flat seafloor

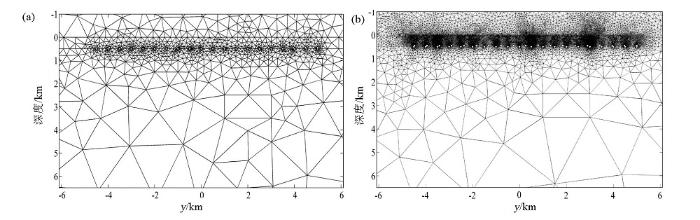
针对上述模型分别进行CSEM与MT正演,网格采用算法中的自适应网格剖分。以CSEM正演网格为例,如图3所示,模型正演计算的初次细化后的网格剖分为由1 445个节点形成的2 849个三角单元,第12次细化后的最终网格剖分为由43 127个节点形成的86 139个三角单元。可以看出,由于测点附近的网格剖分对测点接收到的电磁场分量影响较大,所以在自适应网格优化过程中,对浅地表和测点附近的网格进行了加密,而边界和深部的网格并没有进行加密。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 自适应正演网格剖分示意(以CSEM网格为例)

a—初次优化网格,1 445个节点,2 849个三角单元; b—第12次自适应细化后的最终网格部分,43 127个节点,86 139个三角单元; 示意图只展示了模型中间的异常区域

Fig.3 Schematic diagram of adaptive forward meshing (taking CSEM mesh as an example)

a—the first optimized mesh containing 1 445 nodes and 2 849 triangular elements; b—the final mesh after the 12th adaptive refinement, containing 43 127 nodes and 86 139 triangular elements; the diagram only shows the abnormal area in the middle part of the model

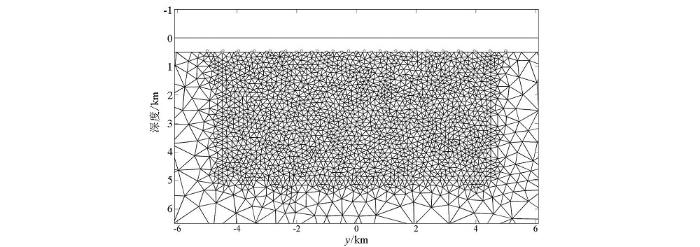
对模型进行有限元正演计算,CSEM正演得到的是E_y的幅值和相位的响应值,MT正演得到的是TE、TM模式的视电阻率和相位的响应值,对得到的响应值添加4%的随机高斯噪声,则生成了反演计算所需的观测数据。反演的初始模型包含空气、海水和海底地层,其中空气和海水电阻率不参与反演,给定地层的初始电阻率为1.0 Ω·m。计算区域所划分的单元越多,所需要的计算量越大,因此只对目标反演区域采用较细的网格剖分,其余部分则采用粗网格以减少不必要的计算量。如图4所示,选取y范围为-4.5~4.5 km海底到5 km深的区域,调用Triangle程序^[25]对该区域进行精细网格剖分,共生成3 756个三角单元,其余部分共剖分为440个三角形单元。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 初始模型的反演网格剖分

Fig.4 Inversion mesh division of the initial model

设定目标均方根误差为1.0,输入初始模型,调用程序对模型数据进行反演计算。在个人电脑上,MT数据单独反演经过20次迭代得到图5a所示结果,CSEM数据单独反演经过15次迭代得到图5b所示结果,CSEM与MT数据联合反演经过21次迭代最终得到图5c所示结果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

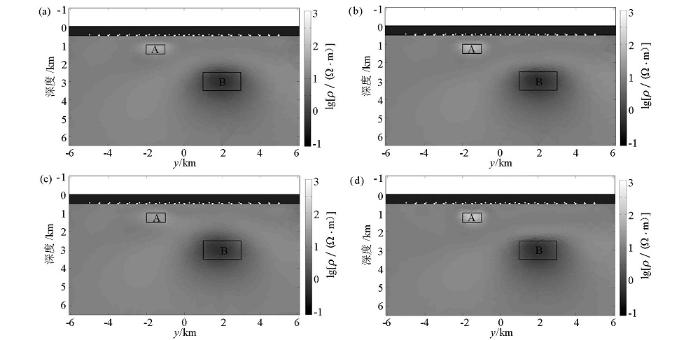
图5 简单模型反演结果

a—MT反演; b—CSEM反演; c—CSEM与MT联合反演

Fig.5 Inversion results of the simple two-dimensional model

a—MT data inversion result; b—CSEM data inversion result; c—CSEM+MT data joint inversion result

对比3个反演的结果可以看出,MT对深部异常体的反演效果较好,对浅部异常体无法进行识别,CSEM对浅部的反演效果非常好,对深部的反演则存在一些偏差,对浅部异常体边界和埋深的反映与模型基本一致。整体来看,联合反演对浅部和深部的反演效果都很不错,但浅部的反演出的电阻率没有CSEM反演出的视电阻率更接近模型的真电阻率,尽管如此,联合反演在效果上依旧比MT或CSEM反演更具有优势。

图6为联合反演得到的最终模型MT响应与MT观测数据的拟断面对比,图7为发射源在y=0处CSEM观测数据与联合反演的CSEM模型响应的振幅和相位拟合结果。可以看出,模拟数据与真实数据的视电阻率和相位信息高度吻合,验证了反演结果的可靠性和准确度,说明本文采用的联合反演方法能有效识别不同深度的异常体。

图6

新窗口打开| 下载原图ZIP| 生成PPT

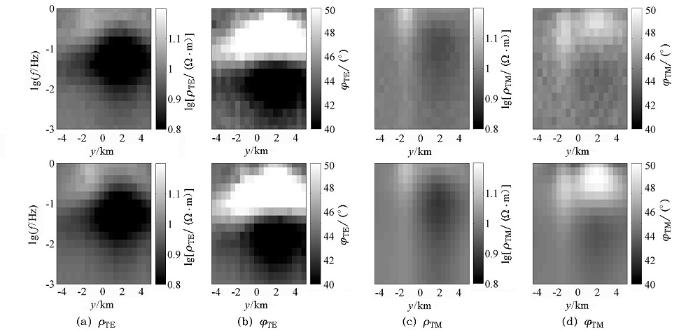
图6 MT观测数据(上)与联合反演正演响应(下)的拟断面图对比

Fig.6 Comparison of pseudo-section diagrams of MT observation data (top) and MT forward responses of joint inversion model (bottom)

图7

新窗口打开| 下载原图ZIP| 生成PPT

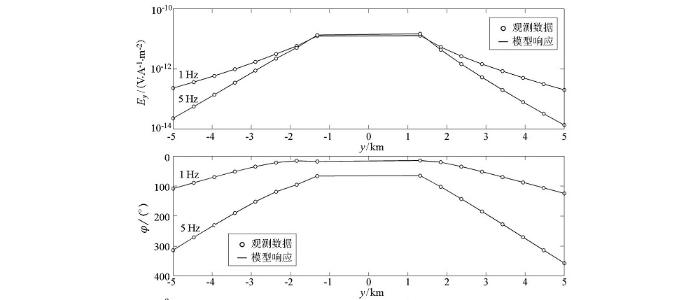
图7 发射源在y=0处CSEM观测数据与联合反演模型响应的振幅和相位拟合

Fig.7 Amplitude and phase fitting diagram of the CSEM observation data and model response of the joint inversion result with the emission source at y=0

表1给出了上述3种方法反演的最终耗时、均方根拟合差RMS及粗糙度。从表中可以看出,MT的反演耗时为157.7 min,CSEM的反演耗时为368.5 min,联合反演的耗时为1 247.3 min,联合反演时数据量增加了一倍,导致反演时间大大增加,在以后的研究中应该考虑对联合反演数据集的选取研究和进行算法的优化。

表1 反演耗时、拟合差、粗糙度及迭代次数统计

Table 1 List of time-consuming, RMS misfit, roughness and iteration number of inversion

方法	数据个数	耗时/min	拟合差RMS	粗糙度	迭代次数
MT	1280	157.7	2.7435	9.4157	20
CSEM	1226	368.5	1.0099	13.76	15
CSEM+MT	2506	1247.3	2.8047	13.02	21

新窗口打开| 下载CSV

2.2 简单模型不同权重联合反演计算

假设权重因子q=α_MT/α_CSEM=α₁/α₂,图2模型联合反演中使用的权重因子为1,使用权重因子为1的好处是可以在CSEM和MT数据量相差不大时更好地拟合2个数据子集,但并不是在所有的情况下都选择1为权重因子的。在一些数据量差异较大时,就需要找到最优的权重因子并用于联合反演。因此,本文使用不同的权重因子对图2中的模型再次进行联合反演。

图8是使用不同权重因子的联合反演结果示意,可以看出:q值越小,即CSEM数据权重系数越大时,联合反演对浅部高阻异常体探测效果更好,而当q值越大,即MT数据权重系数更大时,联合反演对浅部异常体的探测能力变弱了,对深部异常体的探测效果并没有很大改变。所以,可认为权重因子q对联合反演中的CSEM数据影响更大。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同权重因子q值时的联合反演结果

Fig.8 Joint inversion results with different q value

a—q=2;b—q=0.5;c—q=10;d—q=0.1

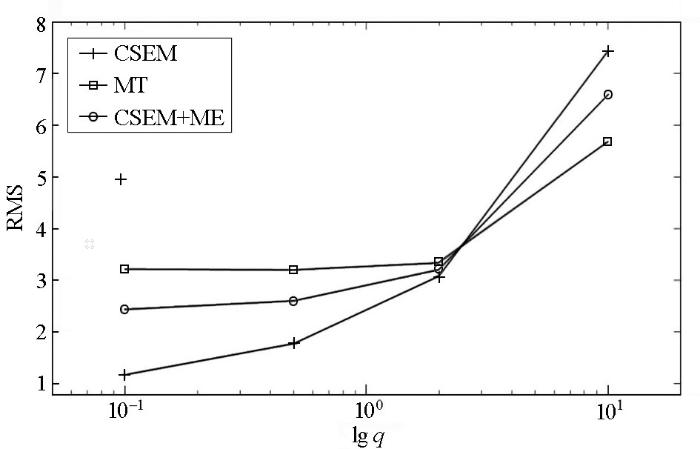
图9为不同q值时联合反演最终所得模型的RMS值,可以看出,权重因子q=0.1时的拟合差要明显低于q=10的拟合差,而且联合反演对MT数据的拟合差并没有随着q值的变大而变小,反而是随着q值的变大而变大,这也是因为MT权重太大导致的,在联合反演时需要充分拟合2个数据集,而不是过于偏向某个数据集。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同q值时联合反演最终RMS值

Fig.9 The final RMS value of joint inversion with different q value

2.3 复杂模型反演计算

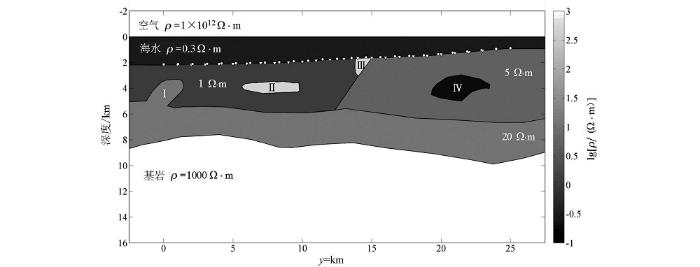
为进一步验证反演算法的准确性和可靠性,设计了1个海底二维带地形的复杂模型。如图10所示,海水电阻率为0.3 Ω·m,海底下方设置了4个异常体,Ⅰ号异常体是一个中间层的侵入体,电阻率为20 Ω·m;Ⅱ号与Ⅳ号异常体在2个不同的地层中,电阻率分别为500 Ω·m和0.2 Ω·m;Ⅲ号异常体位于地层浅部,电阻率为500 Ω·m。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 二维复杂海洋模型

Fig.10 Two-dimensional complex ocean model

在海底设置了25个观测装置(图10中白色三角符号所示),测点在1~25 km范围沿海底地形均匀的分布。MT和CSEM的接收点位置相同,CSEM发射源位于海底上方50 m的海水中,范围在0~25 km内均匀分布共25个。MT观测频率范围为10^-4~0.1 Hz,取对数等间隔分布,共20个,CSEM发射频率分别为0.1、1、10 Hz。对该模型进行有限元正演计算,得到其视电阻率、振幅和相位响应值,对响应值添加4%高斯随机噪声,得到反演所需的观测数据。反演初始模型包括空气、海水和海底地层,其中空气和海水电阻率为固定值不参与反演,给定地层的初始电阻率为1.0 Ω·m。

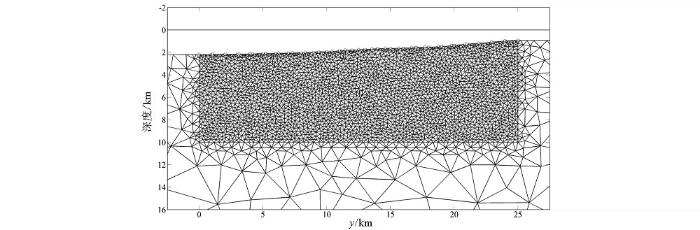
对初始模型进行剖分,如图11所示,根据接收点和发射点的位置分布对异常体或构造可能存在的区域进行精细网格剖分,其余部分则采用不加约束的粗网格剖分。精细网格的剖分可以保证计算的精度,采用粗网格则可以减少不必要的计算量。调用Triangle程序^[25]对反演区域剖分,最终剖分得到 6 089 个三角单元。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 初始模型的反演网格剖分

Fig.11 Inversion mesh division of the initial model

设定目标均方根误差为1.0,输入初始模型。MT观测数据2 000个,CSEM观测数据1 842个,总的观测数据为3 842个,其中数据量比值N_CSEM/N_MT=0.921,对于MT与CSEM数据量比值接近1的情况,采用权重因子q=1,以便联合反演能够同等拟合2个观测数据集,提高反演的分辨率。反演结果见图12。

图12

新窗口打开| 下载原图ZIP| 生成PPT

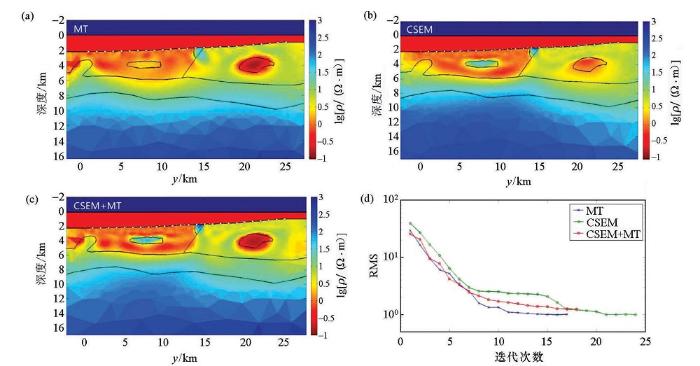
图12 反演结果

a—MT反演; b—CSEM反演; c—CSEM与MT联合反演; d—误差变化

Fig.12 Inversion result

a—MT data inversion result; b—CSEM data inversion result; c—CSEM+MT data joint inversion result; d—RMS diagram

图12a是MT数据经迭代17次的反演结果,图12b是CSEM数据迭代24次反演结果,图12c是CSEM+MT数据经迭代18次的联合反演结果。整体来看,MT反演能够恢复较大的低阻异常体电阻率,但不能恢复较小和较大的高阻异常体,虽然能够识别深部基岩,但基岩起伏面不够明显。CSEM反演结果对浅部高阻异常体和深部基岩电阻率的恢复比MT好一点,同时更好区分浅部的两个不同地层,但对低阻异常体的电阻率和几何形态恢复得较差。相对前两种反演方法,联合反演对异常体的位置反演得十分准确,也没有产生过多虚假异常,对浅部地层分界面能够进行较好的区分,同时基岩起伏界面也比较明确,与真实模型十分接近,这也说明该算法可用于复杂模型的联合反演,进一步证明了该算法的有效性。图12d为反演过程中RMS随迭代次数的变化曲线,如图所示,反演经过多次迭代,最终RMS都下降到1左右。

3 结论

本文探讨和分析了基于非结构三角网格的海洋CSEM和MT数据的联合反演。从目标函数出发,采用数据加权的方式以达到对CSEM和MT数据子集的迭代拟合;然后对模型进行了正反演试算,发现联合反演的效果比单一反演效果更好。联合反演结合了CSEM与MT方法的各自优势,使用不同的权重因子q进行联合反演,能够有效识别不同深度的异常体与构造,且对地层电阻率恢复度较高,与真实模型更加接近,同时,反演生成模型的正演响应与观测数据非常吻合,反演迭代收敛稳定,结果真实可靠,证明了本文算法的有效性。

本文在数据加权上只是单纯地对不同数据集进行加权,并没有得到加权系数与探测深度和探测精度之间的关系,而且联合反演的耗时较大,因此需要进行联合反演数据集的选取和算法优化研究。目前尚缺少实测数据的联合反演实例。对于后续实测数据的联合反演过程,建议首先需要了解不同方法数据的探测深度和分辨率,通过几次单独的反演尝试了解,然后使用适当的数据权重对合成的CSEM和MT数据进行联合反演,数据权重可以根据数据量的比值适当选取。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Constable

, Srnka

L J

An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration

[J]. Geophysics, 2007,72(2):3-12.

[本文引用: 1]

[2]

Constable

Ten years of marine CSEM for hydrocarbon exploration

[J]. Geophysics, 2010,75(5):67-81.

[本文引用: 1]

[3]

汪海峰, 邓明, 陈凯.

海底电磁接收机新进展

[J]. 物探与化探, 2016,40(4):809-815.

DOI:10.11720/wtyht.2016.4.27 URL [本文引用: 1]

Hz@0.5 Hz，动态范围大于110 dB，时漂小于5 ms/day，与国外同类先进产品技术指标平齐。截止到2016年初，累计完成了约60站位的海底电磁数据采集作业，2012年以来接收机回收率达到100%，获取了多批次高质量的海底MT及CSEM资料，研制的接收机成功应用于水合物勘查及油气勘探领域。]]>

Wang

H F

, Deng

, Chen

New progress of submarine electromagnetic receivers

[J]. Geophysical and Geochemical Exploration, 2016,40(4):809-815.

[本文引用: 1]

[4]

陈凯, 景建恩, 赵庆献, 等.

海底可控源电磁接收机及其水合物勘查应用

[J]. 地球物理学报, 2017,60(11):4262-4272.

[本文引用: 1]

Chen

, Jing

J E

, Zhao

Q X

, et al.

Submarine controllable source electromagnetic receiver and its application in hydrate exploration

[J]. Chinese Journal of Geophysics, 2017,60(11):4262-4272.

[本文引用: 1]

[5]

Key

, Weiss

Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example

[J]. Geophysics, 2006,71(6):G291-G299.

DOI:10.1190/1.2348091 URL [本文引用: 3]

[6]

Y G

, Key

2D marine controlled-source electromagnetic modeling:Part 1—An adaptive finite-element algorithm

[J]. Geophysics, 2007,72(2):WA51-WA62.

[本文引用: 3]

[7]

Key

, Ovall

J S

A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling

[J]. Geophysical Journal International, 2011,186(1):137-154.

DOI:10.1111/j.1365-246X.2011.05025.x URL [本文引用: 1]

We present a parallel goal-oriented adaptive finite element method that can be used to rapidly compute highly accurate solutions for 2.5-D controlled-source electromagnetic (CSEM) and 2-D magnetotelluric (MT) modelling problems. We employ unstructured triangular grids that permit efficient discretization of complex modelling domains such as those containing topography, dipping layers and multiple scale structures. Iterative mesh refinement is guided by a goal-oriented error estimator that considers the relative error in the strike aligned fields and their spatial gradients, resulting in a more efficient mesh refinement than possible with a previous approach based on the absolute errors. Reliable error estimation is accomplished by a dual weighted residual method that is carried out via hierarchical basis computations. Our algorithm is parallelized over frequencies, wavenumbers, transmitters and receivers, where adaptive refinement is performed in parallel on subsets of these parameters. Mesh sharing allows an adapted mesh generated for a particular frequency and wavenumber to be shared with nearby frequencies and wavenumbers, thereby efficiently reducing the parallel load of the adaptive refinement calculations. We demonstrate the performance of our algorithm on a large cluster computer through scaling tests for a complex model that includes strong seafloor topography variations and multiple thin stacked hydrocarbon reservoirs. In tests using up to 800 processors and a realistic suite of CSEM data parameters, our algorithm obtained run-times as short as a few seconds to tens of seconds.

[8]

韩波, 胡祥云, 黄一凡, 等.

基于并行化直接解法的频率域可控源电磁三维正演

[J]. 地球物理学报, 2015,58(8):2812-2826.

[本文引用: 1]

Han

, Hu

X Y

, Huang

Y F

, et al.

3D frequency domain CSEM modeling using a parallel direct solver

[J]. Chinese Journal of Geophysics, 2015,58(8):2812-2826.

[本文引用: 1]

[9]

韩骑, 胡祥云, 程正璞, 等.

自适应非结构有限元MT二维起伏地形正反演研究

[J]. 地球物理学报, 2015,58(12):4675-4684.

[本文引用: 1]

Han

, Hu

X Y

, Chen

Z P

, et al.

A study of two dimensional MT inversion with steep topography using the adaptive unstructured finite element method

[J]. Chinese Journal of Geophysics, 2015,58(12):4675-4684.

[本文引用: 1]

[10]

叶益信, 李予国, 刘颖, 等.

基于局部加密非结构网格的海洋可控源电磁法三维有限元正演

[J]. 地球物理学报, 2016,59(12):4747-4758.

[本文引用: 1]

Y X

, Li

Y G

, Liu

, et al.

3D finite element modeling of marine controlled source electromagnetic fields using locally refined unstructured meshes

[J]. Chinese Journal of Geophysics, 2016,59(12):4747-4758.

[本文引用: 1]

[11]

陈晓, 于鹏, 张罗磊, 等.

大地电磁与地震正则化同步联合反演

[J]. 地震地质, 2010,32(3):402-408.

DOI:10.3969/j.issn.0253－4967.2010.03.006 URL [本文引用: 1]

文中在于鹏等提出的电阻率和速度随机分布的大地电磁与地震联合反演方法的基础上,将Tikhonov正则化思想引入到联合反演中,加入先验信息进行模型约束,以最小模型为稳定器,采用L曲线方法来确定近似最佳的正则化因子。考虑到线性寻优算法容易陷入局部极小,文中采用非线性的模拟退火方法来实现大地电磁与地震的同步联合反演。通过模型试验的对比分析,我们认为加入有效模型约束的正则化联合反演可以比单纯考虑数据拟合的联合反演和单独反演方法更有效地提高解的稳定性和计算效率,获得更接近实际而且稳定的解。

Chen

, Yu

, Zhang

L L

, et al.

Synchronous joint inversion of magnetotelluric and seismic regularization

[J]. Seismology and Geology, 2010,32(3):402-408.

[本文引用: 1]

[12]

陈晓, 于鹏, 邓居智, 等.

基于宽范围岩石物性约束的大地电磁和地震联合反演

[J]. 地球物理学报, 2016,59(12):4690-4700.

[本文引用: 1]

Chen

, Yu

, Deng

J Z

, et al.

Joint inversion of magnetotelluric and seismic based on wide range of rock property constraints

[J]. Chinese Journal of Geophysics, 2016,59(12):4690-4700.

[本文引用: 1]

[13]

Commer

, Newman

G A

Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion

[J]. Geophysical Journal International, 2009,178(3):1305-1316.

DOI:10.1111/gji.2009.178.issue-3 URL [本文引用: 3]

[14]

Sasaki

3D inversion of marine CSEM and MT data: An approach to shallow-water problem

[J]. Geophysics, 2013,78(1):59-65.

[本文引用: 1]

[15]

Blatter

, Key

, Ray

, et al.

Bayesian joint inversion of controlled source electromagnetic and magnetotelluric data to image freshwater aquifer offshore New Jersey

[J]. Geophysical Journal International, 2019,218(3):1822-1837.

DOI:10.1093/gji/ggz253 URL [本文引用: 1]

[16]

Constable

S C

, Parker

R L

, Constable

C G

Occam’s inversion-a practical algorithm for generating smooth models from electromagnetic sounding data

[J]. Geophysics, 1987,52(3):289-300.

DOI:10.1190/1.1442303 URL [本文引用: 2]

[17]

Key

MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data

[J]. Geophysical Journal International, 2016,207(1):571-588.

DOI:10.1093/gji/ggw290 URL [本文引用: 2]

[18]

徐世浙

. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994: 159-170.

[本文引用: 1]

S Z

. The finite element method in geophysics[M]. Beijing: Science Press, 1994: 159-170.

[本文引用: 1]

[19]

Franke

, Borner

, Spitzer

, et al.

Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography

[J]. Geophysical Journal International, 2007,171(1):71-86.

DOI:10.1111/gji.2007.171.issue-1 URL [本文引用: 1]

[20]

Bank

R E

, Xu

J C

Asymptotically exact a posteriori error estimators, Part Ⅱ: General unstructured grids

[J]. SIAM Journal on Numerical Analysis, 2003,41:2313-2332.

DOI:10.1137/S0036142901398751 URL [本文引用: 1]

[21]

Ovall

J S

Asymptotically exact functional error estimators based on superconvergent gradient recovery

[J]. Numerical Mathematics, 2006,102:543-558.

DOI:10.1007/s00211-005-0655-9 URL [本文引用: 1]

[22]

Wiik

, Hokstad

, Ursin

, et al.

Joint contrast source inversion of marine magnetotelluric and controlled-source electromagnetic data

[J]. Geophysics, 2013,78(6):315-327.

[本文引用: 1]

[23]

Bennington

N L

, Zhang

, Thurber

C H

, et al.

Joint inversion of seismic and magnetotelluric data in the Parkfield Region of California using the normalized cross-gradient constraint

[J]. Pure and Applied Geophysics, 2015,172(5):1033-1052.

DOI:10.1007/s00024-014-1002-9 URL [本文引用: 1]

[24]

熊彬, 罗天涯, 蔡红柱, 等.

起伏地形大地电磁二维反演

[J]. 物探与化探, 2016,40(3):587-593.

DOI:10.11720/wtyht.2016.3.22 URL [本文引用: 1]

为了适应地形起伏的实际地质情况,开展带地形的最小二乘二维反演研究。鉴于大地电磁(MT)反演的不适定问题,引入Tikhonov的正则化方法,从而获得关于总目标函数的方程,利用光滑约束最小二乘法求解总目标函数方程。由于正则化因子值与反演精度以及稳定性相关,采用主动约束平衡方法获取最优化的正则化因子,以确保反演精度和稳定性都达到最佳。与此同时,利用电磁场互易定理以节省反演迭代过程求解雅可比矩阵的计算时间。构建了若干地质构造模型进行试算,分别讨论TE、TM模式以及二者联合模式的反演结果,并与前人研究工作对比以说明本文方法的反演效果。

Xiong

, Luo

T Y

, Cai

H Z

, et al.

Two-dimensional magnetotelluric inversion of undulating terrain

[J]. Geophysical and Geochemical Exploration, 2016,40(3):587-593.

[本文引用: 1]

[25]

Shewchuk

J R

Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator

[C]// Workshop on Applied Computational Geometry. Springer, Berlin, Heidelberg, 1996: 203-222.

[本文引用: 2]

An introduction to marine controlled-source electromagnetic methods for hydrocarbon exploration

2007

... 海洋可控源电磁法(marine controlled-source electromagnetic method, MCSEM)近些年被广泛应用于探测海底油气与研究海洋深部构造等^[1,2,3,4].海洋电磁法的数值模拟也随之得到了很大的重视,目前大多以二维和三维电磁场的数值模拟为主,而传统的电磁场正演模拟大多使用的是规则网格,一些学者使用非结构三角网格进行了有限元正演模拟^{[5,6,7,8,9,10]},这为非结构三角网格在地球物理电磁场计算中的广泛应用奠定了基础.电磁场的数值模拟通常会产生一些大型的稀疏矩阵,而大规模的反演问题通常是欠定的,这意味着要用有限的参数求取更多的未知数,这也是反演解的非唯一性问题的原因.为了减轻这一问题并提高反演的分辨率,通常利用不同地球物理数据集的互补性质. ...

Ten years of marine CSEM for hydrocarbon exploration

2010

海底电磁接收机新进展

2016

海底电磁接收机新进展

2016

海底可控源电磁接收机及其水合物勘查应用

2017

海底可控源电磁接收机及其水合物勘查应用

2017

Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example

2006

... 地球物理电磁场的二维模拟问题通常采用有限单元法(finite element method,FEM)^[18],而应用自适应有限元方法进行电磁场数值模拟,能够自动细化网格并在不显著增加计算时间的条件下提供可靠的计算结果,是一种能够自动调整算法以改进求解过程的数值方法^[5-6,19].自适应有限元法主要包括偏微分方程求解、误差估计、网格标记和网格优化4个步骤,而其中研究重点是误差估计和自适应网格的优化.本文采用梯度恢复型后验误差估计^[20],即从初始网格出发,通过有限元解的后验误差估计因子来控制后续模型网格的剖分细化.对于某一个有限元网格单元的后验误差估计可表示为: ...

... 通常来讲,采用局部后验误差估计来评价网格对数值结果的影响,并对误差较大的单元进行局部细化的技术,能够得到较高精度数值解.但是,有限元方程的解依赖于整个区域的资料,如果限制在局部区域,则会带来一些多余的网格细化,增加计算量.对偶误差估计加权方法(dual error weighting,DEW)^[5-6,21]能够在全局区域分析网格单元对有限元的数值解精度的影响,从而能有效解决上述问题,同时引入一个超收敛梯度恢复算子G=SⁿQ_h,运用DEW方法加权后的

{\dot{η}}_{e}

可表示为 ...

2D marine controlled-source electromagnetic modeling:Part 1—An adaptive finite-element algorithm

2007

{\dot{η}}_{e}

可表示为 ...

A parallel goal-oriented adaptive finite element method for 2.5-D electromagnetic modelling

2011

基于并行化直接解法的频率域可控源电磁三维正演

2015

基于并行化直接解法的频率域可控源电磁三维正演

2015

自适应非结构有限元MT二维起伏地形正反演研究

2015

自适应非结构有限元MT二维起伏地形正反演研究

2015

基于局部加密非结构网格的海洋可控源电磁法三维有限元正演

2016

基于局部加密非结构网格的海洋可控源电磁法三维有限元正演

2016

大地电磁与地震正则化同步联合反演

2010

... 在电磁探测方面,CSEM对浅层异常体较为敏感,而MT对深部低阻异常体和大范围电性结构的探测更为有效,二者呈现出互补特性.随着高精度探测的需求,使用CSEM和MT合成数据联合反演的结果进行海底探测成像,将会提高成像结果的分辨率.即使提高了探测精度,反演解的非唯一性问题仍旧存在.有研究者提出在地震和MT联合反演中加入有效的模型约束,使反演的解更实际、更稳定^[11],或者是在地震和MT联合反演中加入有效的岩石物性约束,结合模拟退火模型将电阻率和深度耦合在一起,提高联合反演反演出真实物性参数的可能性^[12].上述方法考虑的是地震数据和MT数据的联合反演,而关于CSEM和MT数据的联合反演更多的是使用数据加权的方式,通过改变CSEM或MT数据的权重来得到更优的反演结果,提高反演解的分辨率^[13].随着高精度探测和反演解释的需要,不同方法的联合反演将成为地球物理定量解释的重要工具,是未来地球物理学的一个发展方向^[14,15]. ...

大地电磁与地震正则化同步联合反演

2010

基于宽范围岩石物性约束的大地电磁和地震联合反演

2016

基于宽范围岩石物性约束的大地电磁和地震联合反演

2016

Three-dimensional controlled-source electromagnetic and magnetotelluric joint inversion

2009

... MT和CSEM数据的联合反演可以改进海洋勘探的结构成像^[13,22].通过联合反演弥补单独反演勘探深度或勘探精度的不足,进而得到比单独反演效果更好的结果.然而,联合反演存在的一个问题是当每个子集的数据量存在很大差异时,怎么样才能相同地拟合每个数据子集.本文通过对不同子集拟合误差的加权来控制联合反演的权重,从而得到更好的反演效果.例如,将一个n维数据划分为具有维度n₁和n₂的MT和CSEM子集,对于n维数据向量d,有: ...

... 这种方法与前人对联合MT和CSEM反演有效的加权公式基本相同^[13].在该方法中,可以通过指定α₁=1和α₂=

\sqrt[]{n_{1} / n_{2}}

将加权仅用于d₂. ...

3D inversion of marine CSEM and MT data: An approach to shallow-water problem

2013

Bayesian joint inversion of controlled source electromagnetic and magnetotelluric data to image freshwater aquifer offshore New Jersey

2019

Occam’s inversion-a practical algorithm for generating smooth models from electromagnetic sounding data

1987

... 本文使用合成的CSEM和MT数据进行二维联合反演的模型计算与分析,正演部分采用自适应非结构有限元正演模拟,非结构三角网格能够更好地模拟起伏地形和真实的地质构造,同时能够提高有限元解的精度.反演采用快速Occam算法^[16,17],通过对联合反演数据权重的公式进行推导,构建CSEM与MT数据加权系数,控制不同数据集的权重,提高反演对整体数据的拟合精度,从而得到拟合度更高的反演结果.虽然控制不同数据集的权重可以得到拟合度更高的模型,但这并不意味着拟合度更高的模型就一定和真实模型更接近,因此,本文使用不同的CSEM和MT数据的权重比值来进行联合反演,对不同权重反演得到的结果进行分析与讨论,希望找到最优的权重因子. ...

... 本文海洋CSEM与MT数据联合反演方法采用的是快速Occam算法^[16,17],该算法实质为带光滑约束的最小二乘法,其泛函U表达式为: ...

MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data

2016

... 本文海洋CSEM与MT数据联合反演方法采用的是快速Occam算法^[16,17],该算法实质为带光滑约束的最小二乘法,其泛函U表达式为: ...

1994

Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography

2007

Asymptotically exact a posteriori error estimators, Part Ⅱ: General unstructured grids

2003

Asymptotically exact functional error estimators based on superconvergent gradient recovery

2006

{\dot{η}}_{e}

可表示为 ...

Joint contrast source inversion of marine magnetotelluric and controlled-source electromagnetic data

2013

Joint inversion of seismic and magnetotelluric data in the Parkfield Region of California using the normalized cross-gradient constraint

2015

... 虽然CSEM与MT子集的数据量和数据类型是不一样的,CSEM子集包含电磁场的振幅和相位,MT子集包含TE、TM模式的视电阻率和相位,但是这种方法对将CSEM和MT数据集放入一个数据集中进行反演仍将是有用的,同时,该方法也可用于大地电磁测深数据和地震数据的联合反演^[23,24]. ...

起伏地形大地电磁二维反演

2016

起伏地形大地电磁二维反演

2016

Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator

1996

... 对模型进行有限元正演计算,CSEM正演得到的是E_y的幅值和相位的响应值,MT正演得到的是TE、TM模式的视电阻率和相位的响应值,对得到的响应值添加4%的随机高斯噪声,则生成了反演计算所需的观测数据.反演的初始模型包含空气、海水和海底地层,其中空气和海水电阻率不参与反演,给定地层的初始电阻率为1.0 Ω·m.计算区域所划分的单元越多,所需要的计算量越大,因此只对目标反演区域采用较细的网格剖分,其余部分则采用粗网格以减少不必要的计算量.如图4所示,选取y范围为-4.5~4.5 km海底到5 km深的区域,调用Triangle程序^[25]对该区域进行精细网格剖分,共生成3 756个三角单元,其余部分共剖分为440个三角形单元. ...

... 对初始模型进行剖分,如图11所示,根据接收点和发射点的位置分布对异常体或构造可能存在的区域进行精细网格剖分,其余部分则采用不加约束的粗网格剖分.精细网格的剖分可以保证计算的精度,采用粗网格则可以减少不必要的计算量.调用Triangle程序^[25]对反演区域剖分,最终剖分得到 6 089 个三角单元. ...

〈

〉