0 引言
传统液化判别和危害程度评价方法大多是基于宏观地震灾害现象资料,结合现场试验和室内试验结果,通过总结分析和统计得出的一般规律[5]。如根据剪切波速法、标准贯入法及静力触探法等得出的结果与规范中给出的临界值比较,从而判别是否液化。国内外用于砂土液化的判别方法种类繁多,但由于砂土液化的影响因素多且复杂,因此每种方法都有一定的适用范围和局限性。
砂土液化问题本质上可视为机器学习中的分类问题。近些年来,更多的国内外学者在理论方法和实测数据的基础上,综合多个砂土液化的影响因子,采用不同的分类算法研究砂土液化判别问题。如人工神经网络[6]、支持向量机[7]、距离判别法[8]、Fisher判别模型[9]等方法都被应用到砂土液化预测中。但由于地震作用的随机性、土层参数的多样性,以及没有足够多的样本数据支撑,使得这些算法均存在一定程度上的局限性,如容易陷入局部极小值,或存在过拟合现象。笔者整理了唐山大地震的砂土液化现场资料,选取了其中的72个场地的实际数据,采用机器学习中的随机森林分类算法,并通过数据留出集与交叉验证的测试方式降低模型的过度学习能力,防止出现过拟合现象,一定程度上提高了模型预测的稳定性。
1 随机森林算法的基本原理
随机森林算法是机器学习当中比较常用的分类算法,包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定[10]。因此,有必要简单地介绍下决策树的分类算法和原理。
1.1 决策树分类原理
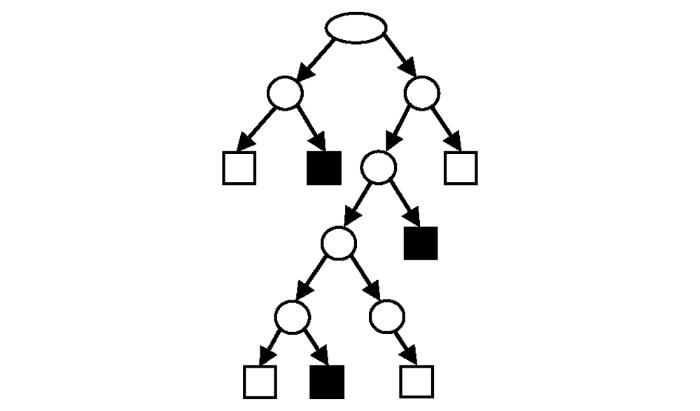
图1
常见的决策树算法主要有基于信息熵的ID3算法、基于信息增益比的C4.5算法和基于Gini系数的CART算法。其中C4.5算法在ID3算法基础之上,用信息增益比替代了信息增益,改善了ID3算法由于信息增益在可取数值数目较多的属性上存在的倾向性问题。
本文采用的是二叉树CART算法,该算法主要以Gini系数作为分裂标准,选择具有最小Gini系数的属性作为节点,节点处的Gini系数值越小,说明该节点数据类别越少,数据集不纯度越低,越有利于划分类别。因此构造CART决策树的过程实质上就是层层递归直到某节点Gini系数最低,即认为该节点可视为叶子节点,从而对样本数据集进行分类。
假设数据集D(X,Y)包含m个类别的样本,样本数量为K,则数据集D的Gini系数值定义为[10]:
式中,p(i|t)表示节点t处当前数据集中类别i的概率。Gini值直观地反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,该值越小,则表示数据集D的纯度越高。而CART算法将数据集D按照某个特征A划分为两个子数据集D1和D2,则此时在特征A条件下,数据集D的Gini系数值定义如下:
CART算法根据某个特征取值下当前数据集的最小Gini系数将数据集划分,生成左右两个子节点,再分别对两个子节点当中的数据集执行相同操作,层层递归,直至叶子节点。不难发现,当决策树的高度无限制地生长时,必然能使得Gini系数为零,此时一定可以将训练数据当中的每个样本都能精确地划分类别。因此,不可避免地带来模型的过拟合问题,使得模型的预测能力下降或不稳定。
1.2 随机森林分类原理
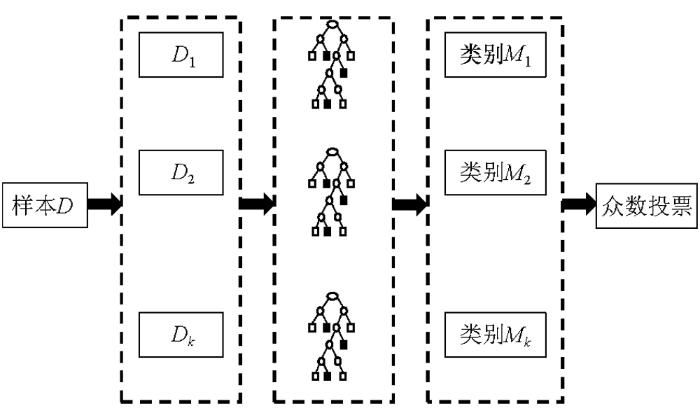
1)从包含M个特征的总样本数据集D中采用有放回采样随机选取k个子训练集(D1,D2,…,Dk),用于构造k个决策树。
2)对每个决策树的每个节点,随机选取n个特征(n应小于M)计算当前的Gini系数作为分裂子节点的优选特征,让决策树完整生长,直至Gini系数最小到达叶子节点。
3)遍历所有决策树,得到每个决策树的分类结果,采取众数投票结果作为最终的分类模型,对未知数据进行预测。
图2
2 随机森林砂土液化预测模型
2.1 砂土液化判别指标
2.2 数据预处理
2.2.1 数据标准化
由于各指标之间的量级差异比较明显,因此需要进行标准化处理以消除量纲的影响。本次采用式(3)所示的z-score法进行标准化:
式中:μ和σ分别为样本均值和标准差。标准化之后的数据无量纲,均值为0,标准差为1。
2.2.2 数据集划分
表1 砂土液化训练样本集
Table 1
| 序号 | 判别指标 | 液化情况 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| I | L/km | D50/mm | Cu | dw/m | ds/m | N63.5/击 | τd/ | ||
| 1 | 7 | 68.6 | 0.410 | 2.90 | 1.09 | 4.15 | 5 | 0.1000 | 1 |
| 2 | 7 | 83.3 | 0.187 | 4.00 | 1.20 | 2.45 | 8 | 0.0900 | 1 |
| 3 | 7 | 83.3 | 0.111 | 2.02 | 0.80 | 1.35 | 6 | 0.0800 | 1 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 19 | 7 | 79.0 | 0.120 | 1.55 | 1.37 | 3.60 | 19 | 0.0940 | 0 |
| 20 | 7 | 81.2 | 0.160 | 2.67 | 1.05 | 4.30 | 12 | 0.1050 | 0 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 26 | 8 | 116.4 | 0.200 | 2.70 | 1.60 | 8.70 | 8 | 0.2120 | 1 |
| 27 | 8 | 116.4 | 0.170 | 1.91 | 3.30 | 5.80 | 5 | 0.1600 | 1 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 43 | 8 | 70.9 | 0.300 | 2.43 | 2.30 | 12.30 | 13 | 0.2030 | 0 |
| 44 | 8 | 47.0 | 0.310 | 2.42 | 2.00 | 3.46 | 8 | 0.1630 | 0 |
| 45 | 8 | 117.0 | 0.073 | 7.50 | 1.53 | 11.90 | 26 | 0.2170 | 0 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 50 | 9 | 22.0 | 0.200 | 1.94 | 0.43 | 2.61 | 10 | 0.4620 | 1 |
| 51 | 9 | 22.0 | 0.240 | 2.08 | 1.15 | 4.50 | 22.2 | 0.4150 | 1 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 62 | 9 | 14.0 | 0.160 | 2.25 | 4.90 | 9.38 | 61 | 0.3180 | 0 |
| 63 | 9 | 9.6 | 0.210 | 3.15 | 3.50 | 8.35 | 31 | 0.3470 | 0 |
| 64 | 9 | 11.0 | 0.160 | 2.76 | 4.50 | 4.50 | 22 | 0.2480 | 0 |
表2 砂土液化测试样本集
Table 2
| 序号 | 判别指标 | 液化情况 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| I | L/km | D50/mm | Cu | dw/m | ds/m | N63.5/击 | τd/ | ||
| 1 | 7 | 76.8 | 0.166 | 1.65 | 0.50 | 1.70 | 3 | 0.1000 | 1 |
| 2 | 7 | 60.8 | 0.360 | 3.30 | 1.59 | 6.65 | 23 | 0.1030 | 0 |
| 3 | 7 | 70.0 | 0.145 | 8.50 | 0.85 | 1.80 | 2 | 0.0890 | 1 |
| 4 | 7 | 49.0 | 0.140 | 2.31 | 1.00 | 4.80 | 14 | 0.1080 | 0 |
| 5 | 7 | 81.2 | 0.140 | 1.60 | 1.40 | 4.35 | 9 | 0.1000 | 1 |
| 6 | 8 | 116.0 | 0.265 | 2.81 | 3.30 | 13.80 | 17 | 0.1900 | 0 |
| 7 | 8 | 117.4 | 0.134 | 2.23 | 3.20 | 7.20 | 8 | 0.1720 | 1 |
| 8 | 9 | 17.0 | 0.185 | 1.90 | 0.61 | 3.80 | 4 | 0.4580 | 1 |
2.2.3 学习过程
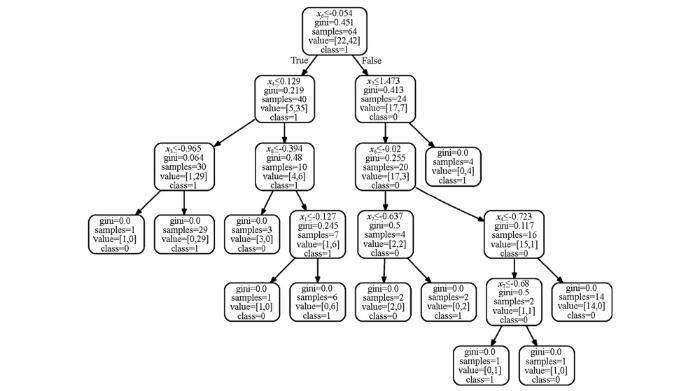
对于随机森林算法中的单棵决策树来说,对当前数据集选择某一种属性特征计算Gini系数作为分裂子节点的优选特征。图3所示为砂土液化预测单棵6层决策树模型。首先,选定归一化后的标准贯入击数N63.5(x6)作为根节点,以x6≤-0.054为判定条件计算Gini系数为 0.451,此时64个样本被划分为两类,分别为22个和42个。以此为根节点,生长决策树,产生第二层子节点,其中左节点以x4≤0.129为判定条件,选择地下水位dw为优选特征,样本分别为5个和35个,而右节点选择以x7≤1.473为判定条件,选择剪应力与有效上覆应力比为优选特征,样本分别为17个和7个;两个子节点的Gini系数分别为0.219和0.413。相对于根节点的数据集而言,不纯度降低,说明决策树的生长方向是有利于类型划分的。以此类推,直到数据集的Gini系数为零,决策树终止生长。不难发现,随着决策树的高度增加,当前数据集的样本量也在减少,因此需要注意的是:当不对决策树的高度和当前节点的最小样本量加以控制时,决策树的规模和计算量会相应地增加,虽然最终能够对每一个样本进行准确地类型划分,但不可避免地增加了过拟合的风险。因此有必要抑制决策树的生长,对模型进行适当的优化。而随机森林算法在决策树的基础上增加了多个分类器模型,避免了单棵决策树由于分类过度带来的过拟合风险。
图3
2.3 模型优化
2.3.1 剪枝处理
虽然随机森林相比于单个决策树分类器来说,通过众数投票的方式在一定程度上能够避免过拟合问题,但如果随机森林当中的每个决策树不加以控制和修剪,必然会带来总体的预测误差及不稳定性。因此,适当地对决策树的生长加以控制,能够提高最终模型的预测稳定性。本次采取预剪枝方法控制决策树的高度和最大叶子节点数[11]来控制决策树的生长,防止出现过拟合现象。
2.3.2 交叉验证
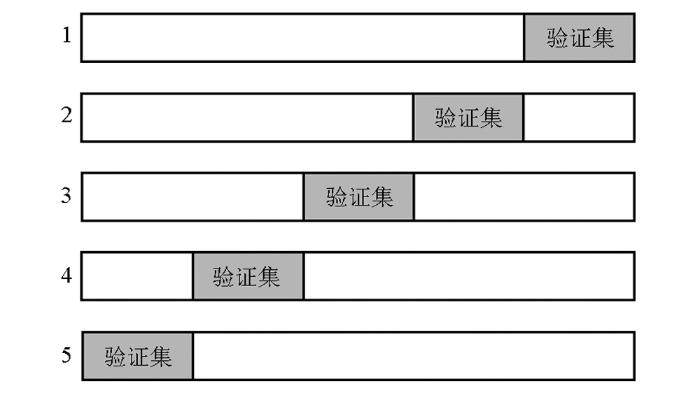
在样本量不足够多的情况下,如果将训练集全部参与学习训练,必然导致学习能力过剩和模型的过拟合。因此,有必要使用留出集的方式从训练集当中随机选取部分数据作为验证集,通过多次交叉验证的方式,让数据的每个子集既是训练集,又是验证集,从而更好地评估模型性能和稳定性。图4为五轮交叉验证的示意。
图4
2.4 预测结果
图5
图5
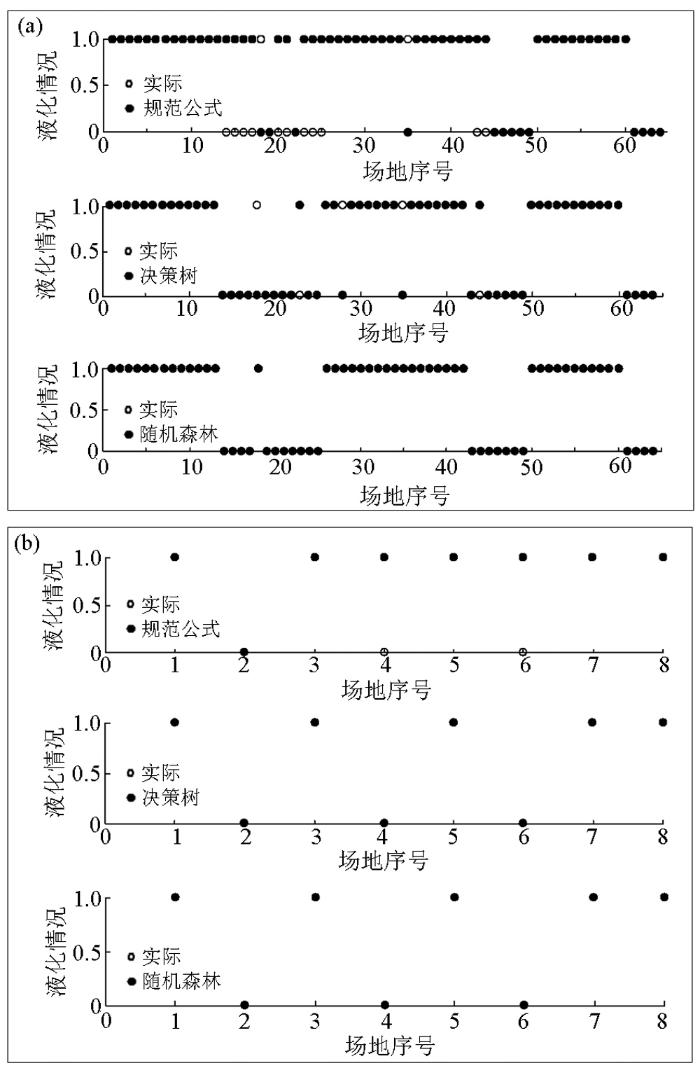
模型训练(a)及预测结果(b)
Fig.5
Training results(a) and test results(b) of prediction model
图5中空心圆表示实测液化结果,实心圆表示不同方法的预测结果。不难发现,抗震规范中的基于标贯试验的计算公式误判率较高,在训练样本上有13个样本误判,误判率为20.3%,在预测样本上有2个样本误判,误判率为25%。而决策树和随机森林模型的训练结果和预测结果明显高于规范公式的计算结果,在预测样本上均没有出现误判。但单个决策树模型在训练样本上有5个样本误判,误判率为7.8%,稳定性明显不如随机森林预测模型。
3 结论
本文选取了8个影响砂土液化的判别指标,以唐山大地震中72个场点液化情况的实测样本为例,探讨了机器学习中的决策树和随机森林模型在砂土液化预测中的可行性。研究结果表明,与抗震规范中的标贯试验判别公式相比,决策树和随机森林预测模型的成功率有了明显的提高,尤其是随机森林预测模型,在多个决策树分类的基础上降低了样本学习的过拟合风险,提高了模型的预测稳定性,可以在今后砂土液化判别工作中予以推广。
参考文献
基于PCA-DDA原理的砂土液化预测模型及应用
[J].
Discrimination model of sandy soil liquefaction based on PCA-DDA principle and its application
[J].
砂土地震液化的模糊概率评判方法
[J].
Fuzzy probability comprehensive evaluation method for sand liquefaction during earthquake
[J].
关于修改抗震规范砂土液化判别式的几点意见
[J].
Some opinions on the modification of sand liquefaction discriminant of seismic code
[J].
以标贯试验为依据的砂土液化确定性及概率判别法
[J].
Deterministic and probabilistic triggering correlations for assessment of seismic soil liquefaction at nuclear power plant
[J].
砂土地震液化预测的人工神经网络模型
[J].
Artificial neural network model for prediction of seismic liquefaction of sand soil
[J].
基于聚类—二叉树支持向量机的砂土液化预测模型
[J].
Support vector machine model for predicting sand liquefaction based on clustering binary tree algorithm
[J].
基于逐步判别分析的砂土液化预测研究
[J].
Sand liquefaction prediction based on stepwise discriminant analysis
[J].
砂土液化预测的Fisher判别模型及应用
[J].
Fisher discriminant analysis model of sand liquefaction and its application
[J].
基于改进网格搜索算法的随机森林参数优化
[J].
Parameter optimization method for random forest based on improved grid search algorithm
[J].