0 引言
时频分析是研究非平稳信号的重要手段[1],它们在地震勘探中有着广泛的应用[2,3], 如地震波能量吸收衰减补偿、储层预测、地震旋回分析、属性提取等在各个领域都得到了广泛的应用。S变换是介于短时傅里叶变换和小波变换之间的一种时频分析方法,具备小波变换的多分辨率特性,克服了短时傅里叶变换不能调节分析窗口的缺点,不需要满足小波容许条件,变换结果与傅里叶谱保持直接的联系[4]。广义S变换改造了标准的S变换,使它能根据实际应用中非平稳信号的频率分布特点和时频分析的侧重点,灵活地调节小波随频率尺度的变化趋势,不但可以进一步加快或减慢小波的时宽随信号频率变换的速度,而且使小波的振幅呈现多种变化特征,使广义S变换能够更好地适应具体信号的分析和处理[5]。
由于地震资料不受井点位置的限制, 本文通过对地震信号进行时频分析,并把时频谱变换到时频域Teager-Kaiser能量谱,进而求取时频域Teager-Kaiser能量峰值频率属性曲线,对其结果用于沉积旋回划分。关于这方面的工作,前人涉及的不多。本文通过对四种沉积模型的时频属性的计算,验证了基于广义S变换时频属性曲线划分沉积旋回的可靠性;然后对实际地震资料进行处理,以井旁地震道作为研究对象,根据其尺度的大小,选择合适的滤波器对计算的基于Teager-Kaiser能量算子的峰值频率属性曲线进行分频滤波,再进行长期旋回和短期旋回的划分,测井资料的验证效果良好。实际应用证明, 本文的方法具有较高的精度和可靠性,且不受井点位置的制约,有利于研究地层横向变化的特征。
1 技术方法
1.1 广义S变换
两个参数λ和p是式(1)中广义S变换窗函数的两个调节因子。相比于Gabor变换、S 变换,广义S变换的两个调节因子可灵活调节小波随频率尺度f的多种非线性变化特征[14],使得广义S变换更好地适应具体复杂时变信号的处理和分析。
1.2 Teager-Kaiser能量算子
对于单频地震能量密度, Teager-Kaiser能量算子的表达式[6]为:
式中:E为地震能量,A为振幅,ω为角频率,ρ为密度,f为频率。利用模拟质点—弹簧物理模型,Kaiser推导出了离散形式的信号能量表达式[7]:
式中:m是物体的质量,x[n]是离散时间信号的采样序列。式(2)和式(3)的差别之处在于地震能量密度中的ρ和弹簧模型中的质量m,两者在本质上是相同的,因此利用式(3)计算地震信号的Teager-Kaiser能量,而式(3)对于单频信号是严格成立的。将广义S变换与Teager-Kaiser能量算子进行结合,计算地震波的瞬时能量谱,展布地震能量的时频分布特征。离散地震信号各单频的Teager-Kaiser能量计算公式如下:
式中:j为时间样点号,k为频率样点号。对于一道地震数据,进行广义S变换时频分析就可得到时频谱。对时频谱的每一道数据(每一单频分量)应用上述Teager-Kaiser能量算子,便得到Teager-Kaiser能量分布。
2 沉积模型试算
沉积旋回是指沉积作用和沉积条件按相同的次序不断重复沉积而组成的一个层序[15]。通常细颗粒沉积速率小,形成的沉积层较薄,粗颗粒沉积速率大,形成的沉积层较厚;层理结构中尺度变化及变化的方向性决定了其地震响应频率成分的不同。时频分析是地震层序分析的重要手段,阐明了各级地震层序体内部的精细结构, 并预测其物质成分[16]。时频分析提供了时间域和频率域联合分布的信息,地质上的旋回性对应着地震数据上时频域的变化特征。为了探索时频分析技术在沉积旋回方面的分析效果,设计了如下4种典型的沉积旋回模型,其速度参数由实际测井资料的统计得到[17],砂岩速度范围为3 000~3 400 m/s,泥岩的速度约为2 500~2 900 m/s。单层砂岩速度分别为3 000、3 050、3 100、3 150、3 200、3 250、3 300、3 350、3 400 m/s,与之对应的时间厚度依次为16、24、32、40、48、56、64、72、80 ms;单层泥岩的速度分别为2 500、2 550、2 600、2 650、2 700、2 750、2 800、2 850、2 900 m/s, 与之对应的时间厚度依次为12、18、24、30、36、42、48、54、60 ms,子波为主频25 Hz的雷克子波, 在地质上为砂岩、泥岩呈互层发育。
2.1 正旋回
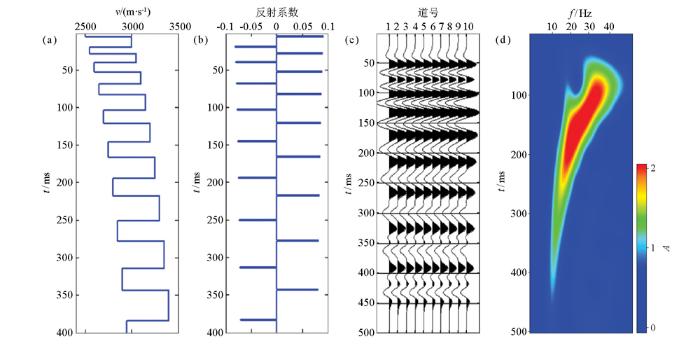
正旋回模型,砂岩、泥岩呈现互层发育,单层厚度随深度从深到浅逐渐变薄。该模型反映了自下而上水动力条件从强到弱、沉积物颗粒由粗变细的退积型沉积环境。 图1为正旋回模型及其地震响应。时频分析结果清晰地指示出正旋回的时频特征,频率随厚度减小而增大,即旋回顶部富含高频成分、底部富含低频成分。
图1
图1
正旋回模型及其地震响应
a—速度模型;b—反射系数;c—合成地震记录;d—时频谱
Fig.1
Normal cycle model and its seismic response
a—velocity model;b—reflection coefficient;c—synthetic;d—time-frequency spectrum
2.2 反旋回
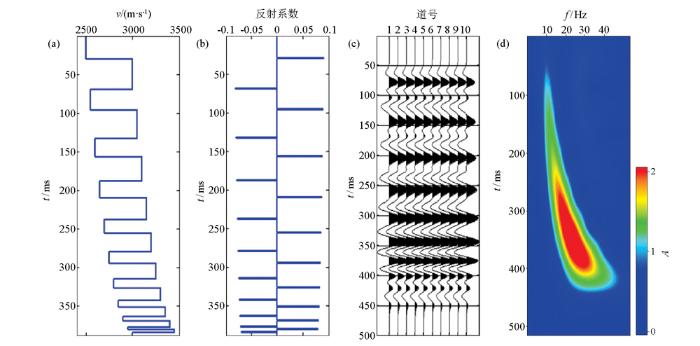
反旋回模型,砂岩、泥岩呈互层发育,单层厚度随深度从深到浅逐渐变厚,反映了水动力条件自下而上从弱到强、沉积物颗粒由细到粗的进积型沉积环境。图2为反旋回模型及其地震响应。时频分析结果清晰地指示出反旋回的时频特征,频率随厚度增大而减小,即旋回顶部富含低频成分、底部富含高频成分。
图2
图2
反旋回模型及其地震响应
a—速度模型;b—反射系数;c—合成地震记录;d—时频谱
Fig.2
Inverse cycle model and its seismic response
a—velocity model;b—reflection coefficient;c—synthetic;d—time-frequency spectrum
2.3 反正旋回
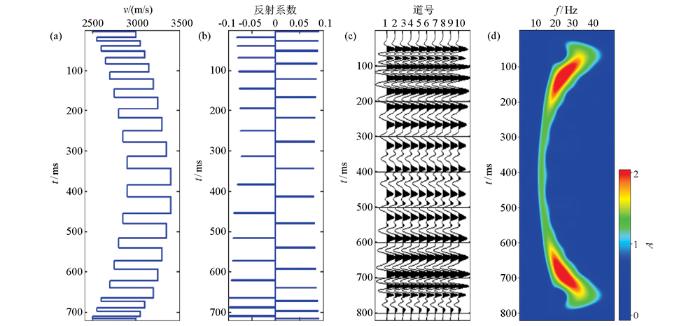
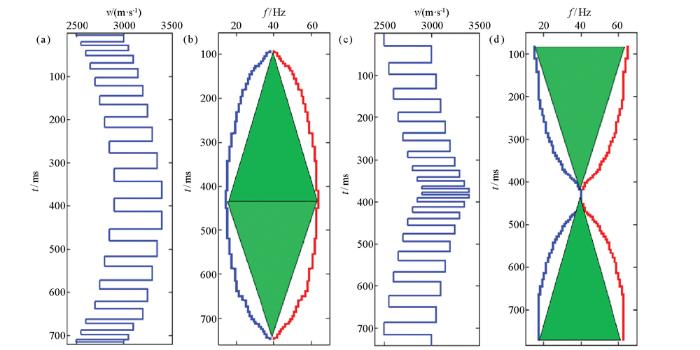
反正旋回模型,砂岩、泥岩互层组的厚度,由深至浅先增大再减小。先进行反旋回沉积再进行正旋回沉积,反映了一种进积—退积复合沉积环境。图3为反—正旋回模型及其地震响应。时频分析结果表明由深到浅, 频率变化趋势为高→低→高,即旋回顶部和底部富含高频成分,中间富含低频成分。
图3
图3
反正旋回模型及其地震响应
a—速度模型;b—反射系数;c—合成地震记录;d—时频谱
Fig.3
Inverse-normal cycle model and its seismic response
a—velocity model;b—reflection coefficient;c—synthetic;d—time-frequency spectrum
2.4 正反旋回
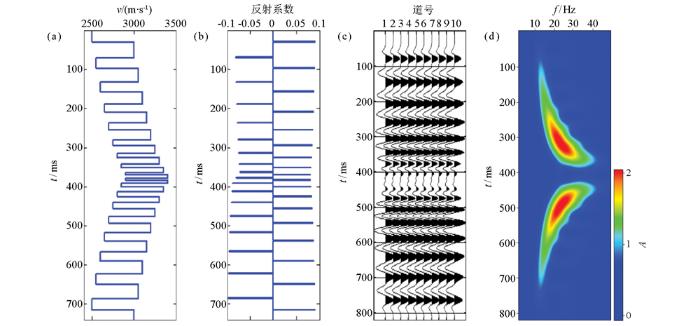
正反旋回模型中,砂岩、泥岩互层组的厚度,从深到浅先减小再增大。先进行正旋回沉积再进行反旋回沉积,反映了一种退积—进积复合沉积环境。图4为正—反旋回模型及其地震响应。时频分析结果清晰地指示出由深到浅,频率变化趋势为低→高→低,表明旋回的顶部和底部富含低频成分,中间富含高频成分。
图4
图4
正反旋回模型及其地震响应
a—速度模型;b—反射系数;c—合成地震记录;d—时频谱
Fig.4
Normal-inverse cycle model and its seismic response
a—velocity model;b—reflection coefficient;c—synthetic;d—time-frequency spectrum
2.5 旋回模型试算
图5
图5
反正旋回模型及其峰值频率镜像图、正反旋回模型及其峰值频率镜像图
a—反正旋回模型;b—模型a的峰值频率镜像图;c—正反旋回模型;d—模型c的峰值频率镜像图
Fig.5
Inverse-normal cycle model and its peak frequency mirror image、normal-inverse cycle model and its peak frequency mirror image
a—inverse-normal cycle model;b—peak frequency mirror image of model a;c—normal-inverse cycle model;d—peak frequency mirror image of model c
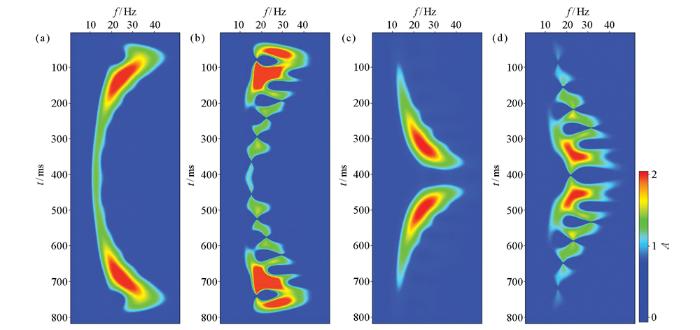
峰值频率属性曲线在时间方向上一定程度反映了地质结构的变化,但是对地层微观结构的变化和时间的定位不够精准。如图5所示的反正旋回模型砂岩、泥岩互层组的厚度,由深至浅先增大再减小,由深到浅, 频率变化趋势为高→低→高。但是在每一个砂泥岩组内,砂岩和泥岩厚度变化的不同在峰值频率曲线上无法精准定位。正反旋回模型亦有相同的结论。为了得到时频谱上反映地层微观结构变化的信息,本文在广义S变换时频分析的结果上引入Teager-Kaiser能量算子。具体实现过程是:利用式(4)对图6a、6c所示的广义变换时频谱进行计算,求取时频域Teager-Kaiser能量谱如图6b、6d所示。在时间方向上Teager-Kaiser能量谱和广义S变换谱的低频变化趋势一致,但是Teager-Kaiser能量谱在细节上表征了在砂泥岩组内,砂岩和泥岩厚度变化的不同,更具刻画薄层结构的变化。
图6
图6
旋回模型TK能量谱试算
a—反正旋回时频谱;b—反正旋回TK能量谱;c—正反旋回时频谱;d—正反旋回TK能量谱
Fig.6
TK energy spectrum test of cycle model
3 应用实例
图7
图7
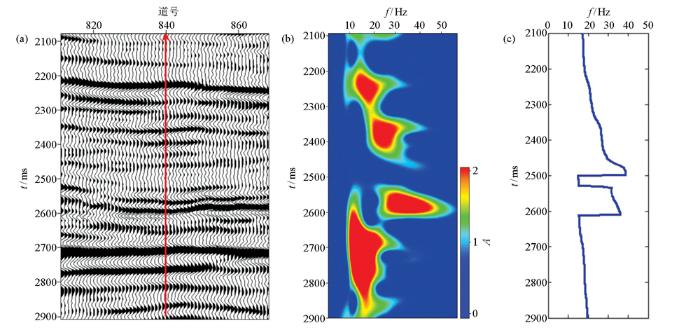
地震剖面、井旁道时频谱及峰值频率属性曲线
a—地震剖面;b—井旁道时频谱;c—井旁道峰值频率曲线
Fig.7
Seismic profile、seismic trace time-frequency spectrum cross well and peak frequency curve
a—seismic profile;b—seismic trace time-frequency spectrum cross well;c—peak frequency curve cross well
图8
图8
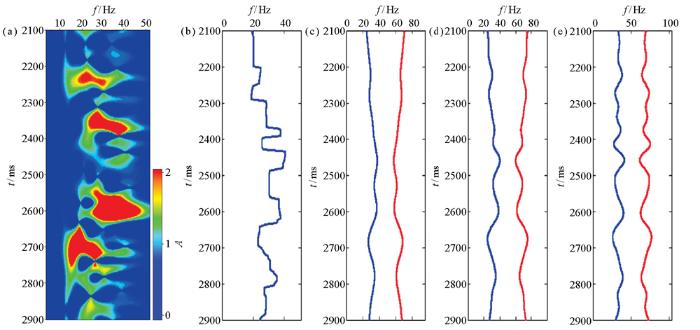
T-K能量谱、T-K峰值频率曲线及其分频曲线
a—T-K能量谱;b—T-K峰值频率曲线;c—曲线b低频分量;d—曲线b中频分量;e—曲线b高频分量
Fig.8
T-K energy spectrum、T-K peak frequency curve and its frequency-division curve
a—T-K energy spectrum;b—T-K peak frequency curve;c—low frequency component of b;d—intermediate frequency component of b;e—high frequency component of b
3.1 中、长期旋回划分效果
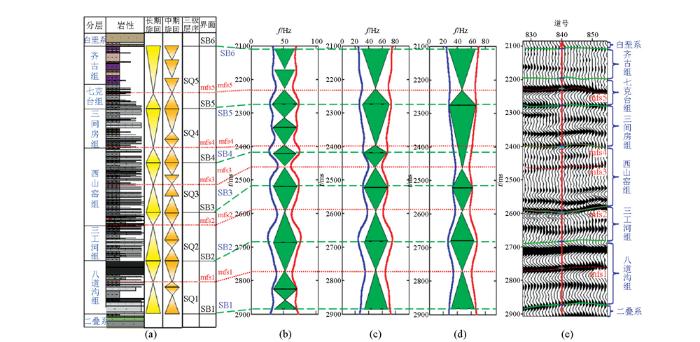
利用图8b所示的时频域Teager-Kaiser峰值频率曲线进行沉积旋回划分。首先对该曲线进行分频滤波。根据需要研究的沉积旋回级别(周期T),进而确定所要求取的沉积旋回曲线的中心频率(F=1/T)。由此设计带通滤波器。图8c中蓝色曲线为对该曲线进行低通滤波后的属性曲线、图8d中蓝色曲线为对该曲线进行带通滤波后的中频分量属性曲线,红色曲线为该曲线的镜像曲线。图9c、9d分别为根据滤波后的属性曲线图8c、8d进行中期、长期旋回划分结果。根据前人研究成果以及时深标定对过井地震剖面图进行了解释如图9e所示,其中图9e中的绿色实线为对应于图9a的分层界面,红色虚线为对应于图9a基于岩性进行解释的最大湖泛面。基于本文方法的长期旋回划分结果(图9d),可以识别图9a中4个最大湖泛面,分别为mfs1、mfs2、mfs3、mfs5,而且在界面SB1至SB3部分, 界面SB5至SB6部分和基于岩性解释的长期旋回划分结果(图9a长期旋回划分结果)具有较高的一致性。基于本文方法的中期旋回划分结果(图9c),可以识别图9a中5个(全部)最大湖泛面,而且在界面SB1至SB6和基于岩性解释的长期旋回划分结果(图9a长期旋回划分结果)吻合。验证了文中的方法用于中期、长期旋回划分的可靠性。
图9
图9
基于前人结果及时深标定对过井地震剖面解释结果
a—地质分层、岩性及基于岩性划分的旋回;b—短期旋回;c—中期旋回;d—长期旋回;e—过井地震剖面
Fig.9
Cross-well section interpretation results based on time depth calibration and previous results
a—geological stratification,lithology and cycle based on lithology division;b—short-term cycle;c—medium-term cycle;d—long-term cycle;e—seismic profile
3.2 短期旋回划分效果
选择井旁道时频域Teager-Kaiser峰值频率属性曲线的高频分量(图8e)进行沉积旋回划分。如图9b所示,基于文中方法短期旋回划分的结果和基于岩性短期旋回划分的结果进行对比。本文方法短期旋回划分结果(图9b)可以识别图9a中5个(全部)最大湖泛面。在界面SB1至SB2部分,本文方法短期旋回划分结果和基于岩性的短期旋回划分的结果精度相当,但是在界面SB2至界面SB4部分,本文的短期旋回划分结果精度略低于基于岩性短期旋回划分结果。在界面SB4至界面SB5部分,本文的短期旋回划分结果和基于岩性短期旋回划分结果相当。在界面SB5至界面SB6部分,本文的短期旋回划分结果略低于基于岩性短期旋回划分结果,略高于基于岩性短长期旋回划分结果。
4 结论
1)针对文中设计的理论模型,应用基于广义S 变换时频谱峰值频率属性曲线进行沉积旋回划分与设计的理论模型相吻合。
2)实际资料应用中,在时频谱上应用Teager-Kaiser能量算子,可以得到进一步反映地层微观结构变化的信息,求取的Teager-Kaiser峰值频率属性曲线为后续的沉积旋回划分提供精度较高的基础数据。
3)通过对Teager-Kaiser峰值频率属性曲线进行分频滤波,基于滤波后的数据进行沉积旋回划分的方法,可以得到基于地震资料的分级沉积旋回划分结果,减少了人为的主观因素,提高了旋回划分的可靠性。
4)在低勘探程度地区因测井资料比较少或分布不均匀导致难以确定层序界面的情况下,可以求取基于Teager-Kaiser能量属性的峰值频率属性方法进行沉积旋回划分,进而为地层沉积期次划分和地层精细对比提供参考。
参考文献
时频分析技术在石油地球物理勘探中的应用
[J].
Application of time-frequency analysis in geology
[J].
希尔伯特—黄变换地震信号时频分析与属性提取
[J].
Seismic signal time-frequency analysis and attributes extract based on HHT
[J].
Localization of the complex spectrum:the S transform
[J].
基于广义S变换的地震资料高效时频谱分解
[J].
High efficient time-frequency spectrum decomposition of seismic data based on generalized S transform
[J].
Evidence for nonlinear production mechanisms in the vocal tract
[J].
On a simple algorithm to calculate the 'energy' of a signal
[J].
Teager energy based feature parameters for speech recognition in car noise
[J].
Power spectrum difference teager energy features for speech recognition in noisy environment
[C]//
Wavelet transform Teager-Kaiser energy applied to a carbonate field in Brazil
[J].
沉积旋回的地球物理研究
[J].
Geophysical study of sedimentary cycles
[J].
砂砾岩体沉积旋回划分方法及对比方法——以济阳坳陷盐家地区沙四段上亚段为例
[J].
Sedimentary cycle division and correlation of sand-conglomerate body in upper Sha IV Formation of Yanjia area, Jiyang depression
[J].
利用小波深频分析方法研究地层沉积旋回
[J].
Study of sedimentary reservoir cycles using wavelet depth-frequency analysis method
[J].
广义S变换地震高分辨率处理方法研究
[J].
High-resolution seismic processing based on generalized S transform
[J].
应用Hilbert-Huang变换方法研究等时小层划分及对比
[J].
Application of Hilbert-Huang transform to study classification and correlation of isochrones substratum
[J].
The division of sedimentary cycle based on HHT
[C]//