基追踪弹性阻抗反演识别含气砂岩

doi:10.11720/wtyht.2020.1427

基追踪弹性阻抗反演识别含气砂岩

郝亚炬^,¹, 高君²

1.东华理工大学地球物理与测控技术学院,江西南昌 330013

2.中国石油化工有限公司勘探开发研究院,北京 100083

Gas sand prediction using basis pursuit elastic impedance inversion

HAO Ya-Ju^,¹, GAO Jun²

1. School of Geophysics and Measurement-Control Technology,East China University of Technology,Nanchang 330013,China

2. Petroleum Exploration and Production Research Institute,SINOPEC,Beijing 100083,China

责任编辑: 叶佩

收稿日期: 2019-11-10 修回日期: 2020-09-10 网络出版日期: 2020-12-20

基金资助:

国家重大专项子课题. 2016ZX05033-02
中国石油天然气集团公司科学研究与技术开发项目“大型地震处理解释软件平台开发与集成”. 2016E-1004

Received: 2019-11-10 Revised: 2020-09-10 Online: 2020-12-20

作者简介 About authors

郝亚炬(1990-),男,讲师,博士,主要从事地震反演理论与算法等方面的研究工作。Email:haoyj_13@163.com

摘要

砂岩储层含气后地震波阻抗会显著降低,因此阻抗反演是对含气砂岩储层进行预测的常用方法。但砂岩储层的波阻抗值不仅取决于含流体性质,还与岩石的孔隙度、矿物结构组分等多种因素有关,即使砂岩储层含气,其波阻抗也可能高于高孔含水砂岩,因此,叠后地震阻抗反演结果在含气砂岩储层预测中存在较强的多解性。由于利用了含气砂岩的AVO异常特性,叠前弹性阻抗在含气砂岩储层预测中比叠后地震阻抗具有更高的可靠性。为了提高弹性反演结果的精度,将基追踪反演(basis pursuit inversion,BPI)算法引入叠前弹性阻抗反演。该方法是将地震信号投影到奇、偶子波库上,通过投影值求得每道的相对反射系数,然后进行道积分得到相对弹性波阻抗。相比于传统的稀疏脉冲反演(sparse spike inversion,SSI)算法,基追踪弹性反演算法不需要建立初始低频模型,可显著提高薄层分辨能力和反演精度。通过合成信号的试算和实际地震数据的反演表明,基追踪叠前弹性反演可有效地对砂岩储层的含气异常进行检测,并且相比于传统SSI算法具有更高的反演精度。

关键词： 基追踪反演 ; 弹性阻抗 ; 角道集 ; 含气砂岩预测

Abstract

The impedance of sand reservoir will become lower if the pores are filled with natural gas,so the gas reservoir can be detected by using impedance inversion,which is a common used method.However,the impedance of sand reservoir can be influenced by many kinds of factors such as porosity and mineral composition.As a consequence,the impedance of gas sand may be higher than that of high porosity brine sandstone.In this case,mistake would be caused if post-stack impedance is only used to predict gas sand.Elastic impedance is more reliable than acoustic impedance,because gas sand reservoir can induce AVO anomaly.Simultaneously,in order to improve inversion resolution and accuracy,the authors introduce BP (Basis Pursuit) algorithm to complete elastic inversion.This algorithm is used to decompose seismic signal to even and odd wavelet dictionaries and then reflection coefficient can be obtained by the decomposition coefficients.The method proposed by the authors doesn't need initial low frequency model that traditional inversion method SSI (Sparse Spike Inversion) has to know beforehand. In this case,resolution and accuracy can be improved.The application to synthetic data and field data indicates that this method is more accurate than SSI.

Keywords： basis pursuit inversion ; elastic impedance ; angle seismic gather ; gas sand prediction

PDF (6904KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

郝亚炬, 高君. 基追踪弹性阻抗反演识别含气砂岩. 物探与化探[J], 2020, 44(6): 1329-1335 doi:10.11720/wtyht.2020.1427

HAO Ya-Ju, GAO Jun. Gas sand prediction using basis pursuit elastic impedance inversion. Geophysical and Geochemical Exploration[J], 2020, 44(6): 1329-1335 doi:10.11720/wtyht.2020.1427

0 引言

叠前地震资料比叠后地震资料包含了更多的储层物性信息,这是由于纵、横波速度和密度同时决定了储层的叠前地震响应特征(振幅随角度的变化),而叠后地震资料被视为自激自收的地震记录,只由纵波速度和密度决定,缺乏横波信息。因此叠前弹性反演(elastic inversion)结果相比于叠后阻抗反演(impedance inversion)能够更有效地突出砂岩储层的含气异常,有利于与高孔含水砂岩进行区分。

弹性反演在含气砂岩储层预测中具有较为广泛的应用。Connolly从理论上定义了弹性阻抗,并解释了大角度弹性阻抗可更好地突出含油气储层低阻异常的原因,通过分析计算表明:随着入射角度的增大,含气砂岩储层弹性阻抗逐渐降低^[1]。He Fu-bang等将岩石物理分析与弹性反演相结合,对含气砂岩储层进行了预测^[2]。

目前,各种商业软件中弹性反演的核心算法大多是稀疏脉冲算法(SSI),该方法需要利用测井数据和层位数据建立初始低频阻抗模型,然后通过多次迭代对初始模型进行优化,在最小二乘意义下的最优解即为最终阻抗反演结果^[3]。初始模型的形态依赖于层位的形态,而层位追踪过程中往往追踪地震波形的波峰或波谷。如果地震反射波发生严重的调谐,追踪地震波峰谷所得层位的位置和形态与地下真实的地质界面会产生较大的差异^[4]。对于叠前地震数据,不同阻抗界面的AVO效应差异较大,产生的反射子波振幅变化也较大,因此小角度道集和大角度道集的地震波调谐情况有较大差异,导致波峰和波谷出现的位置不同,不同角度道集建立的初始模型不同,使上述依赖于初始模型的反演变得复杂繁琐。此外,初始模型中的阻抗值是通过测井数据的外推和插值进行计算,如果井震标定不准确,会对初始模型阻抗值产生较大影响。栾颖等指出,不同初始模型所得的反演结果往往不同,初始模型对反演结果影响重大^[5]。换言之,初始模型设置不合理,会使反演结果产生假层或层的缺失,引起错误的解释。

基追踪算法作为一种信号的稀疏分解方法目前已经被广泛应用于信号处理,例如压缩感知、信号重构、噪声压制、模式识别等^[6,7,8],Zhang等将该算法用于叠后、叠前地震反演,提高了地震反演的分辨率和稳定性^[9,10]。为了使弹性阻抗的反演结果不受初始模型的影响,本文将基追踪反演算法用于叠前弹性反演,通过合成数据实验,表明基追踪反演结果在近角和远角地震道上都可以得到十分稳定的反演结果,传统稀疏脉冲算法近角和远角地震道反演结果差异较大,特别是远角道集容易出现“假层”;最后利用基追踪叠前弹性反演结果对实际地震资料进行反演,清楚揭示了含气砂岩储层的分布。

1 方法原理

1.1 地震数据的奇偶子波分解

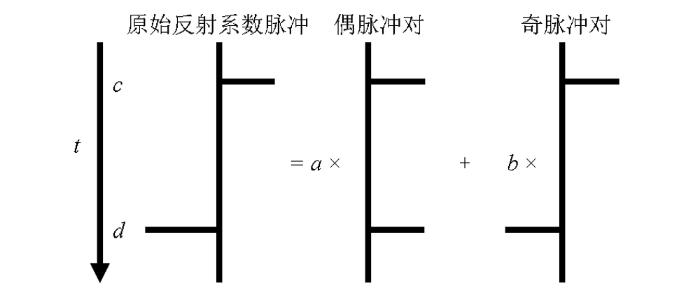
如图1所示,假设某地层的顶、底反射系数可表示为r_l=cδ(t)+dδ(t-nΔt),偶脉冲对r_e与奇脉冲对r_o分别表示为如下的两个函数:

(1)

\{\begin{array}{l} r_{e} = δ (t) + δ (t - n Δ t), \\ r_{o} = δ (t) - δ (t - n Δ t) 。 \end{array}

式中,Δt为时间采样间隔,n为单脉冲之间的间隔点数。根据亥霍姆兹定理,对称区间函数可以分解为一个偶函数和一个奇函数的线性组合(分解过程如图1所示)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 任意反射系数脉冲对的奇偶分解

Fig.1 Any arbitrary pair of reflection coefficients can be represented as the sum of even and odd components

r_l可以表达为如下关系:

(2)

r_{l} = a r_{e} + b r_{o},

将r_l的表达式、式(1)代入式(2)得:

(3)

[\begin{array}{l} c \\ d \end{array}] = [\begin{array}{l} 1 & 1 \\ 1 & - 1 \end{array}] [\begin{array}{l} a \\ b \end{array}],

因此,求得参数a和b即可得到反射系数c和d。

对于奇、偶脉冲对,两个脉冲之间的间隔为nΔt。如果n=1,…,N(N为脉冲之间的最大间隔),则形成奇、偶楔形反射对。每个奇偶脉冲对沿时间轴进行逐点平移,假设平移量为mΔt,m=1,2…,M,M为时间采样点数,则可将式(1)改写为:

(4)

\{\begin{array}{l} r_{e} (t, m, n, Δ t) = δ (t - m Δ t) + δ (t - m Δ t - n Δ t), \\ r_{o} (t, m, n, Δ t) = δ (t - m Δ t) - δ (t - m Δ t - n Δ t) 。 \end{array}

类似于式(2),任意反射系数序列可表示为:

(5)

\begin{array}{l} r (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{m = 1}} {a_{m, n} r_{e} (t, m, n, Δ t) + \\ b_{m, n} r_{o} (t, m, n, Δ t)}, \end{array}

式(5)就是反射系数的奇偶脉冲分解公式,求得系数a_m_,_n和b_m_,_n后即可得到反射系数序列r(t)。

在式(5)两端同时与地震子波w(t)进行褶积可得地震数据的奇偶子波分解:

(6)

\begin{array}{l} s (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{m = 1}} {a_{m, n} w (t) \times r_{e} (t, m, n, Δ t) + \\ b_{m, n} w (t) \times r_{o} (t, m, n, Δ t), \end{array}

式中s(t)为一道地震信号。实际反演过程中,地震信号s(t)和地震子波w(t)都是已知,通过求解式(6)中的系数a_m_,_n和b_m_,_n,代入式(5)即可得反射系数序列。本文所述的基追踪反演算法正是利用这种对地震信号的奇偶子波分解实现无模型反演(或无井反演)。

1.2 基追踪弹性阻抗反演

不同入射角的地震信号之间有较大差异,这种差异主要体现在角道集的振幅特性上,可以由Zoeppritz方程^[11]或Aki-Richards方程^[12]进行近似描述。假设叠前角道集中入射角为θ的地震道表示为s_θ(t)。对应的,入射角为θ的反射系数序列可以表示为r_θ(t),不同角度的地震子波表示为W_θ(t),则有如下的褶积模型表达式:

(7)

s_{θ} (t) = W_{θ} (t) * r_{θ} (t),

将式(7)写为式(6)的形式:

(8)

\begin{array}{l} s_{θ} (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{m = 1}} {a_{m, n, θ} w_{θ} (t) \times r_{e} (t, m, n, Δ t) + \\ b_{m, n, θ} w_{θ} (t) \times r_{o} (t, m, n, Δ t)}, \end{array}

式(8)即为叠前道集的奇偶分解公式。

常规反演中通过式(8)建立如下的目标函数:

(9)

O = ‖ s_{θ} - {\dot{s}}_{θ} ‖_{2}^{2},

式中: ${\dot{s}}_{θ}$ 表示实际叠前角道集,s_θ表示叠前角道集的奇偶子波分解,下标2表示向量的L₂范数。

常规反演算法都是在最小二乘意义下,使式(9)中的目标函数O达到最小时的系数a和b即为所求。本文基追踪算法(BP)建立的目标函数如式(10)所示:

(10)

O = ‖ s_{θ} - {\dot{s}}_{θ} ‖_{2}^{2} + λ ‖ r_{θ} ‖_{1},

式中:下标1表示向量的L₁范数,λ为调节因子。式(10)表示在反射系数L₁范数最小的条件下,当O→最小时的系数a和b即为所求。关于式(10)的求解算法文献中做了较为详细的论述^[13,14,15],本文对该算法不做赘述。当得到最佳系数a_m_,_n_,_θ和b_m_,_n_,_θ后,代入式(11)即可得不同角度的反射系数r_θ(t):

(11)

\begin{array}{l} r_{θ} (t) = \overset{N}{\sum_{n = 1}} \overset{M}{\sum_{m = 1}} {a_{m, n, θ} r_{e} (t, m, n, Δ t) + \\ b_{m, n, θ} r_{o} (t, m, n, Δ t)} 。 \end{array}

由Connolly公式可得弹性阻抗EI(θ)与反射系数序列之间的关系^[1]:

(12)

r_{θ} (t) = \frac{\partial}{\partial t} \ln EI (θ, t),

式(12)两端同时取积分得:

(13)

\ln [EI (θ, t)] = \int r_{θ} (t) d t,

进而得到公式:

(14)

EI (θ, t) = \exp [\int r_{θ} (t) d t] 。

式(14)为弹性阻抗计算公式,当θ=0时弹性阻抗等于声波阻抗^[1]。

2 合成数据试算

2.1 简单层状模型合成信号试算

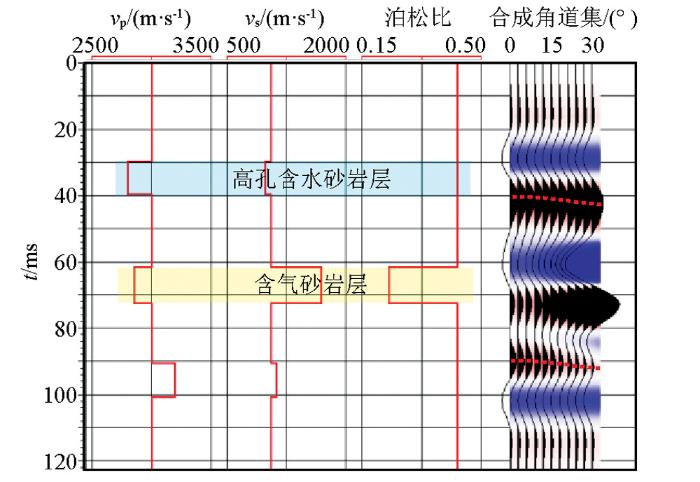
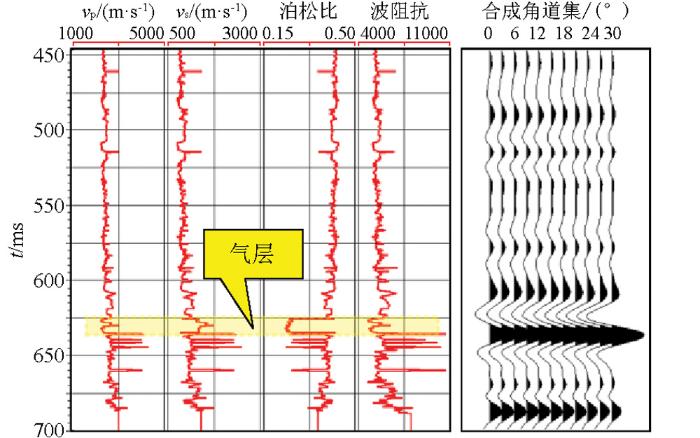
图2为一维层状模型及其叠前角道集合成记录,所用子波为主频30 Hz的零相位雷克子波,模型参数选取参考了Goodway模型。从图中可以看出,气层表现为低纵波速度、低泊松比特性,高孔水层的纵波速度更低,但泊松比较高。这里需要指出的是泊松比的反演不属于叠前弹性反演的范畴,而属于叠前同时反演。由于水层的孔隙度高,导致纵波速度比气层低,在叠后声波阻抗反演结果上无法对二者进行有效区分,必须借助弹性阻抗反演结果。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 模型及叠前正演道集

Fig.2 Model and pre-stack synthetic record

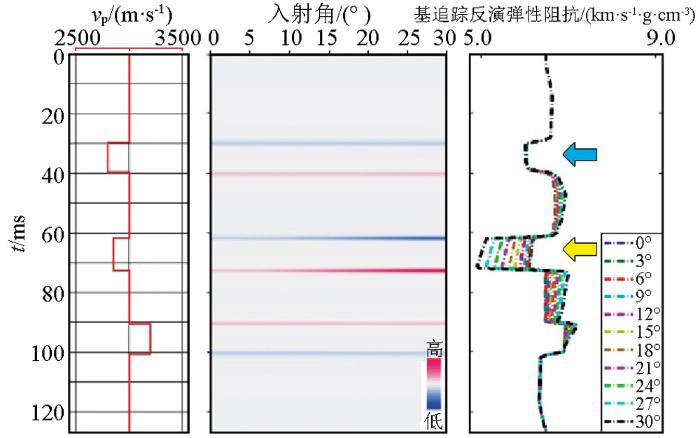
图3为利用图2中叠前道集进行的基追踪弹性反演结果,可以看出,水层弹性阻抗(蓝色箭头处)随入射角基本没有变化,而气层弹性阻抗(黄色箭头处)随入射角的增大显著降低,气层大角度弹性阻抗值明显低于高孔水层。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 对应图2中叠前道集的基追踪弹性反演

Fig.3 Elastic inversion result of pre-stack record in Fig.2

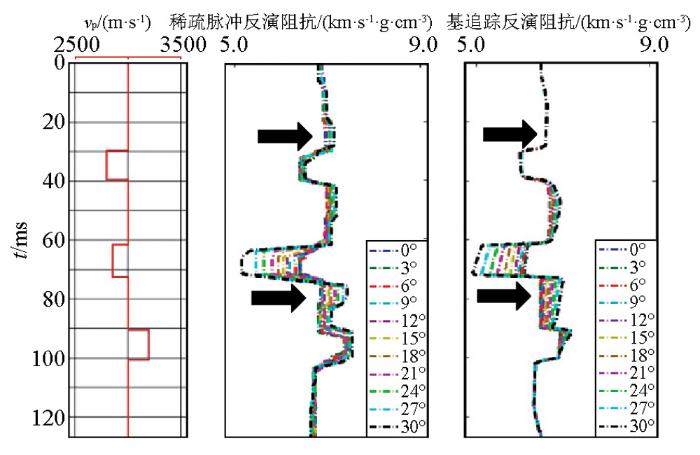
图4为传统稀疏脉冲反演结果和基追踪反演结果的比较,从图中可以看出,稀疏脉冲反演结果在水层和气层处也有类似于基追踪弹性阻抗的结果,但是在黑色箭头所示的位置稀疏脉冲反演结果在大角度时产生了明显的“假层”。产生这种现象的原因是图2中叠前角道集波峰和波谷的位置随着角度不同而发生移动(图2中红色虚线为波峰的位置),追踪峰谷所得的初始模型对于大角度道集误差较大,使得反演过程中大角度结果出现了明显“假层”。但是本文基追踪弹性反演算法所得的弹性阻抗在近角和远角所揭示的层位信息都十分稳定,没有“假层”出现。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 基追踪反演与稀疏脉冲反演结果比较

Fig.4 Comparison between SSI and BPI results

2.2 实际测井数据合成信号试算

图5是对实际井资料进行的叠前正演模拟。右侧道集为通过Zoeppritz方程人工合成的叠前角道集,入射角为0°~30°,地震子波为30 Hz的零相位雷克子波。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 实际井的叠前正演

Fig.5 Pre-stack simulation using a well data

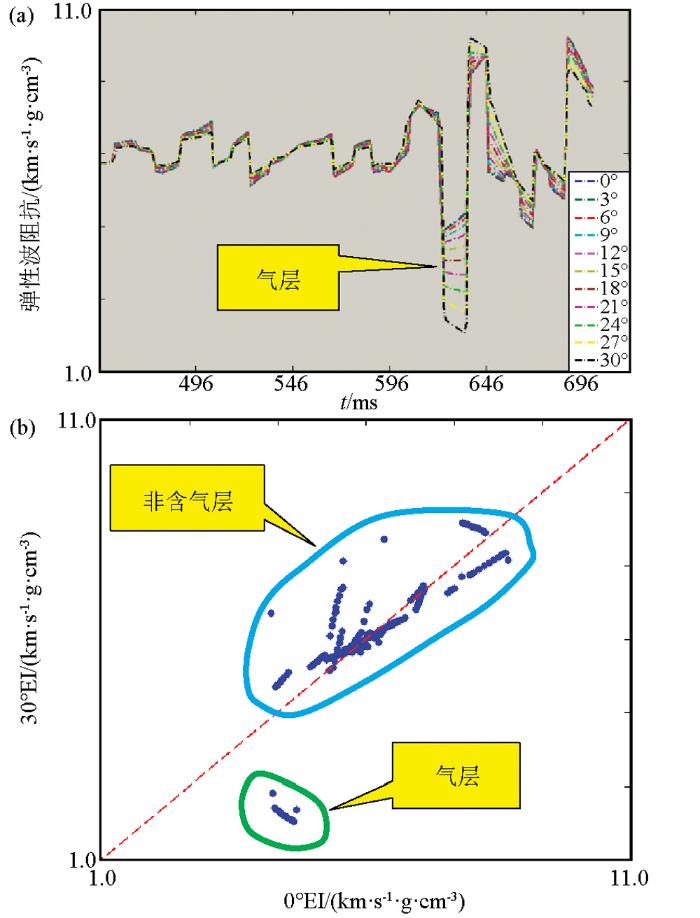
图6a为基追踪叠前弹性阻抗反演结果,从图中可以看出,随着角度的增大气层弹性阻抗明显呈现快速降低的趋势,而非含气层弹性阻抗变化不大。图6b为0°EI和30°EI的交会图,红色虚线为坐标系的对角线。从图中可以看出,含气层(绿色虚线)处在对角线下方,说明大角度弹性阻抗明显小于小角度弹性阻抗;非含气层(蓝色虚线)集中在对角线附近,说明小角度和大角度弹性阻抗明相差不大。据此规律可以识别含气储层的空间分布,其具体原理Connolly已经做了较详细的说明^[1],在此不再赘述。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 对应图5中合成道集的基追踪弹性反演

a—基追踪EI反演结果;b—0°EI与30°EI交会图

Fig.6 BP EI value of the synthetic record in Fig.5

a—EI result of BP method;b—crossplot of 0° and 30° EI

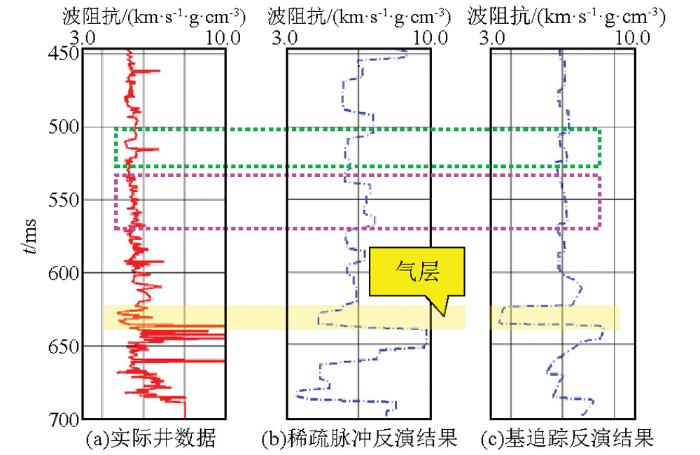
图7是对30°入射角的地震道进行稀疏脉冲反演与基追踪反演所得的结果对比。黄色阴影所示的层段为含气砂岩层段,稀疏脉冲反演结果与基追踪反演结果在此处都表现为明显的低阻异常。绿色虚线框所示的层段为一个低阻和高阻的互层,稀疏脉冲反演结果上表现为低阻层,无法对该层段进行识别,但基追踪反演曲线上可以较清楚地对该低阻和高阻互层进行识别。粉色虚线框所示的层段在实际测井曲线上表现为一套阻抗缓慢递增的韵律性地层,反映地层的压实程度随深度逐渐增高,是一套连续沉积的地层,稀疏脉冲反演结果显示该层为较均匀的高阻地层,与实测不符,而基追踪反演结果显示的规律与实际测井曲线的上述规律十分吻合。该例子进一步证明,基追踪反演方法对叠前大角度道集进行反演所得的结果比传统稀疏脉冲方法所得的结果更符合实际地层的沉积规律,有助于对储层的精确预测和识别。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 30°入射角时基追踪反演与稀疏脉冲反演结果比较

Fig.7 The comparison between SSI and BPI results with 30° incident angle

3 方法应用

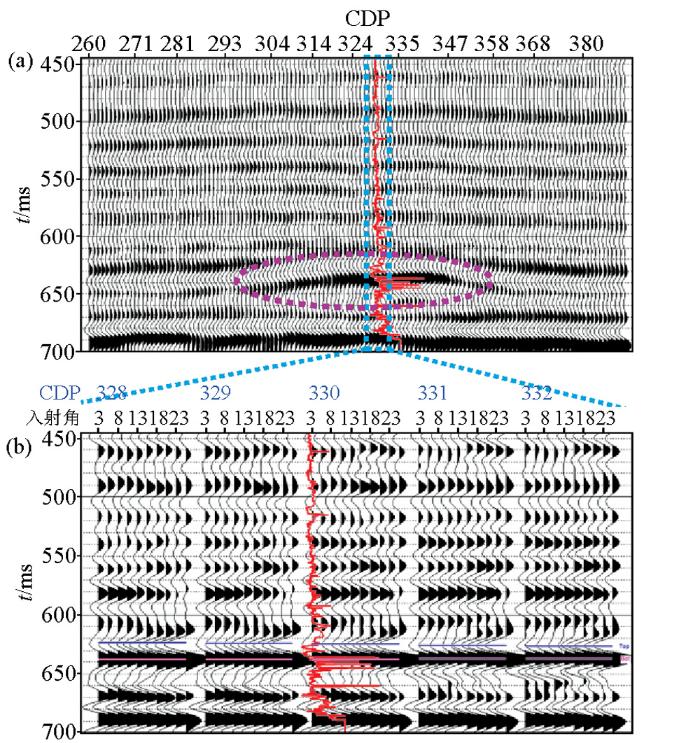
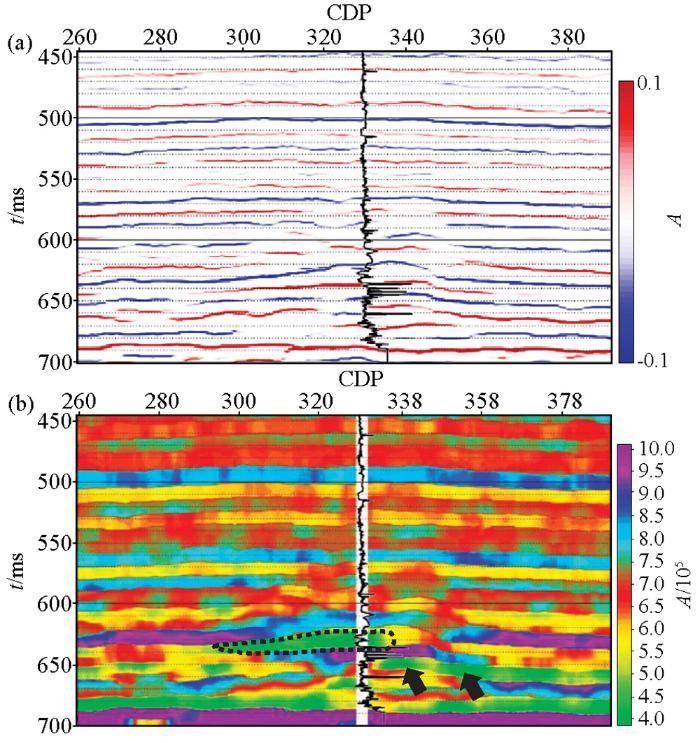
图8为Hampson-Russell软件中的DEMO数据,红色曲线为声阻抗测井曲线,图5和图7中该井含气砂岩储层位置已用黄色阴影标注。工区储层是固结程度较低的高孔隙度砂岩,且砂岩含气饱和度高(>50%),造成砂岩储层波阻抗小于上覆泥岩盖层,在叠后地震剖面上表现为“亮点”(粉色椭圆框内),叠后纵波剖面上的“亮点”解释可以有多种,例如图2中高孔含水砂岩层和含气砂岩层都可以形成“亮点”反射。因此,用叠后“亮点”特征对储层含气性进行评价多解性强。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 野外地震数据

a—叠后地震资料;b—基于CDP点处的叠前角道集

Fig.8 Field seismic data

a—poststack seismic data;b—prestack angular gathers based on CDP

图9为该区叠后地震资料的基追踪反演结果。图9a为反演所得的反射系数剖面,从图中可以看出,反射系数剖面具有很高的分辨率,井上反映的主要阻抗界面在反演剖面上都有所体现。图9b为对图9a中反射系数剖面进行道积分所得的叠后波阻抗剖面,在亮点位置得到明显的低阻异常(黑色虚线框内),如前所述,这不足以证明该“亮点”是由于砂岩储层含气引起的。黑色箭头处地层也是低阻异常,但钻井证实该地层为孔隙较发育的含水砂岩层。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 叠后基追踪反演结果

a—叠后基追踪反演反射系数剖面;b—叠后基追踪反演阻抗剖面

Fig.9 BPI results of post-stack seismic data

a—reflectivity inversion result of post-stack BPI;b—impedance inversion result of post-stack BPI

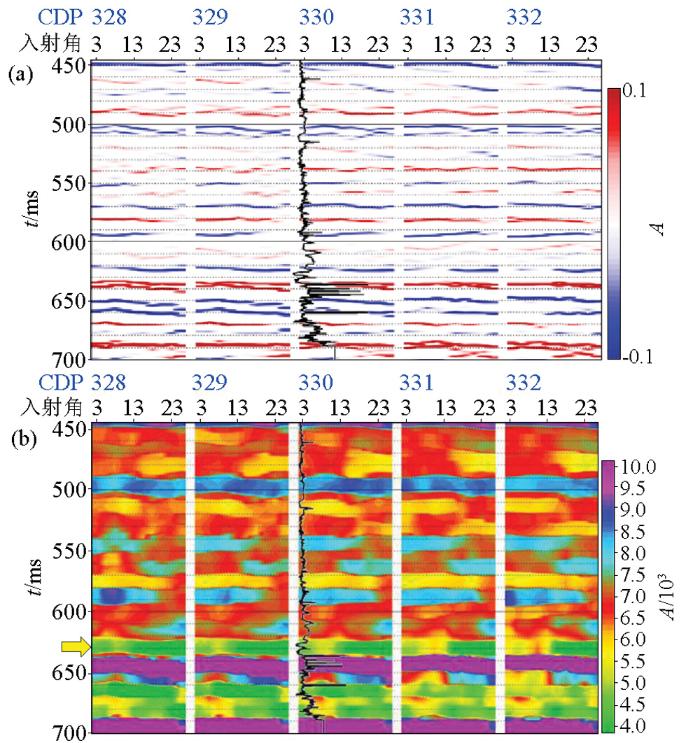
为了准确预测该区含气砂岩储层的分布,对其进行基追踪弹性反演。图10为对图8中叠前地震数据进行弹性反演的结果。图10a为对应角道集的反射系数剖面,由于叠前资料的信噪比较低,因此反演所得的反射系数剖面的信噪比低于叠后反射系数剖面(图9a)。图10b为利用式(14)所得的若干CDP点处的弹性阻抗剖面,从图中可以清楚地看出,相同地层不同入射角时的弹性阻抗均有所差异,特别是黄色箭头所示的砂岩储层,随着入射角的增大,弹性阻抗显著减小,这是砂岩储层含气后的显著特征^[1]。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 基追踪弹性反演结果

a—基追踪弹性反演反射系数剖面;b—基追踪弹性阻抗剖面

Fig.10 BPI elastic inversion results

a—reflectivity profile of elastic BPI;b—EI profile of BPI

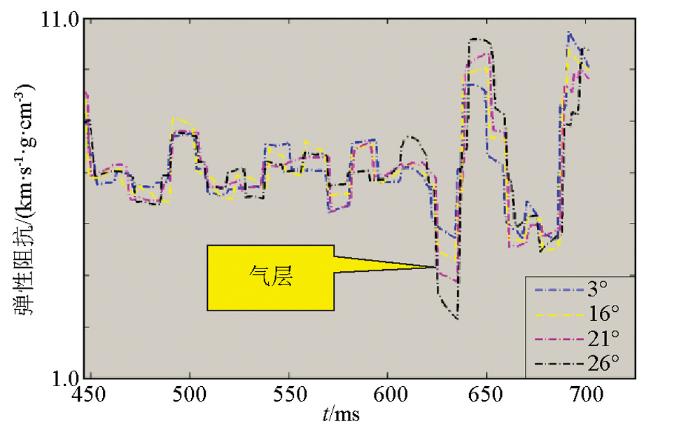
图11为若干不同角度井旁弹性阻抗反演结果,从图中可以看出,含气砂岩储层弹性阻抗随入射角度的增大而显著降低,其他非含气层段没有这种特征。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同入射角井旁弹性阻抗反演结果

Fig.11 Elastic inversion results with different incident angles near well location

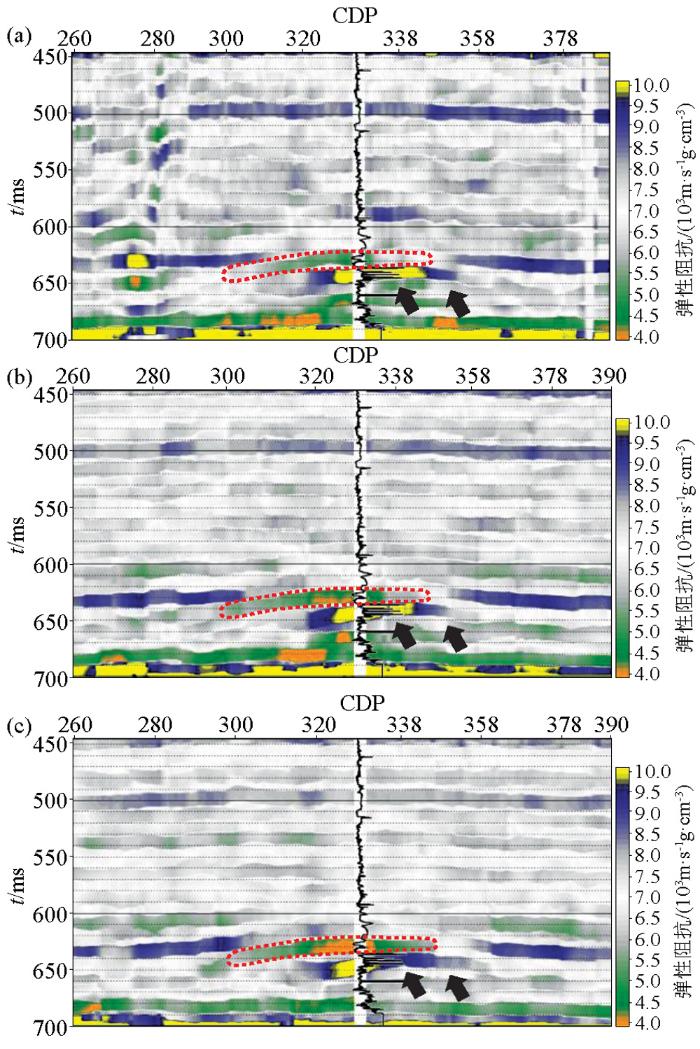
为进一步展示含气砂岩储层的横向分布特征,如图12所示分角度提取弹性阻抗剖面。对比三者可以发现,背斜顶部红色虚线框内砂岩储层的弹性阻抗随入射角度的增大逐渐降低,表明红色虚线框内为含气砂岩储层的实际分布范围。图9b叠后基追踪声阻抗反演剖面上除含气砂岩储层外,背斜圈闭内还存在低阻层(黑色箭头所示),在基追踪弹性反演剖面上的相应位置不具有弹性阻抗随入射角度逐渐降低的特性(图12中的黑色箭头所示),据此可以判断,叠后波阻抗剖面上的该低阻层不是由储层含气造成的。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同入射角的弹性阻抗剖面

a—3°弹性阻抗剖面;b—16°弹性阻抗剖面;c—26°弹性阻抗剖面

Fig.12 Elastic impedance profiles with different incident angles

a—3° EI profile;b—16° EI profile;c—26° EI profile

4 结论

本文将基追踪分解算法用于叠前弹性阻抗反演,相比于传统稀疏脉冲法,本文方法可以有效压制大角度弹性阻抗反演时较易出现的“假层”现象。

砂岩含气后或高孔含水砂岩都会表现为低波阻抗,有时高孔含水砂岩的阻抗会低于含气砂岩,叠后波阻抗反演无法对二者进行有效区分和识别。但含气砂岩储层在弹性阻抗剖面上表现出的特点是随着地震波入射角度的增大,弹性阻抗显著降低,而含水砂岩弹性阻抗随地震波入射角度变化不明显。利用这一性质,采用本文基追踪弹性阻抗反演方法对某区的含气砂岩储层的分布进行了预测,预测结果与钻井数据相吻合。与叠后声阻抗反演比较后发现,本文方法多解性低,在含气砂岩储层的分布预测中具有更高的应用价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Connolly

, Amoco B

Elastic impedance

[J]. The Leading Edge, 1999,18(4):438-452.

[本文引用: 5]

[2]

He F

, You

, Chen K

Gas sand distribution prediction by prestack elastic inversion based on rock physics modeling and analysis

[J]. Applied Geophysics, 2011,8(3):197-205.