0 引言
基于以上情况,本文从Maxwell方程出发,采用矢量位和标量位控制方程,以有限单元法为工具,对广域电磁法三维数值模拟方法进行了研究。为获得精确的三维数值解,文中采用库伦规范解决三维电磁法节点有限元数值模拟中电导率界面法向方向电场不连续问题,并对线性方程组的求解和广域视电阻率的计算进行了阐述。在模型算例中,首先采用具有解析解的均匀半空间模型对本文算法的计算精度进行了验证。然后,对大深度异常体模型进行了数值模拟研究,数值结果表明,广域电磁法具有探测深度大,计算精度高的特点。
1 方法理论
1.1 控制方程
频率域中Maxwell方程组可以表示为(谐变因子为负号,e-iwt):
式中:ε、μ、σ分别为介质的介电常数、磁导率和电导率,在真空中,ε0=8.85×10-12 F/m,μ0=4π×10-7 H/m;ω=2πfp,为角频率;fp为电磁波频率;电流J分解成为电流密度Js与传导电流σE以及位移电流-iωεE之和,表示电流来源于地层内部的感应电流和涡旋电流。对式(1a)两边取旋度并代入式(1b),消去磁场强度H得到关于电场的二阶矢量Helmholtz方程:
式中:A为矢量位;Φ为标量位;
1.2 有限单元法
对本文中矢量位和标量位控制方程采用加权余量法得:
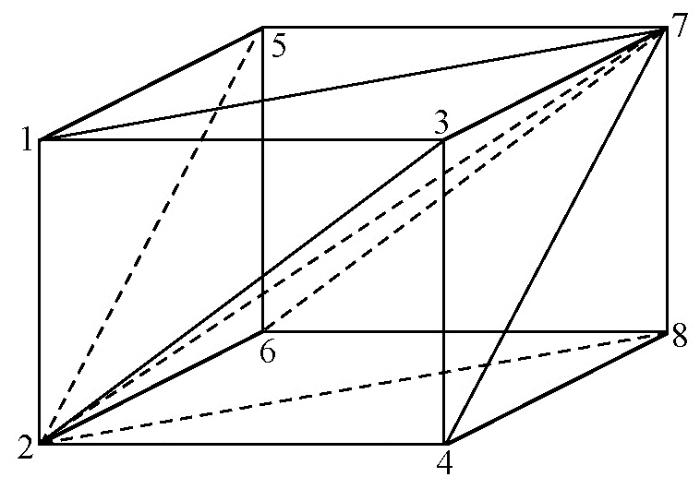
图1
网格插值基单元为四面体单元,采用线性插值函数(式(4)中二阶导数项采用格林函数进行),设u=a1x+a2y+a3z+a4是单元中的线性函数。根据四面体中4个顶点的坐标和函数值,可确定4个系数a1,…,a4。也可将线性函数写成:
式中,形函数Nj=Lj(j=1,…,4),三维自然坐标(或体积坐标)相关描述参见文献[21]。采用形函数对式(4)进行单元分析,然后合成得到总体系数矩阵。
1.3 线性方程组求解
采用有限单元法求解矢量位和标量位控制方程,经过单元分析,系数合成后得到大型稀疏复系数线性方程组:
式中:稀疏矩阵A为大型对称稀疏复系数矩阵,采用非零元存储(线性插值最大非零元个数为27),其维度为Na×27,Na为待求解未知量x的个数4Nx×Ny×Nz(Nx、Ny、Nz分别为x、y、z方向网格节点个数);B为右端项场源向量。
本文采用MKL库中Pardiso求解器对方程(6)进行求解,求解得到Ax、Ay、Az和Φ分量,再利用矢量位、标量位和电场之间的关系式求得电场Ex(广域电磁法只需要观测x方向电场分量)。
式中:标量位Φ的一阶偏导为空间导数,采用中心差分计算得到。
1.4 E-Ex广域视电阻率计算
为突破卡尼亚视电阻率所需“远区”的应用局限性,何继善[24]根据均匀半空间模型中电磁场表达式的特点,定义了广域视电阻率,将电磁测深范围扩大到包括“远区”的广大区域。E-Ex观测系统中,电偶极源激励的电场分量Ex对应的广域视电阻率:
式中:
式(8)中,由于
2 模型试算
模型试算中,首先采用具有解析解的均匀半空间模型对本文算法的正确性进行验证。然后通过两个模型对广域电磁法探测深度进行三维模拟研究。本文线性方程组求解均采用Pardiso直接解法求解器,测试电脑配置如下:联想Thinkpad P52移动工作站,内存128 GB,6核12线程,处理器为intel® CoreTM i7-8750 CPU @2.20GHz。
2.1 均匀半空间模型
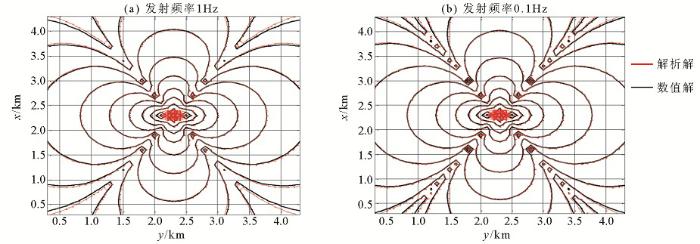
设计电阻率为100 Ω·m的均匀半空间模型,长导线场源沿x方向布设于地表中心,偶极距为200 m,发射电流幅值为50 A,发射频率分别为1 Hz(图2a)和0.1 Hz(图2b),模型网格剖分参数Nx×Ny×Nz为61×61×51,水平方向做均匀剖分,网格间距为100 m,垂向方向地表浅层网格间距为1 m,随着网格层数的增加网格间距增大,地下空间计算深度3 000 m,空气介质中计算高度5 000 m,水平方向各取5个节点作为扩边处理。如图2所示为地表电场Ex分量数值解和解析解重叠图,正演时间18 min,占用内存35 GB。从图中可以看出除零值线附近存在误差外,其他观测区域数值均误差低于1%,从而验证了本文算法的正确性。
图2
图2
地表Ex分量数值解与解析解对数重叠
Fig.2
Logarithmic superposition of numerical solution and analytical solution of surface Ex component
2.2 E-Ex观测系统大深度模型算例
2.2.1 浅层低阻异常体
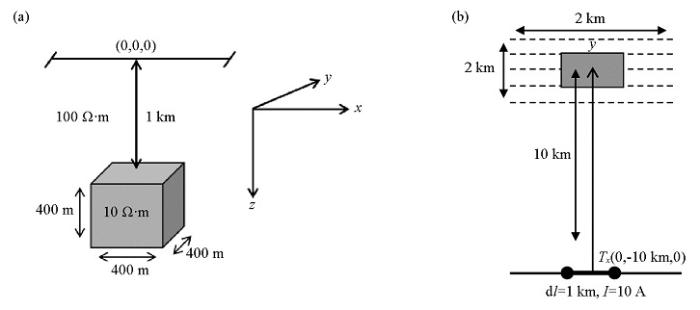
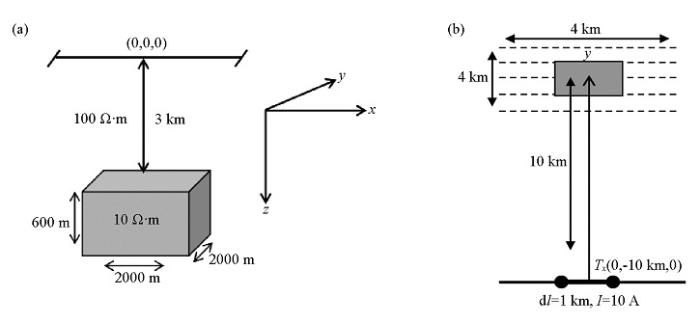
建立如图3所示地电模型和观测系统,在目标体正上方的地表布设20条测线,线距为100 m,每条测线上布设40个测点,点距为50 m。模型背景电阻率大小为100 Ω·m,低阻异常体为10 Ω·m,位于观测区域正下方,其长宽高分别为400 m×400 m×400 m,埋深深度为 1 000 m,发射场源长度为1 km,其中心点位于(0,-10 km,0)。
图3
图3
浅层地电模型(a)和观测系统示意(b)
Fig.3
Diagram of shallow geoelectric model(a) and observation system(b)
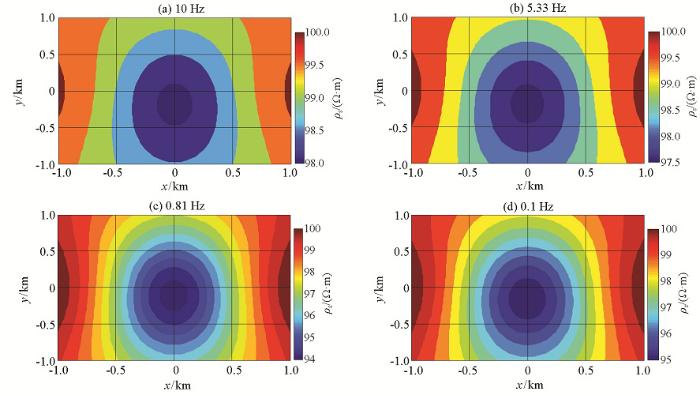
图4所示为不同频率广域视电阻率平面,分别展示了10、5.33、0.81和0.1 Hz,其最大异常幅度分别为2%、2.5%、6%和5%,当频率达到0.81 Hz附近异常最大。
图4
图4
浅层地电模型不同频率观测区域广域视电阻率分布
Fig.4
Distribution map of wide field apparent resistivity on observation areas with different frequency of shallow geoelectric model
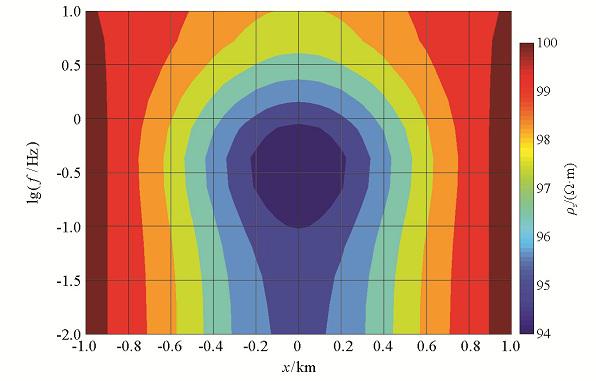
图5所示为y=0测线频率测点视电阻率组合剖面,在对数区间均匀等间隔选取12个频率进行计算,最高计算频率为10 Hz,最低计算频率0.1 Hz 。
图5
图5
浅层地电模型y=0测线频率组合剖面
Fig.5
Frequency combination profile with y=0 line of shallow geoelectric model
2.2.2 深部低阻异常体
图6
图6
深层地电模型(a)和观测系统示意(b)
Fig.6
Diagram of deep geoelectric model(a) and observation system(b) Sketch Map
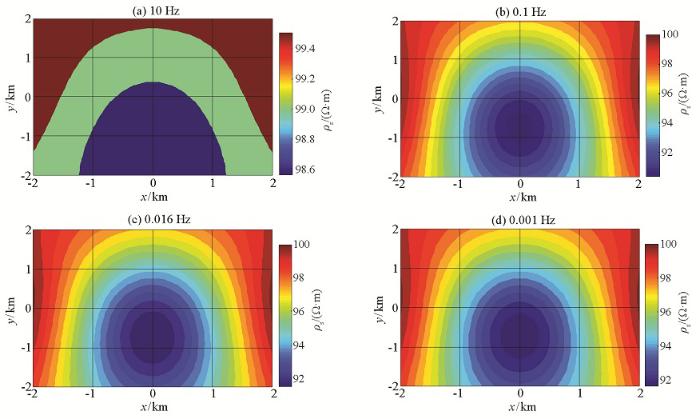
图7所示为深层地电模型广域电磁法三维正演计算结果,图中分别展示了10、0.1、0.016和0.001 Hz模拟结果。
图7
图7
深层模型不同频率观测区域广域视电阻率分布
Fig.7
Distribution map of wide field apparent resistivity on observation areas with different frequency of deep geoelectric model
图8
图8
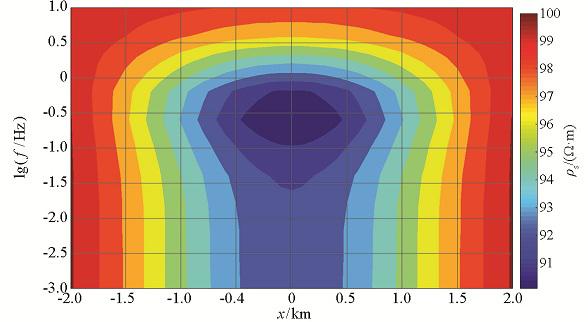
y=0测线频率组合剖面
Fig.8
Frequency combination profile with y=0 line of deep geoelectric model
3 结论及讨论
本文以有限单元法为工具,从基于频率域Maxwell方程基本理论出发,采用矢量位和标量位控制方程,对广域电磁法三维有限单元法数值模拟方法进行了研究。均匀半空间模型数值模拟结果验证了本文广域电磁法三维数值模拟的正确性,为后文数值模拟结果的分析与研究提供了数值计算工具。通过数值模拟结果进行分析可以得出如下结论:
1)当频率从高频到低频,测线位置从场源远区迈入中近区,其视电阻率剖面能清晰地反映地下异常体的信息,与传统CSAMT卡尼亚视电阻率相比,广域电磁法计算的广域视电阻率不受场源“中近区”的影响,可以在全区范围内进行测量,从而大大地拓展了广域电磁法观测区域。
2)当异常体顶界面埋深3km时,广域电磁法依然能够反映地下异常体的信息,从而证明了广域电磁法探测深度大的特性,从而为该方法在深地探测应用提供了理论支撑。
致谢
感谢广州电力设计研究院肖波、桂林理工大学张钱江副教授和湖南继善高科技有限公司田红军对本文提出的指导意见。
参考文献
大深度高精度广域电磁勘探理论与技术
[J].
Theory and technology of wide field electromagnetic method
[J].
广域电磁法在隐伏金矿中的应用
[J].
The application of wide-field electromagnetic method to hidden gold deposit
[J].
广域电磁法在湘西北页岩气探测中的应用
[J].将广域电磁法应用于湘西龙山地区的碳质页岩探测,揭示了该区碳质页岩的含碳量较高,相对上、下地层显示为低阻的特征。采用自主研发的“重磁电三维反演成像解释一体化系统”进行广域电磁法数据处理,获得了地下电性体真实的电阻率特征,基本查明龙山地区碳质泥页岩层位的电性分布规律。表明广域电磁法是获取碳质页岩分布范围和埋深的有效探测手段。
Shale gas detection with wide field electromagnetic method in North western Hunan
[J].
E-Ex广域电磁法三维数值模拟
[J].
Three-dimensional modeling for E-Ex wide field electromagnetic methods
[J].
广域电磁法在赣南某盆地油气勘探中的应用
[J].
Application of wide field electromagnetic method to the hydrocarbon exploration in a basin of South Jiangxi
[J].
用广域电磁法勘查深层地热资源
[J].
Exploration of deep geothermal energy resources with wide field electromagnetic method
[J].
广域电磁法在辽西地区牛营子凹陷油气资源潜力评价中的应用
[J].
The application of wide field electromagnetic method to the oil and gas exploration of Niuyingzi sag in Liaoxi area
[J].
Finite element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials
[J].DOI:10.1190/1.1444968 URL [本文引用: 4]
多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件
[J].
An approximate boundary condition for FEM-based 3-D numerical simulation with multi-source direct current resistivity method
[J].
Electromagnetic induction in a fully 3-D anisotropic earth
[J].DOI:10.1190/1.1500371 URL [本文引用: 1]
3D finite-difference frequency-domain modeling of controlled source electromagnetic data:Direct solution and optimization for high accuracy
[J].
Electromagnetic scattering of large structures in layered earths using integral equations
[J].DOI:10.1029/95RS00833 URL [本文引用: 1]
用积分方程法研究源与勘探区之间的三维体对CSAMT观测曲线的影响
[J].
DOI:10.3969/j.issn.0001-5733.2009.06.019
URL
[本文引用: 1]

在可控源音频大地电磁法野外作业中,源和勘探区间的距离可达几公里,为了了解源和勘探区间的异常体对勘探区内异常响应的影响,我们用三维压缩积分方程法做了数值模拟研究.首先对勘探区目标体进行了数值模拟,发现在高频时,观测到的异常中心位于目标体的正上方,随着频率降低,出现异常中心向远离源的方向略有移动的现象,所以对三维异常体最好用3D软件来解释.然后,对源和勘探区间存在三维异常体的情况进行了数值模拟与分析讨论.模拟结果表明只有当三维异常体达到较大的规模时,才会对目标体上方的观测曲线造成影响,否则其电阻率的变化及埋深的变化对观测曲线的影响较小,可以忽略.当异常体在源方向有延伸时,观测曲线受到的干扰最大,沿垂直源布设的方向延伸时引起的干扰中等,垂直地面向下延伸引起的干扰最小.]]>
Research on the effect of 3D body between transmitter and receivers on CSAMT response using Integral Equation method
[J].
基于二次耦合势的广域电磁法有限体积三维正演计算
[J].
3-D finite-volume forward modeling of wide-field EM using scattered potentials
[J].
三维空源电磁法非线性共轭梯度反演研究
[D].
Nonlinear conjugate gradient inversion of three-dimensional space-source electromagnetic method
[D].
Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver
[J].
DOI:10.1093/gji/ggt055
URL
[本文引用: 1]

For 3-D inversion of controlled-source electromagnetic (CSEM) data, increasing availability of high-performance computers enables us to apply inversion techniques that are theoretically favourable, yet have previously been considered to be computationally too demanding. We present a newly developed parallel distributed 3-D inversion algorithm for interpreting CSEM data in the frequency domain. Our scheme is based on a direct forward solver and uses Gauss Newton minimization with explicit formation of the Jacobian. This combination is advantageous, because Gauss Newton minimization converges rapidly, limiting the number of expensive forward modelling cycles. Explicit calculation of the Jacobian allows us to (i) precondition the Gauss Newton system, which further accelerates convergence, (ii) determine suitable regularization parameters by comparing matrix nouns of data-and model-dependent terms in the objective function and (iii) thoroughly analyse data sensitivities and interdependencies. We show that explicit Jacobian formation in combination with direct solvers is likely to require less memory than combinations of direct solvers and implicit Jacobian usage for many moderate-scale CSEM surveys. We demonstrate the excellent convergence properties of the new inversion scheme for several synthetic models. We compare model updates determined by solving either a system of normal equations or, alternatively, a linear least-squares system. We assess the behaviour of three different stabilizing functionals in the framework of our inversion scheme, and demonstrate that implicit regularization resulting from incomplete iterative solution of the model update equations helps stabilize the inversion. We show inversions of models with up to two million unknowns in the forward solution, which clearly demonstrates applicability of our approach to real-world problems.
复杂场源形态的海洋可控源电磁三维正演
[J].
DOI:10.6038/cjg20150330
URL
[本文引用: 2]

在使用电偶极发射源的可控源电磁法(CSEM)勘探中,发射源的方位、长度、形状等对观测数据有重要的影响,然而现有的大部分三维数值模拟方法没有全面地将这些因素考虑进来,很多都只能应对非常简单的场源形态,例如单一方位的点电偶极子,这有可能显著降低模拟结果的准确性.本文实现了基于交错网格有限体积(FV)离散的海洋CSEM三维正演算法,能够模拟形态相对复杂的场源,包括任意方位的有限长直导线和弯曲导线发射源.该算法使用一次场/二次场方法,只需对二次场使用FV法求解,避免了场源的奇异性问题;一次场的计算为一维正演问题,使用准解析法求解,并且只要在计算一次场时考虑复杂的场源形态便可以实现同样场源的三维正演.通过与一维理论模型的解析解对比验证了三维程序的准确性,并针对三维理论模型进行了一系列正演测试,初步考察了场源形态对三维正演结果的影响.
Three-dimensional forward modeling of the marine controlled-source electromagnetic field with complex source geometries
[J].
Coulomb 规范下地电磁场的自适应有限元模拟的理论分析
[J].地电磁场的直接求解法存在伪解现象,且电磁场分量在界面上的不连续性与节点型有限元的基本要求矛盾. 本文将Coulomb 规范下磁矢量势-电标量势与自适应有限元相结合,提出了地球物理电磁场计算的快速、高精度方法. 首先从地电磁场一般边值问题出发,给出了Coulomb 规范下磁矢量势-电标量势的公式系统,分析了求解域内势的连续性. 采用Galerkin 加权余值法推导出积分弱解形式和Delaunay非结构化四面体单元时Hierarchal 基函数的有限元方程. 基于超收敛恢复技术,提出了适用于电磁场的后验误差估计方法,阐述了地电磁场自适应计算的策略及迭代算法,分析了计算时间消耗和误差收敛性质,表明本文方法可以用最优的计算资源得到呈拟指数收敛到准确解的数值结果,从而为后续的数值计算奠定了理论基础. ]]>
Theoretical analysis of geo-electromagnetic modeling on Coulomb gauged potentials by adaptive finite element method
[J].
全区观测多次覆盖可控源电磁法观测系统模拟研究
[D].
The simulation study of whole range multi-fold CSEM observation system
[D].
三维海洋可控源电磁法矢量有限元与耦合势有限体积数值模拟
[D].
Numerical simulation of three-dimensional marine controllable source electromagnetic normal vector finite element and coupled potential finite volume
[D].
基于电场矢量波动方程的3D可控源电磁法有限单元法数值模拟
[J].
DOI:10.3969/j.issn.0001-5733.2009.12.023
URL
[本文引用: 1]

从可控源电磁法的基本原理出发,推导了基于电场矢量波动方程的三维边值问题,利用广义变分原理,把边值问题转换为变分问题,并引入散度条件,避免了伪解的出现,使有限元计算在理论上更加完备.在准静态近似条件下,把水平电偶极子在空中和大地的远区电场闭合表达式作为有限元计算中的区域外边界条件,解决了边界条件加载的困难;把应用于地震模拟中的伪delta函数引入到可控源电磁法中的三维有限元模拟中,消除了源点的奇异性,提高了方程组的稳定性.通过对均匀大地和层状介质模型的模拟,检验了程序的正确性,并对典型的地质体模型进行了数值模拟,分析了其变化规律.]]>
Three dimensional controlled source electromagnetic numerical simulation based on electric field vector wave equation using finite element method
[J].
耦合势有限体积法高效模拟各向异性地层中海洋可控源的三维电磁响应
[J].
DOI:10.7498/aps.63.159101
URL
[本文引用: 1]

本文基于电场矢势与标势分解的耦合势有限体积法研究建立一套各向异性地层中海洋可控源电磁法的三维响应的高效数值模拟技术. 首先引入电场的矢势和标势,将电场分解为无散场和无旋场之和,Maxwell方程转换为关于矢势与标势的混合Helmholtz方程,克服低感应数问题. 在此基础上,借助Yee氏交错网格和有限体积法以及非均质单元中等效电导率公式,建立混合Helmholtz方程的离散方程. 并采用直接法求解器PARDISO求解离散方程,有效保证在大的求解空间中仍然能够获得电磁场稳定可靠的数值解. 此外,在数值模拟中利用差异场技术,克服源的奇异性问题,尽可能提高近场的计算精度. 与解析解的对比证明了该算法的有效性. 数值模拟结果表明,海洋可控源电磁法沿测线方向的电场,对油气藏的纵向电阻率敏感,对横向电阻率不敏感;对油气藏上方的覆盖层的纵向电阻率和横向电阻率都敏感.
Efficient simulation of three-dimensional marine controlled-source electromagnetic response in anisotropic formation by means of coupled potential finite volume method
[J].
DOI:10.7498/aps.63.159101
URL
[本文引用: 1]

A coupled potential finite volume method for simulation of three-dimensional marine controlled-source electromagnetic (CSEM) response in anisotropic formation is developed. To circumvent ill-conditioning and convergence problems, Maxwell's equations are reformulated into coupled scalar-vector potentials with Coulomb gauge and its complement by applying a Helmholtz decomposition to the electric field. Yee's staggered girds, finite volume averaging and interpolation techniques are used to make the Helmholtz equations discrete. The resulting sparse and complex linear system in large-scale models is solved by a direct solver PARDISO. In order to improve the accuracy of the near field results without significantly reducing the computational efficiency, a method using difference fields is proposed to reduce the source singularity effect of anisotropic formation. The anisotropic modeling examples show that marine CSEM response is predominantly sensitive to reservoir vertical resistivity, not to reservoir horizontal resistivity, provided that the reservoir are thin and high-resistive; but the marine CSEM response is sensitive to both horizontal and vertical resistivity of the overburden on top of the reservoir.