0 引言
旋回地层学(Cyclostratigraphy)是指对地层记录的(准)周期性旋回变化进行识别、描述、对比和成因解释,并将其应用于地质年代学以提高年代地层框架的精度和分辨率,实现地层高精度划分与对比的一门地层学分支学科,其中一项重要的工作就是划分地层层序和研究沉积相,而沉积旋回是沉积相的一个重要标志[1-2]。在沉积旋回划分上前人多基于测井资料,这种方法对井点处的沉积旋回划分较准确,但其研究范围局限性较大,在工区内井点较少的情况下,通过地质规律从井点处外推,无法得到相对准确的沉积旋回划分结果。地震数据作为地层岩性、物性的反映,蕴含了大量与沉积旋回有关的信息,然而直接利用地震资料来进行沉积旋回划分的方法垂向分辨率较低,划分不够精确[3]。随着信号分析技术的发展,时频分析技术逐渐成为研究地层旋回性的重要方法,目前应用于旋回识别的时频分析方法很多,包括傅里叶变换、小波分析、广义S变换以及Wigner-Ville分布等方法[4-14]。地震信号是一种具有短时、突变等特点的典型非平稳随机信号,短时傅立叶变换、小波变换和S变换等由于受到分辨率和信号平稳性的限制,影响了其利用地震信号进行地层沉积旋回判别的精度[15-17]。
Wigner-Ville分布是一种二次型时频分析方法,相比于傅里叶变换等单线性时频分析方法,Wigner-Ville分布避免了线性时频分析中时间分辨率和频率分辨率的互相牵制[13],分辨率较高,但由于其受到交叉项干扰的影响严重[9,14],因而难以判断旋回模式。affine类时频分布(尺度图)通过affine平滑来抑制交叉项,它能够有效地抑制交叉项带来的影响,该方法通过对频谱的平滑,模糊了瞬时频谱变化细节,突出了主要频率的变化趋势[18],具有较好的沉积旋回判别能力。基于affine类时频分布的旋回性薄互层时频特征有向层厚减薄方向的升频特点,为探索这一规律是否适用于所有情况,本文以正旋回模型为基础,通过改变旋回模型内部小层厚度、地层波阻抗大小、噪声强度、地震资料频率、地层黏性大小等5个影响因素,利用深度域相移法对不同影响因素条件下的模型进行正演模拟,抽取零偏移距道集进行仿射类时频分析,与理想情况下正旋回模型仿射类时频特征进行对比,研究该方法的适用性。
1 Affine类时频分析基本原理
式中,a为伸缩尺度,t为时间变量,ξ、ν为频率变量,Wψ(t,ν)为任意平滑函数,Wx(s,ξ)是地震信号z(t)的wigner-ville变换。该分布函数也能保护信号能量,前提是Wψ(t,ν)满足:
这种表示定义了仿射类时频分布,仿射类时频分布是一种通过时移和伸缩变换实现的时频能量分布函数。从式(1)可见,很明显,Wigner-Ville分布是仿射类时频分布的组成部分:如果我们引入任意一非零频率ν0,并通过频率的倒转确定其尺度:
因为
故Wigner-Ville分布(WVD)相当于仿射类的一种元素。
式(1)的一个结果是,可将仿射类时频分布中元素的选择减少为仿射相关核的选择。当Wψ为二维的低通函数,其起到仿射平滑函数的作用,可减少由WVD所产生的干扰项。
尺度图对应于affine类时频分布中的
式中:z(t)为地震信号,b为平移因子(时间),h*(t)为小波母函数。式(2)对应仿射类时频分布式(1)中平滑函数Wψ。
2 地质模型设计与正演模拟
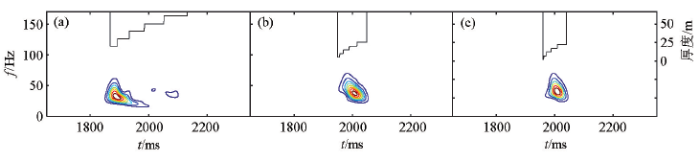
图1
图1
典型的正旋回模式仿射类时频分布
Fig.1
Typical affine time-frequency distributions of positive cyclic mode
正演实验参数除在探究地层波阻抗的变化对时频分布的影响时改变了速度参数,在探究地震资料主频变化对时频分布的影响时改变了地震资料主频参数,在探究地层黏性吸收参数Q值的变化对时频分布的影响时改变了黏性吸收参数以外,其余模型岩石物理参数为:砂岩速度2 918 m·s-1,密度2.14g·cm-3;泥岩速度3 180 m·s-1,密度2.32g·cm-3。计算出的反射系数大小均为0.084,相邻反射层极性相反。确立好岩石物理参数及地质模型后,采用零相位雷克子波作为地震子波,其主频39 Hz(峰值频率为30 Hz);基于波场延拓理论,采用深度域相移法正演模拟获取单炮记录;采取中间放炮、两边接收的采集方式,地震道采样点数为4 000,采样间隔为0.001 s,道间距为10 m,共1 000道。抽取零偏移距位置地震道进行affine类时频分析得到时频谱。
图1为典型的正旋回地层仿射类时频分布。正旋回随着深度增加,沉积物粒度逐渐变大,地层厚度逐渐相应增大。由图可见:正旋回,在仿射类时频分布图表现为随深度增加频率减小、振幅减弱、能量团减弱。基于此规律,文中对互层内小层厚度随机变化、地层波阻抗变化、背景噪声能量强度变化、地震资料主频变化、地层黏性吸收系数Q值变化等5个因素对旋回性薄互层时频特征的影响进行了研究。
3 影响因素分析
3.1 不同互层内小层厚度随机变化
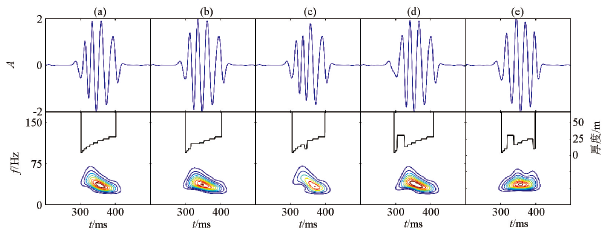
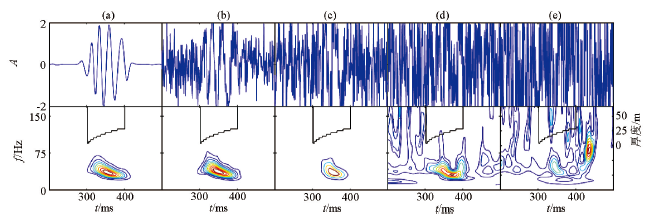
图2
图2
正旋回背景下内部某小层厚度随机变化时域波形及时频分布
Fig.2
Time domain waveforms and time-frequency distributions of random variation of inner layer thickness in positive cycle background
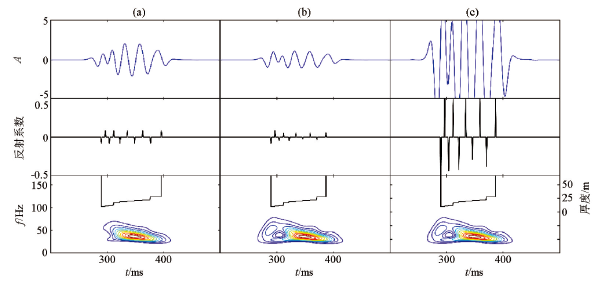
图3
图3
厚度相同改变反射系数后时域波形及时频分布
Fig.3
Time domain waveforms and time-frequency distributions after change of reflection coefficient with same thickness
对比小层厚度小幅调整的图2b、c、d与标准正韵律图2a,可以看出在模型略微不符合总体正韵律厚度变化的位置,时域波形及时频分布图上会有相应的响应,但对总体趋势影响并不大,时频分布图倾斜方向依然清晰并且容易判别出旋回类型。图2b第4、第5小层厚度突变,大于图2a,可以看出图2b时域波形在相应位置变稀疏但振幅能量增强,对应时频分布图相应位置向低频方向移动。图2c第6层厚度突然减薄,其时域波形在相应位置变密集且振幅减小,时频分布图在相应的位置频率有所升高。图2d第3层厚度突然变大,类似于一个薄互层与小的旋回体的组合,相应位置时域波形变稀疏振幅增强,时频分布图上相应位置向低频方向移动,整个频谱能量对应在小旋回体位置处。图2e第4层突然增大第9层减小,突变厚度接近整体30%,由于其突变位置为模型最底部一层,由于厚度突变处薄层的“升频降幅”作用,导致从整体来看波峰间距趋于均匀,相应的时频分布图已不具倾斜特征且趋于水平状,在模型薄层对应处频率有所升高。在时域波形上可以看出相对于图2d其时域波形原本稀疏的位置变得密集。
综上所述:在韵律背景下,若局部存在不符合韵律的轻微突变,affine类时频分布判别旋回模式的方法是适用的。但当突变厚度占总体厚度过大时,使用仿射类时频分布的方法难以区分韵律类型,而对应的这种地层模型也基本上脱离了韵律定义范畴。
3.2 波阻抗变化
图4
综上所述,波阻抗的变化对判别准则的影响较小,其主要改变频谱的时间方向的能量分布,对于频率方向影响较小。
3.3 加噪声分析
图5
图5
不同噪声强度的时域波形及时频分布
Fig.5
Time-domain waveforms and time-frequency distributions of different noise intensities
从图5可以观察到,时域波形从左到右噪声能量依次加强,当噪声能量达到-5 dB(图5c)时有效信号几乎完全淹没在噪声当中无法分辨,但时频分布整体特征与不加噪声情况依然相同,为明显的正旋回特征。随着噪声能量的加强,时频分布上的干扰越来越严重,当噪声能量增大到-9 dB(图5d),时域波形已经完全无法分辨,噪声能量几乎将时频分布特征完全淹没,但该噪声条件下时频分布图仍然残留一些正旋回特征,当噪声能量增大到-13 dB(图5e),由于噪声干扰过强,噪声的能量级别已高于子波的能量级别,时频分布图很难判别旋回性,但是这样的噪声情况在地震勘探中也是非常少见的。综上,可以看出正常噪声能量几乎不影响旋回判别,说明该方法抗噪性能良好。
3.4 地震资料频率变化
针对地震资料频率变化,设计地层模型同图6a,保持模型不变,改变地震资料峰值频率,探究峰值频率分别为20、30、40、50 Hz的频谱响应。
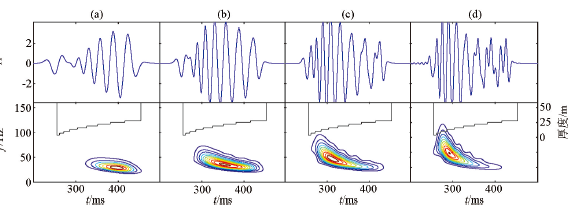
图6
图6
不同主频地震资料的时域波形及时频分布
Fig.6
Time-domain waveforms and time-frequency distributions of seismic data with different main frequencies
由图6可观察到,仿射类时频分布图上的正旋回特征随着地震资料主频的升高逐渐明显,观察图6a,由于峰值频率为20 Hz的地震资料主频较低,13 m以下的薄层区分效果很差,导致时域波形薄层对应位置处振幅较弱、波形稀疏,时频分布上旋回顶部薄层对应的能量较弱,时频分布整体对应在旋回中下部,且旋回特征较弱。图6b中旋回顶部薄层对应的时域波形能量明显增强,频域能量团对应位置也整体向旋回顶部移动,旋回的趋势也更加明显。观察图6c、d,地震资料主频更高,相比于图6a,子波干涉逐渐减轻,时域波峰数量增多,波形逐渐可分。在时频分布图上,正旋回特征较之图6b更加明显。另外观察图6c、d的时频分布图,频谱能量团在模型底部厚度变化位置处出现微小凸起,这是由于地震资料频率足够大,分辨率足够高引起的,对旋回性薄互层的内部结构精细判别具有一定的指导意义。
综上,基于仿射类时频分布判别地层旋回性受地震资料频率影响较小,且地震资料主频越大、峰值频率越高,旋回判别效果越好,对细节描述更精细。
3.5 地层黏性变化
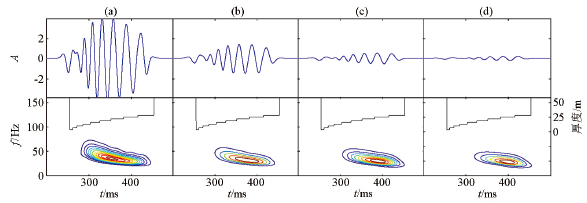
图7
图7
不同黏性地层的时域波形及时频分布
Fig.7
Time-domain waveforms and time-frequency distributions of different viscous formations
地下介质的黏性吸收作用会造成地震波时域波形发生扭曲,振幅减弱,频域高频能量损失。由图7可以观察到,时域波形从左到右能量依次衰减,时频分布图上能量团整体向低频区移动。相比于无黏性吸收的情况,图7b、c的弱、中黏性吸收地层的仿射类时频分布上依旧为倾向清晰的正旋回特征。当地层黏性Q值为66,时域波形振幅能量相比于图7a弱了一个数量级别,波形也发生了严重的畸变,从时域波形很难判别旋回的类型,但时频分布图上依然可以观察到比较明显的正旋回特征。另外观察图7的频域分布,在时间方向上,随着地层黏性的增强,薄层的“升频降幅”作用以及黏性吸收地层对高频的严重衰减作用也逐渐增强,因而时频分布主体逐渐移动,向旋回底部对应。
综上所述,在黏性吸收无、弱、中、强4种情况下,基于仿射类时频分布方法皆可对旋回进行有效判别,说明判别准则受地层黏性吸收作用的影响较小。
4 结论
1)旋回性薄互层内小层厚度轻微突变不影响频谱整体变化趋势,此时判别方法适用。但当突变厚度超过整体的30%时无法识别旋回模式,而此种薄互层也超出了旋回地层的定义范畴,因此,当地层旋回模式无法识别时,可以据此详细探究薄互层内部是否存在较厚小层。波阻抗变化对频率方向能量分布影响甚微,主要改变频谱时间方向的能量分布。
2)地震资料主频以及地层黏性的变化会造成分辨率的变化,随着地震主频的降低或者地层黏性的增大,地层分辨率会逐渐降低,对仿射类时频分布旋回判别准有一定的影响,但影响较小。在进行地层旋回性判别时,若地震资料主频较低或地层黏性较大,需要做好地震资料升频处理及地层黏性吸收补偿以达到更准确的效果。
3)正常能量噪声对仿射时频分布影响小,几乎不影响旋回模式判别,该方法抗噪性能良好,在地震资料噪声干扰较强时,依然可利用“时频谱向厚度减薄方向的升频现象”这一规律来判别旋回模式。
参考文献
旋回性沉积序列的形成机理分析
[J].
Analysis on the formational mechanism of depositional cycles
[J].
旋回地层——一个正在发展中的理论
[J].
Cyclostratigraphy: a developing theory
[J].
地震旋回体的概念及应用
[J].
Concept and application of seismic cycle characteristics
.[J].
时频分析方法在储层预测中的应用
[J].
Time frequency analysis method and its application in reservoir predicting
[J].
时频分析——薄互层结构研究的新途径
[J].
Time-frequency analysis—A new way for thin interbeds examination
[J].
High-frequency sequences and their stacking patterns:sequence-stratigraphic evidence of high-frequency eustatic cycles
[J].
时频分析及在地震信号分析中的应用研究
[D].
Time-frequency analysis and its implication in seismic signal
[D].
小波变换时频能量谱技术在地震地层划分中的应用
[J].
The time-frequency spectrum of wavelet transformand its application in seismic sequence identification
[J].
在小波时频域中研究沉积旋回
[J].
Study of sedimentary cycles in time-frequency domain of wavelet
[J].
Localization of the complex spectrum:the Stransform
[J].
基于广义S变换研究地震地层特征
[J].
Study on characteristics of seismic stratigraphyby generalized S-transform
[J].
基于广义S变换的沉积旋回分析方法研究
[J].
Study of sedimentary cycle analysis method based on generalized Stransform
[J].
希尔伯特——黄变换时频分析在沉积旋回划分中的应用
[J].
Application of Hilbert-Huang transform in sedimentary cycles classification
[J].
地震勘探信号时频分析方法对比与应用分析
[J].
The comparison and application analysis of time-frequency analysis method to seismic signals
[J].
线性时频分析方法综述
[J].
Review on linear time-frequency analysis methods
[J].
几种时频分析方法在沉积旋回判别效果上的对比
[J].
Comparison result of several time-frequency analysis methods on identifying sedimentary cycle
[J].
几种时频分析方法比较
[J].
The comparison of some time frequency analysis methods
[J].
时频分布中交叉项抑制的研究进展
[J].
Development of suppressing crossterms of time-frequency distribution
[J].
时频分析:回溯与前瞻
[J].
Which time-frequency analysis—A survey
[J].
Time-frequency analysis:Theory and application
[M].