基于程函方程的克希霍夫全平面域偏移成像方法

doi:10.11720/wtyht.2020.1319

基于程函方程的克希霍夫全平面域偏移成像方法

智敏^,, 朱建刚

中煤科工集团西安研究院有限公司,陕西西安 710077

Kirchhoff full plane imaging method based on Eikonal equation

ZHI Min^,, ZHU Jian-Gang

Xi'an Research Institute of China Coal Technology & Engineering Group,Xi'an 710077,China

责任编辑: 叶佩

收稿日期: 2019-06-24 修回日期: 2020-03-24 网络出版日期: 2020-08-20

基金资助:

国家重点研发计划课题“井下随掘巷道地质异常体动态探测技术与装备”. 2018YFC0807804
贵州省科技重大专项“薄煤层无人/少人采掘系统研究与应用示范”. [2018]3003-1

Received: 2019-06-24 Revised: 2020-03-24 Online: 2020-08-20

作者简介 About authors

智敏(1984-),男,汉族,江苏盐城人,2011年毕业于煤炭科学研究总院地球探测与信息技术专业,主要从事地震资料处理方面的研究工作。Email:zhimin@cctegxian.com

摘要

本文分别以直射线和弯曲射线初至波层析反演技术重建的速度为偏移速度,采用波前扩展外推方式求解程函方程,求取了成像区域内各节点初至波时间场,应用克希霍夫积分偏移技术对复杂模型叠前数据进行全平面偏移成像,成像结果表明:弯曲射线层析反演方法获得的速度场较直射线层析结果对速度异常体的刻画更准确,以弯曲射线层析反演速度场作为偏移速度可以获得较好的偏移成像结果。

关键词： 程函方程 ; 克希霍夫积分法 ; 全平面偏移成像 ; 弯曲射线层析反演 ; 直射线层析反演

Abstract

In this paper,the first arrival wave time field of imaging area is obtained by solving the Eikonal equation by using wavefront expansion extrapolation method.The full plane migration imaging of prestack data of complex model is performed by using Kirchhoff integral migration technique.The imaging results show that the inversion method of curve ray tomography describes the anomaly velocity body more accurately than straight ray tomography result.Better migration imaging results can be obtained by using the velocity field inverted by curved ray tomography.

Keywords： Eikonal equation ; Kirchhoff integral method ; full plane migration ; curve ray tomography ; straight ray tomography

PDF (3088KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

智敏, 朱建刚. 基于程函方程的克希霍夫全平面域偏移成像方法. 物探与化探[J], 2020, 44(4): 756-762 doi:10.11720/wtyht.2020.1319

ZHI Min, ZHU Jian-Gang. Kirchhoff full plane imaging method based on Eikonal equation. Geophysical and Geochemical Exploration[J], 2020, 44(4): 756-762 doi:10.11720/wtyht.2020.1319

0 引言

克希霍夫积分偏移是一种基于波动方程积分解的偏移成像方法,与其他偏移方法相比,该方法能够适应非规则观测系统,具有较高的计算效率^[1]。目前主流处理系统的克希霍夫偏移模块主要针对于地面地震数据成像,要求炮检点均位于地表,波场信息来自地下半空间,属于半空间成像方法。对于某些特殊地震观测系统,如煤矿井下槽波观测系统,地震信号可能来自以炮检点为焦点的完整椭圆上,属于全平面域偏移成像,主流处理软件并不适用。王季、姬广忠等基于直射线层析重构的槽波速度场,采用直射线克希霍夫积分偏移方法对井下反射槽波数据进行了偏移成像,取得了一定的效果^[23],该方法与地面地震直射线偏移成像一样,将绕射点与炮检点之间的射线路径视为直线,没有考虑速度场弯化引起的射线弯曲及旅行时变化,造成成像点与原绕射点不重合,降低了成像分辨率。

针对直射线层析成像速度的这一缺陷,本文采用弯曲射线层析成像方法反演成像区域速度。对于弯曲射线层析成像,射线追踪的精度直接影响着成像精度。常用的射线追踪方法有试射法、旅行时线性插值法(LTI)、快速步进法(FMM)、有限差分求解程函方程法。试射法对于简单速度模型具有较高精度,但不能处理折射波问题,对于复杂构造常存在追踪盲区,并且计算效率低下^[4]。LTI、FMM算法及有限差分法均首先计算从震源传至各节点的最小旅行时,并基于旅行时间采用反向追踪技术求取各检波点到炮点的射线路径。在计算最小旅行时时,LTI算法常采用按列(行)扫描的方式计算全局最小旅行时^[5],该方法未能考虑来自各个方向的射线,对于横向速度变化较大的介质,计算结果往往并非全局最小,叶佩等采用了全方位循环法求得了网格节点的全局最小旅行时^[6],张建中等采用Dijkstra算法逐点计算了各节点的最小旅行时^[7];FMM算法通过上风差分近似和窄带技术近似模拟地震波前的传播,具有计算精度高,运算速度快、无条件稳定的优点,可以计算网格节的全局最小旅行时,但该方法近源区域网格节点旅行计算误差较大,并对后续节点的计算精度有影响,需要对近源区的网格进行行加密处理,以提高近源区旅行时的计算精度^[8];有限差分求解程函方程法是一种计算精度高、运算量小的旅行时计算方法^[9],对于速度变化大的介质,采用传统的波前矩形扩展方可能因违返波传播的因果关系导致计算不稳定,潘纪顺等通过在算法中额外考虑首波、体波和散射波对旅行时影响的方式有效地解决了这一问题^[10]。本文采用有限差分法求解程函方程的方法求取成像平面内各节点的初至波旅行时场,算法上借鉴了潘纪顺的处理方法,波前扩展方法采用Disjkstra算法逐点计算各节点的全局最小旅行,射线反向追踪采用了Aldridge提出的最速下降法求取射线路径的方法^[11],并基于全局最小旅行时对二维复杂速度模型进行全平面域克希霍夫空间域偏移成像,通过对偏移结果的对比分析,认为该方法可以较真实地反映异常速度体的形态大小和位置,成像结果分辨率较高。

1 方法原理

与常规地面地震克希霍夫积分法叠前深度偏移类似,全平面域克希霍夫积分叠前偏移成像方法由偏移速度求取和克希霍夫积分偏移两部分组成,两者在实现过程中均涉及成像区域旅行时场计算,本文采用有限差分求解程函方程的方法计算节点旅行时。

1.1 有限差分程函方程初至旅行时计算

旅行时计算是积分法偏移成像的重要组成部分,其计算精度直接影响着成像效果,在高频近似下,平面波波前的传播符合程函方程式(1)^[9]:

(1)

{(\frac{\partial t}{\partial x})}^{2} + {(\frac{\partial t}{\partial y})}^{2} = s^{2} (x, z)

式中,t为初至时间;s(x,y)为平面模型的慢度场。

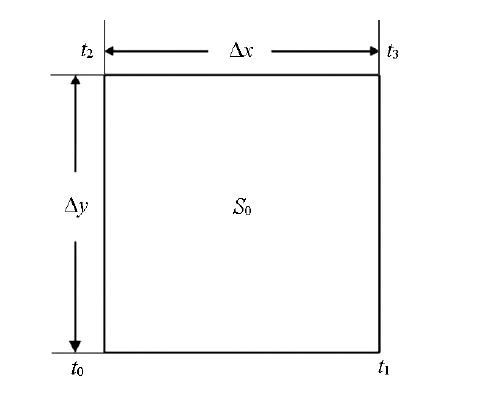
采用有限差分近似方法求解式(1),将速度模型离散成规则的矩形网格(图1所示),X、Y方向网格边长分别为Δx、Δy,将每个网格单元内的慢度视为常数,将方程中的两个时间微分算子用有限差分算子近似,如式(2)~(3)所示^[9,12]:

(2)

\frac{\partial t}{\partial x} = \frac{1}{2 Δ x} (t_{0} + t_{2} - t_{1} - t_{3})

(3)

\frac{\partial t}{\partial y} = \frac{1}{2 Δ y} (t_{0} + t_{1} - t_{2} - t_{3})

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 矩形网格剖分示意

Fig.1 Diagram of rectangular mesh partition

将式(2)、(3)代入式(1),经推导可以得到式(4)^[9]:

(4)

t_{3} = \frac{A (t_{0} + t_{1} - t_{2}) + B \sqrt[]{C s_{0}^{2} - (t_{1} - t_{2})^{2}}}{C}

式中,A=Δx²-Δz²,B=2ΔxΔz,C=Δx²+Δz²,已知矩形网格3个节点旅行时t₀、t₁、t₂可以利用式(4)得到旅行时t₃,计算中常常会出现根号下为负值而出现计算不稳定的情况,此时可将节点0、1、2视为散射源,按直射传播方式,分别计算节点3的初至时间,结合节点3的已有旅行时间,取5个值里面的最小值作为节点3的全局最小旅行时。

在旅行时场外推过程中,笔者采用Dijkstra算法逐点计算所有节点的全局最小旅行时,将所有计算节点分成3个子集,分别用P、Q、R表示,其中P为尚未计算旅行时的节点集合(节点旅行为无穷大),Q为已计算旅行时的节点集合(不确定是否为全局最小旅行时),R为已确定为全局最小旅行时节点的集合,采用如下方法对各节点的集合属性进行更新:

1)将所有节点置于P集合,且所有节点旅行时均置为无穷大,计算炮点所在网格4个节点的旅行时,将其置于Q集;

2)在Q集中选取旅行时最小的节点作为次级震源,并将其置于R集,计算该节点周围8个节点的旅行时,若待计算节点属于P集合,则将其置于Q集合,更新该节点旅行时;若节点属于Q集合,则将计算结果与先前结果比较,取小值作为该节点旅行时;若节点属于R集,则不改变原值;

3)重复步骤2)直至所有节点均属于R集为止,即可求得成像区域内所有节点的全局最小旅行时。

1.2 初至波层析成像反演速度场

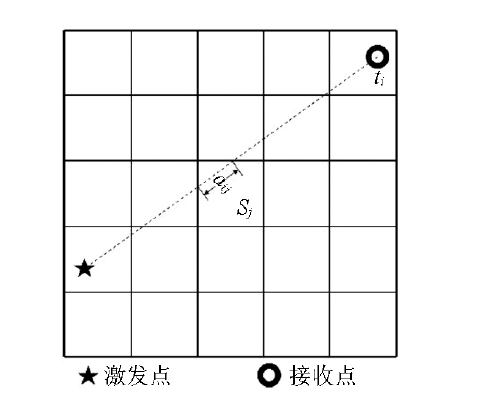
偏移速度场的计算精度直接影响着偏移成像效果,是克希霍夫积分法偏移成像的关键,对于非地面地震观测系统,采用地面地震观测系统的偏移速度分析方法获取偏移速度比较困难,通常采用初至波层析反演方法获得偏移速度,其中直射线层析成像方法应用比较普遍,如文献^[2-3]中的井下槽波绕射偏移成像,当反演区域速度差异较小时,可近似认为射线在介质中沿直射传播,如图2所示,炮检点间的射线路径为直线,a_i_,_j为第i条射线在第j个网格中的射线长度,S_j为第j个网格的慢度,t_i为第i条射线的初至时,利用直射线层析反演方法可以获得较可靠的成像速度,当成像区域速度变化较大时,由于实际射线路径常绕过低速区,并向高速区集中,射线路径发生较大弯曲,不满足直射线假设条件,常导致高速异常体偏大,低速异常体偏小^[13]。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 离散网格中直射线层析反演示意

Fig.2 Sketch of straight-ray tomography inversion in regular grids

为了克服直射线层析的这一缺陷,将成像区域进行网格剖分后,采用有限差分法求得各成像网格节点的全局最小旅行时,应用最速下降法反向求取炮检点间的射线路径^[11],在网格单元内认为射线路径为直线段,这样整体而言,炮检点之间的射线路径则是由一系列的直线段首尾依次连接形成的弯曲射线(图3),不妨设二维平面被剖分成N个网格,每个网格的慢度为s_j,获得了M条射线,假设第i条射线在第j个网格的射线长度为a_i_,_j,该射线的初至波旅行时为t_i,则可以得到该射线的旅行时方程如式(5)所示:

(5)

\sum_{j = 1} a_{i, j} S_{j} = t_{i}

图3

新窗口打开| 下载原图ZIP| 生成PPT

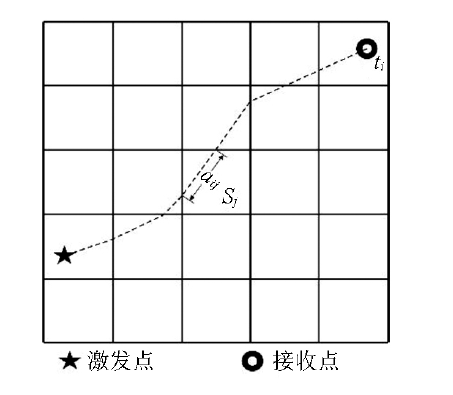
图3 离散网格中弯曲射线层析反演示意

Fig.3 Sketch of curve-ray tomography inversion in regular grids

式中,a_i_,_j为第i条射线在第j个网格中的射线长度,S_j为第j个网格的慢度,t_i为第i条射线的初至时,将所有射线方程联立可以得到线性方程组(6):

(6)

A \cdot S = T

其中,A=(a_i_,_j)_M_,_N为射线路径矩阵,S=(s_j)_N为慢度,列向量T=(t_i)_M为初至时间列向量,式中A通常为一大型稀疏病态矩阵,可采用ART、SVD、SIRT、LSQR、LSCG等算法对其进行求解,本文采用LSCG算法对慢度场进行更新,该算法是共轭梯度法的一种改进算法,对于大型线性方程组Ax=b,可将其转化为二次函数的极小点问题如式(7)所示^[14]:

(7)

f (x) = \frac{1}{2} x^{T} A^{T} Ax - (A^{T} {b)}^{T} x

。

函数f(x)的梯度g(x)为:

(8)

g (x) = \nabla f (x) = A^{T} Ax - A^{T} b

。

对于任意非零向量p和实数t,有:

(9)

f (x + tp) - f (x) \approx t g^{T} (x) p + \frac{1}{2} t^{2} p^{T} A^{T} Ap

于是有:

(10)

\frac{d f (u + tp)}{d t} |_{t = 0} = g^{T} (u) p = 0

。

考虑到p的随机性,必须有g(u)=0成立,因而u为方程组的解,对于共轭向量序列{p⁽^k⁾},假定x⁽⁰⁾是任一给定的初始向量,对于k=0,1,2,3,…,以x⁽^k⁾作为起点,沿方向向量p⁽^k⁾求函数f(x)在直线x=x⁽^k⁾+tp⁽^k⁾上的极小点,可以得到:

(11)

x^{(k + 1)} = x^{(k)} + α_{k} p^{(k)}

(12)

s^{(k)} = A^{T} (b - A x^{(k)})

(13)

α_{k} = \frac{s^{(k) T} p^{(k)}}{p^{(k) T} A^{T} A p^{(k)}}

以上3式中p⁽^k⁾表示搜索方向,如果取p⁽⁰⁾=s⁽⁰⁾,则有:

(14)

p^{(k + 1)} = s^{(k + 1)} + β_{k} p^{(k)}

(15)

β_{k} = \frac{s^{(k + 1) T} A^{T} A p^{(k)}}{p^{(k) T} A^{T} A p^{(k)}}

。

式(11)~(15)构成了LSCG算法的迭代格式,在迭代之前常给定初始解x⁽⁰⁾=0。从该迭代格式可知LSCG算法主要由大量Ax、A^Tx及矢量内积运算构成,为了提高计算速度降低内存消耗,在程序设计中采用三元组存储方式存储距离阵A^[15]。为了压制迭代过程中出现的反演噪声及野值,提高反演剖面的信噪比,采用均值滤波器对迭代的中间结果进行了平滑处理^[16]。

1.3 克希霍夫积分偏移

应用有限差分法分别计算以炮点和检波点作为激发点时各成像网格点的旅行时场后,可基于Kirchhof积分公式通过边界积分法实现地震数据成像,对于二维全平面域偏移成像问题,其离散形式如式(16)所示^[17]:

(16)

P_{out} = \frac{Δ x}{4 π} \sum_{A} \frac{\cos θ}{ν \sqrt[]{r}} \frac{\partial}{\partial t} P_{in}

值得注意的是:由于在偏移过程中对数据已做扩散补偿,因此在预处理时不应对数据再做扩散补偿处理。

2 数值模拟

2.1 模型建立

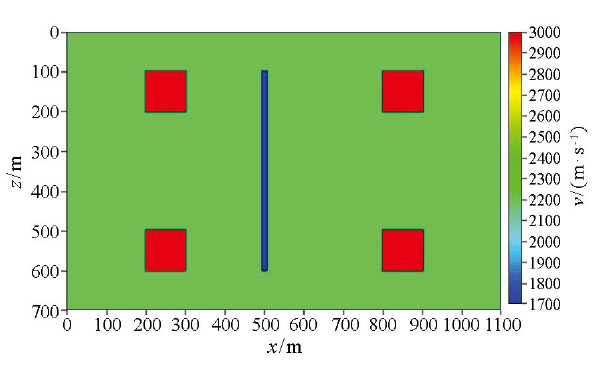
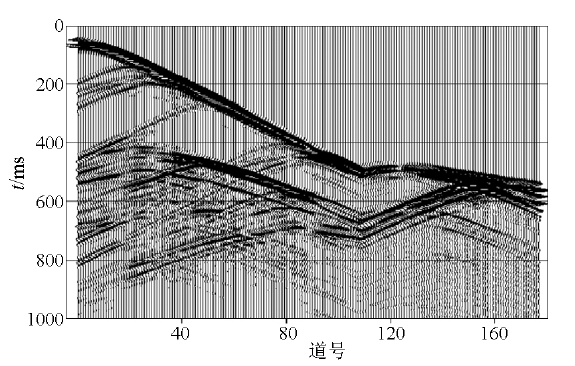
建立二维速度模型如图4所示,该模型横向长1 100 m,深700 m,背景速度2 200 m·s^-1,在模型上设置5个速度异常体,其中4个正方形速度异常体边长均为100 m,速度为3 000 m·s^-1,模型中间长条状异常体长500 m、宽10 m、速度1 700 m·s^-1。在模型左侧及顶部每隔20 m激发一单炮,地震子波为主频60 Hz的Ricker子波,共激发了92张模拟记录,并于模型顶部及右侧每隔10 m安置检波器接收地震信号,记录长度1 500 ms,采样间隔0.5 ms;图5为激发点位于(0 m,120 m)处的模拟单炮记录。由该单炮记录可以看出,对于图4的简单模型,地震波场特征比较复杂,单炮记录上发育有直达波、反射波、绕射波等。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 模型及观测系统

Fig.4 Model and observation system

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 模拟单炮记录

Fig.5 Simulate single shot record

2.2 层析反演速度结构

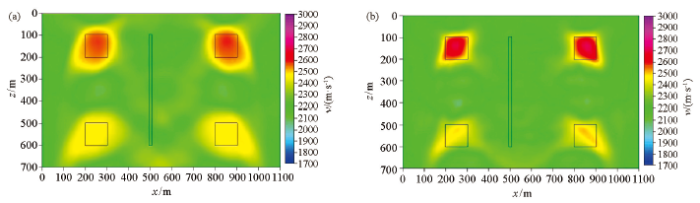
分别采用直射线和弯曲射线层析成像方法反演得到了成像区域的速度场,反演网格大小5 m×5 m,采用最小二乘共轭梯度(LSCG)反演算法共进行了10次迭代处理。采用二维平滑滤波器对迭代的中间结果进行平滑处理,以消除反演过程中的噪声及野值,提高反演剖面的信噪比。图6是两种层析方法获得的反演速度场(两张剖面速度色标一致),图中黑线为模型中速度异常体的边界,从该图可看到:两种层析成像方法获得图像的背景速度大约为2 200m·s^-1,与模型的背景速度一致,两种方法4个高速异常体在成像速度平面上均有显示;直射线层析剖面上高速异常体速度大约为2 600 m·s^-1,较模型速度低了约400 m·s^-1,异常体的边界比较模糊,且较真实尺寸偏大,形态畸变严重,模型中间的长条形低速异常体在反演剖面上并无明显异常;在弯曲射线层析成像剖面上,模型顶部两高速异常体的显示较直射线层析方法的分辨率高,边界形态刻画清晰,异常体速度大致为2 800 m·s^-1,精度较直射线方法有所提高,异常体大小与其实际尺寸较接近,模型底部两速度异常体由于观测方位的限制,畸变较严重,但仍较直射线成像方法更加收敛,模型中间的条形低速异常体成像也有所改善,异常体速度大约为1 900 m·s^-1,较真实速度略高。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 直射线(a)与弯曲射线(b)层析反演速度结构

Fig.6 Velocity structure by straight(a) and curve ray(b) tomography inversion

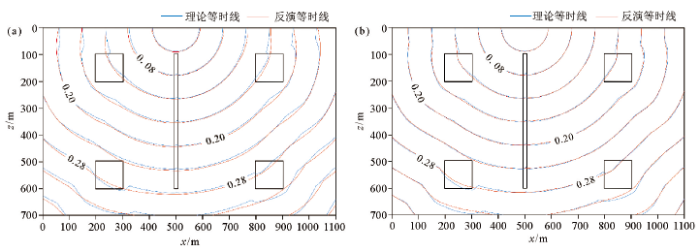
图7为炮点位于(500 m,0 m)处直射线层析和弯曲射线层析速度模型初至波时间等值线图,由该图可见弯曲射线层成结果的等时线与理论等时线的吻合程度明显优于直射线法,由于模型底部没有炮点和接收点,观测方位受限,两种反演方法获得的速度均不够准确,初至时间的误差较大。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 直射线(a)与弯曲射线(b)层析等时线图对比

Fig.7 Comparison of isochron maps of straight (a) and curve (b) ray tomography

2.3 克希霍夫偏移成像效果对比

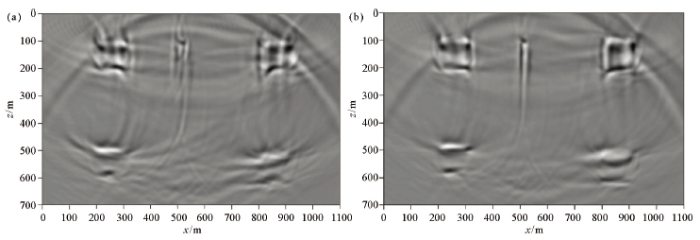
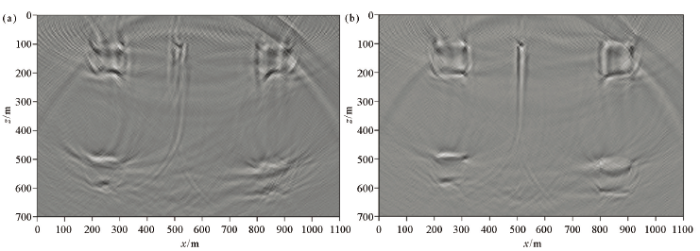
分别以基于直射线和弯曲射线反演的速度作为偏移速度,对模拟单炮数据进行时间偏移成像,成像网格为5 m×5 m。图8是两种不同偏移速度获得的原始成像剖面,可以看到:两种方法的原始偏移剖面上均存在较强的低频背景干扰,剖面信噪比和分辨率较低,笔者借鉴逆时偏移的低频噪声压制技术,应用Laplace差分滤波器对原始成像剖面进行了滤波处理,结果如图9所示,滤波后图像的信噪比和分辨率得到一定增强,速度异常体的边界更加清楚。对比图9中的两张剖面可以看出:两个偏移结果对所有速度异常体均有反映,基于直射线反演速度的成像剖面上4个高速异常体的形态发生了严重畸变,模型中间的长条形低速异常体反射波聚焦较差;以弯曲线CT反演的速度为偏移速度的成像剖面上,4个高速异常体的形状和大小均与原模型比较吻合,模型中间的长条型低速异常体上半部分成像清晰,下半部由于观测系统的原因,未能接收到有效反射波而不能成像。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 原始偏移成像剖面

a—直射线层析;b—弯曲射线层析

Fig.8 Original migration imaging profile

a—imaging profile of straight ray result;b—imaging profile of curve ray result

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Laplace滤波后的成像剖面

a—直射线层析;b—弯曲射线层析

Fig.9 Imaging profile after Laplace filtering

a—imaging profile of straight ray result;b—imaging profile of curve ray result

3 结论

本文以层析反演速度作为偏移速度,应用克希霍夫积分偏移方法对复杂二维模型进行了全平面偏移成像,通过对层析反演结果及偏移成像剖面的对比分析得到如下认识:

1) 对于复杂速度结构,直射线层析反演方法获得的速度异常的形态大小会发生严重畸变,且对小构造刻画不清,而弯曲射线层析算法可以较准确地反映速度异常体的形态和位置,对小构造的刻画较直射线清晰。

2) 克希霍夫积分法偏移技术是一种观测系统适应性强的偏移成像方法,以弯线射线层析反演速度作为偏移速度,采用克希霍夫叠前偏移方法可以获得较准确的偏移成像剖面。

3) 应用Laplace差分滤波器可以对原始偏移剖面上的低频噪声进行有效压制,提高成像剖面的信噪比和清晰度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

宋勇

Kirchhoff积分转换波叠前深度偏移方法研究

[D]. 西安:长安大学, 2015:4-5.