断溶体油藏油源深度对井温分布影响的数值模拟

doi:10.11720/wtyht.2020.1116

断溶体油藏油源深度对井温分布影响的数值模拟

胡文革^,¹, 邹宁¹, 李丹丹¹, 黄知娟¹, 雷健^,², 郭宇航², 潘保芝²

1.中石化西北油田分公司,新疆乌鲁木齐 830012

2.吉林大学地球探测科学与技术学院,吉林长春 130026

The numerical simulation for the influence of reservoir depth on well temperature in karstic-fault reservoir

HU Wen-Ge^,¹, ZOU Ning¹, LI Dan-Dan¹, WANG Zhi-Juan¹, LEI Jian^,², GUO Yu-Hang², PAN Bao-Zhi²

1. Sinopec Northwest Oilfield Company,Urumqi 830012,China

2. College of GeoExploration Sicence and Technology,Jilin University,Changchun 130026,China

通讯作者: 雷健(1992-),男,吉林大学在读博士研究生,研究方向为地球物理测井。Email:leijian18@mails.jlu.edu.cn

责任编辑: 叶佩

收稿日期: 2019-03-12 修回日期: 2020-05-20 网络出版日期: 2020-08-20

基金资助:

国家重大专项“塔里木盆地碳酸盐岩油气田提高采收率关键技术示范工程”. 2016ZX05053
中石化科研项目“顺北一区采输关键技术研究与应用——顺北一区完井技术研究与应用”. P18022-01

Received: 2019-03-12 Revised: 2020-05-20 Online: 2020-08-20

作者简介 About authors

胡文革(1966-),男,博士,教授级高级工程,从事油气田开发研究与管理工作。Email:huwg.xbsj@sinopec.com

摘要

塔河油田断溶体油藏蕴藏着丰富的石油资源,以大型溶洞和裂缝为主要储集空间和流动通道。在对断溶体油藏钻井时常发生泥浆漏失和井眼垮塌,难以进行常规测井测量,因而无法进行储层评价,甚至无法确定油层位置(即油源深度)。温度测井不受井眼条件的影响,可以测量关井时的静温和生产时的流温曲线,人们试图通过流静温度差异来推测油源的深度。本文依据断溶体油藏的形态特征和尺寸参数,构建多种井筒、地层与缝洞的物理模型,建立受流体流动影响的温度场,通过数值方法耦合温度场和流动场,模拟不同断溶体油藏石油生产时,井筒温度分布的变化。进而通过流温和静温的关系推测断溶体油藏油源位置,为断溶体油藏进一步的开发提供技术支持。

关键词： 断溶体油藏 ; 数值模拟 ; 井温曲线 ; 油源位置

Abstract

The carbonate karstic-fault oil-bearing reservoir is rich in oil resources storage,and large karst caves and fractures are the main reservoir space and flow channels.There are mud leakage and hole collapse in the drilling process,so it is difficult to carry out conventional logging measurement,and reservoir evaluation or even reservoir depth (i.e. oil source location) can not be determined.Temperature curve is often used in production logging,and it is not affected by borehole condition and it can reflect the depth of the reservoir.Based on the morphological characteristics and size of karstic-fault reservoir,the authors constructed the geometric models of wellbore,formation,fracture and cave,and simulated the variation of wellbore temperature in the production of karstic-fault reservoir by numerical simulation method.The simulation results were analyzed,and then the oil source depth of karstic-fault reservoir was estimated by well temperature curve,which provides technical support for further development of karstic-fault reservoir.

Keywords： karstic-fault reservoir ; numerical simulation ; well temperature curve ; reservoir depth

PDF (4515KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡文革, 邹宁, 李丹丹, 黄知娟, 雷健, 郭宇航, 潘保芝. 断溶体油藏油源深度对井温分布影响的数值模拟. 物探与化探[J], 2020, 44(4): 748-755 doi:10.11720/wtyht.2020.1116

HU Wen-Ge, ZOU Ning, LI Dan-Dan, WANG Zhi-Juan, LEI Jian, GUO Yu-Hang, PAN Bao-Zhi. The numerical simulation for the influence of reservoir depth on well temperature in karstic-fault reservoir. Geophysical and Geochemical Exploration[J], 2020, 44(4): 748-755 doi:10.11720/wtyht.2020.1116

0 引言

塔河油田位于塔里木盆地塔北隆起阿克库勒凸起的南部斜坡区^[1],在该区域发现了断溶体油藏^[2]。断溶体油藏的储集空间是中—下奥陶统碳酸盐岩层中沿断裂发育的大型洞穴、裂缝及沿缝溶蚀孔洞,物性圈闭是外围致密碳酸盐岩构成的侧向封挡^[3]。断溶体油藏的石油富集差异化明显,不同油藏开发效果差异较大,开发井“高产不稳产”,产油深度难以确定^[4]。

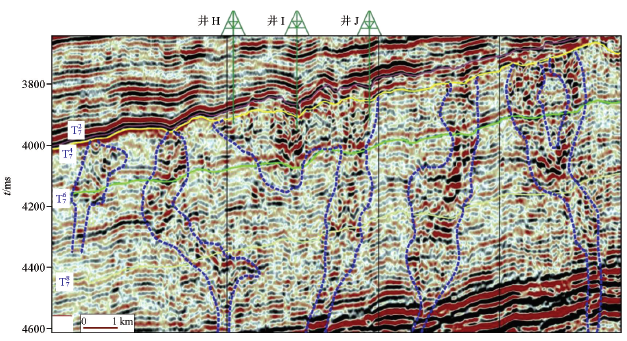
在断溶体油藏开发过程中,由于缝洞系统发育,钻井时常发生大量泥浆漏失与钻具放空的情形。在钻遇大型溶洞时往往封堵效果很差,这时无法继续钻进,而被迫完井。常规测井在漏失段和坍塌段都无法测量,导致生产时油源深度难以确定^[5]。

无论井眼条件如何,都可以测量井内温度剖面^[6]。井温测井是重要的生产测井方法之一,通过测量某一深度的井温或沿井剖面的温度变化,来确定生产油层的深度,了解井内流体的流动状态。油气生产过程中,井中温度不仅仅反映测量层段的温度信息,还受流体来源层段的温度影响^[7]。在关井后非生产时段,井筒中的温度逐渐与地层温度相同,这时的井温称为静温;产液过程对井筒和地层温度分布产生影响,在稳定生产时的井温,称为流温^[8]。

由于井筒和地层温度分布受到流体流动的影响,在断溶体油藏生产过程的温度场模拟中,需要同时考虑流动和能量传递,将温度场和流动场耦合计算。井中流体和周围地层通过传导、对流和辐射进行热交换,其中辐射作用很小可以忽略^[9]。作为断溶体油藏主要的储集空间和生产通道,大型溶洞、裂缝以及井筒中的流体流动不遵循达西定律,而是具有管流特征,满足 N-S方程,因此流体动力学是研究断溶体油藏流动的基础^[10-13]。

计算流体力学(CFD)是研究流体流动和能量传递规律的一种实用方法,利用离散方程描述连续的流动场和温度场,通过数值方法求解整个计算区域的流体性质^[14]。相应的CFD商业化软件可以实现模拟过程的可视化和参数精准检测,其中COMSOL软件具有强大的流体流动分析能力和多场耦合计算能力。

断溶体油藏是一种新型的石油富集圈闭,对该类油藏的温度分布规律尤其是生产时流温的评价方法还是空白。利用COMSOL软件,模拟断溶体油藏的石油生产过程中温度场的变化,进行流体流动场和温度场的耦合,分析不同井筒和溶洞关系时井中流温、静温曲线特征。为利用井中静温和流温差异研究储层与井筒的相对位置提供依据,为断溶体油藏的开发提供帮助。

1 数学物理模型及模拟方法

本文模拟的断溶体油藏生产过程为:①初始状态时,石油储存在溶洞中,温度分布就是地层原始温度;②钻井开发时,石油以一定的速度从溶洞进入井筒,井筒和周围地层的温度场发生改变,井中温度为瞬态温度;③稳定生产一段时间,井中温度分布达到稳态,不再变化,测得的井中温度为流温曲线;④关井一段时间后,井中温度逐渐恢复到与地层原始温度一致,流体静止,此时为静温。在热平衡建立的过程中,热量在井筒与地层中的传递存在5个典型阶段,分别为:原始温度分布被破坏、热量在井筒内做稳定径向导热、热量从井筒向地层传递、热量在地层内做径向导热以及达到热平衡^[15]。本文模拟采取稳态方法,不考虑生产时间和关井时间的影响,直接得到流温、静温曲线。

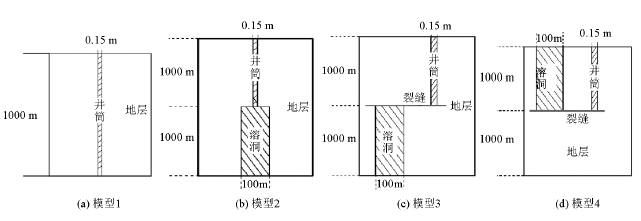
1.1 物理模型

塔河油田的断溶体油藏规模与断裂的发育密切相关^[16]。图1是断溶体油藏在地震图上的形态,可以看出沿着断裂的走向分布的众多溶洞,这些溶洞具有不同的形态。图中标出了3口井的位置,这3口井均与溶洞直接接触^[17]。唐海^[18]通过分析钻遇溶洞和地震等资料,总结得到了5 种典型的断溶体油藏形态,每种形态由不同数量和大小的溶洞构成。这些溶洞水平方向较窄,垂向延伸很深,在几何上接近于圆柱,由此本文模拟时采取圆柱形的溶洞形态。

考虑到生产井与油藏的相对位置存在的多种情况,文中确定了4种模型:①只有井筒(图2a);②井筒与溶洞直接相连(图2b);③井筒与溶洞通过裂缝相连,溶洞在下方(图2c);④井筒与溶洞通过裂缝相连,溶洞在井底上方(图2d)。根据研究区地震剖面等资料确定了模型的几何参数(图2),溶洞高为1 000 m,直径为100 m,钻孔直径为0.15 m,裂缝宽度为0.05 m。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 沿断层的地震图像(图中蓝色虚线区域为溶洞^[17])

Fig.1 Seismic image along the fault(The blue dotted line area in the figure is karst cave^[17])

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 物理模型示意

Fig.2 Schematic diagram of physical model

1.2 计算方法

利用COMSOL软件的流体传热模块进行稳态模拟。假设井筒、裂缝和溶洞中的流动为层流,地层为固体无流体流动,地温梯度恒定,不考虑热辐射。

通过数值计算和图像显示,对包含有流体流动和热传导等相关物理系统进行分析。文中基于CFD采用的基本算法是:用有限个离散点上的温度和速度的集合表示速度场和温度场,通过守恒方程组建立这些离散点上两种场变量之间的代数关系,然后求解代数方程组获得各个离散点上的温度和速度的近似值。

1.2.1 控制方程

在断溶体油藏生产过程的数值模拟中,流体的流动和传热受质量守恒、动量守恒和能量守恒方程控制。

1)流体流动方程

动量守恒

(1)

ρ (u \cdot \nabla) u = \nabla \cdot [- p + μ (\nabla u + {(\nabla u)}^{τ})] + F

质量守恒

(2)

ρ \nabla \cdot (u) = 0

。

2)传热方程

能量守恒

(3)

ρ C_{ρ} u \cdot \nabla T + \nabla q = Q

(4)

q = - k \nabla T

式中:ρ为流体密度,kg·cm^-3;u为流动速度,m·s^-1;μ流体粘度,Pa·s;p压力,Pa; C_ρ为恒压热容,J·(kg·℃)^-1;q热通量,W·m^-2;k为导热系数,W·(m·℃)^-1;T为温度,℃;F表示体积力,Q表示热源。文中不考虑重力等的影响,F=0;没有内部热源,Q=0。

1.2.2 边界条件

地层的外边界保持原始地温分布,T_Ω=T₀+g_T·h;

流动入口在溶洞底部,T_in=T₀+g_T·h, $u_{in} = ν;$

流动出口在井筒顶部p_out=0;

式中:T_Ω为地层边界温度,℃;T₀地面温度,℃;g_T为地温梯度,℃·m^-1;h为地层深度,m;T_in为入口处流体温度,℃;u_in为入口处流体速度,kg·s^-1;ν为流体流入溶洞速度,kg·s^-1;p_out为出口压力,Pa。相关的模拟参数见表1。图3为原始地温分布图,代表了静温的分布。

表1 模拟参数

Table 1 Simulation parameters

名称	符号	单位	值
石油密度	ρ	kg·m^-1	793.6
石油恒压热容	C_ρ	J·(kg·℃)^-1	2200
石油粘度	μ	Pa·s	0.002
石油导热系数	k	W·(m·℃)^-1	1
地层密度	ρ_f	kg·m^-1	2715
地层恒压热容	C_f	J·(kg·℃)^-1	700
地层导热系数	k_f	W·(m·℃)^-1	3.1
地温梯度	g_T	℃·m^-1	0.01818
地面温度	T₀	℃	23
石油流入速度	ν	kg·s^-1	1.39

新窗口打开| 下载CSV

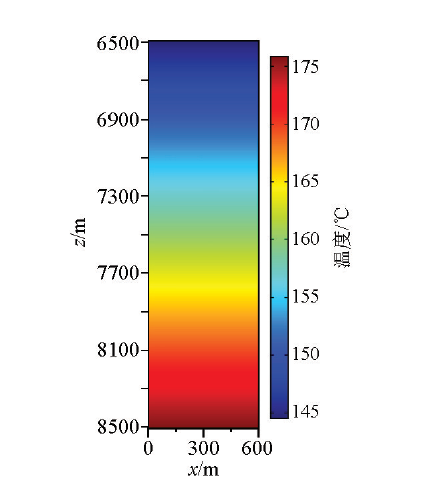
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地层的初始状态

Fig.3 Initial state of formation

1.3 模拟方法

1.3.1 网格剖分

在数值模拟中,物理模型的网格剖分精度对于计算结果有重要影响,COMSOL软件自带的网格剖分模块具有强大的功能,可以适应各种复杂模型。网格的剖分越细,模拟结果越精确,但是会增加网格数量,导致计算机内存需求和运算时间的增加^[19]。由于井筒直径、溶洞直径与地层直径的几何尺寸相差较大,本文采取分区域的网格剖分方法,即井筒、溶洞、裂缝和地层等不同区域的网格大小不同。将井筒、裂缝和溶洞部分的网格进行更密集的剖分,而地层部分采取较粗的剖分,通过在不同区域的连接处设置边界层实现地层与井筒等的耦合,图4为其中模型4的网格剖分。

图4

新窗口打开| 下载原图ZIP| 生成PPT

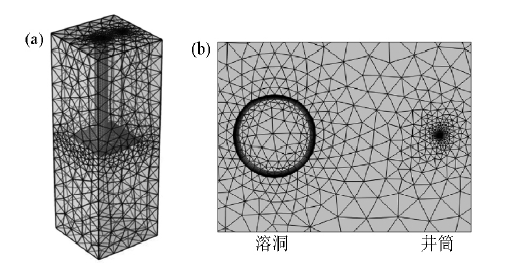
图4 模型4的网格剖分

a—整体剖分网格;b—溶洞和井筒的局部网格

Fig.4 Grid generation of model 4

a—global;b—karst cave and wellbore

1.3.2 温度场求解方法

由于石油流动和温度场相互影响,在模拟中需要考虑温度场和流动场的耦合问题。本文采用了COMSOL自带的稳态分离式求解器,该求解器在解决稳态多物理场问题时有良好的效果^[20]。求解步骤如下:首先假设初始的压力分布求解方程(1)得到速度分量;再将速度分量代入方程(2),检验速度求解是否正确;如果正确,将速度分量代入方程(3)和(4)求解温度场;如果不正确,使用压力修正,重新计算速度,直到得到满足精度要求的解(具体的计算过程参见文献[21])。

2 模拟结果分析

图5是只有井筒时(模型1)的温度分布和井温曲线。模型参数如下:井筒直径0.15 m,地层直径600 m,井筒长度1 000 m,井底位置在7 000 m。石油自井底流入井筒,流入时石油的温度与地层温度一致,此时井底流温和静温均为159.35℃。石油在井筒垂向热量对流传递效率远大于径向与地层的热传递。这样就导致生产时,井筒内的温度大于地层温度,高温石油将靠近井筒的地层加热,地层温度亦升高;稳定生产一段时间,地层温度和井筒内石油温度达到平衡,此时的温度分布如图5a和图5b,井筒内的流温曲线如图5c所示。可见流温与静温曲线在井底是一致的,向上流温逐渐大于静温。

图5

新窗口打开| 下载原图ZIP| 生成PPT

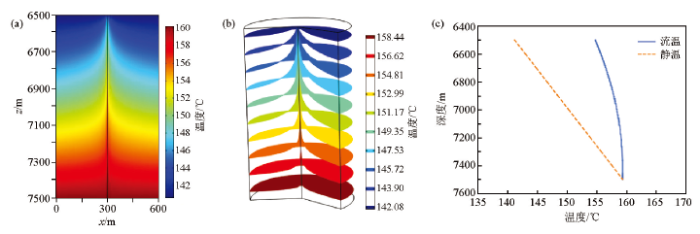
图5 只有井筒时(模型1)的温度分布和井温曲线

a—温度分布切面;b—温度三维分布;c—井温曲线

Fig.5 The temperature distribution and well temperature curve of the wellbore(model 1)

a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

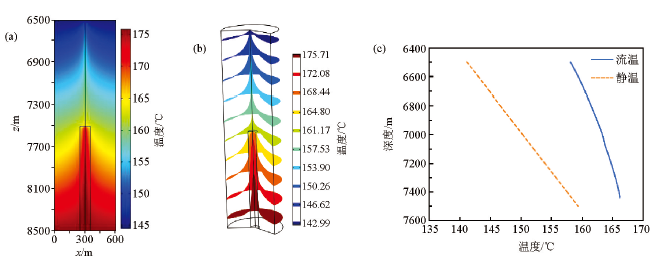
图6是溶洞在井筒下方时(模型2)的温度分布和井温曲线。模型参数为:井筒直径0.15 m,地层直径600 m,地层纵向厚度为2 000 m井筒长度1 000 m,溶洞直径100 m,长度1 000 m,井底位置在7 000 m,井底静温为159.35℃。石油在溶洞中流动时,由于与地层的接触面较小,且地层和石油的温差较小,溶洞中的石油冷却较慢,最终以较高的温度进入井筒,井底流温为 166.23℃。对比只有井筒时(模型1)的情况,存在溶洞时井底出现了较大的温度差异,且流温大于静温。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 溶洞在井底下方(模型2)的温度分布和井温曲线

a—温度分布切面;b—温度三维分布;c—井温曲线

Fig.6 The temperature distribution and well temperature curve when the cave is below the well-bottom (model 2)

a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

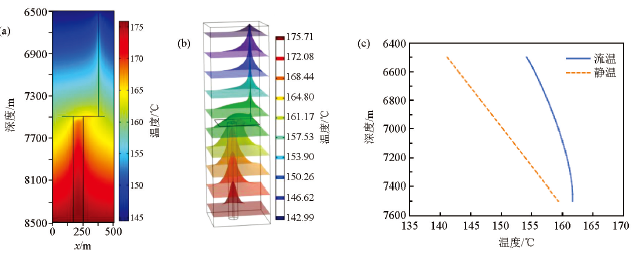
图7是溶洞在井底下方,通过裂缝与井筒相连时(模型3)的温度分布和井温曲线。模型参数为:井筒直径0.15 m,地层水平方向长宽均为500 m,地层纵向厚度为2 000 m,井筒长度1 000 m,溶洞直径100 m,长度1 000 m,裂缝宽度为0.05 m,井底位置在7 500 m,井底静温为159.35℃。石油通过裂缝进入井底时的流温为161.74℃。对比只有井筒时(模型1)的情况,井底温度差异较小,流温略大于静温。对比井筒直接与井筒相连的情况(模型2),模型3井筒中的流静温差较小。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 溶洞在井底下方(模型3)的温度分布和井温曲线

a—温度分布切面;b—温度三维分布;c—井温曲线

Fig.7 The temperature distribution and well temperature curve when the cave is below the well-bottom (model 3)

a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

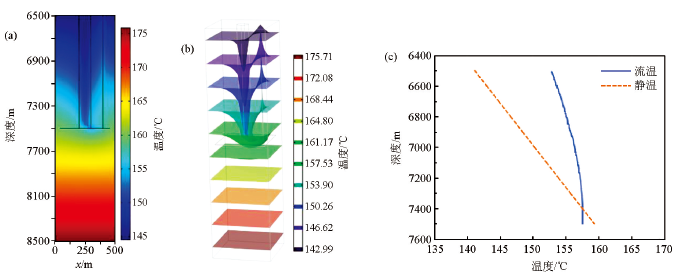
图8是溶洞在井底上方时(模型4)的温度分布和井温曲线。模型参数为:井筒直径0.15 m,地层水平方向长宽均为500 m,地层纵向厚度为1 600 m,井筒长度1 000 m,溶洞直径100 m,长度1 000 m,裂缝宽度为0.05 m井底位置在7 500 m,井底静温为159.35℃。由于溶洞在井底上方,温度较低的石油先向地层深部流动,逐渐被加热,但温度尚未上升到与地层温度一致即通过裂缝进入井筒。通过裂缝进入井筒时井底流温小于静温,井底流温为157.63℃。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 溶洞在井底上方(模型4)的温度分布和井温曲线

a—温度分布切面;b—温度三维分布;c—井温曲线

Fig.8 The temperature distribution and well temperature curve when the cave is at the above of the well-bottom (model 4)

a—section diagram of temperature distribution;b—three dimensional distribution of temperature;c—well temperature curve

3 实际井温分析

不同深度石油从溶洞进入井筒时的温度不同,测得的流温曲线也不同,图9是研究区A井和B井的实测和模拟流温、静温曲线,两口井在钻井和完井中均出现了泥浆漏失,目前均已稳定生产,产量约为90 t/d。使用表1的参数,结合已知的井底深度和产量数据,选择流温曲线形态相似的模型进行模拟。

图9

新窗口打开| 下载原图ZIP| 生成PPT

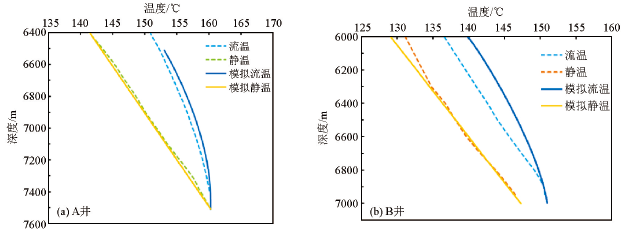
图9 实测与模拟井温曲线对比

Fig.9 Comparison of measured and simulated well temperature curves

结果如下:A井井底在7 400 m,温度160.114℃,此深度的静温为158.733℃,温差1.381℃,该井的流温曲线形态与模型1相似,模拟结果显示该井的油源深度在7 510 m。B井井底在6 950 m,此深度的实测流温为150.947℃,静温为146.56℃,温差4.387℃,该井的井底流静温差较大,形态与模型2的模拟结果相似,推断溶洞在井孔下方,依据油源深度为7 500 m时的模拟结果(图9b的蓝色实线),推测该井的油源深度为7 500 m。

4 结论

断溶体油藏作为一种新型的石油富集圈闭,急需有效的测井评价方法,以确定储层深度。文中通过对不同井筒和溶洞相对位置设置不同的断溶体模型,模拟了受石油流动影响的温度场,发现利用井中流温、静温曲线可以确定断溶体油藏储层位置。当产油层位于井底时,井底的流温、静温一致;当石油产自井底上方时,井底流温小于静温;当石油产自井底下方时,井底流温大于静温。通过实测的流温与静温曲线的形态,可以推断合适的溶洞—井模型,结合油井的生产数据通过数值模拟计算出油源位置。在之后的研究中需要进一步确定流温曲线与油源位置的定量关系,以便更快捷地确定油源深度和溶洞大小等信息。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

杨德彬

塔河油田断溶体油藏地震反射特征类型及规律

[J]. 石化技术, 2018,25(4):121-122.