0 引言
在实际情况中,静态效应是不可避免的,实际测量数据多少会受到静态效应的影响,当影响过大时则会影响到采集数据的准确性,给出错误信息。为了获取准确的地下结构信息,在进行数据处理前必须进行静态效应的判定和校正。
1 现有静位移校正方法简介
当前静位移校正的方法有:首枝重合法、曲线平移法、空间域滤波法、EMAP滤波法、小波分析法等,目前使用最多的是曲线平移法、空间滤波法和EMAP滤波法。
曲线平移法:在一个局部范围内,可以将深部地层看成沿水平方向连续分布的,在此假设条件下可以认为相邻测点的低频(深部)数据在没有地质异常的情况下沿测线方向具有连续性。因此,可以先根据已有的其他资料得出该区的视电阻率背景值,并将其他测点的实测数据资料与该背景值做比较,判断出受静态效应影响的测点,分析其影响程度,计算静态位移量,在此基础上,对受静态效应影响的测深曲线进行平移归位,达到静态校正之目的,减小或消除其影响。从操作的可行性或尽量综合已知地质物探信息的角度考虑,曲线平移法仍是目前进行静态位移校正的主要手段。但目前的平移法存在下列不足:①必须建立在对地质资料相当了解的基础上;②只能逐点进行,当测点较多时(一条剖面上可能会有几百个点),处理不但费时费力,而且效果因人而异;③对于三维的 MT 资料处理不仅要考虑到剖面上的连续性,同时还要考虑到平面上的连续性,用平移法校正难以实现[3]。
电磁阵列剖面法(EMAP):由美国地球物理专家 Bostick针对消除MT 法中静态干扰而提出的一种全新数据采集和处理方法,其实质是依靠密集数据,尽可能多地提取区内地电信息,采用低通滤波手段消除浅部电性横向不均匀性和局部地形起伏造成的静态影响,从而提高数据解释质量[6]。由于勘查成本的原因,目前我国主要应用 MT方法进行深部构造调查,测点分布疏散,点距在数千米以上,难以应用 EMAP 的处理方法。
以上各校正方法均具有一定的局限性,并不能通用于各种不同条件下的静位移校正。尤其是在测点与测点之间可参考性较低情况下,如何正确进行静态位移校正是取得可靠反演结果的关键。
2 首枝频点统计求平均法
连片静位移区测点静态偏移校正法的关键在于没有较近测点的参考下,如何正确地确定视电阻率曲线的首枝应该到达的正确位置。有 2 种方法可以确定一个测点视电阻率曲线首枝的正确位置:其一是通过岩石电性参数测量结果获得工区内各个地层的电阻率,依据测点所在位置的表层或浅层地层可得到首枝的正确位置;其二是在没有岩石测试资料的情况下, 通过分析判断出不受或少受静态偏移影响并且资料质量较好的测点, 通过统计各个出露地层上测点的视电阻率曲线首枝,获得各地层的电阻率。
本文基于岩性分析,初步总结出一套针对大点距的静态位移校正方法——首枝频点统计求平均法:把同一地区的所有测点投影到地质图上,按照地层和岩性的不同来统计测点,并把测点分类,取每个测点的前三个频点的视电阻率值,即高频部分的视电阻率值,分别算出每个测点的前三个频点的xy与yx的视电阻率平均值,根据算出的平均值得到每个出露地层区域测点视电阻率值的散点分布情况,剔除异常点之后,再计算出各出露地层区剩余测点的xy、yx视电阻率平均值,根据该平均值对出现静位移的测点进行校正,在不改变曲线形态的前提下,改变测点曲线首枝位置(曲线平移),使测点曲线的首枝达到正确位置。
3 应用实例
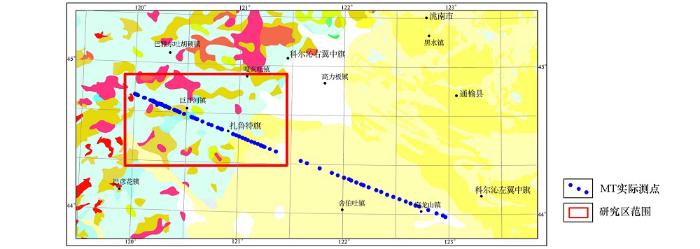
图1
3.1 静校正前的数据处理
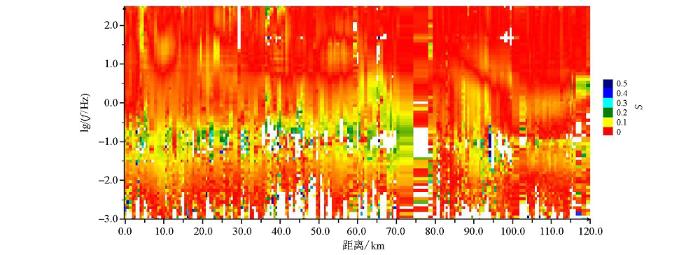
首先是静态位移识别问题。山区对大地电磁测深的影响一直是困扰大地电磁工作的一个难题。受地形影响,大地电磁测深工作野外布点相对困难,多数只能步在山沟或山沟两侧稍微平缓的地方,而沿山沟走向和垂直山沟走向的第四纪风化残积物存在一定的沉积差异,山体表现为高阻特征,对垂直山体方向的电场具有排斥作用,这就造成沿山体不同方向的电磁场分布不均匀,两条不同极化方向的视电阻率曲线出现差异,而且山体不规则时,影响更复杂[7,8]。确切地说,地形的起伏及地下介质的非均匀性,造成感应电流并非沿水平方向流动,在不均匀体周边产生电流的密集或稀疏现象,导致地表观测的电场分量增大或减小,最终反应在视电阻率曲线上呈现抬升或降低现象,对于二维剖面反演来讲,通常将其归结为静位移(或静态效应)。在大地电磁数据采集过程中发现,在大兴安岭东缘山区不少测点出现xy和yx视电阻率曲线高频分开的现象,局部区域现象明显。根据野外调研情况及图2中的海拔线可知,0~100 km范围内是大兴安岭山区,植被茂密,海拔较高,沟壑纵横,地形起伏较大。不管地形地貌还是测点曲线,表现出的畸变特征都与前人所遇情况类似,故而认为该区域测点曲线出现的畸变特征为静位移现象。
图2
沿测线往东,地形较平坦,基本为牧区或农区,东部的平原区上部被厚厚的第四系沉积层覆盖,xy和yx视电阻率曲线高频分开的现象不明显,可认为静位移现象较弱。
在进行静校正之前还需要对剖面数据进行维性分析,电性主轴分析,极化模式判别及选取等工作。
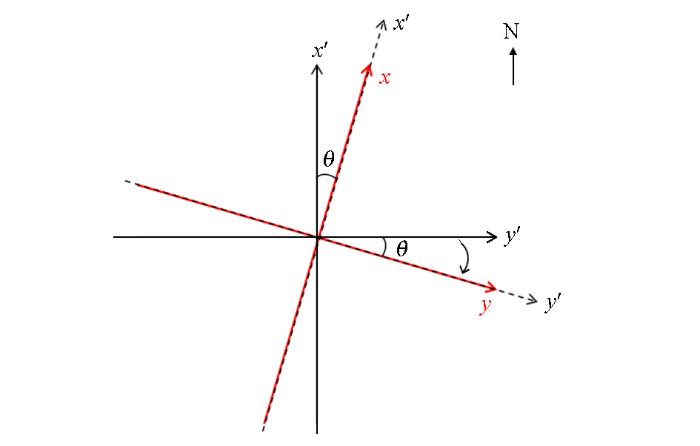
关于极化模式判别及选取问题,MT数据极化模式的判别一般和主轴分析同时进行,基于局部服从整体的考虑,利用多测点—多频点统计成像分析技术获得研究区主体构造主轴方向[10,11],通过旋转将观测坐标系旋转到构造主轴坐标系(图3),则Rxy、Pxy代表TE极化模式下的视电阻率和相位,Ryx、Pyx代表TE极化模式下的视电阻率和相位。对不同极化模式数据反演来说,TE极化模式特点是纵向分辨率高,分层好,对模型二维性要求高;TM极化模式特点是横向分辨率高,对模型二维性的要求低,受三维畸变影响小,对异常体识别好,在研究地球深部电性结构时,探测深度和分辨能力好,但受边界效应影响大。一般认为:反演优先选取TM模式,其次TE+TM模式,不单独使用TE模式。因此,本次实验中采用TM极化模式数据进行二维反演。
图3
图3
构造主轴坐标系x-y和观测坐标系x'-y'
Fig.3
Principal structural axis coordinate system x-y and observation coordinate system x'-y'
3.2 静校正
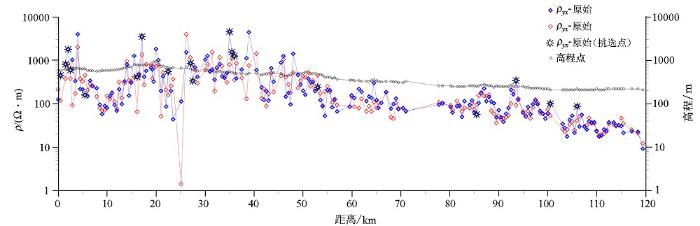
反演前还需要对视电阻率曲线进行静校正。一般认为静位移最直接的表现特征就是ρxy和ρyx首枝分离,从图4可看出,静位移现象严重的测点主要分布在0~40 km范围内。由于该条剖面测点相对较密,0~115 km的正常测点都是500 m左右的点距,点距比较小,浅地表相同岩性横向电性特征小范围内一般不会发生较大改变,同一测点两支视电阻率曲线的高频段在数据值上应趋于一致,如果有测点的视电阻率首枝突然出现明显的分离现象,则可认为该测点存在静位移影响。另外,针对小点距的测区,根据测点相近相似原理,在浅地表相同岩性区,邻近测点同一极化模式的视电阻率曲线形态应较接近,且高频段应趋于一致或缓慢变化,若出现孤立无规律的阶跃式变化,则应考虑静位移的影响。从该条剖面来看,部分区域连续多个测点首枝分离,且邻近测点出现无规律阶跃式的变化,我们认为其存在静位移现象,尤其是西部构造复杂的大兴安岭东缘地区,若不对这些测点进行静校正处理,将大大影响反演结果。为此,在连续出现静位移区,间隔5~10 km挑选出部分测点进行静位移校正尝试。
图4
图4
320 Hz频点的ρxy、ρyx沿剖面变化曲线
Fig.4
Variation of 320 Hz-ρxy and ρyx along the profile
选取的研究区剖面长120 km(见图1红色框内),共99个测点,点距500~1 000 m不等。地表出露第四系、侏罗系、二叠系等多套地层,出露地层为第四系的分布测点有47个,出露地层为侏罗系的分布测点有42个,出露地层为二叠系的分布测点有10个。根据出露地层和岩性的不同对其内分布的测点进行统计,继而得到不同地层不同岩性分布区内测点的视电阻率曲线。
根据野外测点数据采集情况,取每个测点的前三个频点(320 Hz、265 Hz、229 Hz)的视电阻率值,即为a、b、c三点,分别算出前三个频点的xy与yx的视电阻率平均值:
根据算出的平均值得到每个出露地层区域测点视电阻率值的散点分布,如图5所示。
图5
图5
测点曲线首枝电阻率统计值散点分布
Fig.5
Resistivity statistics of the first branch of the measured point curve
统计同一套出露地层中测点前三个频点(320 Hz、265 Hz、229 Hz)的xy与yx视电阻率平均值,剔除异常点之后,再计算出各出露地层区剩余测点的xy视电阻率平均值与yx视电阻率平均值。如图5,出露的全新统地层中,2号点和20号点的xy与yx的视电阻率平均值差值过大,视作异常点去除,利用剩余测点的xy、yx的视电阻率平均值分别进行计算:
根据该平均值对含有静位移的测点进行校正,即在不改变曲线形态的前提下,将测点曲线第二个频点的视电阻率值移至算出的平均值位置,进行整体的曲线平移,以此为标准把测点曲线校正至合理位置。
前文提到采用TM极化模式进行二维反演通常可以构建出准确的地下电性结构信息,因此,本次实验的大地电磁测深剖面只对TM极化模式的视电阻率曲线进行静校正处理和反演。
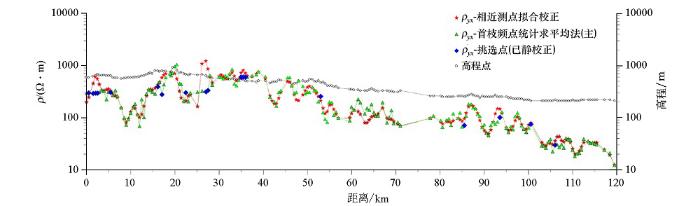
图6中绿色三角代表在连片静位移区域基于首枝频点统计求平均法进行校正之后的值,在静位移现象不明显区域基于测点相近相似原理进行静校正,红色五角形代表完全基于测点相近相似原理进行静校正,蓝色菱形为一些有代表性的点。
图6
图6
265 Hz频点ρyx相邻测点拟合校正与首枝频点统计求平均法校正对比
Fig.6
Comparison of 265 Hz-ρyx results with adjacent measurement point fitting correction method and first branch frequency point statistical averaging method
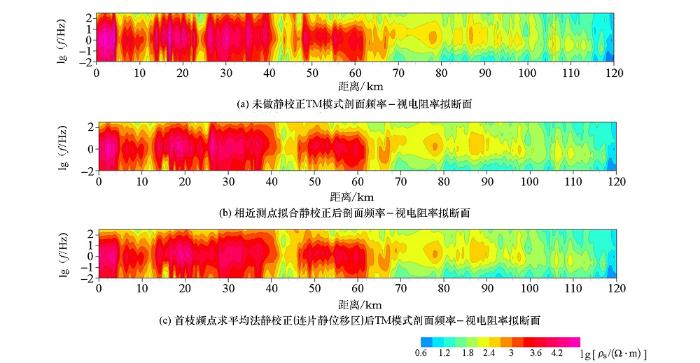
图7
图7
MT剖面TM极化模式频率—视电阻率拟断面对比
Fig.7
Frequency-apparent resistivity pseudo-cut face-to-face graphs of the MT section with TM polarization mode
3.3 校正前后的反演结果对比
对校正前和校正后数据开展二维反演。二维反演采用非线性共轭梯度法(NLCG),初始模型选择一维Occam反演迭代20次的结果,一维和二维反演均采用TM极化模式数据,二维反演选择一维Occam反演的结果作为初始模型,视电阻率和相位值的地板误差(floor error)为5%,正则化因子为5,反演最大迭代次数设置200,反演结果以最终收敛的结果为准。
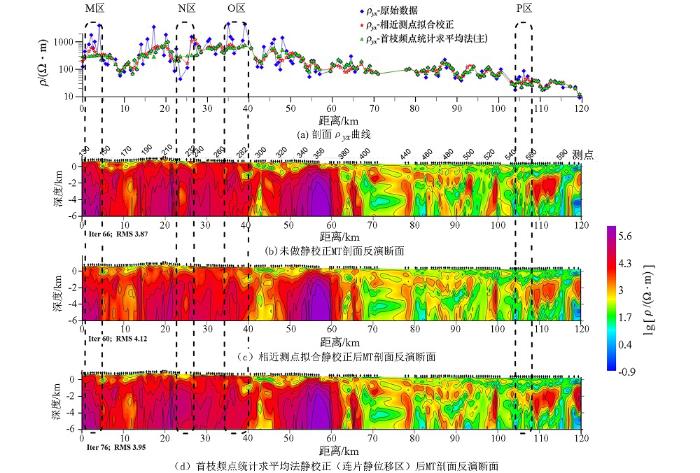
图8
总的来说,在连片静位移区MT剖面不做静校正直接反演,结果会存在一些明显的近直立假构造,所以必须要做静校正。利用测点相近相似原理进行拟合静校正后的反演结果和针对连片静位移测点区以首枝频点统计求平均法为基础进行静校正后的反演结果相比,近直立的假构造明显较少变弱,尤其是在测点与测点之间可参考性较低的情况下,首枝频点统计求平均法明显效果更突出,可以作为一种静位移校正的参考方法。
4 结语
本文基于岩性分析,初步总结出一套针对连片静位移区的静态位移校正方法——首枝频点统计求平均法。该方法在不改变曲线形态的前提下,改变测点曲线首枝位置(曲线平移),使测点曲线的首枝达到统计出的预置位置。在扎鲁特地区进行的实验结果表明,该方法具有一定的约束条件,获得的结果相对更真实些,对于静态效应的压制较好,效果更为突出。
在没有大量测井和物性约束条件下,首枝频点统计求平均法具有一定的合理性和参考性。未来如果有密集的采样物性和测井资料作为约束条件,相信对于超稀网度的三维大地电磁测深点的静校正工作也具有指导意义。
参考文献
关于大地电磁的静校正问题
[J].
Problem about static correction in magnetotellurics
[J].
大地电磁数据静位移影响及校正方法研究
[D].
The study of the impact on the magnetotelluric data from the static shift and the correction method
[D].
浅部不均匀体对目标体电阻率异常影响的研究
[J].
A study on effects of shallow inhomgeneous body on object resistivity anomaly
[J].
大地电磁测深静态效应空间域拓扑处理技术研究
[J].
Spatial domain topological processing technique for studying static effect in magnetotelluric sounding
[J].
Basic theory of the magneto-telluric method of geophysical prospecting
[J].
大地电磁静态效应校正方法对比研究
[D].
Contrastive analysis of different static shift correction methods in Megnetotelluric
[D].
大地电磁测深中的地形影响与校正
[J].
Terrain influence and correction in mt sounding
[J].
起伏地形大地电磁二维反演
[J].
An analysis of Google Earth elevation data accuracy and its application to seismic exploration
[J].
A magnetotelluric investigation of an electrical conductivity anomaly in the southwestern United States
[D].
大地电磁三维畸变特征及校正新技术的应用研究
[D].
The feature of three-dimensional distortin in MT and research of new correction methods
[D].
大地电磁资料精细处理和二维反演解释技术研究(四)——阻抗张量分解的多测点—多频点统计成像分析
[J].
Refined techniques for magnetotelluric data processing and two-dimensional inversion(IV):Statistical image method based on multi-site,multi-frequency tensor decomposition
[J].