航空重力测量数据的小波滤波处理

图1 小波包分解树(3层)

Fig.1 Wavelet decomposition tree at level 3

图2

图2 小波分解单元

Fig.2 Unit of wavelet decomposition

小波包分析不仅对信号的低频分量进行分解,也对高频分量进行分解,信号S={s(k)}的3层小波包分解树如图3所示,小波包分解单元如图4所示,j为小波包分解层次,n为第j层的小波包节点序号(n可能值:0,1,…,2^j-1),d_j_,_n为小波包节点(j,n)对应的小波包分解系数^[17]。

图3

图3 小波包分解树(3层)

Fig.3 Wavelet packet decomposition tree at level 3

图4

图4 小波包分解单元

Fig.4 Unit of wavelet packet decomposition

选用正交或双正交小波,则小波包系数分解与重构算法如下:

分解问题是:已知系数d_j_,_n,求系数d_j_+1,2_n和d_j_+1,2_n₊₁。分解公式为^[15,20-22]

(1)

\{\begin{array}{l} d_{j + 1,2 n} (k) = \sum_{l \in Z} h (l - 2 k) d_{j, n} (l) \\ d_{j + 1,2 n + 1} (k) = \sum_{l \in Z} g (l - 2 k) d_{j, n} (l) \end{array}

重构问题是:已知系数d_j_+1,2_n和d_j_+1,2_n₊₁,求系数d_j_,_n。重构公式为^[15,20-22]

(2)

\begin{array}{l} d_{j, n} (k) = \sum_{l \in Z} \overset{̅}{h} (k - 2 l) d_{j + 1,2 n} (l) + \\ \sum_{l \in Z} \overset{̅}{g} (k - 2 l) d_{j + 1,2 n + 1} (l), \end{array}

其中:h、g分别为低通和高通分解滤波器系数, $\overset{̅}{h}$ 、 $\overset{̅}{g}$ 分别为低通和高通重构滤波器系数。

1.2 小波包分解系数的频率顺序

对于信号分析来讲,重要的是将小波包系数按频率顺序排列,而不是按小波包节点的自然顺序排列。由于小波包分解时,每对高频系数进行一次分解,相应分解系数的频率排位顺序就会“翻转”一次,从而造成频率顺序与节点自然顺序不一致现象^[15,21]。按此规律,可推算出小波包分解系数频率顺序与对应小波包节点号的对应关系。以3层小波包分解为例,按前所述规律,可推算出小波包分解系数频率由小到大排位与节点序号的对应关系,具体分析结果见表1。由表1进一步分析可推算小波包分解系数频率由小到大对应节点号的顺序,如第3分解层的小波包分解系数频率由小到大对应节点号的顺序为(3,0),(3,1),(3,3),(3,2),(3,6),(3,7),(3,5),(3,4)^[15,21]。

表1 小波包系数频率排位与节点序号(3层)

Table 1 The “frequency” order of wavelet packet coefficients and natural nodes order at level 3

j(层次)	分类名
0	节点、频率排位(n)
1	自然节点顺序(n)				1
1	频率排位(n)				1
2	自然节点顺序(n)		1		2		3
2	频率排位(n)		1		3		2
3	自然节点顺序(n)	1	2	3	4	5	6	7
3	频率排位(n)	1	3	2	7	6	4	5

1.3 小波包系数的阈值处理

小波包系数阈值处理的关键是阈值估计和阈值施加方案。小波包分析中有4种常用的阈值估计方法和3种简单的阈值施加方案,具体如下:

4种阈值估计方法^{[11,13-15,17,21]}:① 自适应阈值(Rigrsure);② 固定形式阈值("sqtwolog");③ 启发式阈值(Heursure);④ 极小化极大阈值(Minimax)。

3种阈值施加方案^[19]:① 硬阈值处理(Hard Thresholding);② 软阈值处理(Soft Thresholding);③ 比例阈值处理(Percentage Thresholding)。

除上述方法和方案外,还有多种阈值估计方法和阈值施加方案。具体采用何种阈值估计方法和阈值施加方案取决于实际的应用,后续将结合航空重力测量数据处理做进一步探讨研究。

2 小波低通滤波器设计

基于小波包分析方法,按估算的小波包分解层次对应的信号频率范围、低通滤波器的截止频率和小波包系数频率节点的排列顺序,优化小波包树,设计小波低通滤波器。小波低通滤波器的设计需重点关注3个方面:小波的选取、小波包树的优化设计和小波包系数的阈值量化处理。

2.1 小波的选取

正交或双正交小波包分解可将信号按频率分解到无重叠的子带上,易于小波包快速算法的实现。因此,在小波包分析中,小波滤波器通常是选用正交或双正交小波来实现的。常用的正交、双正交小波有Discrete Meyer小波(dmey)、Daubenchies小波系(dbN)、Symlets小波系(symN)、Coiflet小波系(coifN)和Biorthogonal小波系(biorNr.Nd)等^[17]。

不同类型的小波系有不同的特性,其主要特性见表2^[17]。具有紧支撑集的小波(时域或空域),局部化能力强,易于算法实现;对称性使小波滤波器具有线性相位,避免了信号失真;消失矩的大小决定了用小波逼近光滑函数的收敛率;正则性是与光滑性相关联的,正则性越好,重构信号就越光滑,而光滑性决定了滤波频率分辨率的高低^[10,17,24]。

表2 常用正交或双正交小波系的主要特性。

Table 2 Wavelet families and main associated properties。

小波系	dmey	dbN	symN	coifN	biorNr.Nd
紧支撑性		●	●	●	●
正交性	●	●	●	●
双正交性					●
对称性	●				●
准对称性			●	●
消失矩		●	●	●	●
正则性		●	●	●	●
正交分析	●	●	●	●
双正交分析	●	●	●	●	●
精确重构	●	●	●	●	●

Daubechies原理表明除Haar小波以外不存在对称的紧支撑正交小波^[18],且紧支撑性与光滑性二者不可兼得^[10]。构造一个有正交性、紧支撑集、平滑性和对称性的小波是困难的^[10],应根据应用实际需求,在各项特性指标间做出取舍,选择适合的小波。

2.2 小波包树的优化设计

信号的多尺度小波包分解相当于带通滤波(分频),对于第j小波包分解层,每个节点分解系数的频带宽度为2^-^j Hz(采样频率1 Hz)^[17,20,24]。根据滤波器的截止频率和估算的分解层次对应的信号频率范围,选取分解层次N,并优化设计小波树。如周期为60 s的低通滤波器,相对应截止频率f_c近似为 0.016 7 Hz(注f_c≈2^-6+2^-10+2^-14≈0.016 7 Hz),取分解层次N=14,按小波包系数频率由小到大对应的小波包节点号顺序,优化设计小波包分解树,如图5所示。

图5

图5 小波低通滤波器的小波包分解树(滤波周期:60 s) 。

Fig.5 Wavelet packet decomposition tree of the low pass filter (filtering period: 60 s) 。

2.3 小波包系数阈值量化处理方案

采用正交或双正交小波滤波器对数据进行滤波处理,可将数据按频率划分为若干子带。按小波包系数频率大小,分别采用不同的阈值准则和处理方案,对小波包系数进行量化处理。现以60 s低通滤波器为例,加以具体说明。

按1.2小节所述方法分析可知:小波包低频系数频率由小到大对应的小波包节点号顺序为(6,0),(10,24),(14,408),高频系数频率由小到大对应的小波包节点号顺序为(14,409),(13,205),(12,103),(11,50),(9,13),(8,7),(7,2),(5,1),(4,1),(3,1),(2,1),(1,1)。按照小波包系数频率大小,分别采用不同的阈值方案进行处理。以异常信号为主的低频段,阈值要小;而以噪声为主的高频段,阈值要大。具体方案如下:

方案1:保留全部低频系数,高频系数全部都置“零”;

方案2:节点(6,0)低频系数进行平滑处理,节点(10,24)和(14,408)低频系数按估算比例压缩或

采用通用阈值估计进行量化处理,各层高频系数全部都置“零”;

方案3:在方案2基础上,节点(14,409)高频系数(过度频带)采用通用阈值估计进行量化处理,其余各节点高频系数全部都置“零”;

方案4:在方案3基础上,节点(13,205),(12,103),(11,50),(9,13)高频系数采用通用阈值估计进行量化处理,其余各节点高频系数全部都置“零”。

对于航空重力异常测量信号来讲,由于小波包分解低频系数同时包含信号和噪声两部分,且不同节点小波包系数的信噪比也不相同,故通用阈值处理方案有其局限性。在通用阈值处理方案基础上,本文提出的小波包系数阈值处理方案,针对不同节点的小波包低频系数采用平滑或按估算比例压缩的方法压制高频(相对)噪声,故能显著提高滤波精度。

3 滤波试验

图6为GT-1A系统3010测线原始未滤波航空自由空间重力异常测量数据,异常信号被幅度大致在±5 000 mGal的噪声信号所淹没,横轴Fid为测线基准点号,间距平均为30 m^{[2,7-9 ]}。选用正交或双正交小波,采用本文提出的阈值处理方案和设计的小波低通滤波器,对图6原始未滤波数据进行了低通滤波试验研究,并与GT-1A系统软件滤波结果进行对比分析。

图6

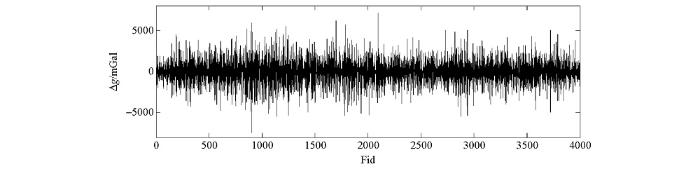
图6 GT-1A系统原始未滤波航空自由空间重力异常。

Fig.6 GT-1A raw unfiltered airborne gravity free air anomaly。

3.1 小波包树的优化设计

在航空重力测量中,低通滤波器的截止频率f_c一般在0.005~0.016 6 Hz之间,也就是滤波周期为200~60 s^[5]。试验中,小波低通滤波器的滤波周期选取具有代表性的60 s和100 s(对应的截止频率f_c分别为0.016 7 Hz 和0.01 Hz),优化设计的小波包树分别如图5和图7所示。

图7

图7 小波低通滤波器的小波包分解树(滤波周期:100 s) 。

Fig.7 Wavelet packet decomposition tree of the low pass filter (filtering period: 100 s) 。

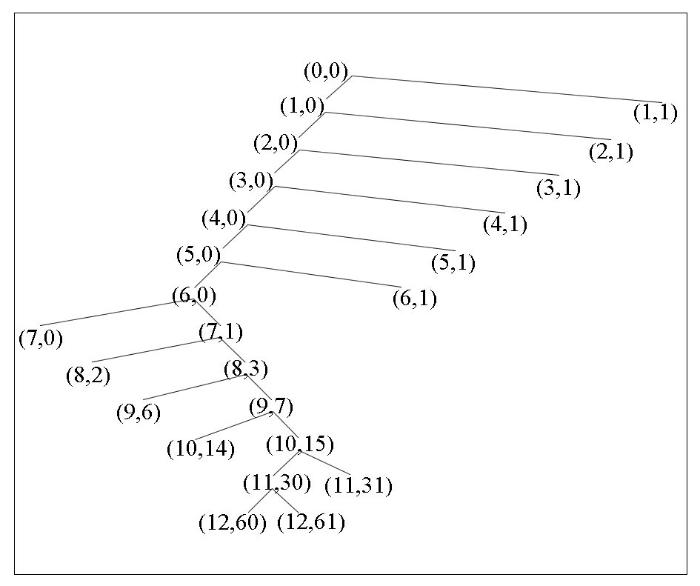
100 s与60 s小波低通滤波器的设计方法相同,其小波包低频系数频率由小到大对应的小波包节点号顺序为(7,0),(9,6),(12,60),高频系数频率由小到大对应的小波包节点号顺序为(12,61),(11,31),(10,14),(8,2),(6,1),(5,1),(4,1),(3,1),(2,1),(1,1)。

3.2 小波的选取

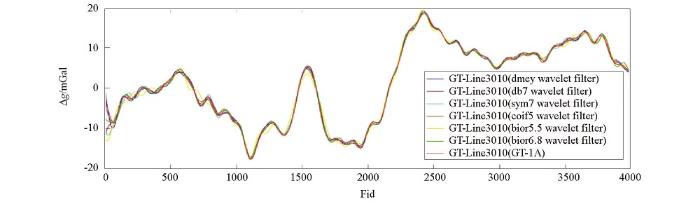
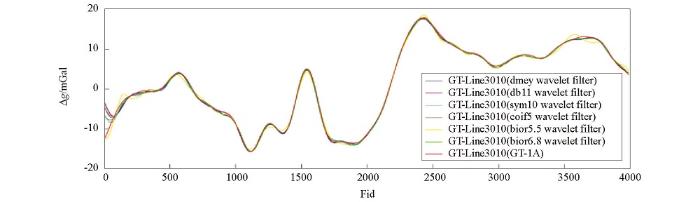
不同类型的小波,具有不同的特性(表2),滤波器小波的选取应从正交性、对称性、消失矩和正则性等多方面综合考虑。对于dbN、symN、coifN和biorNr.Nd小波系,随着小波阶数N的增大,小波具有更高的正则性^[24],相应也具有更高的频率分辨率。但处于不同频段的重力异常测量信号的信噪比不同,故滤波周期不同的滤波器对小波频率分辨率的需求也不尽相同。试验中,60 s滤波器选取dmey、db7、sym7、coif5、bior5.5和bior6.8小波,而100 s滤波器选取dmey、db11、sym10、coif5、bior5.5和bior6.8小波,对GT-1A系统获取的航空重力数据进行滤波试验研究。对于60 s和100 s滤波器小波的选取, dbN、symN小波系存在差异,而其他小波系则相同(在小波系现有小波中,所选用小波的频率分辨率已最高)。

首先,采用GT-1A系统数据处理软件对图6的原始未滤波数据进行60 s和100 s低通滤波处理,并将滤波结果作为近似标准;其次,采用本文设计的60 s和100 s小波包分解树,对GT-1A系统滤波结果分别进行小波包分解计算;最后,分别将分解的部分小波包系数(表3或表4:本行以下各行小波包节点系数)置“零”,再用剩余部分小波包系数(表3或表4:本行及以上各行小波包节点系数)进行重构计算,重构计算结果与GT-1A系统滤波结果的差值统计见表3和表4,表中数据为均方差值,单位为mGal。

表3 小波包重构计算结果与GT-1A系统滤波结果的差值统计(60 s低通滤波器)

Table 3 Difference statistics between the wavelet packet reconstruction’s computing result and GT-1A filtering result (60 s low-pass filter)

小波包节点	dmey小波	db7小波	sym7小波	coif5小波	bior5.5小波	bior6.8小波
(6,0)	0.3319	0.3847	0.3598	0.3638	0.3847	0.3802
(10,24)	0.2880	0.2296	0.2192	0.2409	0.2907	0.2349
(14,408)	0.2410	0.2274	0.2174	0.2318	0.2691	0.2591
(14,409)	0.2096	0.2310	0.2138	0.2329	0.2586	0.2569
(13,205)	0.2816	0.2348	0.2117	0.2299	0.2795	0.2377
(12,103)	0.2803	0.2366	0.2313	0.2114	0.2366	0.2519
(11,50)	0.2195	0.2165	0.2087	0.1935	0.2219	0.2131
(9,13)	0.7488	0.1221	0.1372	0.1124	0.1204	0.1092
(8,7)	0.0890	0.0538	0.0517	0.0482	0.0706	0.0523
(7,2)	0.0086	0.0316	0.0312	0.0191	0.0347	0.0289
(5,1)	3.8912×10^-4	8.8581×10^-4	8.7309×10^-4	4.3837×10^-4	0.0013	9.545×10^-4
(4,1)	3.2967×10^-4	2.7093×10^-4	2.7056×10^-4	2.7003×10^-4	2.7207×10^-4	2.7096×10^-4
(3,1)	3.1459×10^-4	2.5036×10^-4	2.4919×10^-4	2.5064×10^-4	2.5232×10^-4	2.4984×10^-4
(2,1)	2.7890×10^-4	2.0282×10^-4	2.0162×10^-4	2.0449×10^-4	2.0277×10^-4	2.0499 ×10^-4
(1,1)	1.8993×10^-4	9.1145×10^-11	4.2125×10^-11	1.6598×10^-7	7.4349×10^-11	1.2700×10^-11

表4 小波包重构计算结果与GT-1A系统滤波结果的差值统计(100 s低通滤波器)

Table 4 Difference statistics between the wavelet packet reconstruction’s computing result and GT-1A filtering result (100 s low-pass filter)

小波包节点	dmey小波	db11小波	sym10小波	coif5小波	bior5.5小波	bior6.8小波
(7,0)	0.6736	0.4610	0.5556	0.6279	0.5986	0.5803
(9,6)	0.1087	0.2421	0.2696	0.1314	0.2007	0.1795
(12,60)	0.0710	0.0913	0.1107	0.0596	0.1864	0.1679
(12,61)	0.1058	0.0569	0.0712	0.1003	0.1460	0.1106
(11,31)	0.1144	0.0657	0.1039	0.0951	0.1458	0.0866
(10,14)	0.1321	0.0305	0.0645	0.0336	0.1112	0.0527
(8,2)	0.0137	0.0165	0.0180	0.0166	0.0435	0.0332
(6,1)	3.6252×10^-4	4.5743×10^-4	4.8414×10^-4	4.5477×10^-4	0.0014	9.7659×10^-4
(5,1)	3.1777×10^-4	2.7884×10^-4	2.7928×10^-4	2.7893×10^-4	2.8253×10^-4	2.8021×10^-4
(4,1)	3.0947×10^-4	2.7023×10^-4	2.7035×10^-4	2.6972×10^-4	2.6975×10^-4	2.7044×10^-4
(3,1)	2.9291×10^-4	2.4962×10^-4	2.5092×10^-4	1.4942×10^-7	2.5072×10^-4	2.5129×10^-4
(2,1)	2.5544×10^-4	2.0668×10^-4	2.0458×10^-4	2.0489×10^-4	2.0926×10^-4	2.0485×10^-4
(1,1)	1.5082×10^-4	1.8804×10^-12	2.1780×10^-13	1.4942×10^-7	5.4468×10^-11	5.4468×10^-11

3.3 小波滤波试验

选用不同的正交或双正交小波(同前),采用本文研究、设计的60 s和100 s小波低通滤波器和本文提出的阈值量化处理方案,对图6所示的原始未滤波数据进行了低通滤波试验研究。

滤波结果如图8~19所示,表5和表6分别为60 s和100 s滤波结果与GT-1A系统滤波结果的差值统计,表中数据为均方差值,单位为mGal。

表5 小波滤波结果与GT-1A系统滤波结果的差值统计(滤波周期:60 s)

Table 5 Difference statistics between the wavelet filtering result and GT-1A filtering result (filtering period: 60 s)

小波	dmey	db7	sym7	coif5	bior5.5	bior6.8
方案1	0.4880	0.7049	0.6914	0.5549	2.5541	0.9831
方案2	0.2989	0.3970	0.3972	0.3222	0.9135	0.4799
方案3	0.2797	0.3971	0.3972	0.3204	0.9135	0.4776
方案4	0.3255	0.3971	0.4847	0.3204	0.9722	0.4928

表6 小波滤波结果与GT-1A系统滤波结果的差值统计(滤波周期:100 s)

Table 6 Difference statistics between the wavelet filtering result and GT-1A filtering result (filtering period: 100 s)

小波	dmey	db11	sym10	coif5	bior5.5	bior6.8
方案1	0.4168	0.3734	0.3999	0.4236	1.0332	0.5504
方案2	0.2176	0.2714	0.3125	0.2739	0.5091	0.3161
方案3	0.2262	0.2714	0.3125	0.2748	0.8593	0.3177
方案4	0.3362	0.2745	0.3125	0.2980	0.8860	0.3177

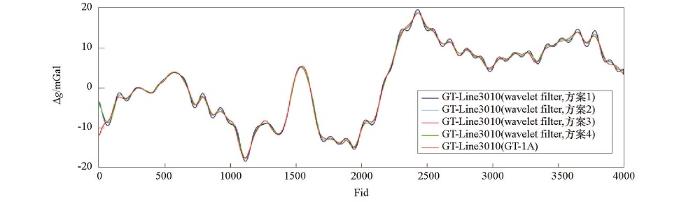
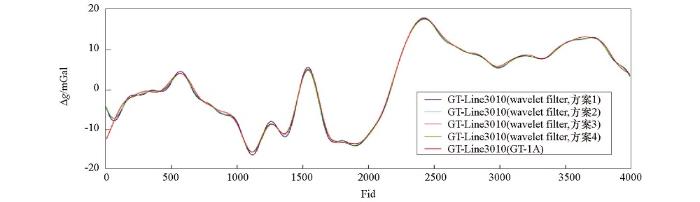
图8

图8 dmey小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.8 Airborne gravity free air anomaly of dmey wavelet and GT-1A 60 s filter

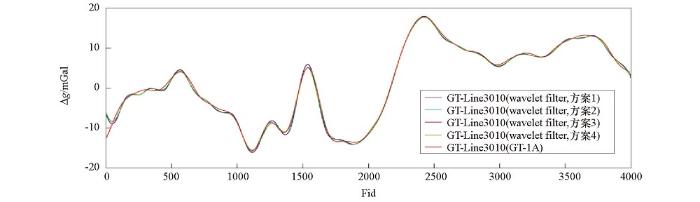
图9

图9 db7小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.9 Airborne gravity free air anomaly of db7 wavelet and GT-1A 60 s filter

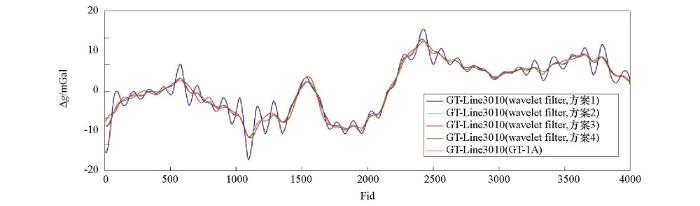
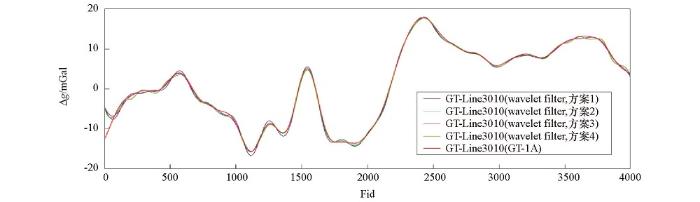
图10

图10 sym7小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.10 Airborne gravity free air anomaly of sym7 wavelet and GT-1A 60 s filter

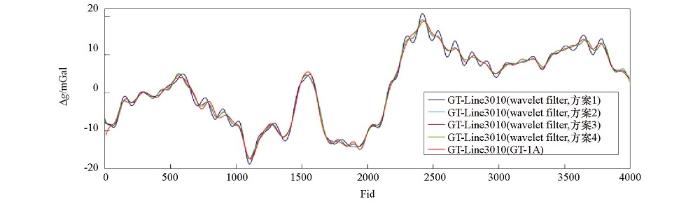
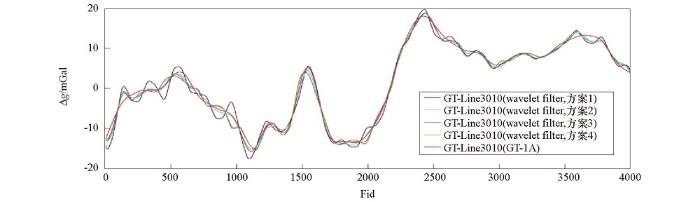
图11

图11 coif5小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.11 Airborne gravity free air anomaly of coif5 wavelet and GT-1A 60 s filter

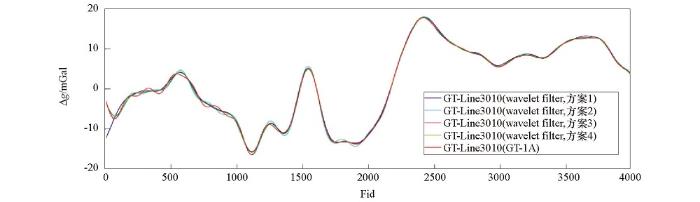
图12

图12 bior5.5小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.12 Airborne gravity free air anomaly of bior5.5 wavelet and GT-1A 60 s filter

图13

图13 bior6.8小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.13 Airborne gravity free air anomaly of bior6.8 wavelet and GT-1A 60 s filter

图14

图14 dmey小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.14 Airborne gravity free air anomaly of dmey wavelet and GT-1A 100 s filter

图15

图15 db11小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.15 Airborne gravity free air anomaly of db11 wavelet and GT-1A 100 s filter

图16

图16 sym10小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.16 Airborne gravity free air anomaly of sym10 wavelet and GT-1A 100 s filter

图17

图17 coif5小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.17 Airborne gravity free air anomaly of coif5 wavelet and GT-1A 100 s filter

图18

图18 bior5.5小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.18 Airborne gravity free air anomaly of bior5.5 wavelet and GT-1A 100 s filter

图19

图19 bior6.8小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.19 Airborne gravity free air anomaly of bior6.8 wavelet and GT-1A 100 s filter

3.4 结果分析

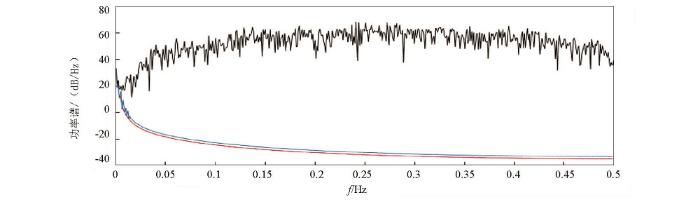
由表3、表4分析可知:① 试验中,所选取的正交或双正交小波(见表3和表4),按优化设计的小波包树分解后,能够精确完整重构;② 所选用小波,因频率分辨率和相位失真等因素的影响,引起重构计算结果误差;理想情况下,随着频率由低到高重构包含小波包系数的增加,重构计算结果误差会变小,小波滤波重构精度会提高。而滤波试验结果,随着频率由低到高重构包含小波包系数增加,重构计算结果误差出现局部波动,总体趋势和理想情况分析吻合。③由①和②进一步分析可知:本文小波包分解树的优化设计方案是可行的。

对GT-1A系统原始未滤波数据(图6)、及其经GT-1A系统软件60 s和100 s滤波获得的数据分别进行功率谱分析,结果如图20所示(黑色、蓝色和红色曲线分别为原始未滤波、及其GT-1A系统60 s和100 s滤波航空自由空间重力异常功率谱)。由图20分析可知:重力异常信号主要集中在小于 0.02 Hz低频段,在0~0.01 Hz频段的信噪比大于处于0.01~0.02 Hz频段的信噪比。

图20

图20 GT-1A系统原始未滤波、60 s和100 s滤波航空自由空间重力异常功率谱

Fig.20 Power spectrums of GT-1A raw unfiltered, 60 s and 100 s filtered airborne gravity free air anomaly

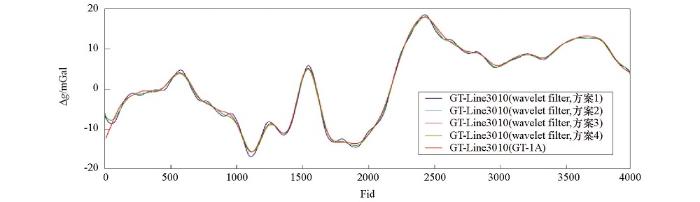
由表3或表4可以看出处于不同频带的小波包节点系数对滤波结果的影响,以60 s滤波器为例,对本文采用的阈值量化处理方案做进一步说明。方案1:保留低频系数,高频系数置“零”;方案2:在方案1基础上,对低频系数细化处理;节点(6,0)低频系数,以异常信号为主,对其进行平滑处理,抑制高频(相对)噪声干扰。节点(10,24)和(14,408)低频系数,噪声幅值远大于异常信号幅值,按估算比例压缩小波包系数幅值,降低高频(相对)噪声的影响,亦可采用通用阈值估计进行量化处理。方案3:在方案2基础上,对节点(14,409)高频(过度频带)系数,采用通用阈值估计进行量化处理;因小波包分解存在频率分辨率的问题,有可能造成频率失真,通过方案3弥补方案2的不足。因节点(14,409)小波包系数对应的频带宽度较“窄”,方案3对滤波效果的改善作用影响不大。方案4:在方案3基础上,对节点(13,205),(12,103),(11,50),(9,13)部分高频系数,采用通用阈值估计进行量化处理。对于高频系数,因信噪比极低,故阈值量化处理效果有限。综合以上分析可知:① 四种方案中,方案2或方案3滤波效果最佳;② 因在低频段,不同频带信噪比存在差异,频率越低,信噪比越大,故100 s滤波器的滤波效果好于60 s滤波器的滤波效果。

滤波试验结果图8~19、表5和表6也可进一步验证上述分析结果。通过对比分析可知:① 采用方案2~4的滤波效果好于采用方案1的滤波效果;② 采用方案2~4的滤波效果基本相同,其中滤波效果最佳的为方案2或方案3;③ 总体而言,100 s滤波器的滤波效果好于60 s滤波器的滤波效果。

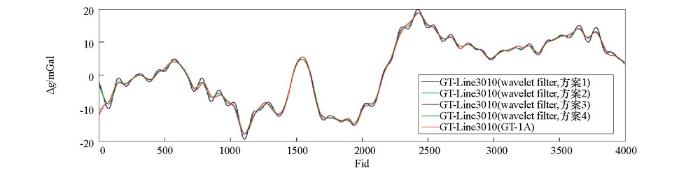
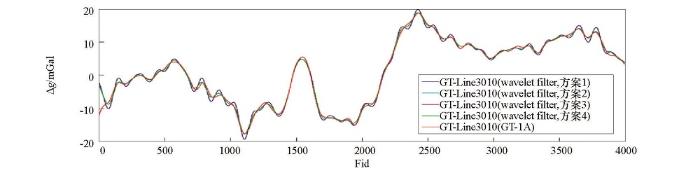
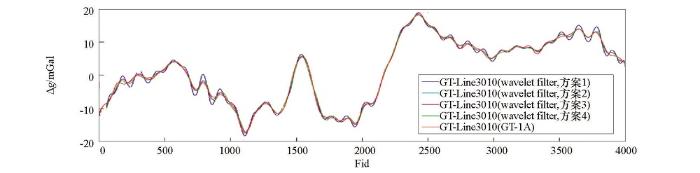
将滤波试验结果(最佳效果)按选用的小波归纳重新整理,不同小波60 s、100 s滤波结果分别如图21、图22所示,滤波结果与GT-1A系统滤波结果差值统计见表7。由图21、图22和表7分析可知:① 60 s小波滤波器:按滤波试验效果,选用小波的排列顺序依次为bior5.5、bior6.8、sym7、db7、coif5和 dmey小波,dmey小波滤波效果最佳(均方差值约为0.28 mGal);② 100 s小波滤波器:按滤波试验效果,选用小波的排列顺序依次为bior5.5、bior6.8、sym10、coif5、db11和 dmey小波,dmey小波滤波效果最佳(均方差值约为0.22 mGal)。

图21

图21 小波滤波器与GT-1A系统60 s滤波航空自由空间重力异常对比

Fig.21 Airborne gravity free air anomaly of wavelets and GT-1A 60 s filter

图22

图22 小波滤波器与GT-1A系统100 s滤波航空自由空间重力异常对比

Fig.22 Airborne gravity free air anomaly of wavelets and GT-1A 100 s filter

表7 小波滤波试验结果与GT-1A系统滤波结果的差值统计

Table 7 The difference between wavelet filtering and GT-1A filtering result and statistics

滤波周期 /s	小波	最大差值 /mGal	最小差值 /mGal	平均差值 /mGal	均方差值 /mGal	比较点数 (N)
60	dmey	0.6875	-0.6580	0.0035	0.2797	3000
	db7	0.8516	-0.8573	0.0030	0.3970	3000
	sym7	1.2614	-1.0514	-8.4227e-6	0.3972	3000
	coif5	0.8497	-0.7738	5.9950e-4	0.3204	3000
	bior5.5	2.5249	-2.3573	-0.0070	0.9135	3000
	bior6.8	1.3696	-1.3667	0.0042	0.4776	3000
100	dmey	0.1578	-0.4360	-0.1747	0.2176	3000
	db11	0.3647	-0.6425	-0.1758	0.2714	3000
	sym10	0.5981	-0.8946	-0.1740	0.3125	3000
	coif5	0.3847	-0.6568	-0.1783	0.2739	3000
	bior5.5	0.8561	-1.2599	-0.2012	0.5091	3000
	bior6.8	0.4365	-0.7784	-0.1820	0.3161	3000

滤波试验效果与选用小波的频率分辨率和对称性有关,根据所选小波频率分辨率高低,再考虑小波的对称性,综合判断小波滤波试验效果。在滤波试验选用的小波中,db7和db11小波无对称性,sym7、sym10和coif5小波均具有准对称性,而dmey、bior5.5和bior6.8小波才具有完全对称性。由表5和表6中方案1的滤波效果可判断出所选用小波频率分辨率的高低,亦可按小波频率分辨率定义计算比较^[24]。60 s滤波试验中,选用的coif5和 dmey小波频率分辨率较高;100 s滤波试验中,选用的coif5、dmey、sym10和db11小波频率分辨率较高。综合小波频率分辨率和对称性二者因素,可判断在60 s和100 s滤波试验中,选用dmey小波的滤波效果为最佳,这与试验结果与GT-1A结果差值统计表5和表6数据相吻合,也与相关文献的研究结果一致^[24]。

4 结论

1) 基于小波包系数频率顺序,本文提出的小波包分解树的优化设计方案是可行的。根据滤波器的截止频率(滤波周期的倒数)、估算的分解层次对应的信号频率范围和小波包系数频率由小到大节点的排列顺序,优化设计小波包分解树,为小波滤波器的设计奠定基础。

2) 选用正交或双正交小波,本文研究、设计的小波低通滤波器,以及提出的阈值处理方案是可行的。滤波试验:60 s和100 s滤波结果与GT-1A系统滤波结果的均方差值分别达到约0.28 mGal和0.22 mGal,获得与GT-1A系统几乎同样满意的滤波效果。

3) 在低频段,处于不同频带(节点)的小波包系数信噪比不同,应采用不同的方案进行量化处理。在本文提出的4种阈值量化处理方案中,方案2或方案3的滤波效果最佳(相对GT-1A系统滤波结果)。

4) 滤波效果与选用小波的频率分辨率和对称性有关。在滤波试验选中的不同类型的小波中,选用dmey小波的滤波器滤波效果最佳(相对GT-1A系统);选用bior5.5小波的滤波器,方案2相较于方案1的滤波效果改善幅度相对最大(见表5)。

与离散Meyer小波不同,B样条小波是双正交的、局部紧支撑、且同样也具有良好的对称性和平滑性。如何构造出比dmey小波具有更高频率分辨率的B样条小波,进一步提高小波滤波器的滤波效果,有待于后续深入研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

孙中苗

航空重力测量理论、方法及应用研究

[D]. 郑州:解放军信息工程大学, 2004.

Sun Z

Theory, Methods and applications of airborne gravimetry

[D]. Zhengzhou: PLA Information Engineering University, 2004.

[2]

郭志宏, 罗锋, 安战锋 .

航空重力数据窗函数法FIR低通数字滤波试验

[J]. 物探与化探, 2007,31(6):568-571.

Guo Z

, Luo

, An Z

Experiment researches on FIR low pass digital filters based on window functions of airborne gravity data

[J]. Geophysical and Geochemical Exploration, 2007,31(6):568-571.

[3]

郭志宏

航空重力数据测量处理方法技术研究[R].“百人计划”项目研究报告

北京:中华人民共和国国土资源部, 2008.

Guo Z

The method and technology research of airborne gravity survey and data processing[R]. “Hundred People Plan” Project Research Report

Beijing: Ministry of Land and Resources of the People’s Republic of China, 2008.

[4]

王静波

航空重力测量数据处理方法技术研究

[D].北京:中国地质大学(北京), 2010.

Wang J

Methodologies and technology of data processing for airborne gravimetry

[D]. Beijing: China University of Geosciences(Beijing), 2010.

[5]

熊盛青, 周锡华, 郭志宏 , 等. 航空重力勘探理论方法及应用[M]. 北京: 地质出版社, 2010.

Xiong S

, Zhou X

, Guo Z

, et al. Theory, methods and application of the airborne gravity prospecting[M]. Beijing: Geological Publishing House, 2010.

[6]

王静波, 熊盛青, 郭志宏 , 等.

航空重力异常估计方法研究

[J]. 物探与化探, 2011,35(4):493-498.

Wang J

, Xiong S

, Guo Z

, et al.

Research on methods of estimating airborne gravity anomaly

[J]. Geophysical and Geochemical Exploration, 2011,35(4):493-498.

[7]

郭志宏, 罗锋, 王明 , 等.

航空重力数据无限脉冲响应低通数字滤波器设计与试验研究

[J]. 地球物理学报, 2011,54(8):2148-2153.

Guo Z

, Luo

, Wang

, et al.

The design and experiment of IIR low pass digital filters for airborne gravity data

[J]. Chinese J. Geophys., 2011,54(8):2148-2153.

[8]

王静波, 熊盛青, 郭志宏 , 等.

航空重力数据Kalman滤波平滑技术应用研究

[J]. 地球物理学进展, 2012,27(4):1717-1722.

Wang J

, Xiong S

, Guo Z

, et al.

Kalman smoothing for airborne gravity data

[J]. Progress in Geophysics, 2012,27(4):1717-1722.

[9]

罗锋, 郭志宏, 骆遥 , 等.

航空重力数据的等波纹FIR 低通滤波试验

[J]. 物探与化探, 2012,36(5):856-860.

Luo

, Guo Z

, Luo

, et al.

Experimental researches on fir lowpass filter based on equiripple

[J]. Geophysical and Geochemical Exploration, 2012,36(5):856-860.

[10]

阮秋琦

. 数字图象处理学[M]. 北京: 电子工业出版社, 2001.

[本文引用: 4]

Ruan Q

Digital image processing[M]. Beijing: Publishing House of Electronics Industry, 2001.

[本文引用: 4]

[11]

罗锋, 郭志宏, 王明 , 等.

基于DB小波阈值去噪的航空重力数据试验

[J]. 物探与化探, 2013,37(4):645-654.

Luo

, Guo Z

, Wang

, et al.

Experimental reseaches on the theshold of airbone gravity data denoising based on DB wavelet transfom

[J]. Geophysical and Geochemical Exploration, 2013,37(4):645-654.

[12]

柳林涛, 许厚泽 .

航空重力测量数据的小波滤波处理

[J]. 地球物理学报, 2004,47(3):490-494.

Liu L

, Xu H

Wavelets in airborne gravimetry

[J]. Chinese J. Geophys., 2004,47(3):490-494.

[13]

孙中苗, 翟振和 .

航空重力测量数据的小波阈值滤波

[J]. 武汉大学学报:信息科学版, 2009,34(10):1222-1225.

Sun Z

, Zhai Z

Filtering of the airborne gravity data by wavelet thresholding

[J]. Geomatics and Information Science of Wuhan University, 2009,34(10):1222-1225.

[14]

李肃义, 林君, 阳贵红 , 等.

电性源时域地空电磁数据小波去噪方法研究

[J]. 地球物理学报, 2013,56(9):3145-3152.

Li S

, Lin

, Yang G

, et al.

Ground-airborne electromagnetic signals de-noising using a combined wavelet transform algorithm

[J]. Chinese J. Geophys. , 2013,56(9):3145-3152.

[15]

章浙涛, 朱建军, 匡翠林 , 等.

小波包多阈值去噪法及其在形变分析中的应用

[J]. 测绘学报, 2014,43(1):13-20.

[本文引用: 7]

Zhang Z

, Zhu J

, Kuang C

, et al.

Multi-threshold wavelet packet de-noising method and its application in deformation analysis

[J]. Acta Geodaetica et Cartographica Sinica, 2014,43(1):13-20.

[本文引用: 7]

[16]

武粤, 孟小红, 李淑玲 .

小波分析及其在我国地球物理学研究中的应用进展

[J]. 地球物理学进展, 2012,27(2):750-760.

, Meng X

, Li S

Wavelet analysis and its application in geophysics of China

[J]. Progress in Geoophys., 2012,27(2):750-760.

[17]

Misiti

, Misiti

, Oppenheim

, et al.

Wavelet toolbox for use with Matlab (User’s Guide Version 1)

[M]. The MathWorks, Inc., 1996.

[本文引用: 9]

[18]

关履泰

. 小波方法与应用[M]. 北京: 高等教育出版社, 2007.

Guan L

Methods of wavelets and their applications [M]. Beijing: Higher Education Press, 2007.

[19]

Goswami J

, Chan A

Fundamentals of wavelets: theory, algorithms, and applications

[M]. John Wiley & Sons, 2011.

[20]

吴继忠, 花向红, 高俊强 .

基于小波包分解的结构自振特征提取及多路径误差分离

[J]. 武汉大学学报·信息科学版, 2010,35(4):486-490.

Wu J

, Hua X

, Gao J

Feature extraction of structure natural vibration and multipath separation based on wavelet packet decomposition

[J]. Geomatics and information Science of Wuhan Univers, 2010,35(4):486-490.

[21]

阎妍, 行鸿彦 .

基于小波包多阈值处理的海杂波去噪方法

[J]. 电子测量与仪器学报, 2018,32(8):172-178.

Yan

, Xing H

Sea clutter de-noising based on wavelet packet multi-threshold method

[J]. Journal of Electronic Measurement and Instrumentation, 2018,32(8):172-178.

[22]

吕楠楠, 苏淑靖, 翟成瑞 .

改进小波包阈值算法在振动信号去噪中的应用

[J]. 探测与控制学报, 2018,40(1):119-123.

Lyu N

, Su S

, Zhai C

Application of improved wavelet packet threshold algorithm in aibration signal denoising

[J]. Journal of Detection & Control, 2018,40(1):119-123.

[23]

Katunin

B-spline wavelet packets and their application in the multiresoluton non-stationary signal processing

[J]. Scientifc Problems of Machines Operation and Maintenance, 2010,163(3):103-115.