基于非结构化网格的重力梯度张量反演

doi:10.11720/wtyht.2020.2256

基于非结构化网格的重力梯度张量反演

黄天统, 彭新发, 朱自强

核工业二三〇研究所,湖南长沙 410007

Inversion of gravity gradient tensor based on unstructured grids

HUANG Tian-Tong, PENG Xin-Fa, ZHU Zi-Qiang

Changsha Uranium Geology Research Institute, Changsha 410007,China

责任编辑: 王萌

收稿日期: 2018-06-28 修回日期: 2019-08-13 网络出版日期: 2020-02-20

Received: 2018-06-28 Revised: 2019-08-13 Online: 2020-02-20

作者简介 About authors

黄天统(1991-),男,硕士,工程师,主要从事重磁勘探及重磁正反演工作。Email:735084175@qq.com 。

摘要

由于重力梯度张量是重力位的二阶导数,与传统的重力测量相比,重力梯度张量具有更高的分辨率,并且重力梯度张量具有5个相互独立的分量,包含了更多的地下空间信息和密度信息,因此将重力梯度张量数据应用到反演中可以得到较好的反演结果。非结构化网格具有很强的几何适应性,能够较好地拟合复杂异常体的边界,通过非结构化网格对反演目标区域进行离散,可以降低剖分误差,从而提高计算精度。为了降低反演过程中的多解性问题,将地球物理反问题的广义正则化目标函数应用于基于非结构化网格的三维重力梯度张量反演中,推导了相关公式,实现了各分量的独立反演,并阐述了深度加权函数在反演过程中的作用。为了充分利用重力梯度张量各分量所携带的密度、空间信息,将5个独立的分量进行了联合反演,反演结果表明,基于非结构化网格的三维重力梯度张量反演能够较好地反映地下异常源的物性分布和赋存位置。通过与长方体网格反演结果对比,本反演方法突出了非结构化网格反演的优越性;最后,通过较复杂组合模型的计算证实了方法的实用性。

关键词： 非结构化网格 ; 重力梯度张量 ; 反演

Abstract

Gravity gradient tensor is the second derivatives of gravitational field. Compared with the traditional gravitational exploration, gravity gradient tensor can reach a better resolution. Gravity gradient tensor has 5 independent components, so they can contain more geological information. Therefore, gravity gradient tensor can be used to recover the causative bodies in the subsurface with high accuracy. Due to strong adaptability and flexibility of the unstructured grid, it can smoothly approximate the irregular and complex boundaries of anomalous source. Compared with the structured grid, the unstructured grid can provide researchers with more accurate discretization and calculation with less computation time. In order to reduce the ambiguity of the inversion, the authors chose to jointly and simultaneously invert all gravity gradient components based on tetrahedron grids with the help of the so called generalized objective function which is widely used in geophysical inverse problems. The authors applied the algorithm to each gravity tensor component at the beginning to ensure that the depth weighting function makes a difference in the inversion. It turns out that the depth weighting function works well. To explore all components of the gravity gradient tensor as much as possible, the authors described the joint-inversion in detail in this paper. The inversion results show that 3D inversion of gravity gradient tensor based on unstructured grids can obtain the position of causative bodies in the subsurface and the density distribution. Based on a comparison with rectangular grid inversion results, the authors highlighted the advantages of unstructured grid inversion. And the practicability of the method was verified through two synthetic models.

Keywords： unstructured grids ; gravity gradient tensor ; inversion

PDF (3191KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄天统, 彭新发, 朱自强. 基于非结构化网格的重力梯度张量反演. 物探与化探[J], 2020, 44(1): 132-140 doi:10.11720/wtyht.2020.2256

HUANG Tian-Tong, PENG Xin-Fa, ZHU Zi-Qiang. Inversion of gravity gradient tensor based on unstructured grids. Geophysical and Geochemical Exploration[J], 2020, 44(1): 132-140 doi:10.11720/wtyht.2020.2256

0 引言

作为一种高精度的地球物理勘探方法,在实际勘探过程中重力梯度张量测量的是重力位的二阶导数。与传统的重力勘探相比,重力梯度张量测量对地下介质密度变化反映更加灵敏,具有更好的抗干扰能力,能够更加直接地反映地下密度异常体的水平边界位置^[1,2,3]。在国外,重力梯度张量勘探技术已经较为广泛地应用于海洋领域、航空领域以及卫星重力领域。

结构化网格是指网格区域内所有的内部点都具有相同的毗邻单元。由于非结构网格具有生成速度快、网格的数据结构简单、网格的质量好等优点^[4],广泛地应用于形状规则的物体剖分。但是随着计算机技术的飞速发展,结构化网格的弊端越来越明显,比如:待剖分物体的几何形状越来越复杂,结构化网格剖分带来了的剖分误差也越来越大,并且节点和网格单元在高质量情况下不能合理地呈梯度状分布在剖分的网格中^[5]。

与结构化网格相比,非结构化网格弥补了其不能解决所有形状和任意连通区域网格剖分的不足;对于网格单元和节点的编号,非结构化网格并没有固定的规则,两个相邻单元格编号对应的网格单元不一定相邻,这样使得非结构化网格能够十分方便的控制单元和节点的分布,具有很强的适应性,能够更好地剖分复杂模型。

在地球物理数值模拟过程中,高效地拟合场源模型及地形分布将更加有利于模型的计算,非结构化网格与生俱来的优势使其广泛地应用于地球物理数值模拟中。汤井田^[6]、任政勇^[7]在基于非结构化网格的情况下实现了2.5维的自适应有限元直流电阻率的正演模拟;孙丽影^[8]、刘长生^[9]、童孝忠^[10]通过非结构化网格进行局部加密完成了大地电磁二维、三维有限元数据模拟;赵晓博利用Delaunay三角化实现了中心回线瞬变电磁2.5维的正演模拟;曾思红^[11]、曹书锦^[12]利用有限单元法在非结构化网格下对重力梯度张量进行了二维、三维正演,Jahandari^[13]则是运用有限体积法实现了基于非结构化网格的二维、三维的重力高精度正演模拟,取得了较好的效果;Okabe^[14]推导了任意多边形和多面体网格下的重磁一阶、二阶导数的二维、三维解析表达式,具有很高的计算精度。

目前,对于重力梯度张量数据反演,大多都是基于长方形或者长方体等结构化网格进行的,但由于结构化网格的几何适应能力差,在较复杂地质体或地形的情况下会带来较大的剖分误差,从而使得反演效果有所下降。与结构化网格相比,非结构化网格能够减少模型的剖分误差,更好地拟合地下密度异常体的分布和地表地形的变化,因此,研究基于非结构化网格的重力梯度张量反演算法,可以提高重力梯度张量反演过程中的计算精度。现在,根据非结构化网格进行的地球物理反演主要还是基于二维三角形网格,elièvre^[15]、吉日嘎拉图^[16]利用地震初至波完成了二维慢度的反演,并完成了非结构化网格重震二维联合反演,使得反演的纵横向分辨率都很高,降低了反演结果的多解性问题。对于位场三维非结构化网格的反演,国内外文献中很少有涉及到。

1 正反演算法

1.1 基于非结构化网格重力梯度张量正演算法

重力梯度张量是重力位的二阶导数,在笛卡尔坐标系下,根据牛顿万有引力定律,一个剩余密度为ρ,观测点为P(p₀,q₀,r₀),位于Q(p,q,r)地下异常体ν在地下产生的重力位V有:

(1)

V = - G \int_{V} ρ u d ν,

其中:G为万有引力常量,u=-(x²+y²+z²)^-1^/²,x=p-p₀、y=q-q₀、z=r-r₀。则重力梯度张量表达式写成矩阵形式:

(2)

Γ = [\begin{array}{l} \frac{\partial^{2} V}{\partial x^{2}} & \frac{\partial^{2} V}{\partial x \partial y} & \frac{\partial^{2} V}{\partial x \partial z} \\ \frac{\partial^{2} V}{\partial y \partial x} & \frac{\partial^{2} V}{\partial y^{2}} & \frac{\partial^{2} V}{\partial y \partial z} \\ \frac{\partial^{2} V}{\partial z \partial x} & \frac{\partial^{2} V}{\partial z \partial y} & \frac{\partial^{2} V}{\partial z^{2}} \end{array}] = [\begin{array}{l} V_{xx} & V_{xy} & V_{xz} \\ V_{yx} & V_{yy} & V_{yz} \\ V_{zx} & V_{zy} & V_{zz} \end{array}],

其中:Γ表示全重力梯度张量。重力梯度张量共有9个分量,由于在无源空间里重力的旋度和散度都为0,有V_xx+V_yy+V_zz=0,V_yx=V_xy,V_zx=V_xz,V_zy=V_yz,因此重力梯度张量中只有5个独立分量V_xx、V_xy、V_xz、V_yz、V_zz。

重力位在k方向上的一阶导数:

(3)$V_{k}=-\bigtriangledown(V)·k,$

其中:k是k方向法向量:k^T=(k_x,k_y,k_z)或者k^T=(cos (x,k),cos (y,k),cos (z,k))。

将式(1)带入式(3)得:

(4)$V_{k}=G\int_{V}\bigtriangledown(\rho u)·kdv。$

引入另一个方向向量l:l^T=(l_x,l_y,l_z),对于不同的重力梯度张量分量,k、l的方向余弦取值如表1所示。对V_k求在l方向求导,得到重力位的二阶导数:

(5)$V_{kl}=-G\int_{v}\bigtriangledown[\bigtriangledown(\rho u)·k]ldv。$

表1 方向余弦的取值与重力梯度张量各分量的关系

Table 1 the relationship between the value of direction cosine and the gravity gradient tensor components

重力梯度张量	k_x	k_y	k_z	l_x	l_y	l_z
V_xx	1	0	0	1	0	0
V_yy	0	1	0	0	1	0
V_zz	0	0	1	0	0	1
V_xy	1	0	0	0	1	0
V_yz	0	1	0	0	0	1
V_xz	0	0	1	1	0	0

新窗口打开| 下载CSV

对式(5)利用散度定理得:

(6)$V_{kl}=-G\int_{s}l^{T}n·\bigtriangledown(\rho u)·kdS,$

其中:S为地下异常体ν的表面,n为面S的法向量,指向异常体外部。

在四面体网格的形式下,式(6)的积分可以写成每个网格的积分总和的形式:

(7)

V_{kl} = Gρ \sum_{i} l^{T} n_{i} K_{i},

其中:

(8)$K_{i}=-\int_{S_{i}}\bigtriangledown(u)kdS。$

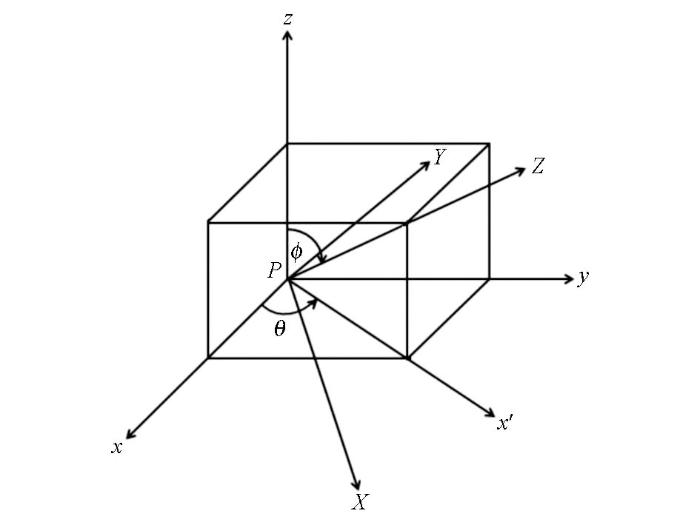
为了快速地求解出面S_i上K_i的值,采用了坐标选择的方法。旋转分为两步:首先,以z轴为中心逆时针^[15]旋转xOy平面(笛卡尔坐标系),直到x方向与面的外法向量在xOy平面上的投影平行,旋转的角度为θ,得到最终的坐标系统(X,Y,Z)。然后,以Y轴为中心逆时针选择x'Oz 轴,直到z方向与面的外法向量平行,旋转的角度为ϕ,得到最终的坐标系统(X,Y,Z),如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 面坐标系统旋转示意

Fig.1 The surface rotation of the Cartesian system

坐标的旋转转换可以写成:

(9)

[\begin{array}{l} X \\ Y \\ Z \end{array}] = [\begin{array}{l} \cos ϕ & 0 & - \sin ϕ \\ 0 & 1 & 0 \\ \sin ϕ & 0 & \cos ϕ \end{array}] [\begin{array}{l} \cos θ & \sin θ & 0 \\ - \sin θ & \cos θ & 0 \\ 0 & 0 & 1 \end{array}] [\begin{array}{l} x \\ y \\ z \end{array}]

其中:0≤θ<2π,0≤ϕ≤π。通过旋转,面S_i上的3个顶点的Z值相等,面S_i的外法向量n_i可以写成:

(10)

{n^{T}}_{i} = (\sin ϕ \cos θ, \sin ϕ \sin θ, \cos ϕ),

在(X,Y,Z)坐标系统下,式(8)可以写成:

(11)

K_{i} = - \underset{S_{i}}{\int \int} \frac{M_{x} \cdot X + M_{y} \cdot Y + M_{z} \cdot Z}{(X^{2} + Y^{2} + Z^{2})^{3 / 2}} d X d Y,

其中:

(12)

\begin{matrix} \{\begin{array}{l} M_{X} = (k_{x} \cos θ + k_{y} \sin θ) \cos ϕ - k_{z} \sin ϕ \\ M_{Y} = - k_{x} \sin θ + k_{y} \cos θ \\ M_{Z} = (k_{x} \cos θ + k_{y} \sin θ) \sin ϕ + k_{z} \cos ϕ \end{array} \end{matrix}

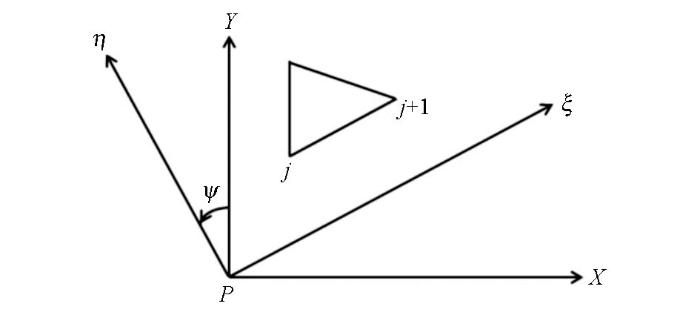
通过对S_i面上的每条边进行二维坐标旋转,可以将式(11)的面积分转换为线积分。以原点为中心,逆时针旋转X轴、Y轴,直到X方向与S_i面上的j边重合,得到新的坐标系统(ξ,η)旋转的角度为ψ,0≤ψ<2π,如图2所示。坐标的旋转转换可以写成:

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 边坐标系统旋转示意

Fig.2 The edge rotation of the Cartesian system

(13)

[\begin{array}{l} ξ \\ η \end{array}] = [\begin{array}{l} \cos ψ & \sin ψ \\ - \sin ψ & \cos ψ \end{array}] [\begin{array}{l} X \\ Y \end{array}],

通过旋转,S_i面上j边的两个端点的η值相等,j边的法向量s_j为:

(14)

{s^{T}}_{j} = (- \sin ψ, \cos ψ),

那么,式(11)就可以写成:

(15)

K_{i} = \sum_{j} L_{j} (i),

从而得到:

(16)

\begin{array}{l} L_{j} (i) = (M_{X} \sin ψ - M_{Y} \cos ψ) \int_{ξ_{j}}^{ξ_{j + 1}} u d ξ + & M_{Z} \cos ψ \int_{ξ_{j}}^{ξ_{j + 1}} u YZ (X^{2} + Z^{2})^{- 1} d ξ, \end{array}

对式(16)求积分得到:

(17)

\begin{array}{l} L_{j} (i) = {(M_{X} \sin ψ - M_{Y} \cos ψ) \cdot & \ln [ξ + (ξ^{2} + η^{2} + Z^{2})^{1 / 2}] \cdot \\ M_{Z} \cdot \arctan \frac{- ξη + (η^{2} + Z^{2}) \tan ψ}{Z \cdot (ξ^{2} + η^{2} + Z^{2})^{1 / 2}}}_{ξ_{j}}^{ξ_{j + 1}}, \end{array}

最终得到重力位二阶导数的表达式:

(18)

V_{kl} = Gρ \sum_{i} \sum_{j} l^{T} n_{i} L_{j} (i) 。

如果Z或者cos ψ的值为0,则式(17)的后面一项为0,但是此时式(17)的第一项的值不一定一直存在,例如η和Z的值都趋近于0,且ξ不为正数。当ξ_j和ξ_j₊₁都为负时,通过式(19)可以避免,对于其他情形可用一个较小的值代替。

(19)

\begin{array}{l} \ln [ξ + (ξ^{2} + η^{2} + Z^{2})^{1 / 2}]_{ξ_{j}}^{ξ_{j + 1}} = & - \ln [(ξ^{2} + η^{2} + Z^{2})^{1 / 2} {- ξ]}}_{ξ_{j}}^{ξ_{j + 1}} 。 \end{array}

1.2 反演的基本理论

由于重力梯度张量反问题是一个不适定问题,为了得到一个稳定的可行解,李耀国等人^[16]在吉洪诺夫正则化理论的基础上提出了一个能够广泛应用于地球物理反问题的广义目标函数,其中数据拟合函数为:

(20)

\begin{array}{r} ϕ_{d} (m) & = \overset{N}{\sum_{i = 1}} (\frac{d_{i}^{obs} - F (m)}{ε_{i}}) & = ‖ W_{d} (d^{obs} - F (m)) ‖^{2}, \end{array}

其中:W_d=diag{1/ε₁,…,1/ε_N},ε_i为第i个观测数据的标准差。通常假设实际数据的误差是相互独立且满足高斯分布的,实测得到重力梯度张量数据d^obs=F(m)+δ,δ表示的是观测点上的随机噪声。由于随机噪声δ是满足高斯分布N(0,ε²)的,ε为观测数据的标准差。根据最小二乘拟合,那么反演最终的数据拟合差为:

(21)

\begin{array}{l} misfit = ϕ_{d} = \overset{N}{\sum_{i = 1}} {(\frac{F (m) + δ_{i} - F (m)}{ε_{i}})}^{2} & = \overset{N}{\sum_{i = 1}} {(\frac{δ_{i} - 0}{ε_{i}})}^{2} = \frac{N ε^{2}}{ε^{2}} = N, \end{array}

其中:N为测点数。

在最小化目标函数的过程中,在目标函数中引入的模型目标函数为:

(22)

\begin{array}{l} ϕ_{m} (m) = α_{s} \int_{v} m - m_{ref})^{2} d ν + α_{x} \int_{v} {(\frac{\partial (m - m_{ref})}{\partial x})}^{2} d ν + \\ α_{y} \int_{v} {(\frac{\partial (m - m_{ref})}{\partial y})}^{2} d ν + α_{z} \int_{v} {(\frac{\partial (m - m_{ref})}{\partial z})}^{2} d ν, \end{array}

因此,根据式(21),在最小化模型目标函数时,数据拟合项的最终拟合差是满足 $ϕ_{d}^{*}$ =N的。将式(22)写成范数的形式有:

(23)

\begin{array}{l} ϕ_{m} (m) = α_{s} ‖ W_{s} (m - m_{ref}) ‖^{2} + \\ α_{x} ‖ W_{x} (m - m_{ref}) ‖^{2} + α_{y} ‖ W_{y} (m - m_{ref}) ‖^{2} + \\ α_{z} ‖ W_{z} (m - m_{ref}) ‖^{2} \end{array}

其中:α_s、α_x、α_y、α_z为每项的加权系数,W_s为粗糙度矩阵,W_x、W_y、W_z分别为x、y、z三个方向上的差分算子。令:

(24)

{W^{T}}_{m} W_{m} = α_{s} {W^{T}}_{s} W_{s} + α_{x} {W^{T}}_{x} W_{x} + α_{y} {W^{T}}_{y} W_{y} + α_{z} {W^{T}}_{z} W_{z},

然而,在非结构化网格下,差分矩阵W_x、W_y、W_z的求解不能像在结构化网格情况下那样简单的求解。为了解决差分矩阵的计算问题,在Lelièvre^[15]提出的二维求解W_m的计算方法基础上进行衍生,得到三维情况下两个相邻网格W_m的计算方法。

(25)

W_{m} = \frac{\sqrt[3]{(V_{1} + V_{2}) / 2}}{R},

其中:V₁、V₂为两个相邻四面体网格的体积,R为两个四面体网格的中心距离。

结合数据拟合函数式(1)和模型目标函数式(4)可以得到广义的反演目标函数:

(26)

\begin{array}{r} ϕ (m) & = ϕ_{d} (m) + a ϕ_{m} (m) & = ‖ W_{d} (d^{obs} - F (m)) ‖^{2} + & a ‖ W_{m} (m - m_{ref}) ‖^{2}, \end{array}

其中:正则化参数a的取值应该满足ϕ_d(a)= $ϕ_{d}^{*}$ =N(N是测点数),因为此时的a是能够很好地平衡数据目标函数与模型目标函数,这样在反演过程中求解出来模型参数m的值既能够使得模型目标最小,又能够使得正演数据合理拟合观测数据。

1.3 深度加权函数

为了使得反演结果能够反演出深度上的结构,提高深度方向上的分辨率,李耀国等人^[19]引入了一个深度加权函数来减小核矩阵在深度方向上的衰减:

(27)

W (z) = \frac{1}{(z + z_{0})^{β / 2}},

其中:z是网格单元的中心埋深,z₀是个常数,β是一个接近于3的常数,在已知网格剖分方式和观测面的高度后,通过调节z₀和β的值,来尽可能地减少核函数在深度方向上的衰减,从而使得反演结果能够准确地分布在对应的深度上。式(24)结合深度加权函数得到

(28)

{W^{T}}_{m} W_{m} = W^{T} {W^{T}}_{m} W_{m} W 。

将深度加权函数结合式(22)得到带深度加权的模型目标函数:

(29)

ϕ_{m} (m) = ‖ W_{m} (m - m_{ref}) ‖^{2}

1.4 多分量联合反演

多分量的联合反演的目标函数只需要对式(26)中的数据拟合项进行适当的修改,即将各个分量的数据拟合项结合起来形成一个总的数据拟合项。结合模型目标函数,对于重力梯度张量多分量联合反演的目标函数可以写成:

(30)

\begin{array}{l} ϕ (m) = \sum_{α, β} γ_{αβ} ‖ W_{d}^{αβ} (d_{αβ}^{obs} - G_{αβ} m) ‖^{2} + & a ‖ W_{m} (m - m_{ref}) ‖^{2}, \end{array}

$\begin{array}{l} α, β = x, y, z \end{array}$

式中:γ_αβ是不同分量数据拟合的权系数, $d_{αβ}^{obs}$ 为不同分量的观测数据,G_αβ代表不同分量的雅克比矩阵。

2 算法验算

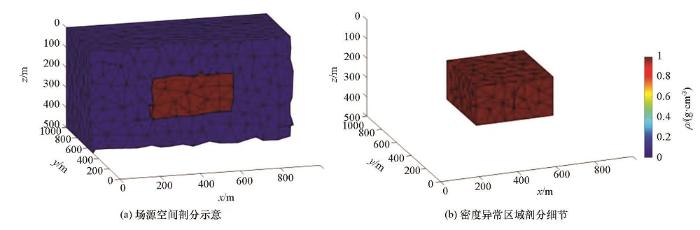
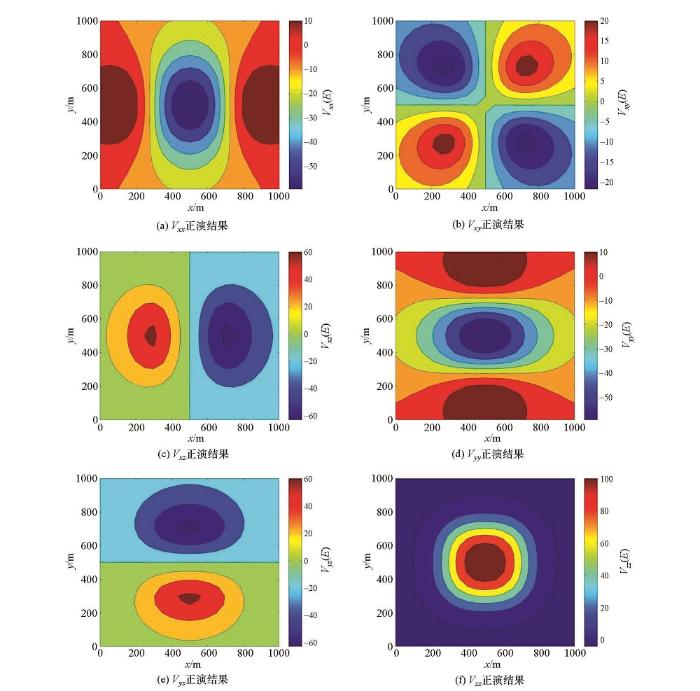
图3所示为单个长方体模型,场源空间大小为1 000 m×1 000 m×500 m,其内埋藏着一个大小400 m×400 m×200 m的存在密度异常的长方体,长方体顶部埋深为150 m,底部埋深为350 m,水平中心位置在地表的投影坐标为(500 m,500 m),长方体剩余密度为1.0 g/cm³,观测位置位于地表,x、y方向测线的长度1 000 m、点距50 m。根据已剖分的网格单元,应用前文推导的公式计算出来的重力梯度张量各分量的正演结果如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 单个长方体模型非结构化网格剖分示意

Fig.3 The schematic diagram of a single rectangular model using unstructured meshing

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 单个长方体模型重力梯度张量正演结果

Fig.4 Forward results of the single rectangular model

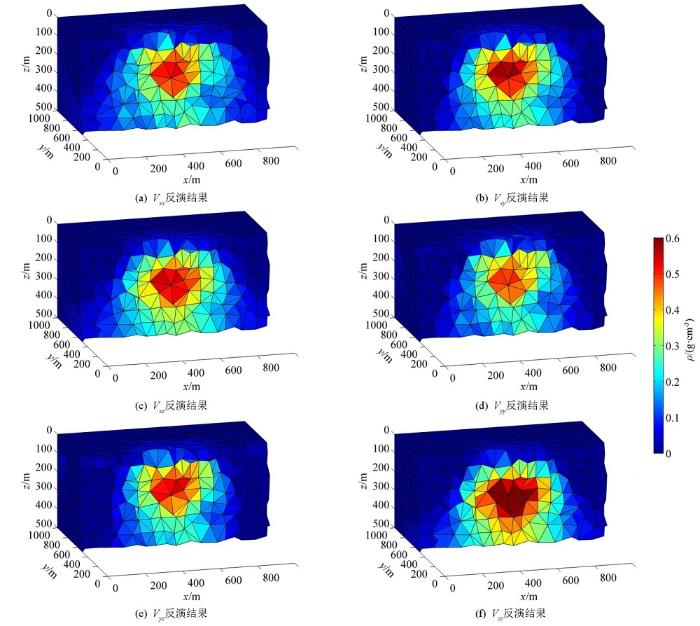
从图4可以看出,重力梯度张量各个分量的正演结果都能够明显地反映地下密度异常体的边界位置。V_xy的4个极值点对应了长方体4个顶点的水平投影位置;V_xx、V_yy的极小值位置对应的是长方体水平中心位置,并且等值线变化最密集的部分正好是长方体的4条边界位置;V_xz、V_yz的极值位置对应的是长方体边界的水平中心位置;V_zz的等值线图类似一系列的同心矩形,等值线在地下异常体密度变化边界分布密集,能够很好地确定密度变化,极大值的中心位置对应的是长方体的中心位置。

将单个长方体模型计算出来的重力梯度张量正演结果,利用正则化方法并结合深度加权函数对重力梯度张量各分量进行反演,其中初始参考模型m_ref=0,深度加权矩阵中的β取值为 3。各分量反演结果如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 单个长方体模型单分量反演结果

Fig.5 Inversion results of the single rectangular model

从图5可以看出,反演结果对异常顶部位置的分辨率比底部分辨率要高,这是由于位场本身的特征决定的。对比各个分量之间反演效果,各分量反演出来的剩余密度值与真实值比较接近,但是都出现了一定的负值,其中,V_xz、V_yy、V_yz反演出来的负值较大;各分量的反演结果在深度方向上延伸较大;V_zz反演出的剩余密度更接近真实值,反演的剩余密度极大值位置与真实位置非常吻合, V_xx、V_xy、V_xz、V_yy、V_yz、V_zz反演的密度值与理论模型密度的均方误差分别是0.214 8、0.205 3、0.201 5、0.217 2、0.213 1、0.192 7,说明了对于单分量的反演,基于非结构化网格的重力梯度张量反演方法是十分有效的,算法是可行的。

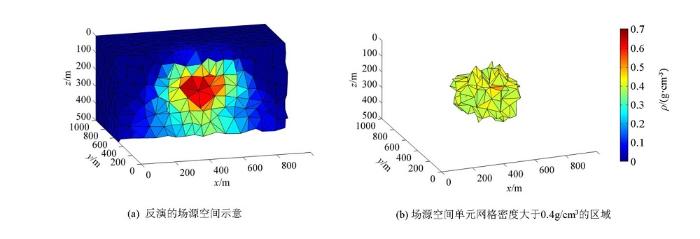
为了充分利用重力梯度张量各分量包含的密度、空间信息,对重力梯度张量的独立分量进行多分量的联合反演,结果如图6所示。对比图3与图6可知,多分量联合反演出来的密度值与理论模型的密度的均方误差为0.190 9,比任一单分量反演的均方误差都小,且利用多分量进行联合反演,其结果与理论模型极其吻合,这也证明了多分量联合反演的正确性。与单分量反演相比,联合反演出来的剩余密度值更加接近真实值,反演结果在水平方向和深度方向上都更加集中收敛于异常体的中心位置,利用多个独立分量进行联合反演能够更加准确反演出地下介质的剩余密度及埋藏位置,再次验证了算法的正确性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 单个长方体模型多分量联合反演结果

Fig.6 Multi-component joint inversion results of the single rectangular model

3 Y型岩脉模型

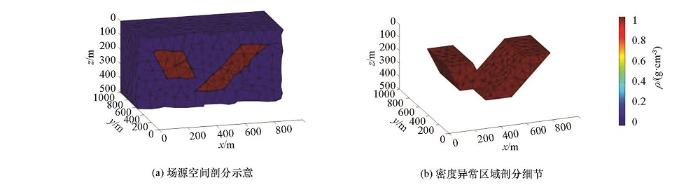
场源空间大小为1 000 m×1 000 m×500 m,如图7所示,场源空间存在一个Y型岩脉,其剩余密度都为1.0 g/cm³,左侧板状体顶部埋深为100 m,顶部中心在地表的投影位置为(200 m,500 m),顶部尺寸为200 m×400 m,底部埋深为300 m,底部中心在地表的投影位置为(300 m,500 m),顶部尺寸为200 m×400 m。右侧板状体顶部埋深为100 m,顶部中心在地表的投影位置为(700 m,500 m),顶部尺寸为200 m×400 m,底部埋深为400 m,底部中心在地表的投影位置为(500 m,500 m),顶部尺寸为200 m×400 m。x、y方向点距为50 m,测线长度为1 000 m。利用非结构化网格剖分软件将场源空间剖分,网格数目为9 408。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Y型岩脉模型非结构化网格剖分示意

Fig.7 The schematic diagram of a Y model using unstructured meshing

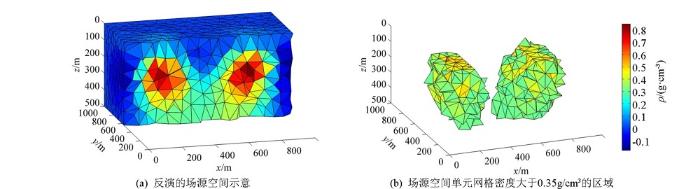
加入5%的高斯噪声后,利用重力梯度张量的5个相互独立分量进行多分量的联合反演,多分量联合反演的密度值与理论模型密度的均方误差为0.2347,反演结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Y型岩脉模型多分量联合反演结果

Fig.8 Multi-component joint inversion results of the Y model

对比图7与图8可知,利用多分量联合反演的结果与理论模型相似,反演的密度异常体能够很好地确定异常的位置、倾向。

4 结论

1)笔者利用吉洪诺夫正则化方法结合李耀国提出的广义目标函数将重力梯度张量各个分量正演结果分别进行了单分量反演;其次,为了充分利用重力梯度张量各分量数据使得反演结果更加准确,将5个相互独立的重力梯度张量分量进行了联合反演;最后,用长方体模型验证了算法的正确性,与长方体网格下的反演结果作对比说明非结构化网格下反演的优势,并通过Y型岩脉模型来说明方法的适应性。得出以下结论: 1) 对重力梯度张量各个分量的正演结果进行吉洪诺夫正则化反演,反演过程引入了深度加权函数,反演结果能够较好地确定地下异常体的水平、深度位置,反演剩余密度值也与理论值比较接近,验证了方法的正确性。

2) 与单分量的重力梯度张量反演相比,多分量的联合反演更加充分地利用了各个分量的信息,使得反演结果能够更加吻合初始模型。

3) 通过Y型模型说明了基于非结构化网格重力梯度张量反演算法具有较强的适应能力,能够较好地反演复杂模型。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王灿, 朱自强, 鲁光银 , 等.

重力梯度张量解析信号的正演模拟

[J]. 中国有色金属学报, 2013,23(9):2479-2497.