时移电阻率法归一化数据反演分辨电阻率结构微小变化

doi:10.11720/wtyht.2019.0008

时移电阻率法归一化数据反演分辨电阻率结构微小变化

马欢¹, 张洪洋², 郭越¹, 雷阳³, 谭捍东⁴, 吴萍萍¹, 张浩楠¹, 席彪¹

1. 防灾科技学院地球科学学院,河北廊坊 065201

2. 中海油田服务股份有限公司油田技术事业部资料解释中心,河北廊坊 065201

3. 核工业二〇三研究所地质勘查院,陕西咸阳 712000

4. 中国地质大学(北京) 地球物理与信息技术学院,北京 100083

The normalized data inversion of time-lapse resistivity method for resolving small resistivity changes

MA Huan¹, ZHANG Hong-Yang², GUO Yue¹, LEI Yang³, TAN Han-Dong⁴, WU Ping-Ping¹, ZHANG Hao-Nan¹, XI Biao¹

1. School of Earth Science, Institute of Disaster Prevention Science and Technology, Langfang 065201, China

2. Data Processing Interpretation Center of Well-Tech, China Oilfield Services Limited, Langfang 065201, China

3. Department of Geological Survey, No. 203 Research Institute of CNNC, Xianyang 712000, China

4. Geophysics and Information Technology Academy, China University of Geosciences, Beijing 100083, China

责任编辑: 沈效群

收稿日期: 2019-01-3 修回日期: 2019-06-12 网络出版日期: 2019-12-20

基金资助:

廊坊市科学技术研究自筹经费项目.  2018013099
中央高校基本科研业务费项目.  2018013099
国家自然科学基金项目.  41804119

Received: 2019-01-3 Revised: 2019-06-12 Online: 2019-12-20

作者简介 About authors

马欢(1988-),男,讲师,主要研究方向为地球物理电法数值模拟算法和应用。。

摘要

时移电阻率法能够应用于监测地下水污染物运移、衡量坡面稳定性等工程和环境问题。本文利用归一化时移电阻率法数据反演结果识别地下微小电阻率结构变化。首先,将初次采集数据作为背景数据,利用其归一化其他时刻时移电阻率法数据;再次,实现背景数据、时移数据以及归一化后时移数据的非线性共轭梯度反演。在合成数据算例中,保持观测系统不变,用相同反演参数和均匀半空间参考模型参与反演。反演结果表明,相对背景电阻率而言,归一化数据反演结果能够直接地、有效地分辨较为微小的电阻率结构动态变化,而传统电阻率反演不能分辨。

关键词： 时移 ; 电阻率法 ; 归一化 ; 反演 ; 分辨力

Abstract

The time-lapse resistivity method can be applied to engineering and environmental problems such as monitor groundwater contaminant transport, measure slope stability. In this paper, the normalized data inversion result of the time-lapse resistivity method was used to identify the subsurface structure of small resistivity changes. First, the data ratio normalization was adopted in which the initial data serve as the background data to normalize the data at other times. Next, the separate nonlinear conjugate gradients (NLCG) inversion result of initial data, time-lapse data and normalized time-lapse data were implemented. The same inverted parameters and homogenous half space model that was taken as the reference model were applied in all synthetic data examples. The inversion results show that the normalized data inversion results can effectively distinguish the small changes of resistivity relative to the background, but the conventional resistivity inversion almost cannot recognize it.

Keywords： time-lapse ; resistivity method ; normalization ; inversion ; differentiation

PDF (1450KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马欢, 张洪洋, 郭越, 雷阳, 谭捍东, 吴萍萍, 张浩楠, 席彪. 时移电阻率法归一化数据反演分辨电阻率结构微小变化. 物探与化探[J], 2019, 43(6): 1320-1325 doi:10.11720/wtyht.2019.0008

MA Huan, ZHANG Hong-Yang, GUO Yue, LEI Yang, TAN Han-Dong, WU Ping-Ping, ZHANG Hao-Nan, XI Biao. The normalized data inversion of time-lapse resistivity method for resolving small resistivity changes. Geophysical and Geochemical Exploration[J], 2019, 43(6): 1320-1325 doi:10.11720/wtyht.2019.0008

0 引言

时移电阻率法是一种时移地球物理方法,以常规电阻率法为基础,在同一位置不同时间,采用相同数据采集系统,观测与研究在不同时间建立的人工电流场分布规律,用于监测和理解地下电阻率结构动态过程,达到解决地表浅层监测问题的目的。相比常规电阻率法,时移电阻率法便于监测和了解地下的物理过程,不仅能够提供地下介质电阻率特性,而且还能监测电阻率结构的动态变化,主要应用于监测地下水溶质运移、浅地表松散沉积物的含水饱和程度以及探测基岩起伏特性等领域^[1]。从工程和环境角度来看,该方法可以监测含水构造的动态分布特征,服务于地质超前预报,还能探明地下水污染扩散和海水入侵^[2-5],衡量滑坡坡面稳定性^[6-7],探测大坝泄露问题和沼气污染地下水问题^[8],监测热液过程^[9]、地下水溶质运移^[10]以及估算非承压含水层的水文地质参数^[11]。可见,时移电阻率法在工程环境方面有较好的应用前景。

虽然时移电阻率法可以监测地下电阻率结构动态过程,但是有时地下结构的电阻率变化十分微小,使得发生电阻率变化的部分很难被发现。Daily 等将归一化后的时移电阻率数据资料代入反演算法中,以识别电阻率结构相对背景的变化情况^[12]。常用的归一化方法有两种:数据差和数据比^[12-13]。利用数据比归一化方法,使用初始时间观测数据归一化后续观测数据,再将归一化结果代入马奎特反演算法中,以突出电阻率结构发生变化的部分^[12,14,15]。随后,也有学者通过该归一化方法实现时移电阻率法反演算法,并应用时移电阻率法进行盐水示踪剂测试^[16]。但是在以上研究成果中参考模型都为均匀半空间。随着时移电阻率法反演算法的发展,学者们将观测数据与初始时间观测数据相减后的归一化数据体代入反演算法中(数据差归一化方法),并在此基础上考虑以初始时间数据的反演结果作为先验模型^[13,17,18]。总的来说,时移电阻率法和其反演算法研究表现为:国外研究多,国内研究少,而且针对微小电阻率结构变化的研究相对较少。所以,本文设计包含局部电阻率结构的微小变化的理论模型,采用数据比归一化处理手段,以均匀半空间作为参考模型,将归一化后的时移电阻率数据资料带入共轭梯度反演算法中,将时移数据反演结果与常规电阻率反演结果对比,讨论电阻率结构相对背景的变化情况。

1 原理方法

1.1 正演原理

与常规电阻率法相比,时移电阻率法的基本方程同样满足泊松方程,但是方程中的参数都是随时间变化的。那么,实现时移电阻率法正演算法只需建立多组表征电阻率动态的地电模型,进行多次常规电阻率法正演模拟即可,基本方程如下:

(1)

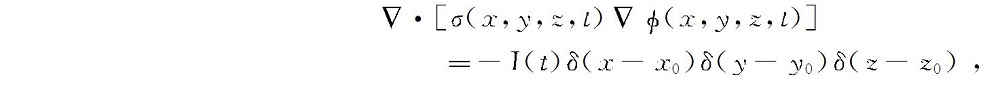
其中:σ为随时间变化的地下介质电导率(S/m);ϕ为随时间变化的电位(V);(x₀,y₀,z₀)为点电源坐标;I为供电时刻的电流强度(A/m³);δ(·)为狄拉克函数。随后,采用有限差分法将泊松方程(1)和其边界条件(第二类和第三类边界条件)进行离散,形成大型线性方程组,使用不完全LU分解的稳定双共轭梯度法(BICGSTAB)求解线性方程组,获得不同时刻不同电阻率分布的电位,进一步求得其视电阻率ρ_s。

1.2 归一化方法

归一化处理能够减小随机噪声和仪器设备背景噪声引起的反演误差。常见的归一化方法有两种:数据比、数据差。这两种方法都是利用最初时刻采集的数据归一化其他时刻采集的数据。假设,视电阻率数据ρ_s由9个时刻所采集的数据构成,即ρ_s=[ρ_s0,ρ_s1,…,ρ_s9]。那么,数据比和数据差归一化公式如下^[13,15]:

(2)

ρ_{s n, i} = \{\begin{array}{l} \frac{ρ_{s i}}{ρ_{s 1}} ρ_{sh} \\ ρ_{s i} - ρ_{s 1} \end{array}, i = 1,2, \dots, 9

其中:ρ_sh是电阻率模型为均匀半空间的观测数据向量,ρ_s_i是时移视电阻率数据,ρ_s1是背景数据。本文归一化方法使用数据比归一化,该方法允许跟踪相对于背景值的50%或更小的电阻率的时间变化。

1.3 共轭梯度反演

本文反演算法采用共轭梯度算法^[19],将归一化后的数据ρ_s_n_,_i代入共轭梯度反演中。定义目标函数为:

(3)

\begin{array}{l} ϕ = (d_{obs} {- d)}^{T} C_{d}^{- 1} (d_{obs} - d) + \\ λ (m - m_{ref})^{T} L^{T} L (m - m_{ref}) 。 \end{array}

其中:d_obs是观测视电阻率向量;d是正演视电阻率向量;C_d 是随机误差矩阵;λ是拉格朗日乘子,在反演迭代过程中用于平衡数据误差和模型正则化的影响;m_ref是电导率先验模型向量;m是每次迭代所更新的电导率模型向量,在算法中取模型向量的自然对数ln(σ),即电导率的自然对数;L是拉普拉算子,对空间X、Y、Z三个方向的二阶偏导数;上标T表示矩阵的转置。

2 正演算法有效性验证

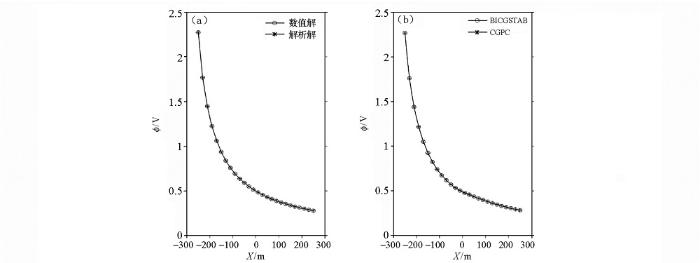
由于上述原理方法中介绍的时移电阻率法正演是将多个时刻的地电模型分别进行正演,与常规电阻率法的正演算法本质上相同,因此,这里仅对常规电阻率法地电模型的正演模拟结果进行验证即可。首先,设定图1中的观测系统,实心圆点为场源,倒三角为接收点。对比电阻率为1 000 Ω·m的均匀半空间解析解和数值解(图2a),拟合程度较好,相对误差为4.38×10^-5。其次,在电阻率为100 Ω·m的均匀半空间中放置一个几何尺寸为100 m×100 m×70 m,埋深为70 m,电阻率为10 Ω·m的棱柱体(图1),将其数值模拟结果与Spitze的CGPC数值模拟^[20]结果对比(图2b),拟合程度较好,相对误差为4.88×10^-4。从两个验证结果可以看出,本文的数值模拟算法是有效的。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 理论模型及观测系统示意

Fig.1 Theorical model and observation system

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 正演结果对比

a—与解析解对比结果; b—与CGPC对比结果

Fig.2 The comparison of forward results

a—the numerical solutions (BICGSTAB) compared with analytical solutions; b—the numerical solutions (BICGSTAB) compared with CGPC solutions

3 算例

本文设定三维观测系统采集数据,如图3所示,将供电电极依次单电极供电,观测各个“圆圈”表示的测点的电位(二极装置)。随后,通过设计两个不同二维理论模型,模拟两个时刻的地下电阻率结构(图4)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 观测系统

Fig.3 Observation system

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 理论模型

Fig.4 Theorical model

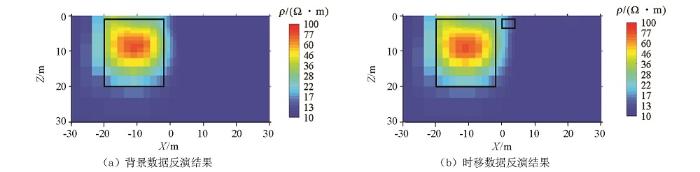
在10 Ω·m的均匀半空间设置一个埋深为 1 m,电阻率为100 Ω·m的高阻体,几何尺寸为18 m×19 m。为了体现相对背景的微小变化,在第一组模型的基础上,与高阻体的水平距离仅为2 m处设置一个埋深为1 m,几何尺寸相对较小(4 m×2.6 m),电阻率为35 Ω·m的棱柱体。

两套数据的正反演网格大小均为45×33×31,场源和观测点位置及排列均保持不变(见图3),拉格朗日乘子均为10^-6,合成数据均添加5%的随机高斯误差。

首先,以10 Ω·m的均匀半空间作为参考模型单独反演上述两组模型。反演结果可以看出,第一组和第二组模型的高阻体结果十分清晰(图5),而第二组模型的小棱柱体并不明显(图5b)。为了量化两组模型单独反演结果的差异,探究其差异能否发现小棱柱体,计算两者相对变化量(图5b结果减去图5a结果)。如图6所示,小规模棱柱体位置处的相对变化量表现为最大值,貌似从色彩上可以确定小棱柱体的存在,但是从数量级上来看,整个电阻率模型空间的相对变化量最大值为0.17 Ω·m,显得十分微弱,几乎没有变化。所以根本无法从数量级上说明存在电阻率结构变化,分辨率差。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 常规电阻率反演结果

Fig.5 Conventional resistivity inversion results

图6

新窗口打开| 下载原图ZIP| 生成PPT

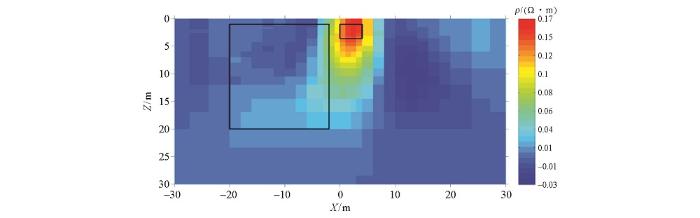
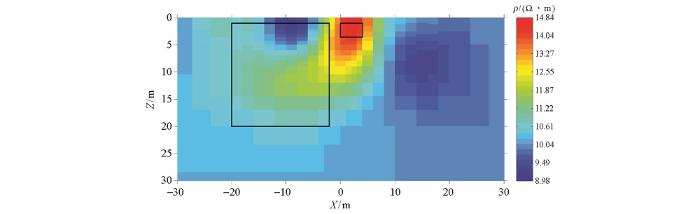
图6 时移数据反演结果相对背景数据反演结果变化量

Fig.6 Time-lapse data inversion result minus background data inversion result

于是,通过式(2)的数据比归一化方法(ρ_sh=10 Ω·m),将第一组理论模型的合成数据作为背景数据归一化第二组模型的合成数据,还是以10 Ω·m的均匀半空间作为参考模型,将归一化后的数据代入反演,得到图7。从反演结果中看出,相对背景反演结果的变化情况。虽然图7中有很多地方都存在相对变化,但是结果中最大值的位置和其数量级可以反映出小规模棱柱体所在。因此,从以上结果中可知:相对背景电阻率结构而言,归一化时移数据的反演结果能够直接反映出电阻率结构发生微小变化的位置,而常规电阻率反演则不能反映出电阻率结构的微小变化。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 归一化时移数据反演结果

Fig.7 Inversion result of normalized time-lapse data

4 结论

时移电阻率法不仅能够像常规电阻率法那样恢复地下电阻率结构,而且还便于监测和了解地下的物理过程。本文使用数据比归一化方法处理时移电阻率法数据,再利用共轭梯度反演算法反演归一化后的数据。本文合成数据算例表明:当地下局部电阻率结构相对背景电阻率存在微弱的变化时,常规电阻率法反演分辨力弱,很难识别局部电阻率结构微小变化的位置,而归一化时移电阻率法数据的反演结果能够直接分辨局部电阻率结构随时间的微小变化。但是,当数据采集环境存在强干扰时,现有常规电阻率法仪器的分辨率和稳定性不能保证微小变化引起视电阻率异常的准确性。然而,伪随机信号电法仪(KGR和ABOLLO)能够弥补这方面缺陷(能在干扰环境下,完成高精度视电阻率测量),为实现时移电阻率法数据观测提供有利条件。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Loke M

, Dahlin

, Rucker D

Smoothness-constrained time-lapse inversion of data from 3D resistivity surveys

[J]. Near Surface Geophysics, 2014,12(1):5-24.