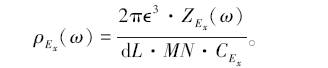0 引言
可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] 。在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] 。如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] 。
在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量。航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] 。多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率。采用2n [15 ,16 ,17 ] 。
不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同。可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] 。广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] 。李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] 。佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] 。
鉴于水平电偶极源在可控源电磁系统中的广泛应用,测量垂直磁场在时间域电磁系统应用研究较多,而在频率域应用研究较少。本文通过计算水平电偶极源激发,水平层状地质模型水平电场Ex 分量和垂直磁场Hz 分量频率域全区视电阻率,考查了不同收发距条件下各场分量对层状模型的响应能力。并与层状模型大地电磁测深(MT)卡尼亚电阻率和可控源音频大地电磁测深(CSAMT)卡尼亚电阻率进行比较,研究了不同收发距Hz 分量全区视电阻率对大埋深高、低阻薄层的探测能力,对可控源电磁测深中收发距选择、场分量选择,工作频率范围选择等给出工作建议。
1 方法原理
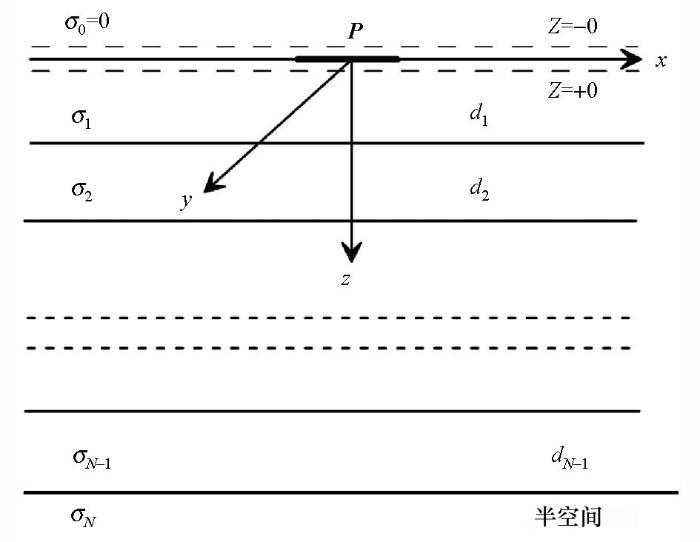
水平接地双极源层状计算模型如图1 所示。N 层水平层状介质中第n 层的电导率和层厚度分别记为σn 和dn ,假设各层不含铁磁性物质。水平电偶极子(接地双极源)位于层状介质表面,偶极矩为P =I dL (I 为谐变电流I =I 0 e-i wt x 轴指向偶极矩方向(即y =0的方向),z 轴垂直向下,求层状介质表面的电磁场分布。
图1
图1
水平电偶极源层状地电模型
Fig.1
Layered geoelectricity model with horizontal electric dipole source
略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为:
(1a) E r = I d L 2 π cos ϕ i ωμ r ∫ 0 ∞ 1 λ + m 1 R * J 1 ( λr ) d λ - ρ 1 ∫ 0 ∞ λ m 1 R J 0 ( λr ) d λ + ρ 1 r ∫ 0 ∞ m 1 R J 1 ( λr ) d λ ,
(1b) E ϕ = I d L 2 π sin ϕ ρ 1 r ∫ 0 ∞ m 1 R J 1 ( λr ) d λ - i ωμ ∫ 0 ∞ λ λ + m 1 R * J 0 ( λr ) d λ + i ωμ r ∫ 0 ∞ 1 λ + m 1 R * J 1 ( λr ) d λ ,
(1c) H r = - I d L 2 π r sin ϕ ∫ 0 ∞ λ λ + m 1 R * J 1 ( λr ) d λ + r ∫ 0 ∞ m 1 R * λ λ + m 1 R * J 0 ( λr ) d λ ,
(1d) H ϕ = I d L 2 π r cos ϕ ∫ 0 ∞ λ λ + m 1 R * J 1 ( λr ) d λ ,
(1e) H z = I d L 2 π sin ϕ ∫ 0 ∞ λ 2 λ + m 1 R * J 1 ( λr ) d λ 。
R * = coth m 1 d 1 + cot h - 1 m 1 m 2 coth m 2 d 2 + L + cot h - 1 m N - 1 m N ; R = coth m 1 d 1 + cot h - 1 m 1 m 2 ρ 1 ρ 2 coth m 2 d 2 + L + cot h - 1 m N - 1 m N ρ N - 1 ρ N ;
mj = λ 2 - k j 2 k j 2 ωμ 0 σn ,μ 0 为自由空间导磁率;λ 称为空间频率,它具有距离倒数的量纲。
特别地,当N =1时,可得到均匀半空间表面电磁场各分量的表达式:
(2a) E r 0 = I d L 2 π σ r 3 cos ϕ [ 1 + e i kr ( 1 - i kr ) ] ,
(2b) E ϕ 0 = I d L 2 π σ r 3 sin ϕ [ 2 - e i kr ( 1 - i kr ) ] ,
(2c) H r 0 = - 3 I d L 2 π r 2 sin ϕ I 1 i kr 2 K 1 i kr 2 + i kr 6 I 1 i kr 2 K 0 i kr 2 - I 0 i kr 2 K 1 i kr 2 ,
(2d) H ϕ 0 = I d L 2 π r 2 cos ϕ I 1 i kr 2 K 1 i kr 2 ,
(2e) H z 0 = - 3 I d L 2 π k 2 r 4 sin ϕ 1 - e i kr 1 - i kr - 1 3 k 2 r 2 。
以上各式中,μ 0 为自由空间的导磁率。ω 为谐变电流的圆频率。I 0 i kr 2 I 1 i kr 2 K 0 i kr 2 K 1 i kr 2 i kr 2 k 为波数。
1.1 电磁场计算方法
令:水平电偶极矩PE = I d L 2 π
(3a) E r = ( P E / r ) cos ϕ [ i ωμ I 4 - r ρ 1 I 5 + ρ 1 I 6 ] + E r 0 ,
(3b) E ϕ = ( P E / r ) sin ϕ [ i ωμ I 4 - i ωμr I 7 + ρ 1 I 6 ] + E ϕ 0 ,
(3c) H r = ( - P E / r ) sin ϕ ( I 1 + 0.5 I 9 + r ( I 2 + 0.5 I 10 ) )
(3d) H ϕ = P E cos ϕ r ( I 1 + 0.5 I 9 ) ,
(4a) I 1 = ∫ 0 ∞ λ λ + m 1 R * - 0.5 J 1 λr d λ ,
(4b) I 2 = ∫ 0 ∞ m 1 R * 1 λ + m 1 R * - 0.5 λ J 0 λr d λ ,
(4c) I 3 = ∫ 0 ∞ λ λ + m 1 / R * - 0.5 λ J 1 ( λr ) d λ ,
(4d) I 4 = ∫ 0 ∞ λ λ + m 1 / R * - 1 λ + m 1 J 1 ( λr ) d λ ,
(4e) I 5 = ∫ 0 ∞ λ m 1 1 R - 1 J 0 ( λr ) d λ ,
(4g) I 7 = ∫ 0 ∞ 1 λ + m 1 / R * - 1 λ + m 1 λ J 0 ( λr ) d λ ,
(4k) E r 0 = P E r 3 ρ cos ϕ [ 1 + e i kr ( 1 - i kr ) ] ,
(4l) E ϕ 0 = P E r 3 ρ sin ϕ [ 2 - e i kr ( 1 - i kr ) ] 。
在计算层状介质表面的电场分量和磁场垂直分量时,减去了均匀半空间的场,这是为了保证在λ →∞时积分核快速趋于零,从而保证积分收敛,也节省计算时间。
这三个极限的收敛速度是很快的。据此,将式(1)各式改写为式(3)。
层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] 。但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度。本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] 。
文献[20 ]中,Chave提出了汉克尔变换的数值积分算法。Chave算法的基本思路是,采用高斯求积方法对有限区间积分进行计算,进而结合连分式展开方法加快部分积分和的收敛速度。一反数字滤波法的常规做法,Chave算法使用期望误差(绝对误差/相对误差)来控制计算是继续或是终止。为了直接采用数值求积方法计算式(4),可将积分写成如下部分积分之和:
(8) f ≈ S = ∑ n = 0 N P n ,
(9) P n = ∫ Z n Z n + 1 K ( λ , P ) J i ( λr ) d λ 。
式中:Ji (λr )为第1类的i 阶Bessel函数;Zn 为 Ji (λr )的第n 个零点用距离r 归一化后的值;N 为参与求和的部分积分项的个数,取决于计算方法;Pn 可采用Gauss求积公式计算
(10) P n ≈ ∑ j = 1 M h j K ( a j , P ) J i ( a j r ) 。
式(10)中M 是求积节点个数,aj 为求积节点,hj 为求积系数。
(11) S = d 0 1 + d 1 1 + d 2 1 + d 3 1 + … d n ,
式中d 0 ,d 1 ,d 2 ,…,dN 可由区间积分项Pn 求得。
本文采用文献[21 ]介绍的数值积分方法,在matlab计算平台中,预先计算了贝赛尔函数Ji (λr ),i =0,1的300个零点,最初的几个零点之间的区间积分采用matlab 的自适应Simpsons积分函数(QUAD),之后的积分区间根据计算精度,采用自适应Lobatto积分函数(QUADL),积分项的求和采用Euler法加速其收敛,积分的终止条件是最后加入的区间积分项小于设定的容许误差,或者已计算了设定的所有区间数。实际上计算不超过30个过零点区间就可达到所需要的精度。
由上,可计算出水平电偶极源层状模型电场和磁场各分量频率响应。
1.2 全区视电阻率计算方法
由计算出的水平电偶极源层状模型的各场分量的频率响应,汤井田给出了各场分量全区视电阻率定义[14 ] 。本文主要以水平电场Ex 和垂直磁场Hz 分量计算全区视电阻率。为方便论述,此处重写出均匀半空间表面水平电偶源产生的电磁场:
12a E x = 2 I d L 2 π r 3 ρ [ 3 cos ϕ - 2 + e i kr ( 1 - i kr ) ]
(12b) H y = - I d L 4 π r 2 [ si n 2 ϕ ( 6 I 1 K 1 + i kr ( I 1 K 1 - I 0 K 1 ) ) - 2 co s 2 ϕ I 1 K 1 ] ,
(12c) H z = - I d Lρ 2 π r 4 μω sin ϕ [ 3 - e i kr ( 3 - 3 i kr - k 2 r 2 ) ] 。
式中:Ex 、Hy 和Hz 分别为电场和磁场的水平分量和垂直分量,r 为接收点到偶极中心矢径的模,φ 为r 和x 轴的夹角。I 是电流强度,dL 是偶极子长度。ρ 和μ 是均匀半空间的电阻率和导磁率,ω 为角频率,k 为电磁波的波数,k 2 =iωμ/ρ ,i= - 1 I 0 和K 1 、K 0 分别是第一和第二类以ikr/ 2为宗量的虚宗量贝塞尔函数,0和1表示阶数。
(13a) C E = 3 co s 2 ϕ - 2 + e i kr ( 1 - i kr ) ,
(13b) C H = [ si n 2 ϕ ( 6 I 1 K 1 + i kr ( I 1 K 0 - I 0 K 1 ) ) - 2 co s 2 ϕ I 1 K 1 ] kr ,
(13c) C Z = 3 - e i kr ( 3 - 3 i kr - k 2 r 2 ) ;
(14b) H z = - I d Lρ 2 π r 4 μω sin ϕ · C Z 。
(15b) Φ e | E x | = arctan Im ( E x / C E ) Re ( E x / C E ) ;
(16a) ρ e | H z | = 2 π r 2 I d L sin ϕ μω H z C Z ( φ ≠ 0 0 ) ,
(16b) Φ e | H z | = arctan Im ( H z / C Z ) Re ( H z / C Z ) 。
本文给出采用循环互相关算法计算全区视电阻率的方法[18 ] 。观测中需要同时记录发送电流和电场或磁场时间序列。当观测场值是水平电场Ex 分量时间序列时,观测值是接收电极间的电位差时间序列, V E x Ex ·MN ,MN 为接收电场的电极间距,采用循环互相关算法可估计出阻抗谱:
(17) Z E x ( ω ) = P C V E x s ( ω ) P C I AB s ( ω ) ,
式中: P C V E x s ( ω )为参考信号SS与接收电位差信号 V E x P C I AB s ( ω )为参考信号SS 与水平电偶源AB 发射电流信号IAB (t )的互功率谱。
由均匀大地表面水平电偶极子源产生的电场Ex 计算公式:
(18) E x = ρI d L 2 π r 3 [ ( 1 - 3 si n 2 ( φ ) ) + ( 1 - i k 1 r ) exp ( i k 1 r ) ] 。
式中:ρ 为均匀大地的电阻率,I 是发射电流,r 是接收电极MN 中点至发射偶极AB 中点的距离,φ 是接收电极MN 中点至发射AB 极中点连线与AB 极连线的夹角。dL 是发射AB 极间距。 k 1 2 ωμ 0 /ρ 为均匀大地的波数。
式(18)两边除以电流I 与式(17)对应相等,可得:
(19) Z E x ( ω ) = ρ ( ω ) d L · MN 2 π r 3 C E x , ( 19 )
(20) C E x = ( 1 - 3 si n 2 ( φ ) ) + ( 1 - i k 1 r ) exp ( i k 1 r ) 。
Z E x ( ω )就是由观测电场Ex 电位差值和激发电流I 循环互相关辨识得到的大地的阻抗。由此可得大地的全区视电阻率谱:
(21)
式中: C E x
当观测电磁场值是垂直磁场Hz 分量时间序列时,由发送电流时间序列和垂直磁场时间序列,采用循环互相关算法可估计出阻抗谱:
(22) Z H z ( ω ) = P C H z s ( ω ) P C I AB s ( ω ) ,
式中: P C H z s ( ω )为参考信号SS 与接收垂直磁场信号Hz 的互功率谱, P C I AB s ( ω )为参考信号SS 与水平电偶极子源AB 发射电流信号IAB (t )的互功率谱。
由均匀大地表面水平电偶极子源产生的垂直磁场Hz 计算公式为:
(23) H Z = - 3 I d L 2 π k 1 2 r 4 sin φ 1 - 1 - i k 1 r - 1 3 ( k 1 r ) 2 exp ( i k 1 r ) ,
式中:I 是发射电流,r 是磁场接收点P 至发射极AB 中点的距离,φ 是磁场接收点P 至发射极AB 中点连线与AB 极延长线的夹角,dL 是发射极AB 长度, k 1 2 ωμ 0 /ρ 为均匀大地的波数,μ 0 是磁导率。
式(23)两边除以电流I 与式(22)对应相等,可得:
(24) Z H z ( ω ) = - 3 d L · ρ ( ω ) i ω μ 0 2 π r 4 sin φ C H z
(25) C H z = 1 - 1 - i k 1 r - 1 3 ( k 1 r ) 2 exp ( i k 1 r ) 。
Z H z ( ω )就是由观测垂直磁场Hz 和发送电流I 循环互相关辨识得到的大地的频率域响应。由此可得大地的全区视电阻率谱:
(26) ρ H z ( ω ) = 2 π ω μ 0 r 4 · Z H z ( ω ) 3 i · d L · sin φ · C H z 。
式中 C H z
对于激发极化效应的模拟计算,采用在频率域Cole-Cole模型来描述:
(27) ρ ( ω ) = ρ 0 1 - m 1 - 1 1 + ( i ωτ ) c ,
式中:ρ 0 为直流电阻率,m 为极化率,ω 为角频率,τ 为时间常数,c 为频率系数。
式(21)和式(26)右端均隐含有视电阻率,需要采用迭代算法求解。全区视电阻率迭代计算过程如下:
1) 给出全区视电阻率初值ρ (0) 。此初值是任意的,可选取为相应的波区视电阻率;
2) 将ρ (0) 代入式(21)和式(26),并进而求得第一次迭代视电阻率值ρ (1) ;
(28) | ρ ( 1 ) - ρ ( 0 ) | ρ ( 0 ) ≤ ε ;
式中ε 为给定的正的小数。若式(28)成立,计算相应的相位值,并停止迭代。若式(28)不成立,令ρ (0) =ρ (1) ,返回步骤(2),直到式(28)成立。
2 模型计算
2.1 模型一——D型
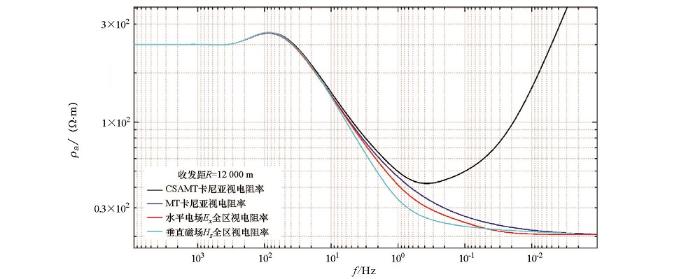
地电模型参数如表1 所示。计算参数:供电电流I =40 A,电偶极子长度dL =1 800 m,收发距R =12 000 m,赤道偶极测量装置。计算了水平电场Ex 全区视电阻率、垂直磁场Hz 全区视电阻率,同时与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率进行比较。从图2 的频谱曲线可以看出,大于1 000 Hz高频段全区视电阻率反映出第一层电阻率300 Ω·m,低于0.01 Hz低频段Ex 全区视电阻率和垂直磁场Hz 全区视电阻率,与MT卡尼亚视电阻率趋势一致,趋于第二层视电阻率20 Ω·m。而CSAMT卡尼亚视电阻率在低于1 Hz低频段不能正确反映地层特征。
图2
图2
水平电偶源D型地电模型全区视电阻率频谱
Fig.2
whole zone apparent resistivity spectrum of D-type geoelectricity model with horizontal electric dipole Source
2.2 模型二——G型
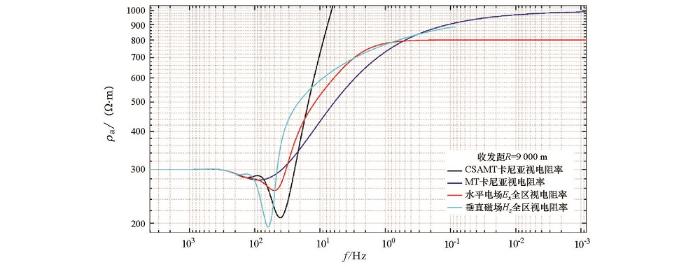
计算参数:供电电流I =40 A,电偶极子长度dL =1 800 m,收发距R =9 000 m,赤道偶极测量装置。计算了水平电场Ex 全区视电阻率、垂直磁场Hz 全区视电阻率,同时与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率进行比较。从图3 的频谱曲线可以看出,大于1 000 Hz高频段全区视电阻率反映出第一层电阻率300 Ω·m,低于1 Hz低频段Ex 全区视电阻率和垂直磁场Hz 全区视电阻率,与MT卡尼亚视电阻率趋势一致,趋于第二层视电阻率1 000 Ω·m。Ex 全区视电阻率在低于0.4 Hz频段变得平直,不再趋于第二层电阻率真值,是由于电场已进入近区,不再反映地电信息;而Hz 全区视电阻率在低于0.1 Hz频段还有逼近第二层电阻率真值的趋势。但同样受近区影响,垂直磁场全区视电阻率只响应到0.085 Hz左右,低于这个频率不再反映地电信息;同时也说明垂直磁场进行近区的频率低于水平电场进行近区的频率。而CSAMT卡尼亚视电阻率在低于10 Hz低频段就不能正确反映地层特征。
图3
图3
水平电偶源G型地电模型全区视电阻率频谱
Fig.3
whole zone apparent resistivity spectrum of G-type geoelectricity model with horizontal electric dipole Source
2.3 模型三——H型
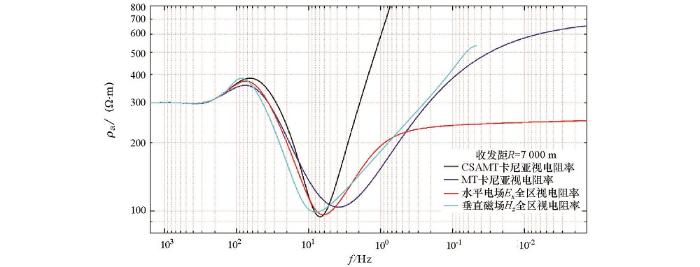
计算参数:供电电流I =30 A,电偶极子长度dL =1 800 m,收发距R =7 000 m,赤道偶极测量装置。第二层含有激电信息:m =0.35,τ =0.12 s, c =0.25。计算了水平电场Ex 全区视电阻率、垂直磁场Hz 全区视电阻率,同时与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率进行比较。从图4 水平电偶源H型型地电模型全区视电阻率频谱曲线可以看出,大于1 000 Hz高频段Ex 和Hz 全区视电阻率反映出第一层电阻率300 Ω·m,低于1 Hz低频段Ex 全区视电阻率和垂直磁场Hz 全区视电阻率,与MT卡尼亚视电阻率趋势一致,趋于第三层视电阻率700 Ω·m。Ex 全区视电阻率在低于0.1 Hz频段变得平直,受近区影响不再趋于第三层电阻率真值,而垂直磁场Hz 全区视电阻率在低于0.1 Hz频段,响应至0.05 Hz,还有逼近第三层电阻率真值的趋势,低于0.05 Hz不再反映地电信息,低于水平电场进入近区的频率。而CSAMT卡尼亚视电阻率在低于5 Hz低频段就不能正确反映地层特征。
图4
图4
水平电偶源H型地电模型全区视电阻率频谱
Fig.4
whole zone apparent resistivity spectrum of H-type geoelectricity model with horizontal electric dipole Source
2.4 模型四——K型
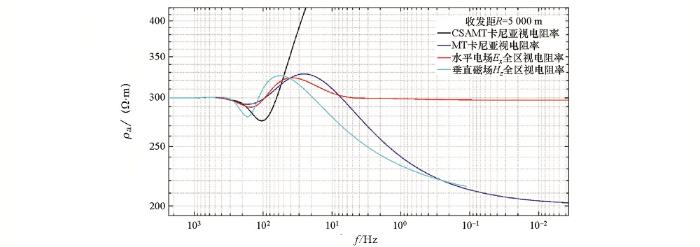
地电模型参数如表4 所示。计算参数:供电电流I =30 A,电偶极子长度dL =1 800 m,收发距R =5 000 m,赤道偶极测量装置。计算了水平电场Ex 全区视电阻率、垂直磁场Hz 全区视电阻率,同时与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率进行比较。从图5 水平电偶源K型地电模型全区视电阻率频谱曲线可以看出,大于800 Hz高频段Ex 和Hz 全区视电阻率反映出第一层电阻率300 Ω·m,Ex 全区视电阻率在低于1 Hz频段变得平直,说明电场已进入近区,不再趋于第三层电阻率真值。低于1 Hz低频段Hz 全区视电阻率与MT卡尼亚视电阻率趋势一致,还有逼近第三层电阻率真值200Ω·m的趋势,但同样受近区影响,只响应到0.1 Hz,之后不再反映地电信息。小收发距条件下,垂直磁场进入近区的频率低于水平电场进入近区的频率。而CSAMT卡尼亚视电阻率在低于100 Hz低频段就不能正确反映地层特征。原因是近区Hy 场值太小;同时也说明,垂直磁场Hz 全区视电阻率,在较小收发距条件下,就能有大探测深度的能力。
图5
图5
水平电偶源K型地电模型全区视电阻率频谱
Fig.5
whole zone apparent resistivity spectrum of K-type geoelectricity model with horizontal electric dipole Source
2.5 模型五——KH型
计算参数:供电电流I =30 A,电偶极子长度dL =1 800 m,收发距R 分别为7 000、12 000、25 000 m,赤道偶极测量装置。第三层含有激电信息:m =0.35, τ =0.1 s, c =0.25。计算了水平电场Ex 全区视电阻率、垂直磁场Hz 全区视电阻率,同时与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率进行比较。
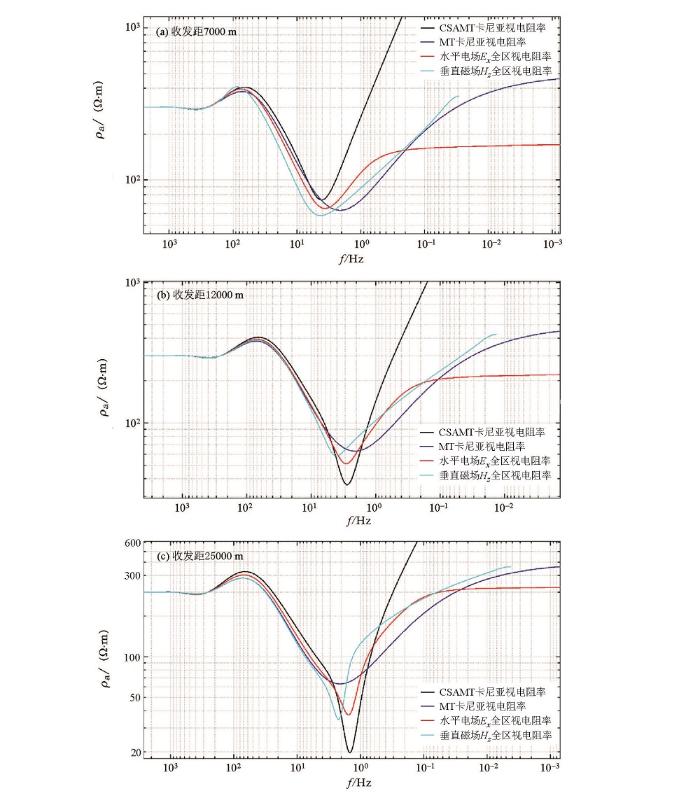
从图6 水平电偶源KH型地电模型全区视电阻率频谱曲线可以看出,大于1 000 Hz高频段Ex 和Hz 全区视电阻率与MT卡尼亚视电阻率和CSAMT卡尼亚视电阻率一样,反映出第一层电阻率300 Ω·m,Ex 全区视电阻率在低于0.1 Hz频段变得平直,说明已进入近区,不再趋于第三层电阻率真值。由图6 c和图6 a比较可知,随收发距增大,Ex 全区视电阻率也增大,收发距在7 000 m时,0.01 Hz全区视电阻率为166.95 Ω·m;收发距在12 000 m时,0.01 Hz全区视电阻率为216.69 Ω·m;收发距在25 000 m时,0.01 Hz全区视电阻率为320.5 Ω·m;但不能反映地层电阻率真值,进入近区的频率变低。;
图6
图6
水平电偶源KH型地电模型不同收发距全区视电阻率频谱
Fig.6
whole zone apparent resistivity spectrum of KH-type geoelectricity model with horizontal electric dipole source with different transmit-receive distance
Hz 全区视电阻率在低于4 Hz低频段与MT卡尼亚视电阻率趋势一致,还有逼近第四层电阻率真值500 Ω·m的趋势,收发距在7 000 m时,只响应到0.03 Hz,低于这个频率进入近区,不再反映地电信息;增大收发距,进入近区的频率变低。随收发距增大,收发距在12 000 m时,低于0.015 Hz进入近区;收发距在25 000 m时,低于0.0045 Hz进入近区。在不同收发距条件下,Hz 全区视电阻率进入近区的频率均低于Ex 全区视电阻率进入近区的频率。说明Hz 全区视电阻率在小收发距条件下更有利于穿透中间层揭示出基底层。而同样受近区影响,CSAMT卡尼亚视电阻率在低于1 Hz低频段就不能正确反映地层特征。
3 结论
通过计算水平电偶源层状介质的电磁场响应,并反算出视电阻率。结果表明,正演计算层状介质的电磁场响应及全区视电阻率结果是正确的,计算程序是可靠的。
计算表明,水平电偶极源电磁场在不同收发距条件下进入近区的频率不同。收发距越大,磁场和水平电场进入近区的频率越低。在近区,水平电场全区视电阻率不随频率变化了,不能进行频率测深;垂直磁场也有最低响应频率,低于这个频率,不能反映地电信息。在相同收发距条件下,垂直磁场Hz 进入近区的频率低于水平电场Ex 进入近区的频率近一个数量级。
Ex 和Hz 全区视电阻率以及可控源卡尼亚视电阻率与层状模型大地电磁测深(MT)卡尼亚视电阻率在高频段(>1 000 Hz)一致性较好,而在低频段(<100 Hz)分异较大。收发距越大,相应频率越低。这说明水平电偶极源在高频段、大收发距条件下满足远区条件,类似平面波了;而在低频段、小收发距条件下,受地层电阻率、偶极源长度、收发距等因素影响,电磁场不再满足平面波场条件了。可控源(CSAMT)卡尼亚视电阻率定义进入近区最早,对深层响应能力最低。Ex 全区视电阻率在低频段变得平直,也是因为近区影响所致;Hz 低于最低响应频率的全区视电阻率也不反映地电信息了,说明已进入近区。
水平电偶极源赤道偶极装置Ex 和Hz 全区视电阻率均能反映出地层电性特征变化,在大收发距条件下,对高、低中间薄层均能有较好的分辨。在较小收发距条件下,Hz 全区视电阻率较Ex 全区视电阻率更利于接近深部电阻率真值。对于水平电偶源频率电磁测深,对于大埋深目标体勘查,磁场传感器应具有宽的频率响应,理想的频率响应范围是104 ~10-3 Hz。
根据计算结果,在接收条件允许的条件下,大收发距Hz 全区视电阻率和Ex 全区视电阻率对地层分辨能力好于小收发距。多收发距观测有利于提高对地层的辨识。
参考文献
View Option
[1]
Kaufman A A Alekseev D Oristaglio M . Principles of electromagnetic methods in surface geophysics
[M]. Elsevier , 2014 .
[本文引用: 3]
[2]
Zhdanov M S . Foundations of geophysical electromagnetic theory and methods
[M]. Elsevier , 2017 .
[本文引用: 2]
[3]
Chave A D Jones A G The magnetotelluric method: theory and practice
[M]. Cambridge University Press , 2012 .
[4]
Viacheslav V . Spichak. Electromagnetic sounding of the Earth’s interior: theory, modeling, practice(2nd ed)
[M]. Elsevier , 2015 .
[本文引用: 1]
[5]
殷长春 . 航空电磁理论与勘查技术 [M]. 北京 : 科学出版社 , 2018 .
[本文引用: 3]
Yin C C Aeromagnetic theory and exploration technology [M]. Beijing : Science Press , 2018 .
[本文引用: 3]
[6]
周海根 , 多场源地空频率域电磁探测方法研究
[D]. 长春:吉林大学 , 2017 .
[本文引用: 2]
Zhou H G . Research on ground-airborne frequency-domain electromagnetic methods with multiple sources
[D]. Changchun: Jilin University , 2018 .
[本文引用: 2]
[7]
Richard A Geyer . Handbook of geophysical exploration at sea(2nd ed)
[M]. CRC Press , 2018 .
[本文引用: 3]
[8]
王若 , 殷长春 , 王妙月 , 等 . CSAMT法一维层状介质灵敏度分析
[J]. 地球物理学进展 , 2014 ,29 (3 ):1284 -1291 ,doi: 10.6038/pg20140339 .
Magsci
[本文引用: 1]
<p>为改善CSAMT一维反演的实用性,本文以电磁场数值模拟为基础,推导出偶极源激发下频率域电磁反演中的偏导数公式.并以三层水平层状地电模型为例,针对同线装置和赤道装置两种形式,利用扰动法对本文的半解析算法结果进行验证.对比结果表明无论同线还是赤道装置,本文半解析结果和扰动法计算结果拟合程度非常好,验证了偏导数公式推导及程序代码的正确性.进而,分析了CSAMT观测数据对中间薄层参数的灵敏度.灵敏度特征分析表明:CSAMT观测资料对中间低阻薄层比较敏感,对高阻薄层的分辨率较低,但对层厚度,即便是高阻薄层,仍存在较高的灵敏度.频率对层参数的灵敏度有重要影响.实际应用中,应同时考虑资料和参数加权,以提高中间层参数的求解能力.本文的算法不仅有助于CSAMT资料反演解释,同时为地下薄目标层的有效识别提供理论依据.</p>
Wang R Yin C C Wang M Y , et al . CSAMT sensitivity analysis for 1D models
[J]. Progress in Geophys (in Chinese) , 2014 ,29 (3 ):1284 -1291 , doi: 10.6038/pg20140339 .
Magsci
[本文引用: 1]
[9]
李毓茂 , 等 . 电磁频率测深方法与电偶源电磁频率测深量板 [M]. 徐州 : 中国矿业大学出版社 , 2012 . 7 .
[本文引用: 5]
Li Y M , et al. Electromagnetic frequency sounding method and dipole electromagnetic frequency sounding board [M]. Xuzhou : China University of Mining and Technology Press , 2012 .
[本文引用: 5]
[10]
Ziolkowski A Hobbs B Wright D . Multitransient electromagnetic demonstration survey in France
[J]. Geophysics , 2007 ,72 (4 ):197 -207 .
[本文引用: 2]
[11]
[本文引用: 1]
Di Q Y Zhu R X Xue G Q , et al . New development of the Electromagnetic (EM) methods for deep exploration
[J]. Chinese J. Geophys. (in Chinese) , 2019 ,62 (6 ):2128 -2138 , doi: 10.6038/cjg2019M0633 .
[本文引用: 1]
[12]
张文伟 , 底青云 , 雷达 , 等 . 物探新方法——多通道瞬变电磁法在金属矿勘探中的应用
[J]. 黄金科学技术 , 2018 ,26 (1 ):1 -8 .
[本文引用: 2]
Zhang W W Di Q Y Lei D , et al . Multi-channel transient electromagnetic method:a new geophysical method and its application in exploring metallic ore deposits
[J]. Gold Science and Technology , 2018 ,26 (1 ):1 -8 .
[本文引用: 2]
[13]
Strack K M . Exploration with deep transient electromagnetic
[M]. Elsevier , 1992 .
[本文引用: 1]
[14]
汤井田 , 何继善 . 可控源音频大地电磁法及其应用 [M]. 长沙 : 中南大学出版社 , 2005 .
[本文引用: 4]
Tang J T He J S Controlled source audio magnetotelluric method and its application [M]. Changsha , Central South University Press , 2015 .
[本文引用: 4]
[15]
何继善 . 广域电磁法和伪随机信号电法 [M]. 北京 : 高等教育出版社 , 2010 .
[本文引用: 4]
He J S Wide-area electromagnetic method and pseudo-random signal electrical method [M]. Beijing : Higher Education Press , 2010 .
[本文引用: 4]
[16]
Magsci
[本文引用: 2]
利用逆重复<em>M</em>序列伪随机信号良好的自相关特性,提出相关检测地电传输特性的编码电磁勘探法.分析了编码电磁测深原理及参数提取方法.同时记录发送电流信号和多收发距电磁场响应,对源信号和场信号进行相关运算,解卷积分离接收系统响应后可得到大地的频率特性或时间特性,以此实现地电断面的精细探测.在时间域,大地冲激响应和阶跃响应含有丰富的地电信息.通过冲激响应的峰值时间或阶跃响应的晚期渐近值可估计地电阻率分布.基于层状模型的大地冲激响应和阶跃响应正演计算结果表明,编码电磁测深法对大埋深薄层目标体有精细的分辨能力.可应用于能源、矿产资源、水资源、环境地质及工程地质勘察,有良好的应用前景.
Magsci
[本文引用: 2]
[17]
罗维斌 . 伪随机海洋可控源多道电磁测深法研究
[D]. 长沙:中南大学 , 2007 .
[本文引用: 2]
LUO W B . Study on pseudorandom marine controlled-source electromagnetic sounding with multi-offsets
[D]. Changsha: Central South University , 2007 .
[本文引用: 2]
[18]
罗维斌 , 汤井田 , 韩海涛 , 等 . 编码源电磁测深法获取大地全区视电阻率谱的方法及装置,ZL 2016 1 0013962.X
[P/OL]. 2018 -03-23.
[本文引用: 2]
Luo W B Tang J T Han H T , et al . The method and device of obtaining whole zone apparent resistivity spectrum of the earth by coded source electromagnetic sounding, ZL 2016 1 0013962.X
[P/OL]. 2018 -03-23.
[本文引用: 2]
[19]
佟铁钢 . E-Hz广域电磁方法研究
[D]. 长沙:中南大学 , 2010 .
[本文引用: 1]
Tong T G . E-Hz wide area electromagnetic method research
[D]. Changsha: Central South University , 2010 .
[本文引用: 1]
[20]
Chave A D . Numerical integration of related Hankel transforms by quadrature and continued fraction expansion
[J]. Geophysics , 1983 ,48 (12 ):1671 -1677 .
[本文引用: 2]
[21]
Nielsena T I Baumgartnera F . CR1Dmod: A Matlab program to model 1D complex resistivity effects in electrical and electro-magnetic surveys
[J]. Computers & Geosciences , 2006 ,32 :1411 -1419 .
[本文引用: 2]
Principles of electromagnetic methods in surface geophysics
3
2014
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... [1 -2 ,7 -9 ].如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
Foundations of geophysical electromagnetic theory and methods
2
2017
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
The magnetotelluric method: theory and practice
0
2012
Spichak. Electromagnetic sounding of the Earth’s interior: theory, modeling, practice(2nd ed)
1
2015
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
3
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
3
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
多场源地空频率域电磁探测方法研究
2
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
多场源地空频率域电磁探测方法研究
2
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
Handbook of geophysical exploration at sea(2nd ed)
3
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
CSAMT法一维层状介质灵敏度分析
1
2014
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
CSAMT法一维层状介质灵敏度分析
1
2014
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
5
2012
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... [9 ].佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
5
2012
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... [9 ].佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
Multitransient electromagnetic demonstration survey in France
2
2007
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
我国深地资源电磁探测新技术研究进展
1
2019
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
我国深地资源电磁探测新技术研究进展
1
2019
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
物探新方法——多通道瞬变电磁法在金属矿勘探中的应用
2
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
物探新方法——多通道瞬变电磁法在金属矿勘探中的应用
2
2018
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
Exploration with deep transient electromagnetic
1
1992
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
4
2015
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
... 由计算出的水平电偶极源层状模型的各场分量的频率响应,汤井田给出了各场分量全区视电阻率定义[14 ] .本文主要以水平电场Ex 和垂直磁场Hz 分量计算全区视电阻率.为方便论述,此处重写出均匀半空间表面水平电偶源产生的电磁场: ...
4
2015
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
... 由计算出的水平电偶极源层状模型的各场分量的频率响应,汤井田给出了各场分量全区视电阻率定义[14 ] .本文主要以水平电场Ex 和垂直磁场Hz 分量计算全区视电阻率.为方便论述,此处重写出均匀半空间表面水平电偶源产生的电磁场: ...
4
2010
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
4
2010
... 可控源电磁测深法(CSEM)可以说是近十多年来发展最为活跃的近地表地球物理勘探方法之一,在方法原理、观测系统研制及正反演综合解释等方面都有长足进步[1 -4 ] ,主要表现在航空电磁系统、地面电磁系统以及海洋电磁系统的快速发展,且在时间域和频率域,或时、频双域同步拓展[5 ,6 ] .在大深度可控源电磁测深建场方式上,基于水平接地双极源的电磁系统最为广泛[1 -2 ,7 -9 ] .如在时间域,多通道瞬变电磁法(MTEM)和电性源短偏移瞬变电磁法(SOTEM)等电磁探测新技术发展已经成熟[10 ,11 ,12 ,13 ] ;在频率域,可控源音频大地电磁测深法(CSAMT)已成为深地探测有效方法[8 ,14 ] ;广域电磁法只测量水平电场Ex 分量计算全区视电阻率,提高了探测深度和分辨率[15 ] . ...
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 略去繁冗的数学推导[1 -2 ,7 ,9 ,14 -15 ] ,此处直接写出极坐标系统中地表电磁场各分量的表达式为: ...
编码电磁测深
2
2012
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... ,16 ,17 ]. ...
编码电磁测深
2
2012
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... ,16 ,17 ]. ...
伪随机海洋可控源多道电磁测深法研究
2
2007
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... ,17 ]. ...
伪随机海洋可控源多道电磁测深法研究
2
2007
... 在场值观测方面,水平电场和垂直磁场是最主要的电磁场观测分量.航空电磁系统和地空电磁系统主要观测垂直磁场[5 ] ;地面电磁系统则可以同时接收水平电场和垂直磁场;海洋电磁系统还可以测量垂直电场[7 ] .多通道瞬变电磁法(MTEM)只测量轴向水平电场Ex 分量,同步记录激发电流和电场电压时间序列,解卷积获得待探测地电系统冲激响应,由冲激响应峰值时间计算视电阻率等电磁解释参数[10 -12 ,16 -17 ] ;广域电磁法利用水平电场Ex 分量计算全区视电阻率.采用2n [15 ,16 ,17 ] . ...
... ,17 ]. ...
编码源电磁测深法获取大地全区视电阻率谱的方法及装置,ZL 2016 1 0013962.X
2
2018
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 本文给出采用循环互相关算法计算全区视电阻率的方法[18 ] .观测中需要同时记录发送电流和电场或磁场时间序列.当观测场值是水平电场Ex 分量时间序列时,观测值是接收电极间的电位差时间序列, V E x Ex ·MN ,MN 为接收电场的电极间距,采用循环互相关算法可估计出阻抗谱: ...
编码源电磁测深法获取大地全区视电阻率谱的方法及装置,ZL 2016 1 0013962.X
2
2018
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
... 本文给出采用循环互相关算法计算全区视电阻率的方法[18 ] .观测中需要同时记录发送电流和电场或磁场时间序列.当观测场值是水平电场Ex 分量时间序列时,观测值是接收电极间的电位差时间序列, V E x Ex ·MN ,MN 为接收电场的电极间距,采用循环互相关算法可估计出阻抗谱: ...
E-Hz广域电磁方法研究
1
2010
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
E-Hz广域电磁方法研究
1
2010
... 不同的电磁勘探系统观测场分量不同,计算视电阻率的方法也不同.可控源音频大地电磁系统沿用卡尼亚电阻率定义方法,需要同步观测水平电场和水平磁场,在远区观测[14 ] .广域电磁法只测量水平电场Ex 分量计算全区视电阻率,观测范围更大[9 ,15 ,18 ] .李毓茂等研究了电磁频率测深方法并计算了电偶源电磁频率测深量板,给出了不同地电模型水平电场分量Ex 和垂直磁场分量Hz 全区视电阻率曲线图册[9 ] .佟铁钢研究了水平电偶源激发测量垂直磁场的方法,进行了层状模型全区视电阻率数值计算[19 ] . ...
Numerical integration of related Hankel transforms by quadrature and continued fraction expansion
2
1983
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
... 文献[20 ]中,Chave提出了汉克尔变换的数值积分算法.Chave算法的基本思路是,采用高斯求积方法对有限区间积分进行计算,进而结合连分式展开方法加快部分积分和的收敛速度.一反数字滤波法的常规做法,Chave算法使用期望误差(绝对误差/相对误差)来控制计算是继续或是终止.为了直接采用数值求积方法计算式(4),可将积分写成如下部分积分之和: ...
CR1Dmod: A Matlab program to model 1D complex resistivity effects in electrical and electro-magnetic surveys
2
2006
... 层状地质模型的频率域电磁响应(式3,式4)是以Hankel积分形式给出的,而目前的计算方法主要是数字滤波方法[5 -6 ,9 ] .但数字滤波本身计算精度不够高,且滤波系数计算精度取决于具体的计算方法,只有在合适的条件下才有足够的精度.本文采用直接数值积分,将水平电偶源电磁场频率响应所满足的Hankel积分用由Bessel函数零点所分割的子区间上的部分积分的和表示出来,并采用Euler方法加快积分求和的收敛[20 ,21 ] . ...
... 本文采用文献[21 ]介绍的数值积分方法,在matlab计算平台中,预先计算了贝赛尔函数Ji (λr ),i =0,1的300个零点,最初的几个零点之间的区间积分采用matlab 的自适应Simpsons积分函数(QUAD),之后的积分区间根据计算精度,采用自适应Lobatto积分函数(QUADL),积分项的求和采用Euler法加速其收敛,积分的终止条件是最后加入的区间积分项小于设定的容许误差,或者已计算了设定的所有区间数.实际上计算不超过30个过零点区间就可达到所需要的精度. ...