逆时偏移在探地雷达数据处理中的应用

doi:10.11720/wtyht.2019.1319

逆时偏移在探地雷达数据处理中的应用

龚俊波¹, 王洪华¹^,², 王敏玲¹^,², 罗泽明¹

1. 桂林理工大学地球科学学院,广西桂林 541004

2. 广西隐伏金属矿产勘查重点实验室,广西桂林 541004

The application of reverse time migration to GPR data processing

GONG Jun-Bo¹, WANG Hong-Hua¹^,², WANG Min-Ling¹^,², LUO Ze-Ming¹

1. School of Geosciences,Guilin University of Technology,Guilin 541004,China

2. Guangxi Key Laboratory of Hidden Metallic Ore Deposits Exploration,Guilin 541004,China

通讯作者: 王洪华(1986-),博士,讲师,主要从事探地雷达的正演模拟与反演成像研究工作。

收稿日期: 2018-09-6 修回日期: 2019-05-17 网络出版日期: 2019-08-20

基金资助:

国家自然科学基金项目.  41604039
国家自然科学基金项目.  41604102
国家自然科学基金项目.  41574078
广西自然科学基金项目.  2016GXNS FBA380082
广西自然科学基金项目.  2016GXNSFBA380215
广西中青年教师基础能力提升项目.  KY2016YB199
广西有色金属隐伏矿床勘查及材料开发协同创新中心创新团队项目.  GXYSXTZX2017-Ⅱ-5

Received: 2018-09-6 Revised: 2019-05-17 Online: 2019-08-20

作者简介 About authors

龚俊波(1994-),男,硕士研究生,主要从事探地雷达数据处理及偏移成像方面的研究工作。。

摘要

探地雷达(GPR)作为一种浅部地球物理探测技术,在工程检测中得到广泛应用。为提高雷达资料的解译精度,本文将逆时偏移算法应用于实测数据处理和解释。首先,从Maxwell方程组出发推导了二维TM模式下电磁波时域有限差分(FDTD)方程、给出了CFL数值稳定性条件和数值频散关系。在此基础上,阐述了GPR逆时偏移成像原理及零时刻成像条件公式,并编制了相应GPR逆时偏移程序。为验证逆时偏移对提高成像精度的有效性,设置了两个典型空洞模型,将逆时偏移程序应用于空洞模型GPR正演数据的处理,并与克希霍夫偏移结果进行对比分析。结果表明:相比于克希霍夫偏移结果,逆时偏移剖面中反射波归位更加准确,绕射波收敛更加完全。最后,将逆时偏移算法应用于实测数据处理中,精确圈定了地下管线的空间位置,为道路的后续施工与处置提供了科学依据。

关键词： 探地雷达 ; 逆时偏移 ; 数据处理 ; 管线探测

Abstract

As a shallow geophysical detection technology,Ground Penetrating Radar (GPR) has been widely used in engineering detection.In order to improve the interpretation accuracy of radar data,this paper introduces reverse time migration (RTM) to process and interpret GPR observed data.Firstly,Finite Difference Time Domain (FDTD) equations of electromagnetic wave in two-dimensional TM mode,CFL numerical stability condition and dispersion relations are derived from Maxwell equations.On such a basis,the principle of RTM and the formula of zero time imaging condition are elaborated,and the corresponding program of RTM is compiled.Two typical voids models are established.The simulated data of two typical void GPR models are processed by RTM to verify the validity of GPR RTM in improving imaging resolution.Compared with Kirchhoff migration result,the homing of reflected wave is more accurate and the convergency of diffracted wave is more complete in the RTM image.Finally,RTM is applied to processing the observed data,which is observed on the underground pipeline.The pipeline is accurately delineated,which provides a scientific basis for the follow-up construction and disposal of the road.

Keywords： ground penetrating radar (GPR) ; reverse time migration (RTM) ; data processing ; pipeline detection

PDF (2734KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

龚俊波, 王洪华, 王敏玲, 罗泽明. 逆时偏移在探地雷达数据处理中的应用. 物探与化探[J], 2019, 43(4): 835-842 doi:10.11720/wtyht.2019.1319

GONG Jun-Bo, WANG Hong-Hua, WANG Min-Ling, LUO Ze-Ming. The application of reverse time migration to GPR data processing. Geophysical and Geochemical Exploration[J], 2019, 43(4): 835-842 doi:10.11720/wtyht.2019.1319

0 引言

探地雷达(ground penetrating radar,GPR)作为一种重要的浅部地球物理探测技术,以其无损性、高分辨率、操作简便等优点被广泛应用于工程勘察^[1,2]、考古调查^[3]、管线探测^[4]等众多领域。由于地下介质分布的随机性和电磁波传播规律的复杂性,原始采集的雷达数据中存在大量的散射波、绕射波等干扰。应用常规数据处理方法(如零时校正、滤波^[5]、增益^[6]等)对雷达剖面进行处理虽然可以提高目标体反射波的能量,但难以精确给出探测目标体埋深、尺寸等工程检测中最为关心的工程指标。偏移作为一种实测数据与地下真实结构转换的重要技术,可将目标体产生的反射波准确归位,绕射波自动收敛到其真实空间位置,在GPR数据处理中得到广泛应用^[7]。传统的偏移方法如绕射叠加法、克希霍夫偏移法的偏移精度低;频率—波速偏移法难以适合横向分布不均匀的速度模型,且存在倾角限制^[8]。逆时偏移基于双程波动方程,能够精确地处理沿任意方向传播的电磁波,精准地将电磁波场归位到其真实的地下空间位置,实现绕射波的完全收敛和反射波的准确归位,具有精度高、相位准确、不受横向变速和高陡倾角影响的优点^[9]。

早在1992年,Fisher等^[10]根据地震波与电磁波传播规律的相似性,从理论上论证了逆时偏移应用于GPR数据处理中的可行性和有效性;鲁兴林和钱荣毅^[11] 通过对比两个典型GPR模型的正演数据的逆时偏移和克希霍夫偏移剖面,说明了逆时偏移算法的成像精度要远优于克希霍夫偏移算法;周辉等^[12]为克服地形对GPR信号的影响,将逆时偏移应用于起伏地表探地雷达数据处理中,有效改善了目标体的成像精度;傅磊等^[13]开展了机载雷达二维的逆时偏移成像研究;底青云^[14]等考虑电阻率对GPR信号的影响利用有限元法实现了衰减介质的GPR逆时偏移;薛桂霞^[15]将逆时偏移应用于GPR实测数据的处理与解释中;韩波^[16]等采用遗传算法构建偏移速度模型,进一步提高了逆时偏移成像的精度;雷文太等^[17]实现了非均匀空间采样下的表层穿透雷达逆时偏移成像;石明^[18]等采用基于交叉微分算子的差分逆时偏移,提高了GPR在高陡起伏地形情况下的偏移成像精度。

上述研究大都侧重于逆时偏移理论研究,文中针对GPR管线探测问题,将逆时偏移应用于实测数据处理中。首先,基于时域有限差分法(finite difference time domain,FDTD)和零时刻成像条件原理,利用Matlab软件编制了GPR逆时偏移程序。然后,建立了2个典型的空洞模型,利用GPR逆时偏移算法对其正演信号进行逆时偏移成像,并与其克希霍夫偏移剖面进行对比,验证了逆时偏移在提高雷达剖面分辨率和成像精度方面的优越性。最后,将逆时偏移算法应用于地下管线的实测数据处理中,大大提高了管线定位的精度,为测区后期施工提供科学的技术支持。

1 时域有限差分法原理

根据电磁波理论^[19],假设地质体走向为Z轴,二维地电条件下,GPR电磁波探测通常采用的TM模式对应的电磁波方程组为:

(1)

\{\begin{array}{l} \frac{\partial E_{z}}{\partial y} = - μ \frac{\partial H_{x}}{\partial t} - σ_{m} H_{x}, \\ \frac{\partial E_{z}}{\partial x} = μ \frac{\partial H_{y}}{\partial t} + σ_{m} H_{y}, \\ \frac{\partial H_{y}}{\partial x} - \frac{\partial H_{x}}{\partial y} = ε \frac{\partial E_{z}}{\partial t} + σ E_{z} 。 \end{array}

式中:H_x、H_y分别表示磁场在x、y方向上的磁场强度,A/m;E_z表示电场在z方向上的电场强度,V/m;σ、σ_m、ε、μ分别为电导率(S/m)、导磁率(Ω/m)、介电常数(F/m)、磁导系数(H/m)。

采用Yee网格对计算区域进行离散,并用中心差商代替微商,把连续变量离散化,可推导式(1)对应的时空域迭代方程为^[19]:

(2)

H_{x}^{n + 1 / 2} (i, j + 1 / 2) = CP (m) \cdot H_{x}^{n - 1 / 2} (i, j + 1 / 2) - CQ (m) \cdot \frac{E_{z}^{n} (i, j + 1) - E_{z}^{n} (i, j)}{Δ y},

(3)

H_{y}^{n + 1 / 2} (i + 1 / 2, j) = CP (m) \cdot H_{y}^{n - 1 / 2} (i + 1 / 2, j) + CQ (m) \cdot \frac{E_{z}^{n} (i + 1, j) - E_{z}^{n} (i, j)}{Δ x},

(4)

\begin{array}{l} E_{z}^{n + 1} (i, j) = CA (m) \cdot E_{z}^{n} (i, j) + CB (m) \cdot [\frac{H_{y}^{n + 1 / 2} (i + 1 / 2, j) - H_{y}^{n + 1 / 2} (i - 1 / 2, j)}{Δ x} \\ - \frac{H_{x}^{n + 1 / 2} (i, j + 1 / 2) - H_{x}^{n + 1 / 2} (i, j - 1 / 2)}{Δ y}] 。 \end{array}

式(2)~(4)中:Δx、Δy分别为x、y方向上的空间步长,Δt为时间步长,i、j分别表示x、y方向上的网格节点,n表示迭代时间步数,m与其所在等式左端电场或磁场的空间位置一致,CP(m)、CQ(m)、CA(m)、CB(m)分别表示与其所在等式左端电场或磁场所处空间位置的介质参数,其计算公式可参考文献[19、20]。

利用FDTD进行GPR正演模拟时,由于采用中心差分近似代替连续偏导数,使得电磁波在计算空间中传播时会出现数值频散现象^[20]。为克服上述数值频散现象,一般可选用小空间和时间步长来进行压制,但小步长不可避免带来计算时间的增大。为在时间与空间步长的选择取平衡,二维地电结构条件下,时间和空间步长应满足的CFL(courant-friedrich-levy)稳定条件为:

(5)

Δ t \leq \frac{1}{c \sqrt[]{{(1 / Δ x)}^{2} + {(1 / Δ y)}^{2}}} 。

式(5)中,c=1/ $\sqrt[]{εμ}$ 为电磁波在介质中传播速度,空间步长的选择需满足:

(6)

\min (Δ x, Δ y) \leq λ_{\min} / 10,

式(6)中,λ_min为电磁波在介质中传播的最小波长。

此外,为充分吸收模型边界处的超强反射,在模型外边界施加完全匹配层(perfectly matched layer,PML)^[21],从而使得模型外边界的超强反射波被充分吸收。

2 基于零时刻成像条件的GPR逆时偏移成像方法

GPR逆时偏移的基本原理是将地表记录到的接收点电磁波场在时间轴上进行逆向传播,当电磁波场逆推至零时刻,则所有反射波和绕射波的能量都回到最初被反射和绕射的空间位置,然后应用成像条件可获得最终的偏移剖面^[22]。依据处理资料的不同,逆时偏移可分为多偏移距数据和共偏移距数据的逆时偏移,分别类似于弹性波叠前和叠后逆时偏移。考虑到GPR野外数据采集通常采用剖面法,即等偏移距观测方式,因收发天线间距小,可当作自激自收雷达剖面,可采用叠后逆时偏移算法对其进行处理。

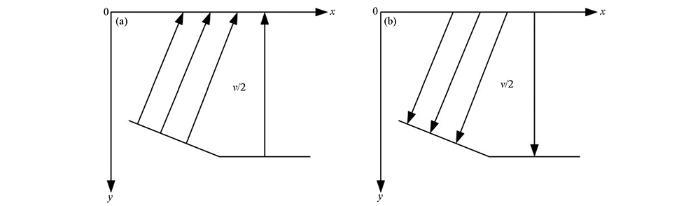
利用零时刻成像条件对等偏移距GPR数据进行逆时偏移成像的基本原理是将等偏移距GPR雷达剖面看作是自激自收雷达剖面,同时将地下反射界面上的任意一点均看作一个爆炸源(图1a)。当地面上t=0时刻,爆炸反射面激发的波前与其反射界面形状位置一致,并以电磁波实际速度的1/2倍向上传播至地面观测点,此时所得的地面记录就相当于自激自收雷达剖面;反之,地面接收到的雷达剖面逆时延拓至t=0时,此时反射和绕射的能量归位于其最初产生的位置,即可实现逆时偏移成像(图1b)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 共偏移距GPR逆时偏移成像示意

a—爆炸反射面模拟;b—爆炸反射面成像

Fig.1 Sketch map of reverse time migration with common offset GPR data

a—simulation of exploding reflector;b—imaging of exploding reflector

若用 $E_{z}^{n + 1}$ (i,1)Yee网格离散后的实测数据表示并作为边值条件,从最大时刻n+1以介质半速度进行逆时外推,其电磁场逆时外推公式可表示为:

(7)

H_{x}^{n - 1 / 2} (i, j + 1 / 2) = \frac{2 μ (m) + σ_{m} (m) Δ t}{2 μ (m) - σ_{m} (m) Δ t} \cdot H_{x}^{n + 1 / 2} (i, j + 1 / 2) + \frac{2 Δ t}{2 μ (m) - σ_{m} (m) Δ t} \cdot \frac{E_{z}^{n} (i, j + 1) - E_{z}^{n} (i, j)}{Δ y}

(8)

H_{y}^{n - 1 / 2} (i + 1 / 2, j) = \frac{2 μ (m) + σ_{m} (m) Δ t}{2 μ (m) - σ_{m} (m) Δ t} \cdot H_{y}^{n + 1 / 2} (i + 1 / 2, j) - \frac{2 Δ t}{2 μ (m) - σ_{m} (m) Δ t} \cdot \frac{E_{z}^{n} (i + 1, j) - E_{z}^{n} (i, j)}{Δ x}

(9)

\begin{array}{l} E_{z}^{n} (i, j) = \frac{8 ε (m) + σ (m) Δ t}{8 ε (m) - σ (m) Δ t} \cdot E_{z}^{n + 1} (i, j) - \frac{2 Δ t}{8 ε (m) - σ (m) Δ t} \cdot [\frac{H_{y}^{n + 1 / 2} (i + 1 / 2, j) - H_{y}^{n + 1 / 2} (i - 1 / 2, j)}{Δ x} \\ - \frac{H_{x}^{n + 1 / 2} (i, j + 1 / 2) - H_{x}^{n + 1 / 2} (i, j - 1 / 2)}{Δ y}] + E_{z}^{n + 1} (i, 1) \end{array}

当逆时外推至零时刻时,E_z的空间分布即为逆时偏移成像剖面,其表达式为:

(10)

I (x, y) = E_{z}^{1} (i, j) 。

3 理论算例

为验证基于零时刻成像条件的GPR逆时偏移算法及程序的正确性,建立了2个典型的空洞模型,利用编制的GPR逆时偏移程序对该模型的正演数据进行逆时偏移成像,并与克希霍夫偏移剖面进行对比,以验证逆时偏移成像结果的优越性。

3.1 模型一

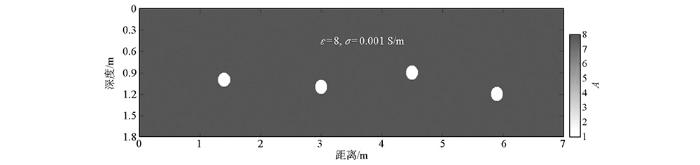
模型一是大小为7 m×1.8 m的GPR空洞模型,如图2所示。模型中充填混凝土介质,其相对介电常数为8,电导率为0.001 S/m。模型中埋有四个半径为0.1 m的圆形空洞,圆心坐标分别为(1.4 m,1.0 m),(3.0 m,1.1 m),(4.5 m,0.9 m),(5.9 m, 1.2 m)。利用FDTD正演算法对该模型进行正演计算时的空间步长为0.005 m×0.005 m,时间步长为0.005 ns,时窗长度为35 ns,激励源采用中心频率为250 MHz的雷克子波。采用剖面法观测方式进行正演,其收发天线间距为0.05 m,测量点距为 0.05 m。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 模型一示意

Fig.2 Schematic map of GPR model 1

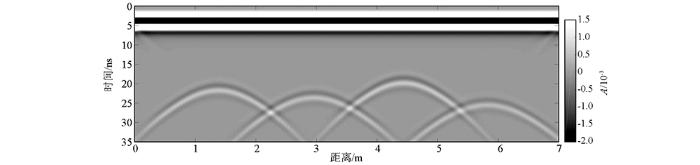
图3为模型一GPR正演剖面图,由图可见:圆形空洞顶部产生的双曲线绕射波清晰可见,绕射波双曲线两翼向两侧延伸,大大超过了圆形空洞直径。由于双曲线绕射波的存在,从GPR正演剖面中难以直接获得圆形空洞的位置、埋深和大小等几何参数。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 模型一正演剖面

Fig.3 Simulated profile of model 1

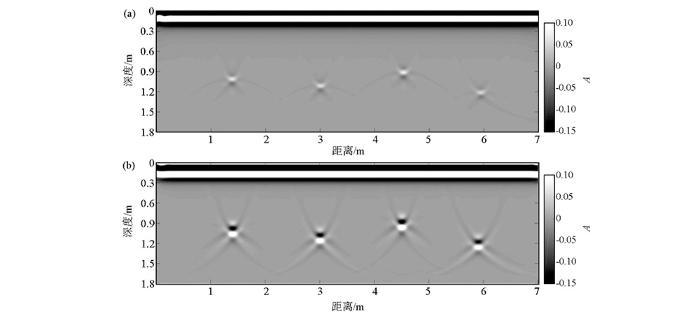
分别利用克希霍夫偏移和逆时偏移成像算法对图3所示的正演数据进行偏移成像,获得如图4所示的偏移剖面。由图4可知,两种偏移算法都能较好地对四个圆形空洞进行成像,成像剖面中的反射波和绕射波基本上得到收敛,且收敛位置与圆形空洞的真实位置吻合。对比图4a、4b可知,相比于克希霍夫偏移结果,逆时偏移剖面中的反射波归位更准确,绕射波更收敛于空洞的真实空间位置。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 模型一正演数据的克希霍夫偏移和逆时偏移剖面

a—克希霍夫偏移剖面;b—逆时偏移剖面

Fig.4 Kirchhoff migration and reverse time migration profiles of model 1

a—kirchhoff migration profile;b—reverse time migration profile

3.2 模型二

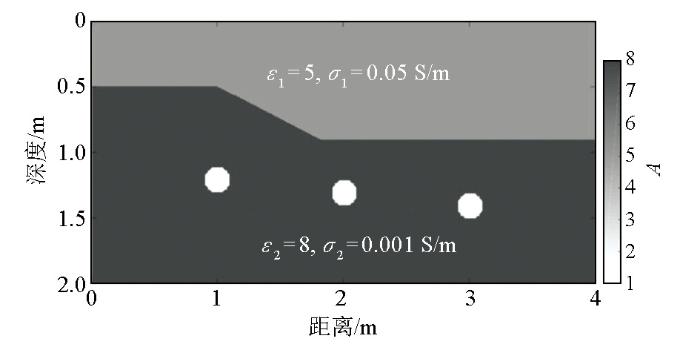
图5是大小为4 m×2 m的GPR模型二示意图,模型被一条阶梯状界面分为上下两层。其中,上层介质的相对介电常数为5,电导率为0.05 S/m,下层介质的相对介电常数为8,电导率为0.001 S/m。下层介质中埋有三个半径为0.1 m的圆形空洞,圆心坐标分别为(1.0 m,1.2 m),(2.0 m,1.3 m),(3.0 m,1.4 m)。利用FDTD正演算法对该模型进行正演计算时的参数与模型一相同。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 模型二示意

Fig.5 Schematic map of GPR model 2

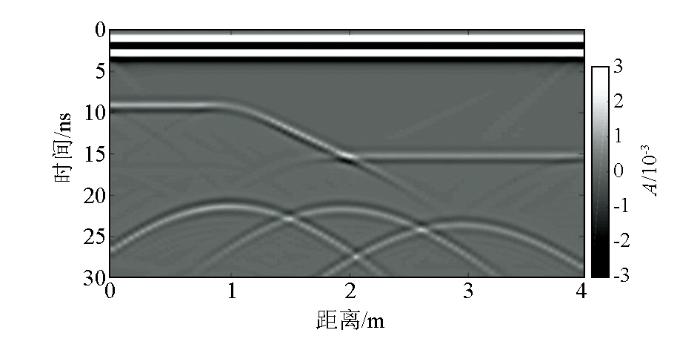
图6为模型二GPR正演剖面,由图可见:阶梯状反射界面产生的反射波和三个圆形空洞产生的绕射波清晰可见,其中倾斜反射界面的两端出现绕射现象,圆形空洞的绕射波随埋深的增大,出现时间变长,且双曲线延伸范围较大,已经超过圆形空洞的真实大小。因而,直接从正演剖面图中判断阶梯状界面和圆形空洞的位置和大小非常困难。

利用克希霍夫偏移和逆时偏移算法对图6所示的GPR正演剖面进行处理,获得如图7所示的偏移剖面,其中图7a为克希霍夫偏移成像剖面,图7b为逆时偏移剖面。由图可知:两种偏移算法都能对阶梯状界面和圆形空洞异常体进行较好的成像,阶梯状反射界面和圆形空洞的成像位置与真实位置相符。对比图7a和7b可知:相比克希霍夫偏移结果,逆时偏移结果中反射界面中部倾斜位置的成像更清晰,两个端点成像效果更好,如7b中箭头所示;圆形空洞绕射波收敛更好,绕射波能量能更好地聚焦于真实位置。通过分析上述图件可知:相比于克希霍夫偏移,逆时偏移对地下结构的成像效果更好,精度更高,利于定位圆形空洞的埋深、大小等信息,大大提高地下空洞的成像精度。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 模型二GPR正演剖面

Fig.6 Simulated profile of model 2

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 模型二正演数据的克希霍夫偏移及逆时偏移剖面

a—克希霍夫偏移剖面;b—逆时偏移剖面

Fig.7 Kirchhoff migration and reverse time migration profiles of model 2

a—kirchhoff migration profile;b—reverse time migration profile

4 实测数据的逆时偏移成像

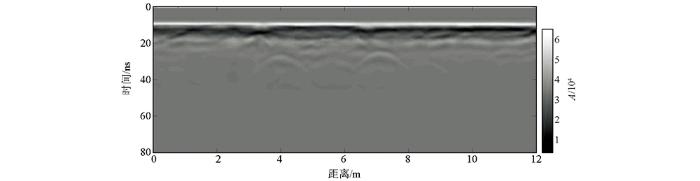
为验证逆时偏移算法应用于GPR实测数据处理中的效果,文中利用RAMAC CU-2 型GPR系统对某道路进行探测,并将逆时偏移应用于数据处理中。测区场地较为平坦,地下主要有混凝土层、回填土层和地基层,其中回填土层中的管线众多,相互交错,且管线密集,探测难度很大。实际探测时采用中心频率为250 MHz的屏蔽天线,时窗长度设置为80 ns,测线与管线走向垂直布设,由于线路不长,故采用点测模式进行数据采集,点距为0.1 m,即每米采集10道信号。图8为测线1原始雷达剖面图,由于高频电磁波的衰减,在20~40 ns范围内由管线产生的双曲线反射波形非常微弱; 且在约20 ns处由混凝土层与回填层界面产生的反射波近似水平,但反射波能量非常微弱,不易被识别。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 测线1雷达原始数据剖面

Fig.8 Original GPR data profile of survey 1

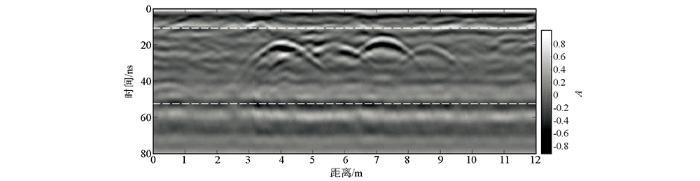
利用零时校正、直流滤波、带通滤波、自动增益等处理方法对图8进行处理后,获得的雷达剖面如图9所示。由图可见:相比于图8,经过常规处理后的雷达剖面中管线产生的双曲线清晰、易被识别,可对管线的水平位置分布和埋深进行大致判断,但是由于双曲线的两翼延伸范围较大,难以对管线真实空间位置进行精确定位。此外,混凝土层与回填层的界面、回填层与地基层的界面反射波都清晰可见,但由于电磁波在地下介质传播时,高频成分衰减严重,导致 50 ns处的反射波持续时间更长,难以较精确的定位界面的埋深。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 常规处理结果

Fig.9 Results of conventional data processing

利用克希霍夫偏移和逆时偏移算法分别对图9进行偏移成像,获得的成像剖面如图10所示。由图可见:经偏移处理后,绕射波收敛较好,反射波能量基本得到归位,可从剖面图中较好地识别管线及混凝土层与回填层、回填层与地基层两个反射界面的空间位置。对比图10a、10b可知:相比于克希霍夫偏移,逆时偏移中反射波能量更聚焦于地下管线及两个反射界面的真实空间位置,剖面分辨率更高,更利于探测结果的解释工作。结合测区地质资料与雷达剖面可做如下判断:测线1上有四条并行且规格一样的污水管道,其材质为钢,直径约为400 mm,其中心水平位置大约分别在4.1、5.7、7.2、8.6 m处,顶部埋深大约介于0.8~1.1 m;混凝土厚度约为0.4 m,回填层厚度约为2.2 m。由此可见:通过对实测数据进行偏移处理可大大提高雷达剖面的分辨率,有助于目标体的精确定位;与克希霍夫偏移剖面相比,逆时偏移剖面的精度更高,分辨率更好,其结果可更好地为测区的后续施工提供科学依据。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 克希霍夫偏移及逆时偏移剖面

a—克希霍夫偏移剖面;b—逆时偏移剖面

Fig.10 Kirchhoff migration and reverse time migration profiles

a—kirchhoff migration profile;b—reverse time migration profile

5 结论

1)从Maxwell方程出发,推导了二维TM模式下GPR时域有限差分格式,探讨了FDTD计算过程中的CFL数值稳定性条件和数值频散关系。在此基础上,阐述了GPR逆时偏移成像原理及零时刻成像条件公式,并编制了相应的GPR逆时偏移程序。

2)两个空洞模型的正演数据及实测数据的克希霍夫偏移和逆时偏移结果表明:逆时偏移的成像结果要明显优于克希霍夫偏移结果,逆时偏移剖面中的地下目标体成像结果与其真实位置高度吻合,成像精度更高,可更好地指导后续的雷达资料解释工作。

(本文编辑:叶佩)

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

范占锋, 李天斌, 孟陆波 .

探地雷达在公路隧道超前地质预报中的应用

[J]. 物探与化探, 2010,34(1):119-122.

Magsci [本文引用: 1]

探地雷达作为公路隧道超前地质预报的手段之一，对预报掌子面前方岩体的微细结构能起到很重要的作用，同时可以作为隧道勘察结果的进一步认识和补充。以新扎沟隧道为例，利用SIR20探地雷达并结合工程地质方法,对节理破碎带和地下水成功地做出了预测。对这几种不良地质体雷达反射波的频谱特征做了简要研究，为以后探地雷达探测数据的解译积累了经验。

Fan Z

, Li T

, Meng L

Advanced geological forecast of application of GPR in road tunnel

[J]. Geophysical and Geochemical Exploration, 2010,34(1):119-122.

Magsci [本文引用: 1]

[2]

王正成, 吴晔 .

探地雷达隧道衬砌质量检测技术

[J]. 物探与化探, 2013,32(6):1152-1156.