0 引言
我国整修加固堤坝长度近50×104 km,修建大中小型水库共9万多座,总库容约9 000×108m3[1]。由于自然灾害等原因导致的土石堤坝隐患,严重威胁着人民的生命和财产安全,为此实现对土石堤坝隐患的监测和预报成为了一项重要的研究课题。在各类探测方法中,地球物理方法以它无损、便捷的探测方式,全面的探测结果,受到了极大的关注。高密度直流电阻率法是一种常用的勘探地球物理方法,其通过在地表上发射和接收电位信号,快速得到地下电性差异,并且不会对探测区域产生损害[2],被广泛应用到坝基勘察和堤坝安全调查等方面[3,4,5,6]。目前高密度直流电阻率法在堤坝上的应用仅是对隐患与坝体本身电性差异的常规探测,对于尺度较小的土石堤坝隐患,受仪器和方法的限制,很难在探测效果上有明显的提高。时移高密度电阻率法是在常规电阻率法的基础上提出的一种精细探测方法,它对同一区域进行长时间重复连续的观测,监测目标区域的电性结构变化。由于时移监测是着眼于目标电性特征的相对变化,因此相对于常规方法在观测效果上有着显著优势[7]。该方法目前多用于监测岩土、滑坡等水文地质方面。2011年,Arora T、 Ahmed S应用时移电阻率法监测花岗岩,分析含水层的渗流补给特征[8]; 2012年,Travelletti J、 Sailhac P、 Malet J P等通过时移电阻率法监测黏土页岩滑坡,研究内部的水流变化规律[9];2018年,李飞、程久龙等对时移高密度电法在覆岩精细探测方面进行了研究,分析了覆岩变形破坏与电阻率变化间的关系[10]。
在堤坝监测方面,国外已有学者提出应用时移电阻率法监测堤坝隐患变化。2005年,Sjödahl P等通过对瑞典某尾矿坝进行电阻率法安全调查,论证了重复多次的观测方法可以比常规单独观测解释得到更多的信息[11];2011年,Boleve A、Janod F等通过使用示踪剂注入岩土的方式,在实验室模拟时移电阻率监测的变化规律,并对法国某堤坝(已证实出现了渗流)的渗漏进行验证,取得令人满意的效果[12]。但是,土石堤坝隐患时移监测大多数尚处在试验研究阶段,针对它的理论研究也主要是基于一维或二维介质模型,无法准确模拟堤坝三维地电结构。三维数值模拟方法主要有有限元、有限差分和有限体积等,基于非结构四面体网格有限元法在模拟复杂地电模型方面较其他方法更具有优势[13],被应用到多种勘探地球物理方法中。2009年,李勇、林品荣等将非结构网格应用到复杂地形的直流电阻率法三维有限元正演中,并利用对称超松弛预条件共扼梯度迭代算法提高解的精度[14];2017年,王亚璐、底青云等在CSAMT有限元数值模拟中应用非结构化网格,通过加入散度条件来约束电场,避开了源的奇异性问题,并减少了计算区域[15];2015年,杨军,刘颖等采用非结构网格模拟复杂海底地形和异常结构的海洋CSEM响应,探究了海底地形对电场分布的影响等[16]。为了能够更加准确地反映坝体结构和隐患对电场分布变化的影响,弥补土石堤坝隐患时移监测理论研究的不足,本文基于非结构网格三维有限元正演数值模拟方法,模拟土石堤坝时移监测电位信号地表分布,在更加精细的模型基础上研究时移监测的特征规律,推动非结构三维有限元在堤坝隐患时移监测方面的应用。
1 非结构三维有限元正演理论
1.1 稳定场控制方程及边界条件
直流电阻率法是通过发射装置向地下提供直流电,并在地下形成稳定的电流场。对于单个点电源,将欧姆定律微分形式j=σE以及电场强度与电位的关系E=-▽u,同时取散度可得
其中:E表示电场强度,u表示电位,j表示电流密度, σ表示电导率,q表示电荷密度。
对于电源处,电荷密度无限大,非电源处的电荷密度均为零,故引入狄莱克函数[17],
式中(x0,y0,z0)为点电源位置坐标。在使用有限元法进行数值模拟时,其内部的连续性条件一般是自动满足,因此只需研究各个区域外表面的需要满足的边界条件。在地面和空气的交界面,采用诺依曼边界条件:
对于无限远的边界,可以设定电流密度在此边界上的法向分量为0或者是电势为0,但是这两种条件都有限制性,为了消除限制,采用混合边界条件[18]:
θ为测点处边界的法向量与点源到测点的向量的夹角。
1.2 非结构有限元分析
采用Garlerkin加权余值法,对式(2)进行标量有限元离散[17]:
Nj为标量插值函数。将边界条件(3)、(4)代入式(5):
(6)
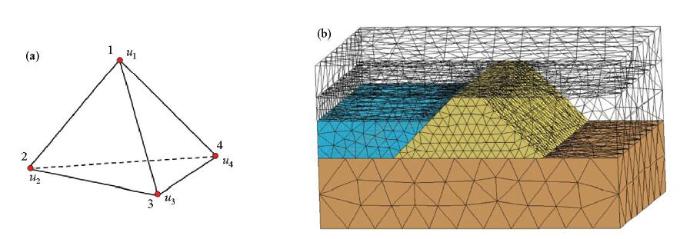
式中,$\partial$ΩM为无穷远处的边界。为了更加精确地逼近堤坝隐患模型,本文采用非结构单元进行剖分,如图1所示。将自由度赋于节点上,在单元内任意位置的电势可以表示为
对所有剖分的网格进行单元分析之后,形成大型线性稀疏方程组,采用MKL库中的并行求解器PARDISO对方程组进行直接求解。
图1
1.3 时移视电阻率成像计算
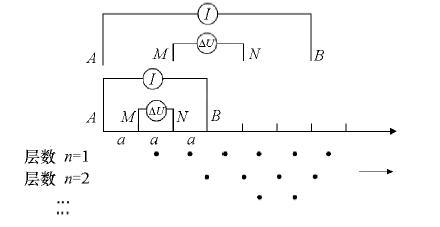
其中:a为电极距离,ΔU为电极MN间的电位差,I为供电电流大小。
图2
时移视电阻率成像是在原有的视电阻率计算基础上增加时间变化的因素,即对同一区域进行多期的或连续性的全寿命周期观测,将该区域不同时刻得到的视电阻率结果相比较,进而研究堤坝视电阻率随时间变化的响应特征。根据时移成像的理论,可以得到时移视电阻率Δρs计算公式:
式中:
2 程序正确性验证
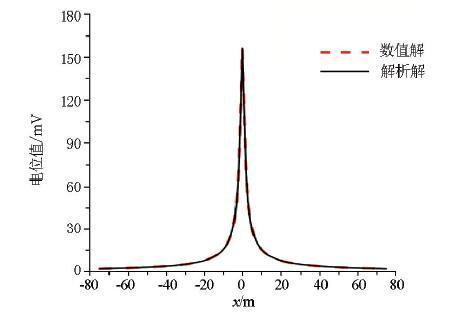
采用具有解析解的半空间模型,对单级装置验证本文正演算法的正确性。模型参数设置如下:半空间电阻率100 Ω·m,供电电极正极位于地表下方1 m,在电极正上方地表左右对称布置151个测点,测点间距1 m,电流10 A。空间网格剖分最小单元尺寸0.05 m,剖分范围40 km×40 km×40 km,总网格节点数34.6万。计算结果(图3)显示,三维正演数值解与解析解具有较高的吻合度,表明三维正演程序的正确性。
图3
3 三维堤坝隐患模型分析
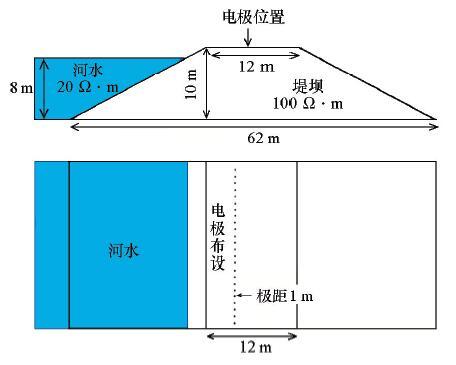
图4
3.1 管状渗漏
图5
图5
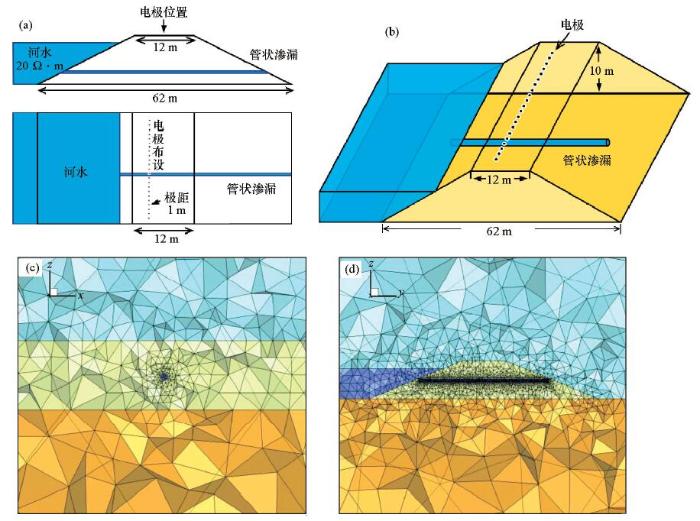
管状渗漏模型及网格剖分示意
a—管状渗漏平面示意;b—管状渗漏立体示意;c—网格剖分xz剖面; d—网格剖分yz剖面
Fig.5
Schematic diagram of tubular leakage model and meshing
a—schematic diagram of the tubular leak plane;b—stereoscopic diagram of tubular leakage;c—mesh split xz profile;d—mesh split yz profile
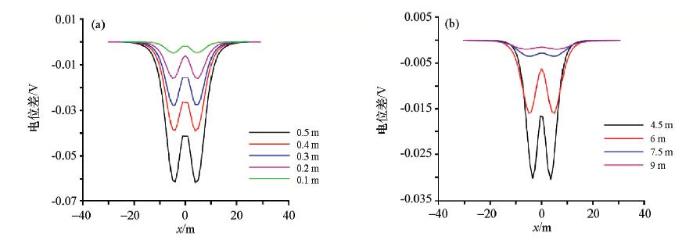
由于堤坝隐患会因自然环境等因素发展变化,因此可以通过时移高密度电法来监测堤坝隐患的相对变化。基于上述管状渗漏模型,设置直径分别为 0.1、0.2、0.3、0.4、0.5 m,埋深距坝顶6 m以及直径为0.2 m,埋深分别为4.5、6、7.5、9 m的两组不同变化方式的管体模型,电阻率10 Ω·m,模拟隐患不同的变化趋势,供电电流10 A。
图6
图6
不同直径(a)和不同深度(b)管状渗漏的电位曲线
Fig.6
Potential curves for tubular leaks at different diameters (a) and at different depths (b)
图7
图7
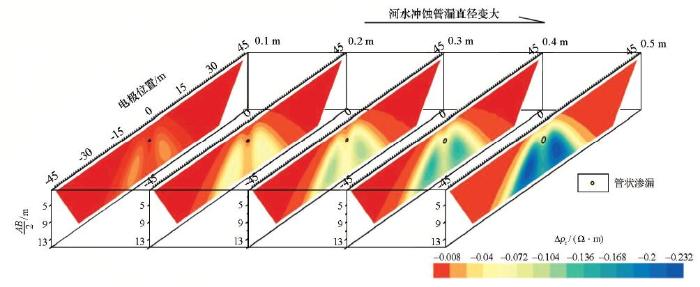
不同直径管状渗漏的时移视电阻率剖面
Fig.7
Time-lapse resistivity profile of tubular leaks of different diameters
图8
图8
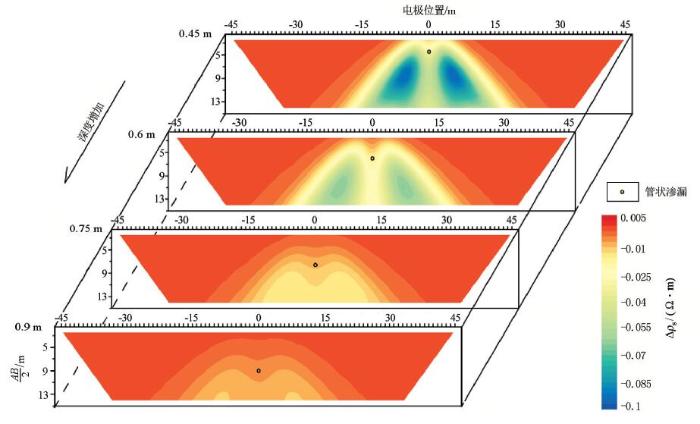
不同埋深管状渗漏的视电阻率剖面
Fig.8
Apparent resistivity profile of different buried deep tubular leaks
3.2 层状渗漏
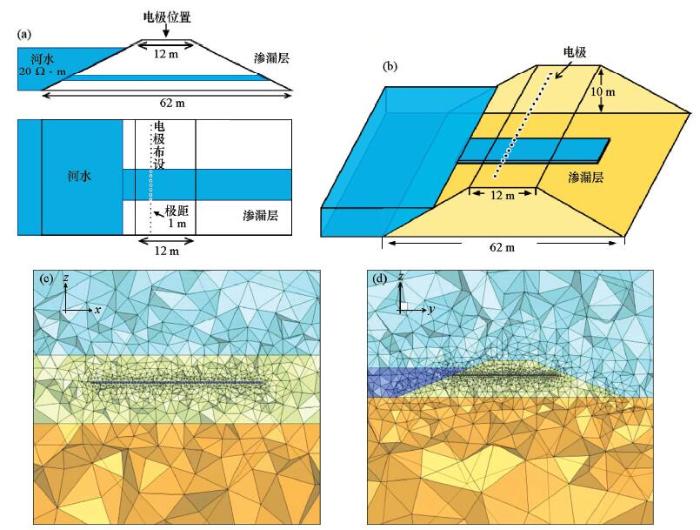
层状渗漏主要是由于松软层或坝体本身填充杂物等因素的影响,使堤坝出现层状的渗漏现象,为此在堤坝模型的基础上设置层状渗漏模型进行研究分析。如图9所示,在堤坝内部设置一个渗漏层,模拟上游河水渗入大坝内部,甚至贯穿整个堤坝,采用与管状渗漏同样的网格剖分方式。基于上述层状渗漏模型,同样设置厚度分别为0.15、0.2、0.25、0.3 m,埋深距坝顶6 m以及厚度0.25 m,埋深分别为4.5、6、7.5、9 m,长度62 m,宽25 m的两组不同变化方式的层状模型,电阻率10 Ω·m,模拟渗漏层不同的变化趋势,供电电流10 A。
图9
图9
层状渗漏模型及网格剖分示意
a—层状渗漏平面示意;b—层状渗漏立体示意;c—网格剖分xz剖面; d—网格剖分yz剖面
Fig.9
Layered leakage model and meshing diagram
a—plane leakage schematic diagram;b—three-dimensional schematic diagram of layered leakage;c—mesh split xz profile;d—mesh split yz profile
图10
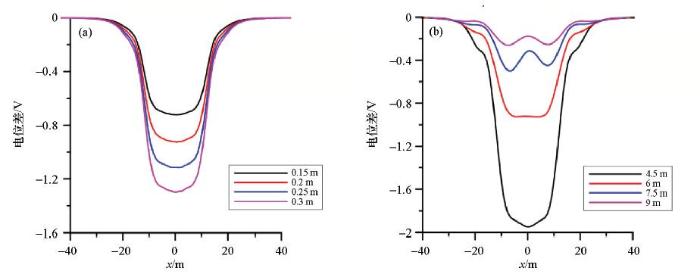
图10
不同层厚(a)、不同深度(b)层状渗漏的电位变化曲线
Fig.10
Potential change graph of layer thickness change(a) and depth change(b)
图11
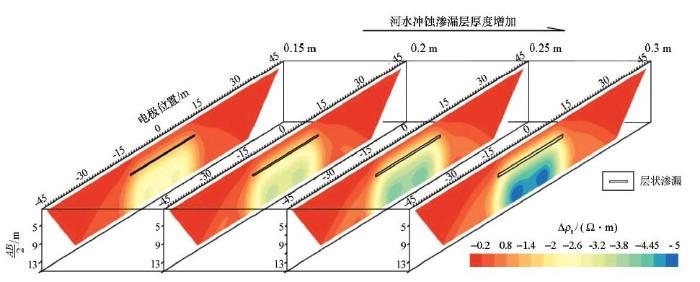
图11
不同厚度层状渗漏的视电阻率剖面
Fig.11
Apparent resistivity of thickness 0.15 m, 0.2 m, 0.25 m, 0.3 m
图12
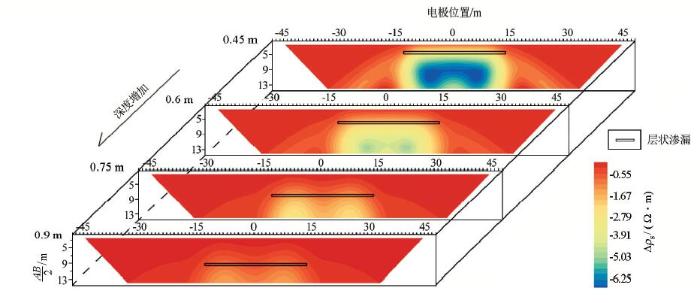
图12
不同埋深层状渗漏的视电阻率剖面
Fig.12
Apparent resistivity map of buried depth 4.5 m, 6 m, 7.5 m, 9 m
3.3 裂缝隐患
图13
图13
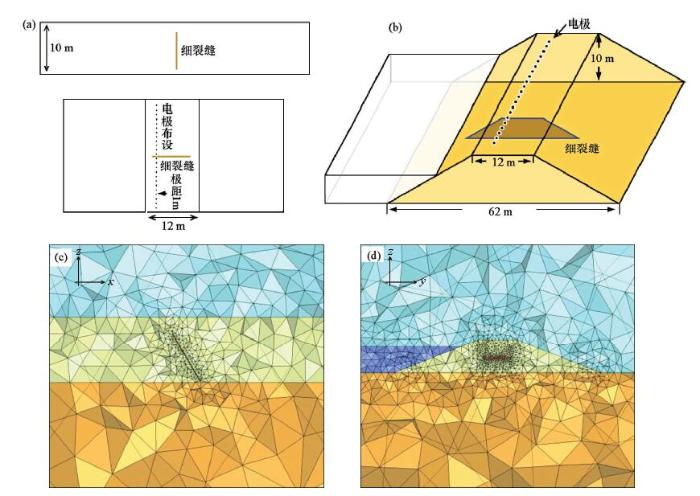
堤坝细裂缝示意
a—细裂缝平面示意;b—细裂缝立体示意;c—网格剖分xz剖面; d—网格剖分yz剖面
Fig.13
Schematic diagram of fine cracks in the dam
a—fine crack plane diagram;b—three-dimensional schematic diagram of fine cracks;c—mesh split xz profile;d—mesh split yz profile
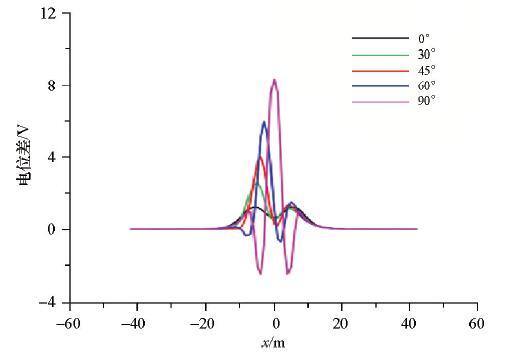
裂缝厚设置为0.1 m,直立形态下,上顶宽10 m,下底宽10 m,长8 m,电阻率设为108 Ω·m以模拟裂缝中的空气,中心埋深在距离坝顶部6 m深处,选取0°~90°的倾角进行数值模拟计算。电流大小为10 A,随着倾角的增加电位变化逐渐变大,总体在0.5~8 V之间,电位变化曲线如图14所示,可看出由于角度的变化,从0°~90°的电位曲线表现出从两侧峰值一致,到两侧峰值差距逐渐变大,最终只出现一个中心峰值的规律。
图14
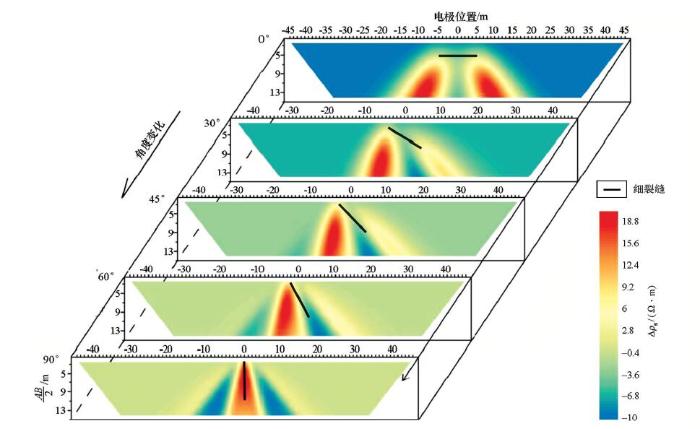
将所得结果进行时移视电阻率成像,分析裂缝隐患在不同倾角下监测异常特征变化。结果如图15所示,可以发现:当裂缝水平放置时,视电阻率显示两个位置对称等大高阻峰值;当角度逐渐变大,两侧高阻峰值位置呈现左高右低的趋势,并且位置不再对称;直到裂缝竖直后,两侧高阻合为一个,出现在裂缝模型的位置处,表现出随隐患形态的变化,异常响应也随之发生形态上改变的特性。
图15
图15
不同倾斜角度细裂缝的视电阻率剖面
Fig.15
Apparent resistivity profile of fine cracks at different tilt angles
4 隐患预警分析
通过上面的模拟结果可以看出,堤坝隐患的类型和尺寸与监测异常的幅值、位置和形态存在密切关系,其中幅值变化更易直观的比较。基于这一特征,本文提出一种堤坝隐患预警机制:通过对异常响应监测结果进行电流归一化处理,提取同种类型的堤坝隐患监测电位峰值,建立异常峰值与隐患尺寸的对应关系,进而根据检测结果快速获得隐患尺寸;然后,根据实际的堤坝结构和隐患尺寸划分灾害等级,进而实现堤坝隐患灾害的快速预警。
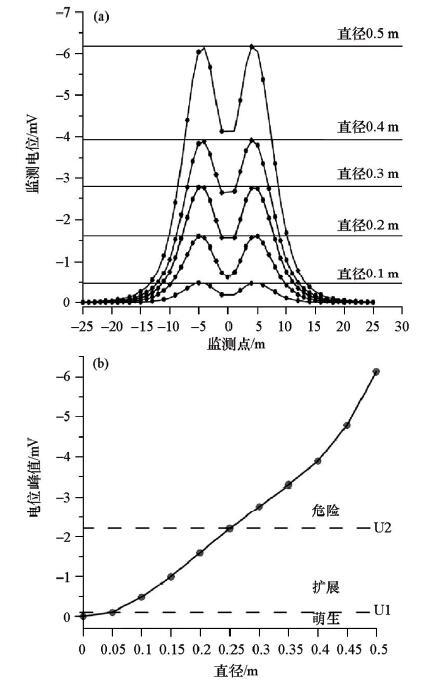
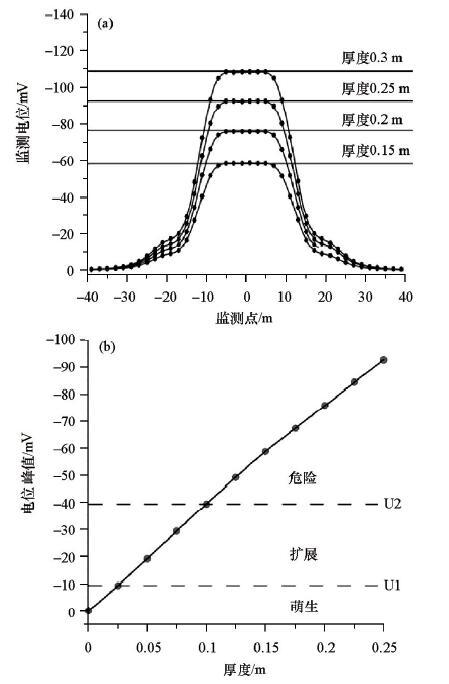
在本文采用的堤坝管漏和层状渗漏模型基础上,计算多种隐患尺度在归一化电流条件下各个监测点上的电位差,如图16a和图17a所示,根据监测曲线上的峰值位置对不同尺度进行划分并提取峰值,将得到的多组数据进行拟合,给出不同尺度与监测峰值的对应关系,如图16b和17b所示。对于同一深度的同类隐患,曲线显示出监测峰值随隐患尺度的增长具有很好的单调性,使得对应关系更加明确。针对此堤坝隐患模型的预警,可以将监测峰值曲线划分为萌生、扩展和危险三个时期(图17b),设定当监测异常信号强度小于U1时为萌生期,异常信号强度大于U1且小于U2时为扩展期,当异常大于U2时为危险期。由无监测异常开始,先进入萌生期,此时河水刚刚侵入,堤坝隐患开始出现,但隐患尺寸较小,导致监测异常信号幅值小;随着时间的推移,在河水冲蚀、基底不均匀沉降等多种原因的作用下,堤坝隐患进入扩展期,此时的监测信号幅值有了明显的增大,表示堤坝内部隐患在不断发展;当监测信号幅值超过U2后将进入危险期,此时堤坝隐患问题非常严重,堤坝处于高度危险的状态。
图16
图16
堤坝管漏监测曲线
a—监测电位曲线;b—电位峰值
Fig.16
Schematic diagram of the dam tube leakage monitoring curve
a— monitoring potential curve;b—peak curve
图17
图17
堤坝层状渗漏监测曲线
a—监测电位曲线;b—电位峰值
Fig.17
Schematic diagram of stratified leakage monitoring curve of dam
a— monitoring potential curve;b—peak curve
本文中U1和U2的选取需要根据具体情况(如堤坝承载力、当地环境特征等因素)进行综合判断确定,本文仅是给出一种分期预警隐患的方式,通过这种方式快速判断隐患对于堤坝安全的影响程度,提前预警堤坝灾害。上述峰值曲线隐患时期的划分,可以作为隐患预警形式的参考。土石堤坝隐患的发展会导致电性异常的多种变化,表现出复杂性。
文中仅是根据监测信号的幅值对堤坝隐患发展趋势做了初步的分析和判断,考虑因素还不够全面。如何通过地表监测信号更加全面地分析堤坝隐患的发展变化趋势,更加准确地给出不同预警时期带的划分依据,将是进一步研究的问题。
5 结语
本文利用非结构三维有限元实现了对堤坝隐患精细正演数值模拟,并得到管状渗漏、层状渗漏,细裂缝三类常见的堤坝隐患模型正演结果,采用时移视电阻率成像方法将正演结果进行处理来模拟对堤坝的实时监测,通过对堤坝隐患三维模型时移成像结果的分析可以得到以下结论:
1) 当堤坝内出现隐患时,采用时移成像可以有效地将隐患的电性特征凸显出来,电势曲线在隐患位置会出现可观测的异常幅度,这表明通过时移方式来实现堤坝隐患实时监测过程是可行的。
2) 对于实际堤坝隐患问题来说,随着河水等自然环境的影响,隐患会逐渐变化。文中对比了不同尺寸和不同埋深、角度的隐患模型的异常响应,结果表明:尺寸、埋深和形态的变化都会在电阻率剖面上得到明显的反应,对于同一类型的隐患尺度越大,埋深越浅,异常变化越显著;隐患所在位置角度的变化也会改变异常峰值出现的位置;对比了三种典型的隐患,结果表明不同形态类型的隐患所产生的异常幅度和形态均有不同。
3) 根据堤坝隐患尺寸与监测电位异常幅度的单调对应关系,可以快速获得隐患尺寸。基于这一结果提出了一种堤坝隐患灾害快速预警机制,可以为堤坝灾害提前预警提供参考。
(本文编辑:沈效群)
参考文献
物探技术在监测堤坝隐患上的应用
[J].<p>对使用地球物理技术监测预报汛期堤防隐患的方法进行了讨论,并介绍了使用分布式高密度电阻率法技术所完成的各种实验结果。</p>
An investigation into the monitoring and forewarning technique for dyke ridden trouble under the condition of high water level
[J].
堤坝隐患无损探测研究应用进展
[J].
Review of non-destructive detection for hidden defects of dams
[J].
高密度电阻率法在珠海某防波堤工程中的应用
[J].高密度电阻率方法在工程勘察中起着越来越重要的作用.本文简明论述了高密度电阻率法的原理、特点.利用本所新购买的由日本生产的MCOHM-21型高密度地电仪,对珠海某防波堤进行了高密度电阻率方法测量,并对测量横剖面利用仪器本身配备的偏移软件进行处理,得到的彩色或灰阶断面图非常直观地反映出防波堤断面的形态分布对纵测线进行分段测量,采用脱机处理数据,给出整个纵测断面等值线图,反应了防波堤长轴方向上抛石的质量情况.文章根据该实测的横剖面和纵剖面的结果评价了利用电测资料估算抛石质量的能力.
The application of the high density resistivity method for the seawave-proof dam in Zhuhai-Harbour
[J].
霍林河水库渗漏探测试验研究
[J].
Experimental study of seepage of Huolin river reservior
[J].
高密度电法在水库大坝塌陷勘测中的应用
[J].
The application of high-density electrical method to the collapse-surveying on the dam
[J].
Resistivity and induced polarization monitoring of salt transport under natural Hydraulic gradients
[J].
Characterization of recharge through complex vadose zone of a granitic aquifer by time-lapse electrical resistivity tomography
[J].
Hydrological response of weathered clay—shale slopes: water infiltration monitoring with time-lapse electrical resistivity tomography
[J].
基于时移高密度电法的覆岩精细探测方法研究
[J].
Fine detection of overburden strata based on time lapse high density resistivity method
[J].
Using resistivity measurements for dam safety evaluation at Enemossen tailings dam in southern Sweden
[J].
Localization and quantification of leakages in dams using time-lapse self-potential measurements associated with salt tracer injection
[J].
基于非结构化网格的瞬变电磁2.5维有限元正演模拟
[J].
Finite element modeling of 2.5D tem using unstructured meshes
[J].
复杂地形三维直流电阻率有限元数值模拟
[J].
DOI:10.3969/j.issn.1004-2903.2009.03.031
Magsci
[本文引用: 1]

<FONT face=Verdana>系统地论述了用有限单元法研究复杂地形条件下三维直流电阻率的正演计算技术.首先给出了三维构造中点源电场的边值问题以及相应的变分问题;然后利用有限单元法求解变分问题,采用四面体单元对研究区域进行剖分,在单元中进行三线性函数插值,将变分方程化为线性代数方程组;最后,考虑到节约计算时间,利用对称超松弛预条件共轭梯度迭代算法求解大型线性方程组,得到了各节点的电位值,进而计算出地表的视电阻率.通过理论模型的计算检验了算法的可行性之后,给出了几种常见纯地形异常的数值模拟结果和一个组合模型的计算结果,其研究工作为研究三维直流电阻率反演奠定了基础.</FONT>
FEM numerical modeling of 3-D DC resistivity under complicated terrain
[J].
三维CSAMT法非结构化网格有限元数值模拟
[J].
Tree-dimensional modeling of controlled-source audio-frequency magnetotellurics using the finite element method on an unstructured grid
[J].
海洋可控源电磁三维非结构矢量有限元数值模拟
[J].
3D Simulation of Marine CSEM Using vector finite element method on unstructured grids
[J].
基于局部加密非结构化网格的三维电阻率法有限元数值模拟
[J].
DOI:10.3969/j.issn.0001-5733.2009.10.023
Magsci
[本文引用: 2]

<FONT face=Verdana>总结了目前常用的结构化网格及其局限性,分析了非结构化网格对复杂地质体边界的适应性和Delaunay三角化算法及其网格加密策略,提出了一种新的局部节点加密方法,实现了对复杂模型的完全非结构化四面体全自动剖分,给出了三维直流电阻率模拟中四面体网格的质量评价标准和最优指标.计算和分析表明,数值解在点电流源及附近的奇异区精度最低,网格加密策略可以有效地减少其影响,极大地提高数值解的精度.本文提出的局部节点加密策略计算量最小,对精度的改善也优于经典方法.在精度要求苛刻或模型十分复杂时,局部体积加密策略和二次单元是高精度模拟的可靠保证.</FONT>
Finite element modeling of 3-D DC resistivity using locally refined unstruetured meshes
[J].
高密度电阻率法及其应用技术研究
[J].
High density measurement method of electrical resistivity and its application technics
[J].