E-mail Alert Rss
 

物探与化探, 2019, 43(3): 618-625 doi: 10.11720/wtyht.2019.1292

方法研究·仪器研制

地震波逆时偏移中两种成像条件应用效果对比

宋宗平1, 陈可洋2, 杨微3, 李来林2, 吴清岭2, 范兴才2

1. 中国石油大庆油田有限责任公司 勘探事业部,黑龙江 大庆 163453

2. 中国石油大庆油田有限责任公司 勘探开发研究院,黑龙江 大庆 163712

3. 中国石油大庆油田有限责任公司 第六采油厂,黑龙江 大庆 163712

Comparison of the application effect of two imaging conditions in seismic wave reverse time migration

SONG Zong-Ping1, CHEN Ke-Yang2, YANG Wei3, LI Lai-Lin2, WU Qing-Ling2, FAN Xing-Cai2

1. PetroChina Exploration Business Department of Daqing Oilfield Co.,Ltd.,Daqing 163453,China

2. PetroChina Exploration and Development Research Institute of Daqing Oilfield Co.,Ltd.,Daqing 163712,China

3. No. 6 Oil Production Company of Daqing Oilfield Co.,Ltd.,Daqing 163712,China

责任编辑: 叶佩

收稿日期: 2018-07-27   修回日期: 2019-04-25   网络出版日期: 2019-06-20

基金资助: 中国石油天然气股份公司重大科技专项“大庆油田原油4000万吨持续稳产关键技术研究”.  2011E-1203

Received: 2018-07-27   Revised: 2019-04-25   Online: 2019-06-20

作者简介 About authors

宋宗平(1963-),男,汉族,博士,高级工程师,主要从事地震勘探技术研究。Email:songzongping@petrochina.com.cn 。

摘要

成像条件是实现地震波场准确成像的关键环节,而优化逆时成像条件在改善逆时成像应用效果中的作用尤为明显。为此,从零井源距和非零井源距脉冲响应出发,系统对比了常规相关法逆时成像条件和基于行波分离法逆时成像条件的逆时偏移脉冲响应波场差异,分析了逆时偏移低波数噪声的成因机理及波场规律,同时以复杂断陷理论模型和SZ工区实际三维地震资料为例,系统对比了两种逆时成像条件的成像应用效果。研究结果表明,采用基于行波分离法逆时成像条件的成像结果能够有效衰减逆时偏移低波数背景噪声,恢复掩盖在这种背景噪声之下的有效地震成像信息,地层细节刻画更加清晰,这可为当前复杂波场和复杂构造高精度地震成像提供方法指导。

关键词： 逆时偏移 ; 成像条件 ; 脉冲响应 ; 理论模型 ; 实际资料 ; 低波数噪声

Abstract

Imaging condition is the key to realizing accurate imaging of seismic wave field,and optimizing reverse-time imaging condition is especially important in improving the application of reverse-time migration method.For this reason,based on the impulse response of zero offset and non-zero offset,this paper compares the reverse-time imaging condition based on one-way wave separation with conventional reverse-time imaging condition in detail.On the basis of the complex theory model and the real 3D seismic data of SZ working area,the imaging effects of two kinds of reverse-time imaging conditions are compared.The results show that the imaging results of the reverse-time imaging condition based on one-way wave separation can effectively attenuate the low wave number background noise,restore the effective seismic imaging information concealed under this background noise,and the stratigraphic details are characterized more clearly.These results can provide guidance for the high precision seismic imaging of complex wave fields and complex structures.

Keywords： reverse-time migration ; imaging condition ; impulse response ; model study ; seismic data ; low wave number noise

PDF (5099KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

宋宗平, 陈可洋, 杨微, 李来林, 吴清岭, 范兴才. 地震波逆时偏移中两种成像条件应用效果对比. 物探与化探[J], 2019, 43(3): 618-625 doi:10.11720/wtyht.2019.1292

SONG Zong-Ping, CHEN Ke-Yang, YANG Wei, LI Lai-Lin, WU Qing-Ling, FAN Xing-Cai. Comparison of the application effect of two imaging conditions in seismic wave reverse time migration. Geophysical and Geochemical Exploration[J], 2019, 43(3): 618-625 doi:10.11720/wtyht.2019.1292

0 引言

地震波逆时成像技术是当前高精度复杂波场复杂构造成像的关键技术之一,其具体成像过程包括震源波场的正向传播和检波点波场的逆时延拓,这两个步骤完全可以借鉴地震波正演模拟相关数值理论算法,能够保证逆时偏移计算过程稳定和满足计算精确等的要求。与地震波正演模拟差异之处在于,逆时成像技术需要在地下任意成像空间位置应用逆时成像条件实现地震波场的准确归位[1,2,3,4],与其他深度域地震成像技术不同,其具有以下诸多优点[5,6,7,8,9]:①采用全地震波动方程实现全波场成像,因此对波动方程的近似最少;②能够解决多次波等多路径、多值走时等的复杂波场成像问题;③适合于速度较为剧烈变化和陡倾角等的复杂构造成像问题。

随着近些年GPU高性能计算技术和大容量并行存储技术等的飞速发展[10],有效缓解了海量存储和巨大计算量的技术瓶颈,推进了实际地震资料逆时成像技术的工业化应用进程,并取得了丰富的理论成果和应用成果[11,12,13,14,15,16,17,18],包括适合逆时偏移的叠前保真地震资料处理、高精度速度建模(如层析速度建模、全波形反演建模等)、高精度逆时成像技术(如基于声学介质、各向异性/各向同性弹性介质等[19])等。逆时成像技术的算法精度得益于地震波动力学相关数值计算方法的创新研究,如地震波动方程的近似离散化问题[11](如有限差分法、有限元法、伪谱法等)、人为截断边界的边界吸收问题[20,21,22,23](如完全匹配层吸收边界、阻尼吸收边界等)、计算稳定性问题、数值频散压制问题等,也得益于基于逆时成像技术特点的相关技术创新研究,例如逆时成像条件的改进与优化问题[24,25,26](如相关法成像条件、震源归一化成像套件、时空移成像条件等)、逆时背景噪声压制问题[27,28,29,30](如拉普拉斯去噪、波场分离成像条件等)。因此,逆时成像技术已在滨里海、墨西哥湾、北海等地区的盐下或盐丘侧翼等海洋地震资料的应用中取得了重大突破,同时在高陡构造成像、复杂山前带成像、起伏地表成像、碳酸盐岩缝洞成像等陆地地震资料应用中也已取得了较为丰富的研究成果[31,32,33,34]。

在前人研究的基础上,从脉冲响应、理论模型和实际资料三个方面出发,系统对比了常规相关法逆时成像条件和基于行波分离法逆时成像条件这两种逆时成像条件的波场特征差异及应用效果,其结果可为复杂油气勘探目标高精度地震成像提供理论指导和技术支撑。

1 基本原理

以各向同性介质地震波动方程为例进行逆时偏移研究,其公式如下:

∂2P∂t2=V2∂2P∂x2+∂2P∂y2+∂2P∂z2,

式(1)中:P代表地震波场;V代表地球介质速度;t代表时间;x,y,z代表空间坐标。

逆时成像技术包含震源波场正向传播、检波点波场逆时延拓、应用成像条件共3个步骤,其中前两者的公式依次为:

Pn+1=2Pn-Pn-1+Q+fsource(x0,y0,z0,t),
Pn-1=2Pn-Pn+1+Q+frecord(x1,y1,z1,t)。

式(2)和式(3)中:x0,y0,z0代表某一震源的空间坐标;x1,y1,z1代表某一检波器的空间坐标;t代表时间;n=0,1,2,…,N;N代表总接收道长的总采样点个数;Pn+1,Pn,Pn-1分别为下一时刻、当前时刻和上一时刻的波场值;fsource代表震源波场函数;frecord代表检波器接收的地震记录。笔者采用时间2阶、空间16阶精度的有限差分方法对式(1)进行数值离散化,人工截断边界处采用10个网格点的完全匹配层(PML)吸收边界条件,可确保逆时偏移处理具有较高的数值精度和可靠性[10]。

逆时成像条件是实现地震波场准确成像的关键环节,工业界普遍采用常规相关法逆时成像条件,对于任意一炮数据的逆时成像条件计算公式如下:

Image1=∫tPs·Pr=<∫tPs,up·Pr,up+∫tPs,up·Pr,down+∫tPs,down·Pr,up+∫tPs,down·Pr,down>,

式(4)中,Ps和Pr分别代表炮点波场和检波点波场,下标up和down分别代表上行波和下行波这两种波场。分析式(4)可知,常规的震源波场和检波点波场的互相关计算可以进一步分解为炮点波场(上行波和下行波)和检波点波场(上行波和下行波)的两两互相关计算,共由4个部分波场相关成像组成。为了在成像过程中压制低波数逆时偏移背景噪声,引入基于行波分离法逆时成像条件[26,27],对于任意一炮数据的逆时成像条件计算公式如下:

Image2=∫tPs,up·Pr,up+∫tPs,down·Pr,down。

分析式(5)可知,基于行波分离法逆时成像条件只保留了式(4)中的2项,模型研究表明,不同传播方向的震源波场和检波点波场的互相关计算是形成逆时偏移低波数背景噪声的主要成因,相同传播方向的震源波场和检波点波场的互相关计算能够有效提高成像精度和信噪比。因此,笔者采用脉冲响应、理论模型和实际地震资料,系统对比了常规相关法逆时成像条件和基于行波分离法逆时成像条件的逆时偏移应用效果。

2 脉冲响应研究

脉冲响应是验证地震成像准确性的一种有效方法,也是指导实际地震资料逆时偏移处理的一种重要手段[32]。这里以三层各向同性层状介质速度模型为例,对比了常规相关法逆时成像条件和基于行波分离法逆时成像条件的脉冲响应。

模型尺寸为1 km×1 km,空间步长为5 m×5 m,第一层速度为2 000 m/s,第二层速度为3 000 m/s,第三层速度为4 000 m/s。零偏移距逆时偏移脉冲响应情况,在模型地表中间位置布置1个震源和1个检波器,如图1a所示;有偏移距逆时偏移脉冲响应情况,震源和检波器均布置于地表位置,炮检点间距为300 m,如图2a所示。震源采用峰值频率为40 Hz的雷克子波,检波点波场采用含5个不同幅值和相位的褶积记录。

图1

新窗口打开| 下载原图ZIP| 生成PPT

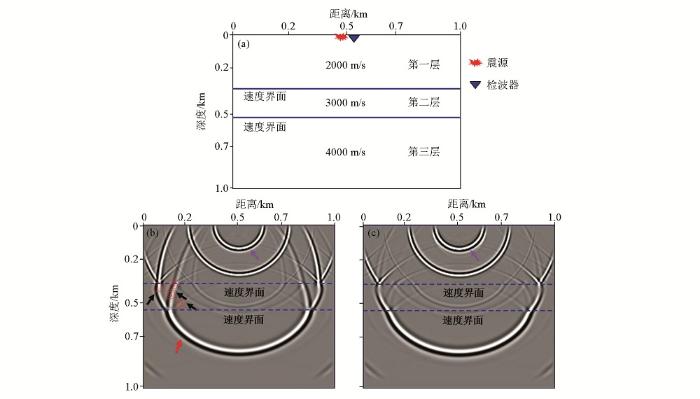
图1   2种逆时成像条件零偏移距脉冲响应对比

a—层状介质模型零偏移距观测系统;b—采用常规逆时成像条件对应的脉冲响应;c—采用基于行波分离法逆时成像条件对应的脉冲响应

Fig.1   Comparison of zero offset reverse-time migration impulses between two different imaging conditions

a—Zero offset survey with layered medium model;b—Impulse response with conventional reverse-time;c—Impulse response with reverse-time migration condition based on one-way wave separation


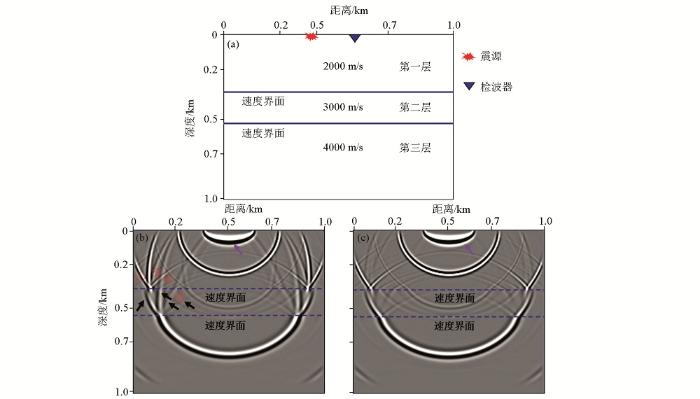
在第一层介质中,零偏移距逆时偏移脉冲响应波场呈圆形(图1b和图1c中紫色箭头所示),有偏移距逆时偏移脉冲响应波场呈椭圆形(图2b和图2c中紫色箭头所示)。随着脉冲响应与层状介质速度界面的相互作用(反射和透射等),速度大的一侧,脉冲响应波场传播的更远,同时有偏移距逆时偏移脉冲响应在速度界面上方形成4条脉冲响应曲线(图2b中黑色箭头所示),而零偏移距逆时偏移脉冲响应是有偏移距逆时偏移脉冲响应的特例,即震源和检波点位置重叠,其在速度界面上方形成3条脉冲响应曲线(图1b中黑色箭头所示)。根据逆时偏移脉冲响应机理[32],图2b中的4条脉冲响应曲线分别为:由以震源位置和检波点位置为焦点的脉冲响应椭圆曲线(①);以震源位置在速度界面的投影和检波点位置在速度界面的投影为焦点的脉冲响应椭圆曲线(②);以检波点位置在速度界面的投影和震源位置为焦点的脉冲响应椭圆曲线(③);以震源位置在速度界面的投影和检波点位置为焦点的脉冲响应椭圆曲线(④)。其中曲线①和②代表式(5)对应的逆时成像脉冲响应曲线,是同方向震源波场和检波点波场的互相关计算结果,曲线③和④是不同方向震源波场和检波点波场的互相关计算结果,且在零偏移距逆时偏移脉冲响应情况两条曲线重叠,因此是形成逆时偏移低波数背景噪声的主要贡献波场。对比图1b、1c和图2b、2c可知,应用基于行波分离法逆时成像条件后,曲线③和④对应的脉冲响应波场得到了明显压制。对于任一炮地震数据的逆时偏移结果,是由N个检波点波场与1个震源波场组成的N个有偏移距脉冲响应波场叠加而成,因此通过这种叠加处理能够进一步提高逆时偏移结果的成像精度和信噪比。分析还可知,逆时偏移脉冲响应中无明显数值频散现象,人工截断边界处边界反射能量较弱,由此表明,笔者采用的逆时偏移算法具有较高数值计算精度,成像结果可靠,可以满足实际地震资料高精度逆时成像的应用需求。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   2种逆时成像条件有偏移距逆时偏移脉冲响应对比

a—层状介质模型有偏移距观测系统;b—采用常规逆时成像条件对应的脉冲响应;c—采用基于行波分离法逆时成像条件对应的脉冲响应

Fig.2   Comparison of offset reverse-time migration impulse between two different imaging conditions

a—Zero offset survey with layered medium model;b—Impulse response with conventional reverse-time;c—Impulse response with reverse-time migration condition based on one-way wave separation


3 理论模型研究

为了验证第1小节逆时偏移脉冲响应分析得出的结论,这里参考大庆探区某地区复杂断陷盆地特点建立了理论模型(图3a)。模型总大小为45 km×4.5 km,空间步长为5 m×5 m,模型最小速度为1 700 m/s,最大速度为5 100 m/s,采用峰值频率为30 Hz的雷克子波进行正演模拟和逆时成像,数据采样率为1 ms, 接收道长为4 s。采用双边观测方式,共371炮,每炮801道接收,最小偏移距为0 km,最大偏移距为4 km。对采集的单炮记录分别应用常规相关法逆时成像条件和基于行波分离法逆时成像条件进行应用效果对比分析。

图3

新窗口打开| 下载原图ZIP| 生成PPT

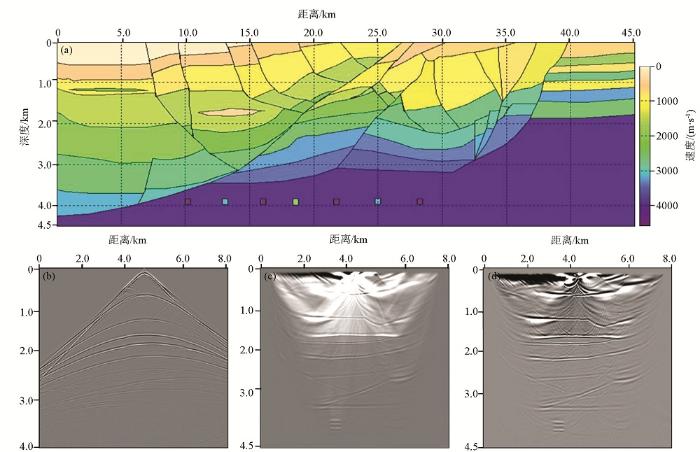
图3   不同逆时成像条件理论模型单炮逆时偏移结果

a—复杂构造速度模型;b—正演模拟单炮记录;c—常规逆时成像条件单炮偏移结果;d—基于行波分离法逆时成像条件单炮偏移结果

Fig.3   One shot theoretical model reverse-time migration result with different imaging condition

a—Complex velocity model;b—Forward simulation shot gather record;c—Migration result of one shot gather with conventional reverse-time imaging condition;d—Migration result of one shot gather with reverse-time imaging condition based on one-way wave separation scheme


图3b为图3a震源位置处激发的波动方程正演模拟记录。分析可知,单炮记录无明显的数值頻散现象,同时边界反射能量较弱,由此表明文中采用的高阶有限差分算法及PML边界条件具有较高的数值模拟精度。图3c和图3d分别为应用常规相关法逆时成像条件和基于行波分离法逆时成像条件后的理论模型单炮逆时偏移结果,图4a和图4b分别为应用常规相关法逆时成像条件和基于行波分离法逆时成像条件后的理论模型逆时偏移叠加结果。对比可知,应用常规逆时成像条件的成像结果存在较强能量的低波数背景噪声,几乎掩盖了有效反射地层信息,地层越浅,背景噪声越强,同时背景噪声从浅层到深层逐渐减弱,具有一定的成层性,即波阻抗越大,其上方的低波数背景噪声能量就越强,反之亦然。而应用基于行波分离法逆时成像条件后的成像结果中,这种背景噪声得到了有效衰减,恢复出了掩盖在强能量背景噪声之下的有效反射信号,地层接触关系清晰准确,具有更高的信噪比和成像精度。通过分析还可知,这种逆时偏移背景噪声的成因与第1小节逆时偏移脉冲响应分析中削弱的2条脉冲响应椭圆曲线有密切相关性,由此表明基于行波分离法逆时成像条件具有更高的成像精度和信噪比。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同逆时成像条件理论模型逆时偏移叠加结果

a—常规逆时成像条件偏移叠加结果;b—基于行波分离法逆时成像条件偏移叠加结果

Fig.4   Theoretical model reverse-time migration result with different imaging condition

a—Migration result with conventional reverse-time imaging condition;b—Migration result with reverse-time imaging condition based on one-way wave separation scheme


4 实际工区应用

以松辽盆地SZ工区为例,其近地表条件较为简单,高分辨率、高精度地震成像是该区处理的难点。该工区采用基于构造约束的网格层析速度建模方法建立深度域速度模型,同时采用适合逆时偏移的地震资料预处理技术得到高保真的共炮点道集。该工区成像面元为25 m×25 m,深度域速度模型中最小速度为1 851 m/s,最大速度为6 534 m/s,根据数值頻散关系[7]和输入数据频谱分析,优选逆时偏移最大偏移频率为66 Hz,分别应用常规相关法逆时成像条件和基于行波分离法逆时成像条件进行高精度逆时成像处理,并应用CPU/GPU协同高性能集群并行计算技术加速逆时偏移处理[10],缩短处理周期。

图5a和图5b分别为实际地震资料应用常规相关法逆时成像条件和基于行波分离法逆时成像条件后的逆时偏移叠加结果(在相同数值范围显示对比,仅成像条件的差异)。分析图5a可知,由于逆时偏移低波数背景噪声的存在,地层细节成像不清楚,掩盖了有效的地层反射信号,而应用基于行波分离法逆时成像条件后(图5b),成像结果中的地层细节刻画更加清楚、能量一致性更好,同时波数谱中低波数能量得到了有效压制,波数谱带宽得到展宽,由此验证了基于行波分离法逆时成像条件具有更高的成像精度,能够在逆时成像过程中有效压制低波数背景噪声,恢复有效地震反射细节,提高成像分辨率和信噪比。

图5

新窗口打开| 下载原图ZIP| 生成PPT

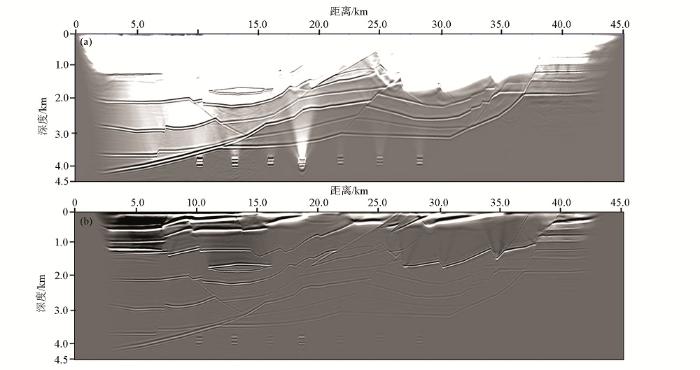
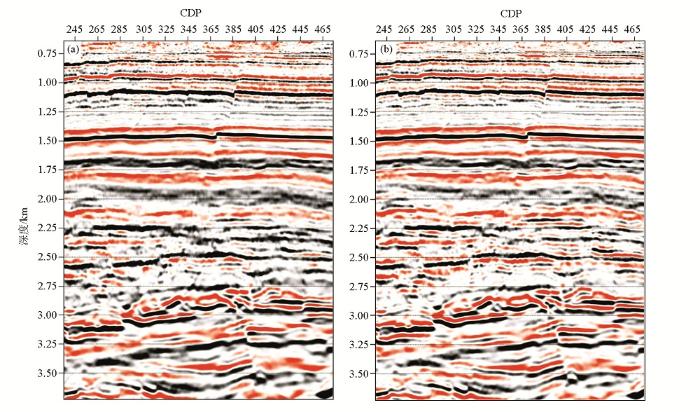
图5   松辽盆地SZ工区不同逆时成像条件实际资料逆时偏移结果对比

a—常规逆时成像条件偏移叠加结果;b—基于行波分离法逆时成像条件偏移叠加结果

Fig.5   Practical data reverse-time migration result with different imaging condition in SZ area of Songliao Basin

a—Migration result with conventional reverse-time;b—Migration result with reverse-time imgaing condition based on one-way wave separation scheme


5 结论

文中从成像机理、脉冲响应、理论模型和实际地震资料4个方面系统对比了常规相关法逆时成像条件和基于行波分离法逆时成像条件这2种逆时成像条件及其应用效果,得出如下结论:

1)在均匀层状介质中,零偏移距和有偏移距脉冲响应波场分别呈现圆形和椭圆形,且只形成1条脉冲响应曲线,曲线的焦点为其震源位置和检波点位置;

2)在速度差异界面上方,有偏移距逆时偏移脉冲响应共形成4条脉冲响应曲线,曲线的焦点为其震源位置和检波点位置及其在速度界面的投影。其中零偏移距逆时偏移脉冲响应是其在震源和检波点位置重叠时的特例,使得有2条脉冲响应曲线相互重叠,只形成3条脉冲响应曲线。

3)不同传播方向的震源波场和检波点波场的互相关计算是形成逆时偏移低波数背景噪声的主要成因,基于行波分离法逆时成像条件将其进行了有效压制,通过保留相同传播方向的震源波场和检波点波场的互相关计算显著提高成像结果的精度和信噪比。

4)低波数背景噪声具有浅层能量强、深层能量弱,同时存在一定的成层性,地层界面的波阻抗差异越大,其上方的低波数背景噪声能量就越强,掩盖了有效地震反射信息,反之亦然,复杂构造理论模型及SZ地区实际地震资料逆时成像应用效果验证了该结论。

The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。

参考文献

陈可洋 .

高阶弹性波波动方程正演模拟及逆时偏移成像研究

[D]. 大庆:大庆石油学院, 2009.

[本文引用: 1]

Chen K Y .

High-order elastic wave equation forward modeling and reverse-time migration

[D]. Daqing:Daqing Petroleum Institute, 2009.

[本文引用: 1]

Claerbout J F .

Imaging the Earth’s Interior

[D].Palo Alto: Blackwell Scientific Publications Inc., 1985.

[本文引用: 1]

Baysal E, Kosloff D D , Sherwood J W C.

Reverse time migration

[J]. Geophysics, 1983,48(11):1514-1524.

DOI:10.1190/1.1441434      URL     [本文引用: 1]

陈可洋 .

基于高阶有限差分的波动方程叠前逆时偏移方法

[J]. 石油物探, 2009,48(5):475-478.

[本文引用: 1]

Chen K Y .

Wave equation pre-stack reverse-time migration scheme based on high-order finite-difference

[J]. Geophysical Prospecting For Petroleum, 2009,48(5):475-478.

[本文引用: 1]

Liu G, Liu Y, Li R , et al.

3D seismic reverse time migration on GPGPU

[J]. Computers & Geosciences, 2013a,59:17-23.

[本文引用: 1]

康玮, 程玖兵 .

叠前逆时偏移假象去除方法

[J]. 地球物理学进展, 2012,27(3):1163-1172.

DOI:10.6038/j.issn.1004-2903.2012.03.041      Magsci     [本文引用: 1]

叠前逆时偏移(RTM)求解全波动方程进行波场延拓,可以精确描述地震波的传播,在陡倾界面和复杂构造成像方面具有显著优势.但在实际应用中,互相关成像条件会带来低波数高振幅的假象.本文分析了假象产生的原因,实现并比较了Laplace滤波、坡印廷矢量法和上下、左右行波分解这三种假象压制方法,针对不同的计算平台分析其优劣.数值试验表明,坡印廷矢量法当波场简单时较为有效;而上下、左右行波分解法和Laplace滤波可以应对较复杂的波场.就去假象结果而言,使用波场分解成像条件并施加Laplace滤波效果最佳;然而就计算效率而言,CPU平台应用波场分解成像条件只增加少量的计算量,但GPU平台的实现则需要对数据的读写付出较大的代价.因此,综合考虑,对于CPU平台上述两种方案的组合为最佳策略;而基于GPU平台的逆时偏移采用Laplace滤波去噪仍然是目前最经济的选择.Marmousi模型和SEG/HESS VTI模型试验验证了上述结论.

Kang W, Cheng J B .

Methods of suppressing artifacts in prestack reverse time migration

[J]. Progress in Geophysics, 2012,27(3):1163-1172.

Magsci     [本文引用: 1]

Chen K .

Anisotropic analysis of difference approximation in seismic wave numerical modeling

[J]. Geophysical Prospecting For Petroleum, 2010,49(1):19-22.

[本文引用: 2]

杨仁虎, 常旭, 刘伊克 .

叠前逆时偏移影响因素分析

[J]. 地球物理学报, 2010,53(8):1902-1913.

DOI:10.3969/j.issn.0001-5733.2010.08.016      Magsci     [本文引用: 1]

反射地震勘探中的偏移成像技术是获取地下介质构造形态最有效的手段之一.在叠前深度域偏移方法中,目前工业界采用的方法包括基于射线理论的波动方程积分解法和基于波动理论的微分波动方程单程波解法,这两类方法难以处理地震波横向速度变化剧烈的高陡倾角构造成像问题.近年来勘探地震学研究领域发展起来的叠前逆时偏移采用了双程波求解微分波动方程的算法,这种方法具有相位准确、不受介质横向速度变化和高陡倾角构造的影响、成像精度高、可以利用回转波正确成像等优点,从理论上弥补了当前工业界常规地震偏移所面临的成像缺陷.然而,叠前逆时偏移成像方法从理论走向实用尚需解决如下问题:计算速度和数据存储空间的节省、初始速度模型的建立、震源子波的选择、数值模型边界条件的定义和假像的消除等等.对于计算速度和存储量大的问题,随着计算机硬件的快速发展,将会不断得到改善,同时可以采取一些计算技术和存储策略来加以缓解.本文主要针对初始速度模型的建立、震源子波的选择、数值模型边界条件的定义和假像的消除这些因素,利用简单模型进行了分析.对于反射波造成的传播路径上的假像,给出了一种振幅补偿滤波方法.对勘探地球物理学界给出的SEG/EAGE二维盐丘模型、Marmousi模型和本研究设计的崎岖海底模型进行了叠前逆时偏移成像,均取得了较好的成像效果.

Yang R H, Chang X, Liu Y K .

The influence factors analyses of imaging precision in pre-stack reverse time migration

[J]. Chinese Journal of Geophysics, 2010,53(8):1902-1913.

Magsci     [本文引用: 1]

Chang W , McMechan G A.

3D acoustic prestack reverse-time migration

[J]. Geophysical Prospecting, 1990,38(7):737-756.

DOI:10.1111/gpr.1990.38.issue-7      URL     [本文引用: 1]

陈可洋 .

逆时成像技术在大庆探区复杂构造成像中的应用

[J]. 岩性油气藏, 2017,29(6):91-100.

[本文引用: 3]

Chen K Y .

Reverse-time migration technology for complex structure imaging of Daqing exploration area

[J]. Lithologic Reservoirs, 2017,29(6):91-100.

[本文引用: 3]

Wang Y, Liang W, Nashed Z , et al.

Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship preserving method

[J]. Geophysics, 2014,79:T277-T285.

DOI:10.1190/geo2014-0078.1      URL     [本文引用: 2]

Zhang H, Zhang Y.

Reverse time migration in 3D heterogeneous TTI media

[C]//SEG Technical Program Expanded Abstracts, 2008: 2196-2200.

[本文引用: 1]

Zhao Y, Liu Y, Ren Z .

Visco acoustic prestack reverse time migration based on the optimal time-space domain high-order finite difference method

[J]. Applied Geophysics, 2014,11(1):50-62.

DOI:10.1007/s11770-014-0414-8      URL     [本文引用: 1]

Xu S, Zhang Y, Tang B .

3D angle gathers from reverse time migration

[J]. Geophysics, 2011,76(2):S77-S92.

DOI:10.1190/1.3536527      URL     [本文引用: 1]

王保利, 高静怀, 陈文超 , 等.

逆时偏移中用Poynting矢量高效地提取角道集

[J]. 地球物理学报, 2013,56(1):262-268.

DOI:10.6038/cjg20130127      Magsci     [本文引用: 1]

<p>逆时偏移在提高复杂介质的成像质量方面表现出了优越的性能,但逆时偏移对速度精度的要求比较高.共成像点道集是一种非常重要的叠前深度偏移输出,它除了能为深度偏移处理提供速度信息外,还能够提供振幅和相位等信息,为后续的属性解释提供依据.本文提出一种在逆时偏移成像过程中提取角度域共成像点道集的方法,该方法采用矢量波动方程进行波场传播,并用能流密度矢量(Poynting vector)计算反射角,最后应用互相关成像条件输出角度域共成像点道集.该方法简单易于实现,且几乎不需要额外的计算量和存储量,非常适合于进行逆时偏移速度分析,同时提出的角道集也能用于进行AVA等分析.最后通过模型算例和实际数据检验了方法的有效性和优越性.</p>

Wang B L, Gao J H, Chen W C , et al.

Extracting efficiently angle gathers using Poynting vector during reverse time migration

[J]. Chinese Journal of Geophysics, 2013,56(1):262-268.

Magsci     [本文引用: 1]

Zhang J, Yao Z .

Optimized finite difference operator for broadband seismic wave modeling

[J]. Geophysics, 2013,78:A13-A18.

DOI:10.1190/geo2012-0277.1      URL     [本文引用: 1]

许璐, 孟小红, 刘国峰 .

逆时偏移去噪方法研究进展

[J]. 地球物理学进展, 2012,27(4):1548-1556.

[本文引用: 1]

Xu L, Meng X H, Liu G F .

Reverse time migration and removing artifacts

[J]. Progress in Geophysics, 2012,27(4):1548-1556.

[本文引用: 1]

陈可洋 .

松辽盆地地震资料小面元叠前插值逆时偏移处理

[J]. 油气藏评价与开发, 2015,5(4):12-16.

[本文引用: 1]

Chen K Y .

Seismic data small bin pre-stack reverse-time migration processing in Songliao Basin

[J]. Reservoir Evaluation and Development, 2015,5(4):12-16.

[本文引用: 1]

Chen K, Chen S, Li L , et al.

Numerical experiments on the elastic wave united pre-stack reverse-time migration

[J]. Geophysical Prospecting for Petroleum, 2014,53(1):8-16.

[本文引用: 1]

Chen K .

Study on perfectly matched layer absorbing boundary condition

[J]. Geophysical Prospecting for Petroleum, 2010,49(5):472-477.

[本文引用: 1]

Chen K .

Evaluation on the bordering method of the absorbing boundary condition

[J]. Journal of the Graduate School of the Chinese Academy of Sciences, 2010,27(2):170-175.

[本文引用: 1]

Wang B, Chen J, Chen W .

Efficient boundary storage strategies for seismic reverse time migration

[J]. Chinese Journal of Geophysics, 2012,55(7):2412-2421.

[本文引用: 1]

Chen K, Fan X, Wu Q , et al.

Improvement of reverse-time migration precision with seismic wave pre-stack interpolation processing and application

[J]. Geophysical Prospecting for Petroleum, 2013,52(4):409-416.

[本文引用: 1]

王娟, 李振春, 陶丽 .

逆时偏移成像条件研究

[J]. 地球物理学进展, 2012,27(3):1173-1182.

DOI:10.6038/j.issn.1004-2903.2012.03.042      Magsci     [本文引用: 1]

本世纪初高性能计算技术进步促进了逆时偏移技术的应用与发展.为解决逆时偏移存在的低频噪音等问题,可利用优化的角度域成像条件对成像进行改进;为实现真振幅逆时偏移,选择合适的成像条件也至关重要.根据不同的成像目的,有必要对逆时偏移使用的成像条件进行深入的分析.本文给出了逆时偏移的五类成像条件,并主要从噪音与振幅等方面对各种方法分别进行了分析说明,为逆时偏移的进一步应用提供方法对比.

Wang J, Li Z C, Tao L .

The research on imaging condition of reverse time migration

[J]. Progress in Geophysics, 2012,27(3):1173-1182.

Magsci     [本文引用: 1]

Chen K .

Time-limited time-shift correlation pre-stack reverse-time image condition and its application

[J]. Geophysical Prospecting For Petroleum, 2010,50(1):22-26.

[本文引用: 1]

陈可洋 .

基于波场分离和角度域衰减的地震波叠前逆时成像条件

[J]. 计算物理, 2016,33(2):205-211.

[本文引用: 2]

Chen K Y .

Seismic wave pre-stack reverse-time migration imaging condition based on one-way wave field separation and angle domain attenuation

[J]. Chinese Journal of Computational Physics, 2016,33(2):205-211.

[本文引用: 2]

徐兴荣, 王西文, 王宇超 , 等.

基于波场分离理论的逆时偏移成像条件研究及应用

[J]. 地球物理学进展, 2012,27(5):2084-2090.

[本文引用: 2]

Xu X R, Wang X W, Wang Y C , et al.

Study and application of imaging condition for reverse-time migration based on wave-fields separation

[J]. Progress in Geophysics, 2012,27(5):2084-2090.

[本文引用: 2]

陈康, 吴国忱 .

逆时偏移拉普拉斯算子滤波改进算法

[J]. 石油地球物理勘探, 2012,47(2):249-255.

DOI:      Magsci     [本文引用: 1]

本文在分析拉普拉斯滤波方法的基本原理及其存在问题的基础上，提出了四阶拉普拉斯滤波算法，有效地解决了逆时偏移去噪中遇到的压制噪声不彻底及子波振幅和相位发生明显变化的问题，也就是说,此法可以在更好地消除成像噪声的同时，保持有效信号的振幅和相位特性。简单和复杂模型数据的测试表明，改进的拉普拉斯算子滤波算法效果明显。

Chen K, Wu G C .

An improved filter algorithm based on Laplace operator in reverse-time migration

[J]. Oil Geophysical Prospecting, 2012,47(2):249-255.

Magsci     [本文引用: 1]

丁亮, 刘洋 .

逆时偏移成像技术研究进展

[J]. 地球物理学进展, 2011,26(3):1085-1100.

DOI:10.3969/j.issn.1004-2903.2011.03.039      Magsci     [本文引用: 1]

近年来,基于双程波动方程的逆时偏移方法在地震成像领域吸引了越来越多地球物理学家的关注.逆时偏移方法相对于实际油气勘探过程中被广泛应用的Kirchhoff偏移方法和单程波波动方程偏移方法,具有原理简单、成像精确且无倾角限制、适应任意复杂速度模型等诸多优点.本文首先概述了逆时偏移近三十年的发展历程,然后重点介绍了逆时偏移方法的主要新进展,内容包括波动方程数值解法的改进、成像条件的相对保幅性分析、低频噪音的消除、多波多分量逆时偏移方法、各向异性逆时偏移方法以及计算效率的提高等方面.最后对逆时偏移方法的应用现状进行了总结,并预测了逆时偏移未来的发展趋势和研究重点.

Ding L, Liu Y .

Progress in reverse time migration imaging

[J]. Progress in Geophysics, 2011,26(5):1085-1100.

Magsci     [本文引用: 1]

Di Bartolo L, Dors C, Mansur W J .

A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation

[J]. Geophysics, 2012,77:T187-T199.

DOI:10.1190/geo2011-0345.1      URL     [本文引用: 1]

Liu S, Wang H, Chen S , et al.

Implementation strategy of 3D reverse time migration on GPU/CPU clusters

[J]. Chinese Journal of Geophysics, 2013b,56(10):3487-3496.

[本文引用: 1]

Chen K, Wu Q, Fan X , et al.

Study on seismic wave pre-stack reverse-time migration’s impulse response and its application

[J]. Geophysical Prospecting For Petroleum, 2013,52(2):163-170.

[本文引用: 3]

Symes W W.

Reverse time migration with optimal check pointing

[J].Geophysics, 2007, 72:SM213-SM221.

DOI:10.1190/1.2742686      URL     [本文引用: 1]

陈可洋 .

地震波逆时偏移方法研究综述

[J]. 勘探地球物理进展, 2010,33(3):153-159.

[本文引用: 1]

Chen K Y .

Reviews on seismic wave reverse-time migration methods

[J]. Progress in Exploration Geophysics, 2010,33(3):153-159.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com