E-mail Alert Rss
 

物探与化探, 2019, 43(2): 359-366 doi: 10.11720/wtyht.2019.1261

方法研究·信息处理·仪器研制

LSQR法在位场反演中的分析与评价

梁生贤, 王桥, 焦彦杰, 廖国忠, 郭境

中国地质调查局 成都地质调查中心,四川 成都 610081

Analysis and evaluation of the potential field inversion using LSQR method

LIANG Sheng-Xian, Wang Qiao, JIAO Yan-Jie, LIAO Guo-Zhong, GUO Jing

Chengdu Center, China Geological Survey, Chengdu 610081, China

责任编辑: 王萌

收稿日期: 2018-07-2   修回日期: 2019-01-16   网络出版日期: 2019-04-20

基金资助: 国家重点研发计划项目.  2016YFC060308,2018YFC0604103

Received: 2018-07-2   Revised: 2019-01-16   Online: 2019-04-20

作者简介 About authors

梁生贤(1984-),男,工程师,主要从事重、磁、电勘探与研究工作。Email:liangshengxian626@163.com 。

摘要

LSQR法具有计算效率高、对计算机内存要求低的优点,适合于大规模问题的求解。为探讨其应用于位场反演的稳定性和可靠性,笔者以加入不同噪声的两个合成模型数据为实验对象,比较分析了Tikhonov正则化与LSQR法求解结果,显示直接利用LSQR法求解位场反问题能够得到满意的正则化解,其解模型相对Tikhonov正则化,最大相对误差仅为0.36%,说明直接利用LSQR法求解位场反问题是可行的。将其应用于四川盆地雅安地区重力三维反演,极大地降低计算成本,获取了区内沉积盆及主要断裂分布情况,为页岩气靶区优选提供了有力支撑。

关键词： 迭代正则化 ; LSQR法 ; Tikhonov正则化 ; 位场反演

Abstract

The LSQR method has the advantages of high computing efficiency and low memory requirement, and is thus suitable for solving large-scale ill-posed problems. In order to discuss its application in the stability and reliability of potential field inversion, the authors, on the basis of two synthetic models data with different noises as the object of the experiment, studied Tikhonov regularization and LSQR method, and the results show that the LSQR method can satisfy the requirement for solving potential field inversion with the regularization solution. In comparison with Tikhonov regularization, the maximum relative error of the LSQR method is only 0.36%, indicating that the use of LSQR method to solve potential field inverse problems is feasible. It was applied to 3D inversion of gravity in Ya’an area of Sichuan basin, which greatly reduced computation cost and obtained the distribution of sedimentary basins and main faults in the area, thus providing strong support for shale gas target area optimization.

Keywords： iterative regularization ; LSQR method ; Tikhonov regularization ; potential field inversion

PDF (2726KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

梁生贤, 王桥, 焦彦杰, 廖国忠, 郭境. LSQR法在位场反演中的分析与评价. 物探与化探[J], 2019, 43(2): 359-366 doi:10.11720/wtyht.2019.1261

LIANG Sheng-Xian, Wang Qiao, JIAO Yan-Jie, LIAO Guo-Zhong, GUO Jing. Analysis and evaluation of the potential field inversion using LSQR method. Geophysical and Geochemical Exploration[J], 2019, 43(2): 359-366 doi:10.11720/wtyht.2019.1261

0 引言

位场反演是根据位场(重力场或磁场)的空间分布特征来确定对应的场源体特征[1],是资料定量解释的重要环节之一。其中物性反演将模型空间离散化为若干个单元,只求解各单元相应的密度或磁性 [1-2],可归结为离散不适定问题,需要特殊的求解方法,即正则化方法。

不适定问题的正则化方法可分为直接正则化(如:Tikhonov和TSVD)与迭代正则化(如:CGLS、LSQR),尽管其在理论上已较为完善,但对同一问题不同算法可能表现出相似或不同的收敛性质 [3-6],其计算成本也存在差异。在位场以及电法资料反演中,应用最为广泛的为Tikhonov正则化。直接法(SVD)求解大型问题虽然稳定可靠但计算成本较高,LSQR与CGLS法越来越多地被应用于求解线性方程组 [7-11]。此外,对于Tikhonov正则化,每反演迭代一次都需通过多次计算选择最佳正则化参数,无疑增加了计算成本。

若直接利用迭代法如LSQR法求解位场反问题,由于其具有天然的正则化性质和降维的特点,将极大地节省计算成本。与其他正则化方法的数值实验结果比较表明,LSQR法具有良好的稳定性和可靠性 [3-6],已被广泛应用于地震层析成像中[12]。那么能否直接利用其求解位场反问题呢:杨辉等[13]将阻尼LSQR方法引入到重力与地震联合反演中,显示反演结果稳定性好;Ye等[14]将LSQR法应用于航空重力梯度反演,显示其可以提供与Tikhonov正则化几乎相同的效果。但均未给出它与标准Tikhonov正则化求解的详细对比结果,缺少对LSQR法解的分析和评价。

笔者以两个合成模型的重力数据为例,在加入不同的噪声后,分别利用标准的Tikhonov正则化和LSQR法求解反问题,通过两种方法的L曲线特征、解误差范数、拟合残差范数、拟合均方根误差等的对比,以分析直接利用LSQR法求解位场反问题的稳定性和可靠性,并将其应用于四川盆地雅安地区页岩气调查中的重力三维反演,以验证实际应用效果。

1 反演理论

1.1 正则化方法

若将模型空间离散化为若干个单元,反演时单元尺寸保持不变,只求解各单元的密度或磁性,则反问题可写为

Am=d=d˙+ε,

其中:A为核矩阵,它只与单元尺寸及观测点的位置有关;m为待求解的模型向量(密度或磁性);d为观测数据向量;ε为无误差数据 d˙的扰动向量,并服从高斯分布。反演的不适定性表现在:核矩阵A是奇异和病态的;观测数据不可避免地存在误差等。使得式(1)的直接解不唯一且不稳定。这就需要特殊的求解方法:用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,即正则化方法。

目前,直接正则化方法已广泛应用于求解中小型离散不适定问题。其中:Tikhonov正则化方法的思想是求解式(1)的极小范数和最小二乘解,即

minimize{‖Am-b‖22+λ‖Dm‖22},

其中:λ为正则化参数,D为模型约束矩阵,标准的Tikhonov正则化对应D为单位矩阵;TSVD(截断奇异值分解法)的思想是保留核矩阵A大的奇异值对应的分量,舍弃小的奇异值对应的分量,从而避免噪声被过分放大。对于中小规模问题,SVD(奇异值分解)求解方程组稳定可靠,是直接正则化方法求解的理想选择,但对于大规模问题,SVD求解成本过高,其计算量约为O(n3)。

迭代法LSQR和CGLS为基于Krylov子空间投影法,是求解大型线性方程组问题的一种有效途径,同时他们又具有天然的正则化性质,迭代次数即为正则化参数,近年来将其应用离散不适定问题的求解引起了广泛的关注。由于CGLS得到的投影方程组为

ATAm=ATb,

而LSQR得到的方程组就是式(1)本身,前者放大因子是奇异值平方的倒数,因而对于病态线性方程组后者求解结果更好。因此,在文中我们关注LSQR[15]法,其求解思路是首先把任意系数矩阵方程化为系数矩阵为方阵的方程,然后利用Lanczos方法,求解方程的最小二乘解。具有对计算机内存要求低、迭代收敛快和求解结果稳定等优点。其迭代求解算法见表1:

Hilber、Pascal矩阵以及地震层析成像数值实验结果表明,LSQR法较Tikhonov和TSVD正则化稳定可靠[4,5,6]。那么在位场反演中,LSQR法表现究竟如何是笔者所关注的,我们在第2节中将通过合成模型数值实验加以比较分析。

表1   LSQR算法

Table 1  Description of instruction in LSQR algorithm

初始化:
β1μ1=d, α1ν1=ATμ1, ω1=ν1
m0=0, ρ1*=α1, φ1*=β1
for i=1,2,3,…
βi+1μi+1=Aνi-αiμi,
αi+1νi+1=ATui+1-βi+1νi,
ρi=ρi*2+βi+12, ci=ρi*ρi, si=βi+1ρi,
θi+1=siαi+1, φi=ciφi*, ρi+1*=-ciαi+1,
φi+1*=siφi*,
mi+1=mi+φiρiωi, ωi+1=νi+1-θi+1ρiωi
是否达到迭代终止条件。

新窗口打开| 下载CSV


1.2 深度加权约束

重磁异常与场源到观测点之间的距离呈幂次方反比,从而使异常幅值随场源到观测点距离的增加而迅速衰减,不加约束的反演异常往往趋向近地表附近。Li[16,17]等通过在模型约束项中加入一个深度加权函数来克服这种“趋肤效应”,令zj为模型单元中心埋深,在仅考虑深度方向的情况下可写为D=diag{1/(z1)β/2,1/(z2)β/2,…,1/(zM)β/2}。

将基于模型约束的深度加权变换为基于核矩阵的深度加权。令:A*=AD-1,m*=Dm;由于D为对角矩阵,则D-1D=I(I为单位矩阵),式(1)可写为

A*m*=d,

上式可用LSQR法求解,并返回最佳迭代次数的解。

相应地,标准的Tikhonov正则化目标函数可写为

E(m*,λ)=‖A*m*-d‖22+λ‖m*‖22,

根据极值条件,求目标函数E(m,λ)关于模型向量m或mT的偏导数,并令其等于零,可得迭代求解公式。

求得m*后,再根据式m=D-1m*反求模型量。

1.3 正则化参数求解

这里正则化参数包含了Tikhonov正则化与LSQR法,地球物理反演中最常用的有广义交叉检验(GCV)[7-8,11,18]和L曲线法[19,20]。其中,L曲线法就是刻画正则化解ln(‖m‖2)沿残差ln(‖d-Am‖2)的几何曲线,L曲线的拐点处(曲率最大)所对应的正则化参数即为最佳正则化参数,它是一种直观的选取办法。考虑到局部拐点的影响,Hansen等[20]提出求自适应剪枝算法,即考虑不同尺度下一些系列修剪的L曲线特征,从而确定全局拐点。笔者利用L曲线自适应剪枝算法求取Tikhonov与LSQR法的正则化参数。

对于Tikhonov正则化,正则化参数为λ,其L曲线是关于λ的连续函数。我们选取部分对数等间隔点计算ln(‖ mλ*‖2)与ln(‖d-A*mλ*‖2),并利用三次样条函数分别拟合(lnλ,ln(‖ mλ*‖2))与(lnλ,ln(‖d-A*mλ*‖2))曲线,然后求取拟合曲线(ln(‖ mλ*‖),ln(‖d-A*mλ*‖2))的最大曲率点,则最大曲率点所对应的λ即为最佳正则化参数(图1所示)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

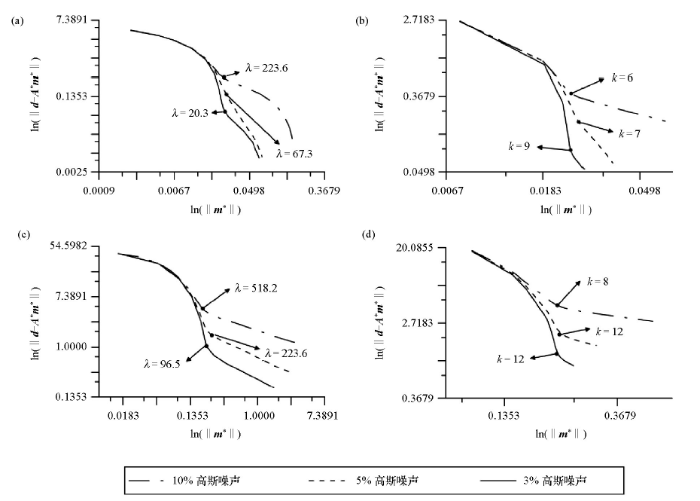
图1   合成模型Tikhonov正则化和LSQR法L曲线

a—单一模型Tikhonov正则化;b—单一模型LSQR法;c—组合模型Tikhonov正则化;d—组合模型LSQR法

Fig.1   The L-curve of Tikhonov regularization and LSQR

a—single model for Tikhonov regularization;b—single model for LSQR;c—complex model for Tikhonov regularization;d—complex model for LSQR


对于LSQR法,迭代次数k即为正则化参数。与Tikhonov正则化参数求取稍有不同,由于迭代次数为等步长增加,可利用差分法求取(ln(‖ mλ*‖),ln(‖d-A*mλ*‖2))曲线的最大曲率点,并返回最大曲率点所对应迭代次数的求解结果。

2 数值实验

2.1 实验过程

利用一个二维单一模型和一个三维组合模型(矩阵病态性更加严重)的正演数据,并分别加入3%、5%和10%的高斯噪声,比较在同一噪声水平、同一正则化参数选取办法以及同一深度加权约束条件下,Tikhonov正则化与LSQR法的求解结果。反演时,模型水平方向剖分与数据一一对应,垂向等间距剖分(间距50 m)21层,且无密度范围约束。为便于比较分析,排除迭代解误差对反演结果的影响,采用SVD法求解Tikhonov正则化中的线性方程组。

其中:单一模型为一个剩余密度为1 g/cm3、顶面埋深200 m,沿X轴范围900~1 100 m,截面为正方型的二度体,数据点距为50 m,共41个数据,式(4)中的矩阵A*在2-范数下其条件数为942.3,最小与最大奇异值比值10-3;组合模型为两个倾斜方向相反的三度脉状异常体,长脉状体(B2)剩余密度1 g/cm3,短脉状体(B1)剩余密度0.8 g/cm3,X方向点距50 m,Y方向点距100 m,共861个数据,矩阵A*在2-范数下其条件数为4.4×107,最小与最大奇异值比值2.3×10-8,相比前者,矩阵的病态性更加严重。

2.2 实验结果分析

图1为不同噪声水平下,Tikhonov正则化和LSQR法的L曲线图。两种方法的L曲线图相似点表现为:最佳正则化参数或迭代次数与数据噪声水平相关,对于Tikhonov正则化,数据噪声越大,最佳正则化参数也越大,LSQR法则反之,这是兼顾分辨率与方差的必然结果;对于较大的正则化参数或较小的迭代次数,不同噪声数据的解残差范数以及模型范数差别不大,L曲线基本重合,即近似解中正则化误差占主导地位;随着正则化因子的减小或迭代次数的增加,噪声越大的数据其求解的模型范数越大,而解残差范数的减小幅度则越小,体现了近似解中数据扰动误差逐渐占主导地位。不同点则表现为:Tikhonov最佳正则化参数随数据噪声的增大而变化范围较大,LSQR法最佳迭代次数随数据噪声的增大而变化范围小(变化范围仅为9~6或之间12~8之间),这意味着LSQR法的解随数据扰动误差的增大而变化缓慢,与文献[5]中关于Hilbert矩阵实验结果一致,显示出较强的稳定性。

令模型绝对误差Ae=‖mtrue-m‖2,mtrue为真实解;解残差r=‖d-Am‖2;拟合均方跟根误差

Rms=∑i=1N(di-di*)2/di2N,

其中:d*为计算数据,N为数据个数。

表1为不同噪声水平下,Tikhonov和LSQR正则化方法的求解结果。两种正则化方法的Rms与数据误差基本保持在同一水平上,r、Ae数值相近。若以Tikhonov正则化求解结果为基准,则Ae相对误差最大仅为0.36%,说明直接利用LSQR求解位场反问题,能够得到满意的正则化解。

表2   合成模型Tikhonov和LSQR正则化求解结果

Table 2  The ruslts of synthetic models for Tikhonov and LSQR regularization

模型噪声
水平		TikhonovLSQR
λrλAeλRmskrkAekRms
3%20.30.06093.73471.43%90.09483.72712.79%
单一模型5%67.30.12603.70973.02%70.18823.69644.94%
10%223.60.34823.73387.10%60.39923.72109.32%
3%96.51.095625.51642.49%121.243325.53163.27%
组合模型5%223.62.072025.54184.62%122.107925.50317.20%
10%518.24.283025.614814.59%84.358025.633610.46%

新窗口打开| 下载CSV


此外,式(5)还可利用LSQR法求解,并令λ为对应的最佳Tikhonov正则化参数(如:组合模型加入10%的噪声数据,λ=518.2),此时LSQR法的L曲线图为“┐”型,即随着迭代次数增大,解残差范数逐渐减小,而模型范数基本不变。相应的,若给定一组正则化参数,利用LSQR法求解式(5),并返回最佳迭代次数结果,则Tikhonov正则化的L曲线图同样表现为“┐”型。进一步说明,对于位场反问题,LSQR法与Tikhonov正则化具有同等效果,可直接利用LSQR法求解位场反问题而不需添加额外的正则化方法。

2.3 LSQR法反演效果

这里给出组合模型在加入10%的高斯噪声后LSQR法反演结果。由图2可见,尽管加入噪声后的数据等值线图(图2b)显得杂乱且等值线呈锯齿状跳跃,但其反演计算数据等值线图(图2c)则显得光滑且有规律,与无误差数据等值线图(图2a)具有可比性。由LSQR成像结果可见(图3),无论XY平面还是XZ剖面都很好地恢复了真实模型的基本轮廓。

图2

新窗口打开| 下载原图ZIP| 生成PPT

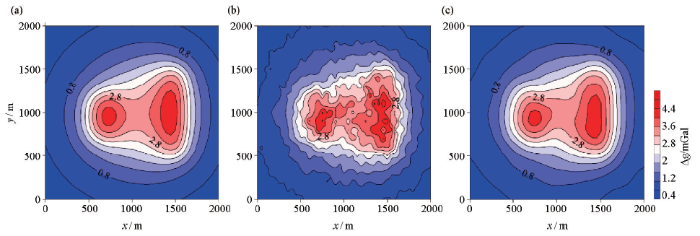
图2   组合模型数据等值线(等值线间距:0.4 mGal)

a—无误差数据;b—加入10%高斯噪声数据;c—反演模型计算数据

Fig.2   Map of composite model data contour (isoline interval:0.4mGal)

a—datas without deviation;b—datas with 10% gauss noise models;c—datas of inversion model


2.4 LSQR法与Tikhonov正则化计算成本对比

1) LSQR法仅涉及到矩阵与向量的乘积,本身具有降维的特点,且无需显示式地表示出核矩阵,方便利用矩阵分块思想结合快速正演方法[21,22,23,24]实现大规模位场三维反演。而Tikhonov正则化则需显示式地计算存储核矩阵,且由于核矩阵为大型稠密的,需要进行压缩存储[2,10-11]等特殊处理以减少对计算机内存的消耗。

2) LSQR法只需从已有迭代解中选择最优的迭代次数解。对于Tikhonov正则化,即便利用L曲线法确定最佳正则化参数,每反演迭代一次,也至少需4个已知正则化参数(对应L曲线上两个垂直方向的点与两个水平方向的点),而每个正则化参数的计算又相当于一次反演计算,因此每反演迭代一次,其计算量至少是LSQR法的4~5倍。

3) 利用LSQR求解线性方程组,一般情况下迭代次数k<min(M,N),M、N为系数矩阵的维数。如果利用其正则化性质,则最佳迭代次数会更小(如3.2节中的组合模,M=16 800、N=861,最佳迭代次数最大仅为12次),实际应用中可根据L曲线的实时形态,确定一个较大的终止迭代次数,然后计算最大曲率点,并返回最大曲率对应的迭代次数解,无疑进一步提高了计算效率。

图3

新窗口打开| 下载原图ZIP| 生成PPT

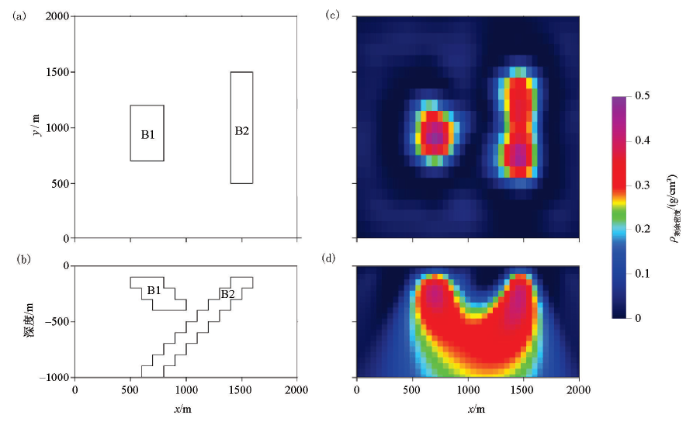
图3   组合模型及其LSQR法反演结果

a—组合模型XY平面切片(深度100 m);b——组合模型XZ剖面切片(Y=1000 m);c—XY平面切片图的反演结果;d—XZ剖面切片图的反演结果

Fig.3   Complex of model and the inversion results

a—the plan slices of the XY-plane(depth of 100m);b—the plan slices of the XZ-profile(Y=1000 m);c—the LSQR inversion result of the plan slices of the XY-plane(depth of 100m);d—the LSQR inversion result of the plan slices of the XZ-profile(Y=1000 m)


3 实例数据反演

3.1 地质概况

以四川盆地雅安地区重力数据为例,利用LSQR法反求地下三维空间密度结构,进而为页岩气靶区优选提供资料支撑。

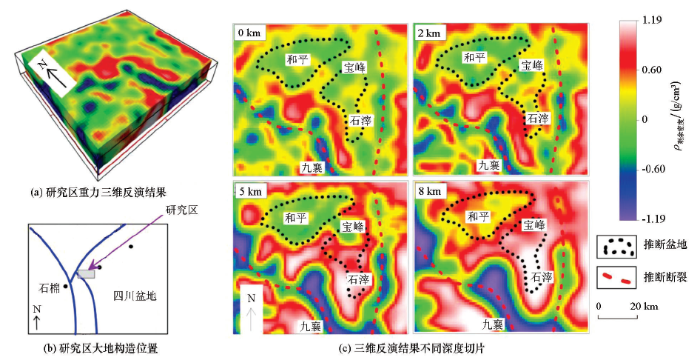
研究区位于上扬子板块西缘,是四川盆地与川滇隆起的过渡区域(图4b)。全区地层较为发育,缺失石炭系地层。上奥陶统五峰组—下志留统龙马溪组广泛发育于扬子前陆隆起与前缘隆起之间的坳陷盆地内,主要为黑色笔石页岩和放射虫硅质岩。雅安地区志留系龙马溪组具有普遍发育、层位连续性好、厚度大,埋深适中,有机质含量高等特点,是理想的页岩气勘探区块。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   四川雅安地区三维重力反演结果

Fig.4   The 3D inversion of gravity in Ya’an area of Sichuan basin


物性测试统计结果表明,区内沉积岩相对变质岩以及火成岩表现为低密度特征,从而为利用重力资料划分沉积盆地奠定了基础。对区内1∶20万重力资料进行三维反演,以明确沉积盆地的横向及纵向分布范围。

3.2 反演结果

研究区范围90 km×75 km,布格重力全为负值,异常幅值变化范围为-230~-330 mGal,布格重力异常从四川盆地往青藏高原板块方向逐渐减低,异常形态为SN走向的低缓重力梯度带。我们利用网格化(网度:1.5 km×1.5 km)后的数据采用滑动平均法求取剩余异常(软件为GMS3.0),并利用剩余异常进行反演计算。模型水平向剖分与数据网格一一对应,垂向等间距剖分为20层,每层厚0.5 km,数据量3 000个,模型单元数60 000个。为进一步节省计算成本,笔者结合等效几何格架技术,将大矩阵按照模型单元划分为若干个子矩阵进行存储与运算,在普通笔记本电脑(品牌:Dell;处理器:Inter i5-6300;主频:2.3 GHz;内存:8 GB)上运行,LSQR法共迭代80次,总耗时66 min,最后根据L曲线特征取第42次迭代结果作为反演结果,最后利用三维成图软件建立研究区内三维剩余密度体。

图4c为不同深度(0、2、5、8 km)的剩余密度切片,根据岩石密度特征,反演异常初步解释为:大范围的低密度异常主要为沉积岩的响应;高密度异常主要为火山岩或变质岩的反应;而条带状、串珠状的低密度异常则主要为断裂带的响应。基于上述分析,结合地质资料,划分了两个沉积盆地(和平盆地、宝峰—石滓盆地)和两条深大断裂。其中:和平盆地纵深明显大于宝峰—石滓盆地,大地电磁测深资料处理结果也证实上述推断[25]。综合而言,宝峰—石滓盆地更利于页岩气的勘探开发。本次重力三维反演取得的成果为后续页岩气靶区优选提供了有力支撑。

4 结论

1) 合成模型数值实验结果表明:LSQR法与Tikhonov正则化方法的解误差范数、拟合残差范数数值相近, 其解模型相对Tikhonov正则化,最大相对误差仅为0.36%;对于较大的噪声数据(10%的高斯噪声),LSQR法依然能够得出较好的正则化解;说明可直接利用LSQR求解位场反问题而无需添加额外的正则化方法。

2) 实验表明:相比Tikhonov正则化,LSQR法的最佳正则化参数(迭代次数)随数据噪声的变化而变化缓慢,表现出良好的稳定性。

3) Tikhonov正则化需显示式地计算存储核矩阵、且需通过多次计算选择正则化参数等,对于大型问题求解成本过高。LSQR法则无需显示地表示出核矩阵,只需从已有迭代计算结果中选取最佳正则化解,其本身也具有计算成本低的特点,因而LSQR法更适合于求解大型位场反问题。

4) 将LSQR法应用于四川盆地雅安地区重力三维反演,结合等效几何格架技术将大矩阵分为若干个子矩阵进行存储与运算,极大地节省了计算成本。并据反演结果划分了两个沉积盆地和两条深大断裂,为页岩气靶区优选提供了资料支撑。

The authors have declared that no competing interests exist.
作者已声明无竞争性利益关系。

参考文献

管志宁 . 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.

[本文引用: 2]

Guan Z N .

Geomagnetic field and magnetic exploration

[M]. Beijing:Professor of Geophysics, 2005.

[本文引用: 2]

刘天佑 . 位场勘探数据处理新方法[M]. 北京: 科学出版社, 2007.

[本文引用: 2]

Liu T Y. New data processing methods for potential field exploration[M]. Beijing: Science Press, 2007.

[本文引用: 2]

刘伊克, 常旭 .

地震层析成像反演中解的定量评价及其应用

[J]. 地球物理学报, 2000,43(2):251-256.

DOI:10.3321/j.issn:0001-5733.2000.02.013      URL     Magsci     [本文引用: 2]

对地震层析成像非线性问题线性化处理之后，各种反演算法归纳成为对不适定方 程的求解．地震层析成像反演算法的解的物理意义是给出地质结构，因此对于解的可靠性及 分辨率研究非常重要．然而许多反演算法不能给出解的评价方法，因而对解的可信度产生怀 疑．本研究根据解估计的分辨率矩阵的原理，提出ＬＳＱＲ（Ｌｅａｓｔ Ｓｑｕａｒｅ ＱＲ）算法解协方差矩 阵的评价算法，用相关分析可以为那些在求解过程中得不到分辨率矩阵的反演方法提供解的 定量评价．并用本文提出的解的定量评价方法试评了一个实际地壳模型的地震层析成像的 速度重建结果．

Li Y K, Chang X .

Quatitative asessment of invension solution of seismic tomographys and its applicatiom

[J]. Chinese Journal of Geophysics, 2000,43(2):251-256.

Magsci     [本文引用: 2]

潘克家, 王文娟, 谭永基 , 等.

基于混合差分进化算法的地球物理线性反演

[J]. 地球物理学报, 2009,52(12):3083-3090.

DOI:10.3969/j.issn.0001-5733.2009.12.017      URL     Magsci     [本文引用: 1]

<FONT face=Verdana>地球物理反问题线性化处理之后, 各种反演算法归结为对病态线性方程组的求解. 为了快速准确地计算出地球物理参数, 本文提出了一种全新的基于LSQR算法的混合差分进化算法(Hybrid Differential Evolution Algorithm, HDE). 该算法利用LSQR算法给出DE算法的初始种群, 提高DE算法的计算速度和稳定性. 在不同噪声水平下, 对四种正则化方法Tikhonov、TSVD、LSQR和HDE的反演结果进行详细比较. 理论模型和实际数据反演的结果都表明: 改进的HDE算法应用于地球物理反问题的求解是成功的: 反演结果与原设定模型具有较高的相关性, 在稳定性和准确性上较常规的反演算法都具有一定的优势; 而且不需要给定正则化参数, 具有更强的实用性.</FONT>

Pan K J, Wang W J, Tan Y J , et al.

Geophysical linear inversion based on hybrid differential evolution algorithm

[J]. Chinese Journal of Geophysics, 2009,52(12):3083-3090.

Magsci     [本文引用: 1]

常旭, 卢孟夏, 刘伊克 .

地震层析成像反演中3种广义解的误差分析与评价

[J]. 地球物理学报, 1999,42(5):695-701.

DOI:10.3321/j.issn:0001-5733.1999.05.013      URL     Magsci     [本文引用: 2]

在地震波速度和地震波　值层析成像中，对于非线性反演问题解的可靠性研究非常重要．为了讨论ＡＲＴ（ＡｌｇｅｂｒａｉｃＲｅｃｏｎｓｔｒｕｃｔｉｏｎ　Ｔｅｃｈｎｉｑｕｅ）、ＳＶＤ（Ｓｉｎｇｕｌａｒ　ＶａｌｕｅＤｅｃｏｍｐｏｓｉｔｉｏｎ）、ＬＳＱＷ（ＬｅａｓｔＳｕａｒｅ）３种方法的算法稳定性以及反演效果，本研究将这３种算法用于求解非常病态问题和一般稳定问题，根据数值计算结果，分别给出了在非常病态问题和一般稳定问题中３种算法的相对误差及其算法稳定性评价．进而针对３种算法在同一地质模型上的速度成像结果进行了比较，为地震层析成像反演效果分析提供了定量参数．

Chang X, Lu M X, Liu Y K .

Error analysis and appraisals for three general solution in seismic tomography

[J]. Chinese Journal of Geophysics, 1999,42(5):695-701.

Magsci     [本文引用: 2]

Leiss E L, Pan J M,

曹辉.含噪声数据的各种地球物理层析成象反演技术的比较

C]//美国勘探地球物理学家学会年会, 1992: 147-156.

URL     [本文引用: 3]

地球物理层析成象经常受到欠定和矛盾方程组的困扰。因此,必须对数据误差的传播加以控制。计算中,不同的反演方法对数据的依赖关系有所不同,误差传播数量也有变化。我们试验了三种反演方法: (1)奇异值分解(SVD),这是一种广泛应用于全方位地震层析成象中的反演技术。 (2)最小平方算法(LSQR)中的共轭梯度迭代法,它应用Golub与Kahan的双对角线化技术迭代地清除估算值与真值的差。 (3)正交化方法(ORTH),这是B．Rust,W．R．Burrus和C．Schneeberger 提出的一种分解法,它用广义Gramm—Schmidt正交化技术,并用最小长度准则解反问题。实验证明,如果数据没有误差,所有三种算法得到的结果都与原始模型很接近。LSQR 与ORTH比SVD收敛的快,特别是在大模型(即模型中有大量的交叉射线和模型板块) 情况。当数据有误差时,LSQR与ORTH比SVD可靠,而且在恢复欠定部分时,LSQR 与ORTH也比SVD稳定。

Leiss E L, Pan J M, Cao H .

Comparison of geophysical inversion technology with noise data

C]//SEG, 1992: 147-156

[本文引用: 3]

Abedi M, Gholami A, Norouzi G H , et al.

Fast inversion of magnetic data using Lanczos bidiagonalization method

[J]. Journal of Applied Geophysics, 2013,90(90):126-137.

DOI:10.1016/j.jappgeo.2013.01.008      URL     [本文引用: 2]

This paper describes application of a fast inversion method to recover a 3D susceptibility model from magnetic anomalies. For this purpose, the survey area is divided into a large number of rectangular prisms in a mesh with unknown susceptibilities. Solving the full set of equations is substantially time consuming, and applying an algorithm to solve it approximately can reduce the time significantly. It is shown that the Lanczos bidiagonalization method can be an appropriate algorithm to solve a Tikhonov cost function for this purpose. Running time of the inverse modeling significantly decreases by replacing the forward operator matrix with a matrix of lower dimension. A weighted generalized cross validation method is implemented to choose an optimum value of a regularization parameter. To avoid the natural tendency of magnetic structures to concentrate at shallow depth, a depth weighting is applied. This study assumes that there is no remanent magnetization. The method is applied on a noise-corrupted synthetic data to demonstrate its suitability for 3D inversion. A case study including ground based measurement of magnetic anomalies over a porphyry-Cu deposit located in Kerman providence of Iran, Now Chun deposit, is provided to show the performance of the new algorithm on real data. 3D distribution of Cu concentration is used to evaluate the obtained results. The intermediate susceptibility values in the constructed model coincide with the known location of copper mineralization.

Rezaie M, Moradzadeh A, Kalateh A N .

Fast 3D inversion of gravity data using solution space priorconditioned lanczos bidiagonalization

[J]. Journal of Applied Geophysics, 2017,136:42-50.

DOI:10.1016/j.jappgeo.2016.10.019      URL     [本文引用: 1]

61The required time and memory for gravity data inversion can be decreased by priorconditioned lanczos bidiagonalization.61The orthonormal basis vectors of the discrete cosine transform can be applied for solution space priorconditioning.61We performed a number of inversions of synthetic and real cases, the proposed method works for fast inversion of the data.

Portniaguine O, Zhdanov M S .

3-D magnetic inversion with data compression and image focusing

[J]. Geophysics, 2002,67(5):1532-1541.

DOI:10.1190/1.1512749      URL    

Pilkington M .

3-D magnetic imaging using conjugate gradients

[J]. Geophysics, 1997,62(4):1132-1142.

DOI:10.1190/1.1444214      URL     [本文引用: 1]

Li Y G, Oldenburg D W .

Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method

[J]. Geophysical Journal International, 2003,152(2):251-265.

DOI:10.1046/j.1365-246X.2003.01766.x      URL     [本文引用: 3]

In this paper wavelet transforms and a logarithmic barrier method are applied to the inversion of large-scale magnetic data to recover a 3-D distribution of magnetic susceptibility. The fast wavelet transform is used, along with thresholding the small wavelet coefficients, to form a sparse representation of the sensitivity matrix. The reduced size of the resultant matrix allows the solution of large problems that are otherwise intractable. The compressed matrix is used to carry out fast forward modelling by performing matrix-vector multiplications in the wavelet domain. The reduction in CPU time is directly proportional to the compression ratio of the matrix. A second important feature of the algorithm used here is the use of an interior-point method of optimization to enforce positivity constraints. In this approach, the positivity is incorporated into the inversion by a sequence of non-linear optimizations approximated by truncated Newton steps. At the heart of the algorithm, a linear system of equations is solved. The conjugate gradient technique has been used as the basic solver to take the advantage of the efficient forward modelling offered by the sparse matrix representation. Overall, the combination of wavelet transforms, interior point optimization and conjugate gradient solutions readily allows us to solve magnetic inverse problems that have a few hundred thousand parameters and tens of thousands of data.

杨文采, 杜剑渊 .

层析成像新算法及其在工程检测上的应用

[J]. 地球物理学报, 1994,37(2):239-244.

DOI:      URL     Magsci     [本文引用: 1]

基于走时和振幅的层析成像反演涉及大型稀疏矩阵方程的求解，当矩阵严重病态时，目前流行的正交分解型迭代算法难以取得良好的成像效果．本文介绍一种改进的ＬＳ<sub>ｑ</sub>Ｒ算法，即带阻尼的ＬＳ<sub>ｑ</sub>Ｒ迭代算法，它应用在北京机场高速公路桥墩施工质量检测中，取得了良好的效果．

Yang W C, Du J Y .

A new algorithm of seismic tomography with application to engineering detections

[J]. Chinese Journal of Geophysics, 1994,37(2):239-244.

Magsci     [本文引用: 1]

杨辉, 戴世坤, 牟永光 .

三维重力地震剥层联合反演

[J]. 石油地球物理勘探, 2004,39(4):468-471.

DOI:10.3321/j.issn:1000-7210.2004.04.020      URL     Magsci     [本文引用: 1]

以地震资料解释的三维构造图作为模型,用重力三维正演剥离基底及基底以上界面所产生的重力效应,然后对分离后的基底岩性异常进行反演求取基底密度。在具体联合反演算法上,首次将广泛用于地震层析成像反演的DLSQR法引入位场反演,不仅增加了联合反演结果的稳定性,而且极大地提高了反演速度。理论模型的试算和实际资料的反演结果表明,两者反演的剩余密度等值线图形十分相似,剩余密度最小值和最大值相对误差小于4%。

Yang H, Dai S K, Mu Y G .

Joint Layer-stripped inversion of 3-D gravity and seismic data

[J]. Oil Geophysical Prospecting, 2004,39(4):468-471.

Magsci     [本文引用: 1]

Ye Z, Tenzer R, Sneeuw N .

Comparison of methods for a 3-D density inversion from airborne gravity gradiometry

[J]. Studia Geophysica Et Geodaetica, 2017: 1-16.

DOI:10.1007/s11200-016-0492-6      URL     [本文引用: 1]

In this study, we apply Tikhonov’s regularization algorithm for a 3-D density inversion from the gravity-gradiometry data. To reduce the non-uniqueness of the inverse solution (carried out without additional information from geological evidence), we implement the depth-weighting empirical function. However, the application of an empirical function in the inversion equation brings the bias problem of the regularization factor when a traditional Tikhonov’s algorithm is applied. To solve the bias problem of regularization factor selection, we present a standardized solution that comprises two parts for solving a 3-D constrained inversion equation, specifically the linear matrix transformation and Tikhonov’s regularization algorithm. Since traditional regularization techniques become numerically inefficient when dealing with large number of data, we further apply methods which include the Simultaneous Iterative Reconstruction Technique (SIRT) and the wavelet compression combined with Least Squares QR-decomposition (LSQR). In our simulation study, we demonstrate that SIRT as well as the wavelet compression plus LSQR algorithm improve the computation efficiency, while provide results which closely agree with that obtained from applying Tikhonov’s regularization. In particular, the algorithm of wavelet compression plus LSQR shows the best computing efficiency, because it combines the advantages of coefficients compression of big matrix and fast solution of sparse matrix. Similar findings are confirmed from the vertical gravity gradient data inversion for detecting potential deposits at the Kauring (near Perth, Western Australia) testing site.

Paige C C, Saunders M A .

LSQR:An algorithm for sparse linear equations and sparse least squares

[J]. Acm Transactions on Mathematical Software, 1982,8(1):43-71.

DOI:10.1145/355984.355989      URL     [本文引用: 1]

ABSTRACT An iterative method is given for solving Ax ~ffi b and minU Ax- b 112, where the matrix A is large and sparse. The method is based on the bidiagonalization procedure of Golub and Kahan. It is analytically equivalent to the standard method of conjugate gradients, but possesses more favorable numerical properties. Reliable stopping criteria are derived, along with estimates of standard errors for x and the condition number of A. These are used in the FORTRAN implementation of the method, subroutine LSQR. Numerical tests are described comparing I~QR with several other conjugate-gradient algorithms, indicating that I~QR is the most reliable algorithm when A is ill-conditioned. Categories and Subject Descriptors: G.1.2 [Numerical Analysis]: ApprorJmation--least squares approximation; G.1.3 [Numerical Analysis]: Numerical Linear Algebra--linear systems (direct and

Li Y G, Oldenburg D W .

3-D inversion of magnetic data

[J]. Geophysics, 1996,61(2):394-408.

DOI:10.1190/1.1443968      URL     [本文引用: 1]

Li Y G, Oldenburg D W .

3-D inversion of gravity data

[J]. Geophysics, 1998,63(1):109-119.

DOI:10.1190/1.1444302      URL     [本文引用: 1]

Golub G H, Heath M, Wahba G .

Generalized cross-validation as a method for choosing a good ridge parameter

[J]. Technometrics, 1979,21:215-223.

DOI:10.1080/00401706.1979.10489751      URL     [本文引用: 1]

Consider the ridge estimate (0203) for 0205 in the model unknown, (0203) = (XTX + n0203I)0908081XTy. We study the method of generalized cross-validation (GCV) for choosing a good value for 0203 from the data. The estimate is the minimizer of V(0203) given by

Hansen P C .

Analysis of discrete Ill-posed problems by means of the L-curve

[J]. Siam Review, 1992,34(4):561-580.

DOI:10.1137/1034115      URL     [本文引用: 1]

When discrete ill-posed problems are analyzed and solved by various numerical regularization techniques, a very convenient way to display information about the regularized solution is to plot the norm or seminorm of the solution versus the norm of the residual vector. In particular, the graph associated with Tikhonov regularization plays a central role. The main purpose of this paper is to advocate the use of this graph in the numerical treatment of discrete ill-posed problems. The graph is characterized quantitatively, and several important relations between regularized solutions and the graph are derived. It is also demonstrated that several methods for choosing the regularization parameter are related to locating a characteristic L-shaped "corner" of the graph.

Hansen P C, Jensen T K, Rodriguez G .

An adaptive pruning algorithm for the discrete L-curve criterion

[J]. Journal of Computational & Applied Mathematics, 2007,198(2):483-492.

DOI:10.1016/j.cam.2005.09.026      URL     [本文引用: 2]

We describe a robust and adaptive implementation of the L-curve criterion. The algorithm locates the corner of a discrete L-curve which is a log og plot of corresponding residual norms and solution norms of regularized solutions from a method with a discrete regularization parameter (such as truncated SVD or regularizing CG iterations). Our algorithm needs no predefined parameters, and in order to capture the global features of the curve in an adaptive fashion, we use a sequence of pruned L-curves that correspond to considering the curves at different scales. We compare our new algorithm to existing algorithms and demonstrate its robustness by numerical examples.

姚长利, 郝天珧, 管志宁 , 等.

重磁遗传算法三维反演中高速计算及有效存储方法技术

[J]. 地球物理学报, 2003,46(2):252-258.

DOI:10.3321/j.issn:0001-5733.2003.02.020      URL     Magsci     [本文引用: 1]

将地下场源区域规则划分成很多小长方体单元，并且通过反演确定这些单元的物性变 化，勾画出场源的分布图像，这种方式逐步成为重磁反演，特别是三维反演的重要方向；遗 传算法等非线性技术进行该类反演将逐步成为发展趋势. 本文指出，在应用遗传算法进行该 类反演过程中，隐含着数据量较大时超常规的计算量，它已成为制约该类反演充分发挥作用 的瓶颈问题；同时，本文提出了针对性的分离并存储几何格架的计算策略、以及独特的几何 格架等效压缩存储技术，可以从根本上提高非线性反演计算速度，为该类反演的有效应用奠 定了坚实的基础.

Yao C L, Hao T Y, Guan Z N, Zhang Y W .

High-speed computation and efficient storage in 3-D gravity and magnetic inversion based on genetic alogorithms

[J]. Chinese Journal of Geophysics, 2003,46(2):252-258.

Magsci     [本文引用: 1]

姚长利, 郑元满, 张聿文 .

重磁异常三维物性反演随机子域方法技

[J]. 地球物理学报, 2007,50(5):1576-1583.

DOI:10.3321/j.issn:0001-5733.2007.05.035      URL     Magsci     [本文引用: 1]

<FONT face=Verdana>本研究针对三维物性反演中存在的困难和问题，提出三维物性反演的随机子域方法技术，首先是将正反演中保持不变的几何格架分离计算并存储，避免重复计算，从而提高正反演计算速度；其次是利用对称性等实现等效计算，明显降低格架计算和存储要求；再通过随机子域方式，降低反演的维数问题；另外，通过概率方式控制子域生成的分布，实现约束新机制. 模型和实例计算表明了方法技术的效果，为大面积重磁数据的三维反演提供了有效的途径. </FONT>

Yao C L, Zheng Y M, Zhang Y W .

3-D gravity and magnetic inversion for physical properties using stochastic subspaces

[J]. Chinese Journal of Geophysics, 2007,50(5):1576-1583.

Magsci     [本文引用: 1]

侯遵泽, 杨文采, 刘家琦 .

中国大陆地壳密度差异多尺度反演

[J]. 地球物理学报, 1998,41(5):642-651.

URL     Magsci     [本文引用: 1]

利用小波分析方法原理，在对中国布格重力异常多尺度分解的基础上，反演了各种尺度意义下中国大陆地壳的密度差异，给出了中国大陆地壳中相对密度差异的空间分布，为研究中国大陆地壳构造、进行深部地质研究提供了新结果．

Hou Z Z, Yang W C, Liu J Q .

Multiscle inversion of the density contrast within the crust of China

[J]. Acta Geophysica Sinica, 1998,41(5):642-651.

Magsci     [本文引用: 1]

吴文鹂, 高艳芳, 顾观文 .

起伏地形重磁三维快速正演计算

[J]. 物探化探计算技术, 2009,31(3):179-182.

DOI:10.3969/j.issn.1001-1749.2009.03.002      URL     [本文引用: 1]

正演是反演技术的基础,正演速度和求解反演问题的系数矩阵存放一直是起伏地形下重、磁三维反演的关键技术问题。这里提出了一种起伏地形下重磁快速正演计算方法,其计算原理是根据反演在垂向的剖分层数,利用水平地形正演计算形成二个不同大小刻度标尺矩阵,然后在模型空间,使用分段线性插值的方式,直接计算出起伏地形观测点的正演值。该方法的主要特点是在保持很高的计算精度下计算速度可提高二倍,且节省计算内存,适合起伏地形下重磁三维反演技术研究。

Wu W L, Gao Y F, Gu G W .

Gravity and magnetic 3D fast forward computing with rolling topography

[J]. Computing Techniques for Geophyscal and Geochemcal Exploration, 2009,31(3):179-182.

[本文引用: 1]

王桥, 郭镜, 王永华 , 等.

四川盆地雅安地区页岩气靶区优选——来自非震地球物理的证据

[G]. 中国地质学会2017年学术年会论文摘要汇编(下册), 2017: 219-221.

[本文引用: 1]

Wang Q, Guo J, Wang Y H , et al.

Shale gas target selection in Ya’an area, Sichuan:Evidence from non-seismic geophysics[G]

2017 Conference of Geological Society Of China, 2017, 2019-221.

[本文引用: 1]

梁生贤 .

互相关系数自约束的重力三维反演与高效求解

吉林大学学报:地球科学版, 2018,48(5):1473-1482.

DOI:10.13278/j.cnki.jjuese.20170167      URL    

本文将拟合残差计算所得的互相关系数作为先验信息,与深度加权函数同时引入到重力正则化反演的模型约束中,以提升反演结果的可靠性。针对三维反演中的大型线性方程组问题,引入阻尼LSQR(最小二乘QR分解)算法,结合等效几何格架技术,将大矩阵按照模型单元划分为若干个子矩阵进行存储与运算。理论模型计算结果表明:同时利用互相关系数和深度加权的模型自约束反演,能较清晰地反映真实异常体;基于分块矩阵的阻尼LSQR算法求解线性方程组较直接法节省了几千甚至上万倍的存储量,且计算速率提高了数倍,可在普通计算机上实现较大规模的反演计算。将其应用于云南芦子园铁铅锌铜多金属矿床隐伏花岗岩体定位,取得了良好的效果。

Liang S X .

A self-constrained 3D inversion of gravity data based on cross-correlation coefficient method and efficient solver

[J]. Journal of Jilin University:Earth Science Edition, 2018,48(5):1473-1482.

焦彦杰, 黄旭日, 李光明 , 等.

藏南扎西康矿集区深部结构与成矿:来自地球物理的证据

[J].地球科学.

Jiao Y J, Huang X R, Li G M , et al.

Deep Structure and mineralization of the Zhaxikang Ore-concentration area,Southern Tibet:evidence from geophysics

[J/OL].Earth Science.

URL    

梁生贤, 焦彦杰, 樊文鑫 , 等 .

基于LSQR 法与相关系数自约束的磁异常三维反演

[J].地球物理学进展.

Liang S X, Jiao Y J, Fan W X , et al.

3D inversion of magnetic data based on LSQR method and correlation coefficient self constrained

[J/OL].Progress in Geophysics.

URL    

郭镜, 李文昌, 李光明 , 等.

多尺度综合地球物理方法在扎西康铅锌锑金多金属矿找矿预测中的应用

[J].地球科学.

Guo J, Li W C, Li G M ,et al.

Application of multi-scale integrated geophysical method in prospecting prediction of Zhaxikang Pb-Zn-Sb-Au polymetallic deposit

[J/OL].Earth Science.

URL    

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com