0 引言
地震波旅行时是研究地震波传播的一个关键属性参数,在地震波反演、叠前偏移、层析成像等研究领域发挥着重要的作用,旅行时的计算精度、效率、稳定性直接影响着以上各个领域的研究效果、效率及应用范围[1]。因此,研究如何提高地震波旅行时精度具有重大的意义。
计算地震波旅行时通常采用射线追踪法,而有关射线追踪的方法有很多种,其中主要包括传统的射线追踪法(打靶法和弯曲法)、最短路径法、有限差分法等等。传统的射线追踪法缺陷在于计算量大,存在盲区,且全局最小值难确定[2];最短路径法虽然避免了传统方法的一些缺陷,计算精度高,但非常耗时且需要巨大的储存空间[3];Vidale提出的基于程函方程的有限差分法[4]开辟了地震波旅行时计算的新道路,与之前的方法相比最显著的优势是计算速度快,但算法不稳定,也不符合波前传播的规律[5]。基于有限差分法的缺陷,后人对其进行了大量的研究和改进,Sethian等提出了具有迎风差分格式的快速行进法(FMM)[6],它具有无条件稳定、易于编程实现等优点,且满足波前传播的规律[7],被当今地震波初至计算广泛应用。
FMM受差分算法自身缺陷的影响,其精度主要受限于网格剖分大小和差分格式阶数。对于这两个因素,许多学者对其进行了研究与改进:Rawlinson等比较了一阶、二阶、三阶差分格式的计算精度和效率,指出一阶精度最低,而计算效率最高,二阶、三阶精度相当,但二阶的计算效率远远高于三阶[8];张风雪等根据时间场梯度大小对射线路径求取的影响,引入了方向参数[9],能够有效控制解的精度,同时也控制网格计算量;孙章庆研究复杂地表条件下的旅行时,发现FMM计算相对误差集中在震源附近,且误差分布具有方向性,据此提出了改进的一阶FMM,提高了旅行时计算精度和效率[10];李永博等在孙章庆研究的基础上,提出了多种FMM改进措施,其中引入了角点因素及双重网格[11]。本文在前人研究成果的基础上,进一步改进FMM的精度,提出了变网格FMM。首先阐述FMM基本原理、变网格差分格式、窄带技术原理;其次建立均匀正演模型,比较常规一阶、二阶FMM、变网格一阶、二阶FMM、双重网格一阶FMM计算地震波旅行时的精度,指出变网格FMM的优势;再次,建立存在高速异常体的正演模型,指出变网格FMM较双重网格FMM的优势;最后,应用复杂的Marmousi模型说明变网格FMM的适应性。该方法不仅提高了地震旅行时的精度,还大大缩短了计算时间,为地震波反演、叠前偏移、层析成像等研究成果的可靠性奠定了基础。
1 基本原理
1.1 FMM基本原理
FMM是一种满足“熵守恒”的迎风差分格式和窄带技术相结合的非迭代算法。在二维情况下,地震波旅行时满足程函方程,具体表达式为:
式中:t为地震初至波旅行时,s为介质慢度。
计算地震波旅行时时,采用迎风差分格式对式(1)进行离散,其表达式[12]为:
式中:
1.2 变网格FMM差分格式
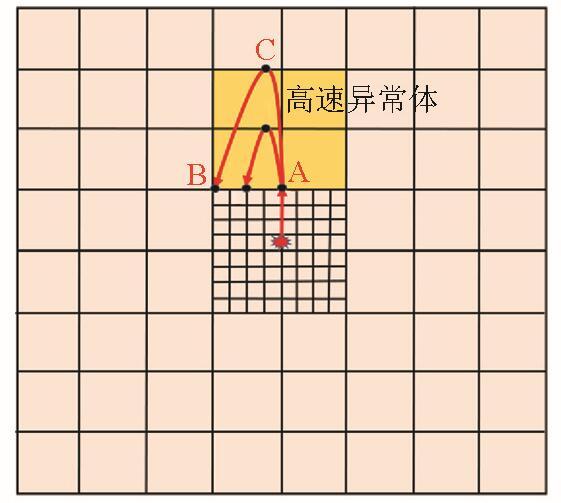
图1
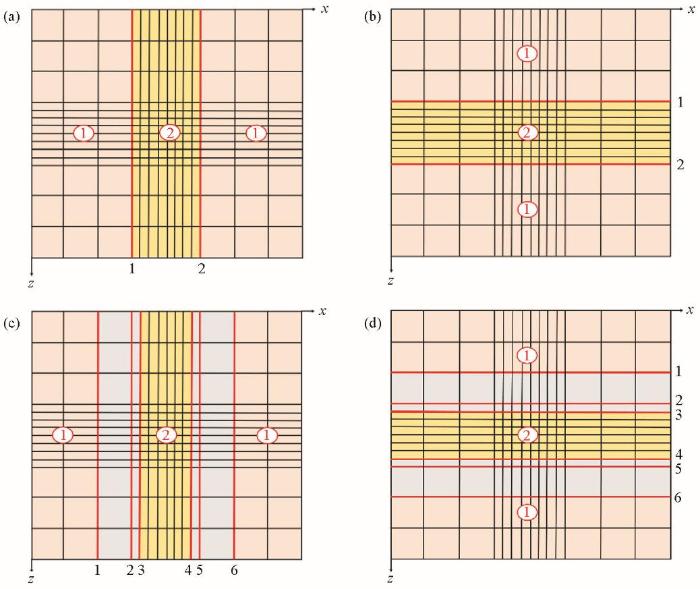
1)地震波旅行时对x方向的一阶差分格式如下: 图1a中区域①②内点的差分格式:
式中:当计算点在区域①时,dx=Δx;当计算点在区域②时,dx=Δx1。
图1a中红线1位置点的差分格式:
图1a中红线2位置点的差分格式:
2)地震波旅行时对x方向的二阶差分格式如下:
图1c中区域①②内点的差分格式:
式中:当计算点在区域①时,dx=Δx;当计算点在区域②时,dx=Δx1。
图1c中红线1位置点的差分格式:
图1c中红线2位置点的差分格式:
图1c中红线3位置点的差分格式:
图1c中红线4位置点的差分格式:
图1c中红线5位置点的差分格式:
图1c中红线6位置点的差分格式:
同理,地震波旅行时对z方向的一阶、二阶差分格式形式与x方向上的一致,用相同的方式求取即可。
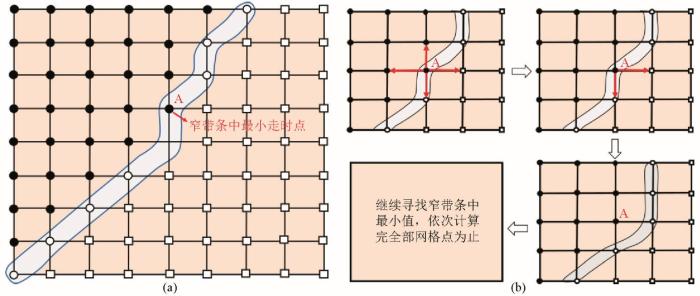
1.3 窄带技术原理
图2
2 正演模拟与精度分析
FMM计算地震波旅行时的精度主要受限于网格大小和差分格式阶数。由前人的研究发现在网格大小及差分格式阶数一定的情况下,地震波旅行时误差较大的区域主要来源于震源附近[10]。因此,本文采用变网格剖分形式,加密震源附近的网格密度,并通过正演模拟均匀模型,存在异常高速体模型及Marmousi模型,研究变网格FMM的优势及适用性。
2.1 均匀模型
建立二维均匀正演模型,模型的速度为2 000 m/s,垂直厚度为1 980 m,水平宽度为1 980 m,炮点设置在均匀模型的正中心(990 m,990 m)处,大网格剖分间距为12 m,小网格的剖分间距为4 m。采用常规一阶、二阶FMM、变网格一阶、二阶FMM、双重网格一阶FMM计算地震波旅行时,并且还分别考虑加角点及不加角点的情况。
图3
图3
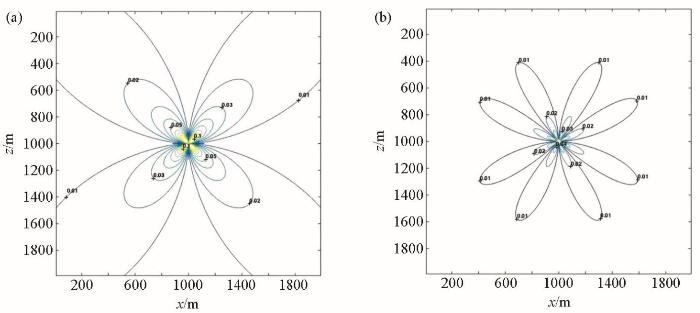
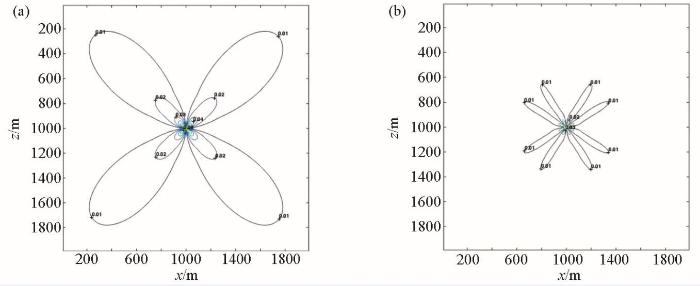
常规一阶FMM走时计算相对误差
a—不加角点;b—加角点;
Fig.3
Relative error calculated by conventional first-order FMM traveltime
a—no angular point;b—add angular point;
图4
图4
常规二阶FMM走时计算相对误差
Fig.4
Relative error calculated by conventional second-order FMM traveltime
图5
图5
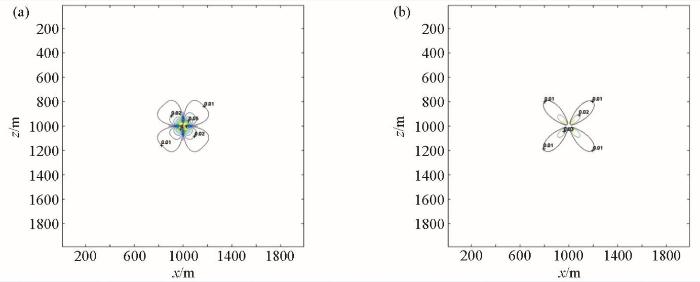
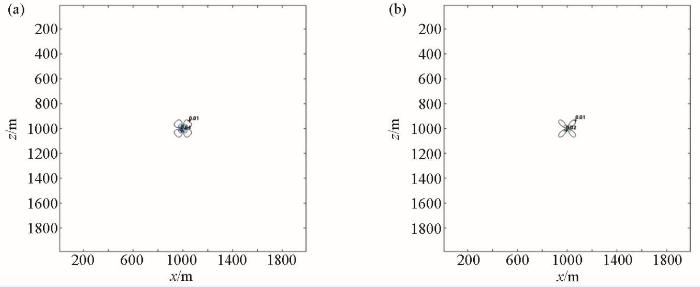
变网格一阶FMM走时计算相对误差
Fig.5
Relative error calculated by grid-variable first-order FMM traveltime
图6
图6
变网格二阶FMM走时计算相对误差
Fig.6
Relative error calculated by grid-variable second-order FMM traveltime
图7
图7
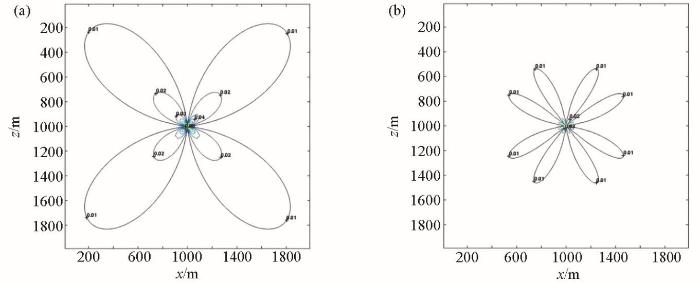
双重网格一阶FMM走时计算相对误差
Fig.7
Relative error calculated by double grid first-order FMM traveltime
表1 不同网格间距对应的网格点数
Table 1
| 网格类型 | 网格间距 | 网格点数 |
|---|---|---|
| 常规网格 | 12 m | 166×166(27556) |
| 常规网格 | 6 m | 331×331(109561) |
| 常网规格 | 4 m | 496×496(246016) |
| 常网规格 | 3 m | 661×661(436921) |
| 常规网格 | 2 m | 991×991(982081) |
| 变网格 | 大网12 m,小网6 m | 184×184(33856) |
| 变网格 | 大网12 m,小网4 m | 202×202(40894) |
| 变网格 | 大网12 m,小网3 m | 220×220(48400) |
| 变网格 | 大网12 m,小网2 m | 256×256(65536) |
| 双重网格 | 大网12 m,小网6 m | 28564 |
| 双重网格 | 大网12 m,小网4 m | 30220 |
| 双重网格 | 大网12 m,小网3 m | 32524 |
| 双重网格 | 大网12 m,小网2 m | 39076 |
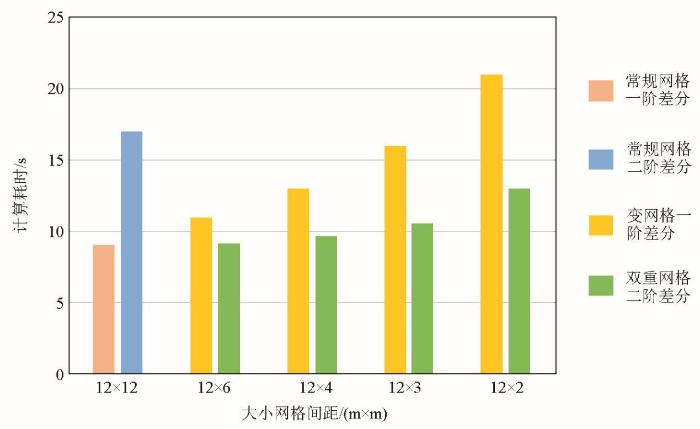
图8
图8
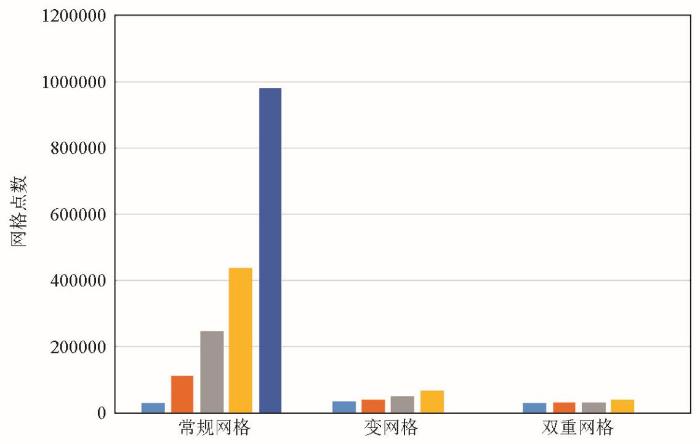
不同网格间距对应的网格点数
Fig.8
Number of grid points corresponding to different grid spacing
综上所述,在均匀模型背景下,综合考虑计算精度和效率,变网格FMM和双重网格FMM的优势相当;在保证计算精度和效率的情况下,为降低编程程序的复杂性,提高程序运行成功率,可考虑使用这两种方法的一阶差分代替常规FMM法的二阶差分。
图9
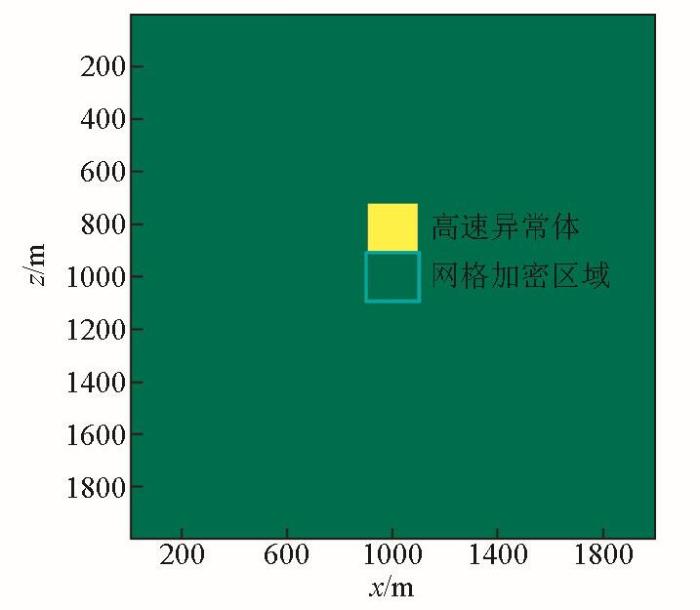
2.2 存在高速异常体模型
建立二维的、存在高速异常体的正演模型(如图10),模型的背景速度为2 000 m/s,垂直厚度为1 980 m,水平宽度为1 980 m。炮点设置在均匀模型的正中心(990 m,990 m)处,大网格剖分间距为12 m,小网格的剖分间距为4 m。高速异常体设置在震源的上方,与网格加密区域紧密相连,形状为正方形,厚为216 m,宽为216 m,速度设置在2 000~3 000 m/s范围内。采用变网格一阶FMM、双重网格FMM计算地震波旅行时,并分析旅行时对异常体的响应。与此同时,加密上述模型网格,使得网格间距全区域为2 m,采用常规二阶FMM计算旅行时作为该研究的对照时间(由图6可知,加密局部网格精度已接近解析解,说明加密全区域后计算出的旅行时作为解析解参照是可行的)。
图10
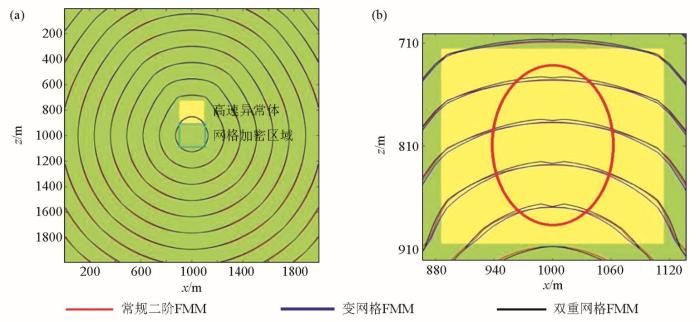
图11
图11
三种方法地震走时等时线
a—全区域;b—局部放大
Fig.11
Three methods isochronal line for traveltime
a—the whole area;b—fractionated gain
图12
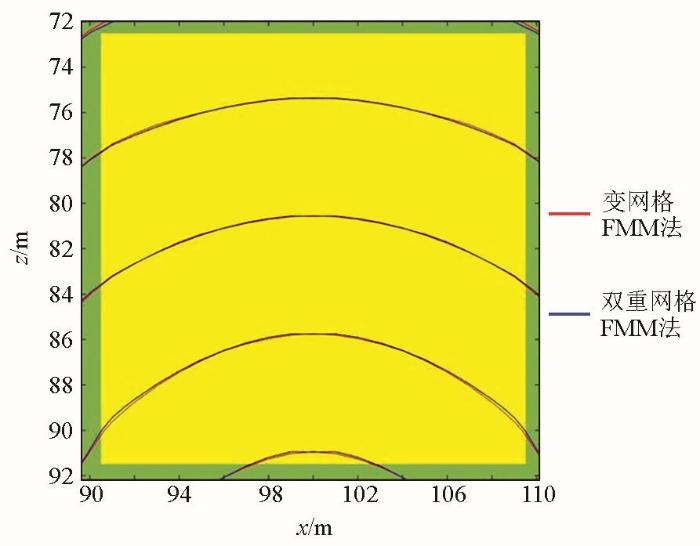
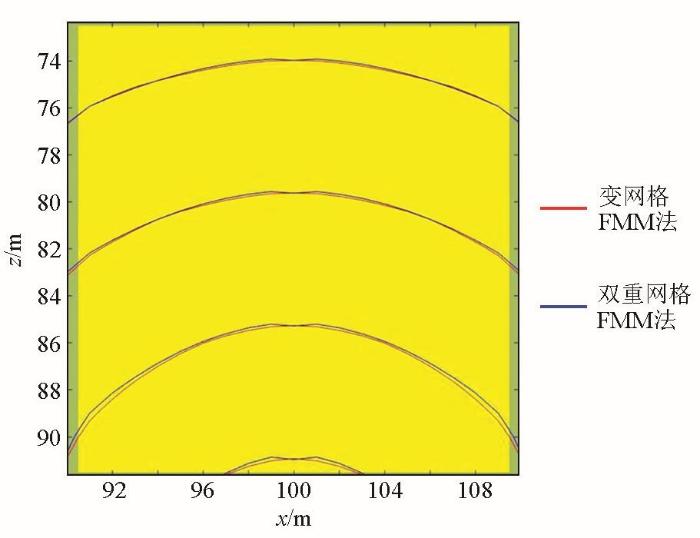
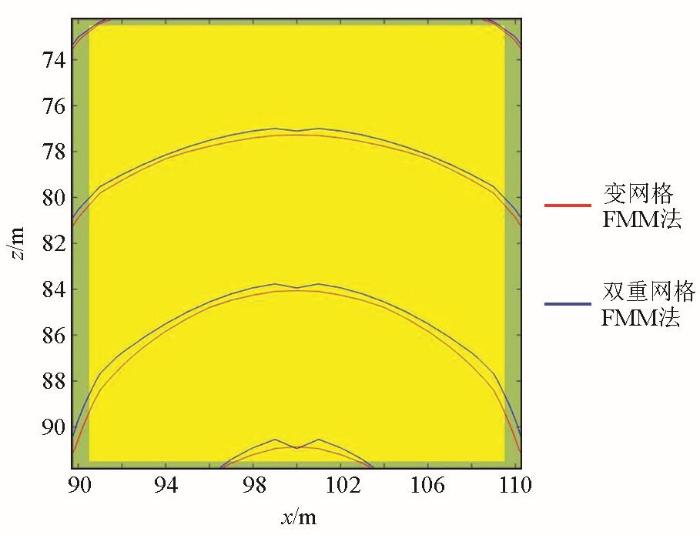
图13、14、15分别考虑异常体与围岩速度的差异,对两种网格剖分形式计算走时的影响,当异常体速度为2 300 m/s时,两种剖分形式计算走时相差不大,随着速度的不断增加,在异常体区域走时出现明显差异,由此可知,异常体与围岩差异速度越大,双重网格剖分形式计算走时误差越大。
图13
图14
图15
2.3 Marmousi模型
建立Marmousi模型,验证变网格FMM对复杂模型的适应性。Marmousi模型的区域范围为720 m×2 976 m,炮点设置在模型的底部(720 m,1488 m)处,大网格间距为6 m,小网格间距为2 m,小网格布置在震源附近。
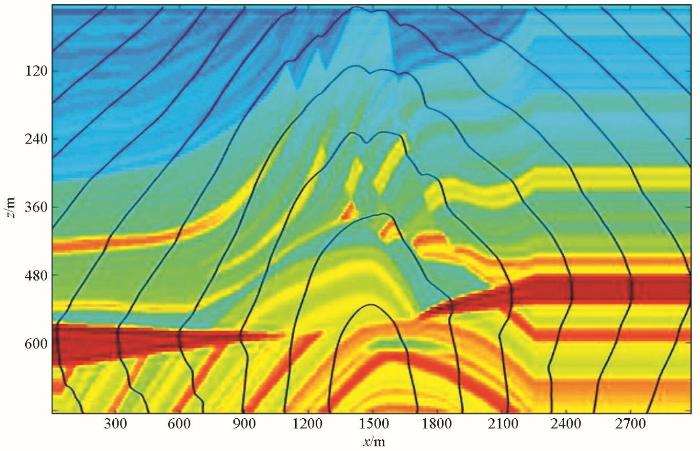
由图16可以看出,地震波波前总是寻找所需旅行时最小的路径传播,在高速异常区域,旅行时等时线向外凸出,而在低速异常区域,旅行时等时线向内凹进,这样的特征是符合地震波波前传播的规律的,说明采用变网格FMM计算地震走时是可行的,且能够适应各种复杂模型。
图16
3 结论与展望
通过对均匀模型、存在高速异常体模型、Marmousi模型正演模拟,得出以下结论:
1)对于均匀介质,变网格FMM和双重网格FMM优势相当,既有效降低计算精度,又大大提高计算效率。
2)对于存在高速异常体的介质,双重网格FMM需要考虑异常体与变网格的位置关系,否则双重网格FMM可能违背波前传播的规律,造成大的计算误差,而变网格FMM不需考虑这样的问题。
3)经Marmousi模型试算,变网格FMM对复杂模型的适应能力较强。
综上所述,变网格FMM用于计算地震旅行时,较常规网格剖分具有一定的优势,不仅能提高计算精度,也能提高计算效率。另外,变网格FMM还有较大的研究空间,除对震源区域采用小网格剖分外,还可以考虑对速度梯度变化较大的区域进行小网格剖分,从而提高复杂模型的成像精度;还可以将固定形式的变网格直接改进为自适应形式的变网格,对全区误差大于阀值的区域进行网格加密,进一步提高旅行时计算的精度。
参考文献
基于快速推进法的三维随机介质地震波走时计算
[D].
The calculation of seismic traveltime based on FMM in 3-D random medium
[D].
Minimum traveltime tree algorithm for seismic ray tracing:improvement in efficieney
[J].
Finite-difference calculations of traveltimes
[J].
一种新的基于多模板快速推进算法和最速下降法的射线追踪方法
[J].本文提出了一种新的射线追踪方法,该方法将射线追踪分为两个过程:首先使用多模板快速推进算法(MSFM)从源点开始计算已知速度场各网格节点的波前传播时间;然后使用最速下降方法从接收点开始向源点沿旅行时梯度最快下降方向追踪射线路径.与传统的快速推进方法(FMM)及其改进算法相比,多模板快速推进算法(MSFM)使用两个模板计算邻点旅行时,同时考虑了水平、垂直及对角线方向上的信息,能大大提高旅行时的计算精度和计算效率.为了验证新射线追踪方法的计算精度和计算效率,本文对两个速度模型进行了数值模拟,并将模拟结果与基于FMM和高精度快速推进方法(HAFMM)的最速下降射线追踪方法计算结果进行对比.对比结果表明,本文方法是一种有效的射线追踪方法,并且在计算精度和计算效率上都优于基于FMM和HAFMM的射线追踪方法.
A new ray tracing approach based on both multistencils fast marching and the steepest descent
[J].
3-D traveltime computation using the fast marching method
[J].DOI:10.1190/1.1444558 URL [本文引用: 1]
快速推进法计算精度分析及改进
[J].
DOI:10.3969/j.issn.1672-7940.2009.03.001
URL
[本文引用: 1]

讨论了差分格式,网格间距,速度等因素对快速推进算法(FMM)计算精度的影响。对均匀模型的计算表明,在网格间距不变的情况下,一阶差分格式的计算误差明显大于二阶差分格式计算误差;在差分格式不变的情况下,网格间距越大,误差越大,二者基本成线性对应关系。速度和误差分布也近似成对应的线性关系。提出了对炮点周围网格进行局部精细处理,可以获得全局上的更高计算精度的处理方法。数值实验表明,在同样差分格式和网格间距下,该方法可以获得较以前方法数倍以上的精度。另外,在保证精度的前提下,采用该方法,可以加大网格间距,从而提高了计算效率。
Analysis on calculation accuracy of fast marching method and its improvement
[J].
Multiple reflection and transmission phases in complex layered media using a multistage fast marching method
[J].DOI:10.1190/1.1801950 URL [本文引用: 1]
FMM射线追踪方法在地震学正演和反演中的应用
[J].
DOI:10.3969/j.issn.1004-2903.2010.04.008
URL
Magsci
[本文引用: 1]

FMM(Fast Marching Method)射线追踪方法是一种求解非线性程函方程数值解的射线追踪方法.本文在FMM射线追踪算法流程的基础上引入一个数据链表,方便求解射线路径,另外还引入一个与解精度有关的方向参数,可以更好的控制解的精度.然后在一些理论模型中对FMM方法的正演和反演计算做了若干验证,结果表明,FMM方法可以较快而且稳定地得到令人满意的结果.
Application of FMM ray tracing to forward and inverse problems of seismology
[J].
复杂地表条件下地震波走时计算方法研究
[D].
Study on the computation method of seismic traveltimes including surface topography
[D].
快速行进法射线追踪提高旅行时计算精度和效率的改进措施
[J].
DOI:10.13810/j.cnki.issn.1000-7210.2016.03.007
URL
Magsci
[本文引用: 1]

快速行进法(FMM)是一种基于网格的新型射线追踪方法,其旅行时计算精度和效率受差分格式及网格剖分大小的影响。本文针对传统FMM旅行时的精度和效率存在的问题,给出三项改进措施: ①加入角点计算; ②细化并补充改进一阶差分计算公式; ③引入Vidale差分方法,并采用双重网格技术与三者结合。模型试算结果表明:第一项改进措施可提高一阶差分格式及其计算精度,后两项改进措施可不同程度地提高FMM旅行时计算的精度和效率,增强了FMM的适用性,有利于基于网格的射线追踪法的应用。
Improved fast marching method for higher calculation accuracy and efficiency of traveltime
[J].
针对复杂地形的三种地震波走时算法及对比
[J].
DOI:10.6038/j.issn.0001-5733.2012.02.018
Magsci
[本文引用: 1]

复杂地形条件下地震波走时算法对于研究复杂地形地区的成像问题有着重要的意义.为了得到精度高且适应于复杂地形的走时算法,首先提出阶梯网格迎风差分法.然后将该方法与不等距网格有限差分法和混合网格线性插值法进行对比研究,得出如下结论:混合网格线性插值法的计算精度最高,但其计算效率最低;阶梯网格迎风差分法的计算精度最低,但其计算效率最高;不等距网格有限差分法的计算精度和计算效率均居中;而究竟选取哪种算法作为给定复杂地形模型的地震波走时算法,应该综合考虑地形的特点、所研究问题对计算精度及计算效率的要求等因素.最后通过一个计算实例验证了三种算法在面对复杂地形、近地表及地下复杂介质等复杂地质条件时均有很好的适应性和稳定性.
The comparison of three schemes for computing seismic wave traveltimes in complex topographical conditions
[J].
变网格有限差分弹性波方程数值模拟方法
[J].
DOI:10.3321/j.issn:1000-7210.2007.06.006
URL
[本文引用: 1]

研究复杂介质中地震波传播规律及地震响应特征,需要在细小网格剖分下进行弹性波方程数值模拟计算,而小网格下的数值模拟计算将带来巨大的计算量问题,采用变网格计算是减少计算量的有效途径。本文给出一种变网格差分计算的实现方法,在局部复杂介质区域采用细网格计算,其余区域采用粗网格计算,在两种网格的过渡区通过改变差分算子和波场插值实现波传播的过渡衔接。理论分析和数值模拟结果表明,变网格时在粗细网格的过渡区不会对地震波传播模拟带来影响,从而达到了既减少计算量又保证计算精度的目的。
Numeric simulation by grid various finite difference elastic wave equation
[J].
步长自适应的有限差分复杂地表波场数值模拟
[J].复杂地表条件下的有限差分地震波场的数值模拟,由于受到低速层和地表起伏的限制,模型速度分布范围变大,一般使用精细的差分网格来抑制频散,提高模拟分辨率,但精细网格会显著增加计算成本.为了能有效地解决这一问题,本文提出一种步长自适应有限差分波动方程数值模拟方法.(1)新方法根据模型中的介质速度分布,对不同的速度区域采用与该速度匹配的空间步长,实现对模型空间网格的步长自适应精细划分.对于速度分布范围大的复杂地表模型,新方法不仅能够极大地减少模型的网格节点数,同时又能提高波场的时间采样步长,减少时间采样数,提高计算效率.(2)推导了不同步长边界网格节点Laplace算子的二阶有限差分表达式,避免了在这些结点进行插值计算产生的假扰动和数值不稳定问题.(3)为了降低有限差分产生的数值频散,本文在常规的差分方程中增加了一频散校正项,能有效地衰减了高波数成分,抑制了数值频散.对复杂近地表的波场数值模拟结果表明,本文提出的步长自适应新方法能够有效减少网格节点数和时间采样数,极大地提高计算效率,计算量比常规粗网格增加一些,但效果能够达到了常规精细网格的模拟结果.
Seismic wave simulation method based on variable grid step
[J].
一阶弹性波方程的变网格高阶有限差分数值模拟
[J].
DOI:10.3321/j.issn:1000-7210.2008.06.017
URL
Magsci
[本文引用: 1]

使用可变网格的有限差分法进行地震模拟有许多独特的优点,主要表现为对地质模型的离散化更为合理,在低速带和复杂构造区域,可将局部网格划分得相对精细些,不仅提高了模拟精度,消除了因采样不足导致的频散现象,而且可以减少计算机内存需求,保持模型计算的灵活性。本文提出一种新的基于高阶交错网格技术的弹性波数值模拟方法,通过改变网格的空间步长实现了局部网格加密技术,弥补了常规网格的缺陷和不足。试算结果表明,本文提出的算法稳定性较好,且能够提高模拟精度,减少计算时间,提高计算效率。
Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation
[J].