随着世界经济发展对能源需求量的增加以及石油天然气勘探开采难度的提高,传统的高孔隙、高渗透率油层大多已经被勘探开发,这就对石油天然气的继续勘探开发提出了更高的要求^[1]。在岩石物理、电法测井等领域,对储层岩石等效电学参数的研究有助于判断地下油气储藏分布和鉴别油水层,其中岩石的等效电导率(或电阻率)及等效介电常数是测井应用中关注的主要电学参数^[2,3],常用的获取方法包括建立不同理论模型和数值及实验分析方法,由于建立的解析或经验模型大多针对特定理想结构,在分析具有任意复杂微观结构的天然岩石样本时具有局限性;在实验测量分析方面,近些年较为主流的岩石等效电学参数测量方法包括井中测量和实验室取芯测量,由于井中测量难度较大,经济成本较高,大多数岩石分析工作选择从井中取芯后进行样本加工处理,然后利用实验室设备进行测量。实验室测量对岩石样本加工要求较高,且样本的可重复利用率也较低。

近些年,数字岩心技术作为一种新兴前沿的岩石特性分析方法,具有成本低、时间短、精度高、可重复等特点^[4,5]。采用数字岩心计算岩石混合介质等效电学参数近年来引起了国内外广泛关注。澳大利亚国立大学(australia national university)的Mark A Knackstedt等^[6,7]针对石油地质领域的应用研究提出数字岩心(digital core)的概念并进行了一些研究工作;长江大学的朱伟等^[8]通过数字方法与成像技术相结合,建立数字岩心模型并进行物理场数值模拟及等效物理参数的计算,研究岩石微观结构、物质组成与宏观等效性质之间的关系;中国石油大学的杨永飞等^[9]提出一种利用电镜扫描方法获取岩样的扫描图像,根据图像处理和马尔科夫链法重构出相应的无机孔隙数字岩心、有机孔隙数字岩心和基质孔隙数字岩心的结果的方法;核工业二一六大队的张强等^[10]以二维岩心图像的微观孔隙结构特征建立三维数字岩心模型,并采用有限元法模拟所建岩心模型的等效电学参数。

笔者利用CT或扫描电镜(SEM)分层扫描岩石样本获得图像数据,借助图像处理方法对样本数据进行三维重建、矿物分析、孔隙度判定等,继而建立精确的数字岩心模型,并利用数值计算软件对岩石样本物理参数进行计算分析。这一套针对岩石样本图像处理、三维重构以及等效电学参数的仿真计算等方面开展研究的方法,将对利用岩石电学特性进行测井解释、储层评价及储量预测等领域提供重要的理论意义和实际价值。

笔者研究的岩石等效电学参数是岩石的混合介电常数,岩石是由多种介质组成的混合物质,因此岩石的介电常数属于混合介电常数,混合介电常数的大小在外界条件相同的前提下取决于混合物的组成部分、所占比重以及分布情况,岩石的混合介电常数为^[11]:

其中:ε代表混合物质的介电常数,D代表闭合曲面的电位移矢量,E代表闭合曲面的电场值,ε_s是岩石骨架的介电常数,ε_p是岩石孔隙的介电常数,E_p是岩石骨架的电场强度,E_p是岩石孔隙的电场强度。

准确计算岩石混合介电常数需要精确地分辨出岩石的骨架和孔隙,这就要求准确地对岩石样本进行图像分割及建立无损三维数字仿真模型。

岩心样本为已知测量参数的砂岩a,砂岩b,页岩a及页岩b4种岩石样本,借助蔡司Xradia 520CT扫描仪进行无损扫描,获得岩心样本的CT断层扫描序列。对砂岩样本a局部(region of interest, ROI)进行扫描,其分辨率为2 um,ROI尺寸为直径约2.05 mm,长度约2.05 mm的圆柱体样本,可获取到1 001张992×1 015像素的二维CT切片图;页岩样本a的分辨率为0.7 um^[2],ROI尺寸为直径约 7.17 mm,长度约7.17 mm,可得到994张984×1 015像素的二维CT切片图。每种岩石样本的CT切片如图1所示。

由于岩心CT图像的灰度值表征岩心内部各成分在空间的分布,其可以代表岩心的骨架和孔隙,针对CT成像的原理发现CT扫描图像存在不可避免的噪声,采取图像滤波去除CT断层图像的噪声,分析不同岩石样本的灰度直方图分布类型确定对应的图像分割算法,准确分辨出岩心的骨架与孔隙。

噪声虽然不可避免,但是噪声的产生概率一般符合某种数学模型。按照图像产生过程中噪声的概率密度规律不同,可分为高斯噪声、伽马噪声、瑞利噪声、指数分布噪声以及脉冲分布噪声等模型。想要有效地消除图像存在的噪声,就必须分析噪声的模型^[12]。

相关研究发现,当X射线的量子统计噪声为主要噪声时,噪声的标准差σ_d满足表达式:

其中:μ_b( E̅)表示圆柱体物质对能量为 E̅的X射线衰减系数,R表示圆柱体物质的半径。采集数据过程中,量子统计噪声满足泊松分布,而对于多次独立采集的组合,可近似地认为其服从正态分布,其表达式如下:

其中:P(μ)为衰减系数μ的概率分布^[13]。由以上分析可知,CT图像的噪声主要符合正态分布,即为高斯噪声。

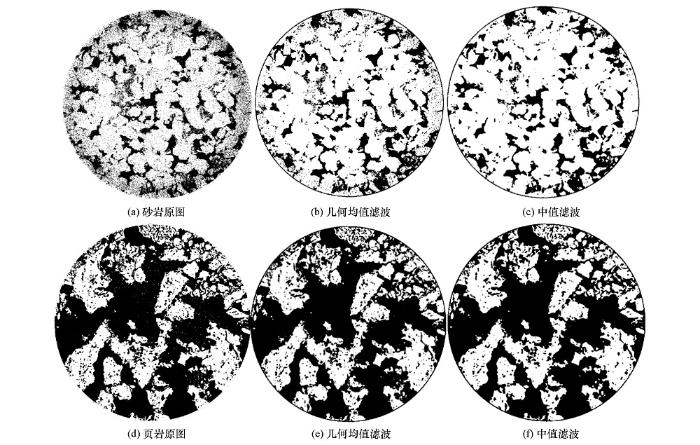
通过分析CT图像的噪声类型,单单采用一种滤波方法是无法彻底滤除噪声的,因此在几何滤波的基础上再进行中值滤波处理,其效果如图2所示。

两种岩石样本经过几何均值滤波以及中值滤波处理后,上述分析的高斯噪声以及椒盐噪声已经基本消除,这一步为处理岩石图像的预处理部分,这一步的完成情况直接决定了后边对岩石孔隙度、电导率以及混合介电常数计算结果的准确度,因此这一步是进行数字图像处理中必不可少的一步。

鉴于CT扫描的岩石样本图像存在固有的特征,即物质的密度由像素灰度值表示,在图像分割过程中常采用灰度阈值分割的方法。阈值分割的本质是根据图像的灰度分布,以适当的准则选取阈值将图像进行分割。对于岩石样本CT扫描图像f(x, y)(其背景灰度值为0),经过阈值T进行处理后,可以得到图像g(x,y)为一个二值化的图像:

被标记为1的像素代表的是岩石骨架,被标记为0的像素代表的是岩石孔隙,T表示阈值。

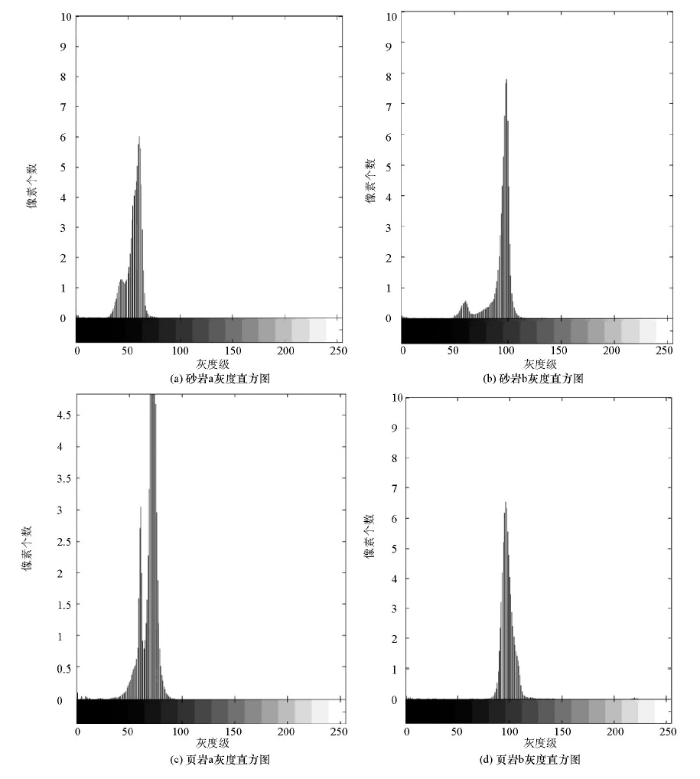
采用灰度阈值分割的方法对岩心图像进行处理,图3所示为各样本的灰度直方图。可以发现:砂岩a、砂岩b、页岩a的灰度直方图为单峰模型,页岩b的灰度直方图为双峰模型,说明对于不同类型的灰度分布如果采用同一种方法进行分割,将导致其中某种类型的计算结果出现偏差。因此,笔者针对不同的模型采用不同的分割方法以求最大限度提高数值计算的准确性。

2.2.1 单峰模型阈值分割方法

通过观察单峰模型可以发现样本的灰度图像分布曲线类似于正态分布曲线,这与形成岩石的地质作用有着密切的关系,也从侧面印证了岩石在漫长的形成过程中,其内部的成分分布是满足某种概率分布的。在数字图像处理中,对于这种模型一般采用最大类间方差法的分割准则对其进行处理。

现假设某一阈值T将图像分为C₁(I₀≤I_i≤T)和C₂(T≤I_i≤I_L-1) 两部分,则这两部分出现的概率w₁和w₂分别为:

而C₁和C₂两部分的均值μ₁和μ₂分别为:

其中计算的图像灰度均值μ可用部分均值μ₁和μ₂表示,表达式为:

由以上计算的参量可以计算出图像f(x,y)经过阈值T分割后的类间方差σ²为:

由上式可以发现,σ²是一个关于阈值T的函数,选取满足σ²最大的阈值T₀为满足最大类间方差准则的最佳阈值。

虽然最大类间方差准则^[14]广泛应用于基于阈值的图像分割中,但是当图像的目标信息与背景所占的比例极其不平衡时,例如岩石样本孔隙度小于10%时,孔隙占比远远小于骨架的占比,这种情况下为保证方差最大往往会导致阈值的失真。说明最大类间方差法得到的阈值导致计算的岩石孔隙度偏大,因此在实际应用中通常需要对类间方差法进行改进。

笔者提出缩小ROI区域到灰度值小于均值的左侧,并以缩小后的ROI的灰度均值μ作为上界,通过分析上述6种岩石样本可以发现,当阈值为缩小后ROI的灰度均值时,计算的孔隙度约为30%,远远大于这些岩石样本的实际孔隙度,因此针对这些岩石样本进行改进方法,以缩小后ROI 的均值μ作为上界,步进值为1进行遍历计算不同阈值的方差,并进行比较确定使得方差最大的最佳阈值。阈值T的表达式为:

改进后的最大类间方差法,其具体步骤如下:

1)计算岩石样本CT扫描图像的灰度均值,取灰度均值左侧的部分作为缩小后的ROI区域;

2) 统计ROI灰度分布,确定灰度值向量 A̅,计算ROI区域的均值μ,并取初始阈值为T=μ-α,α=1,将灰度向量 A̅分割为两部分,分别为向量 A1¯(A<T)和 A2¯(A≥T);

3)计算向量 A1¯(A<T)和 A2¯(A≥T)的类间方差σ²并记录于矩阵中;

4)将α的值加1,重复步骤2和步骤3,直至T<1;

5)比较矩阵中所有的类间方差,确定类间方差值最大时所对应的阈值为最佳阈值T₀。

2.2.2 双峰模型阈值分割方法

岩石由孔隙与骨架两部分组成,孔隙位于低灰度值部分,骨架位于高灰度值部分,相对于某一最佳分割阈值,孔隙与骨架相当于两个独立的部分,而因为其像素个数之间的差异会产生悬殊较大的峰值,一般大峰代表骨架部分,小峰代表孔隙部分,当孔隙为大尺度孔隙或孔隙尺寸分布较集中时,岩石的双峰性表现较为明显^[15]。用g₁,g₂分别表示岩石样本灰度图的最高峰和第二高峰(简称为小峰)所对应的灰度值,T表示岩石样本的理想分割阈值,则这三者的关系见表1(保留一位小数)。

设定两个参变量λ(大峰的权重)和τ (小峰的权重),使得:

其中:λ+τ=1,λ和τ均为正数,g₁代表大峰的灰度值,g₂代表小峰的灰度值。

根据双峰之间所占权重的变化确定分割阈值,并以最大熵阈值法作为分割判定条件,得到双峰模型的最佳分割阈值。最大熵阈值法^[4]是一种基于信息论中最大熵准则的图像阈值自动选取方法。这种方法的基本思想是对特定区域内的阈值进行遍历判断,找到最佳阈值使分割后的目标和背景的熵总值最大,或使分割后图像的目标与背景两部分的信息量最大。由式7、式8得到图像的总像素M以及每个灰度值出现的频率P_i,定义孔隙熵和骨架熵分别为:

其中: PT=∑i=1TPi,使得熵值

当H_T(T)取得最大时,所对应的阈值即为最佳阈值t:

2.2.3 不同分布类型的图像分割结果比较

利用上述两种方法对单峰及双峰模型分别进行图像分割确定最佳分割阈值并据此计算样本的孔隙度,表2所示为4种岩石样本的孔隙度结果比较,通过与实际岩石孔隙度进行比较,其相对误差保持在5%左右,分割效果较好,为下一步准确计算实际岩石等效电学参数提供保证。

目前,对于岩石等效电学参数的测量,主流的实验测量法有谐振腔法、同轴线法和电容法等。对于以上方法的缺点是都需要特定尺寸的实际岩石样本,这就造成岩石样本的浪费,不利于样本的二次利用。基于数字化岩心技术计算岩石的等效电学参数可以实现岩石样本的多次利用,这就需要对岩石样本进行岩石三维数值模型构建,通过建立与实际岩石样本内部结构一致的三维数值模型,并在电磁仿真软件中仿真计算得到岩石的等效电学参数。

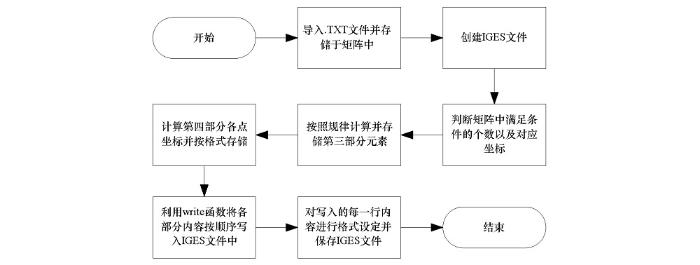
笔者采用基于有限元(FEM)的三维电磁仿真软件HFSS作为仿真计算岩石等效电学参数的工具。由于岩石是由骨架和孔隙两部分组成,因此三维岩石数值模型的建立是根据上节中确定的最佳图像分割阈值,将二维图像二值化为孔隙和骨架两部分,并将存有岩石骨架和孔隙的矩阵信息导出为.txt文件,通过Fortran软件编写一种可直接导入到HFSS的图形文件,在HFSS中的modeler按键下存在导入和导出功能,该功能支持HFSS中模型的导入导出,所以只需要将矩阵信息按照一定条件编写成HFSS可以识别的文件格式即可导入到HFSS中,通过比较各种格式文件内容、编写难度和导入的速度,最终选择IGES格式作为导入文件的格式。图4所示为利用Fortran生成IGES文件的程序设计流程。

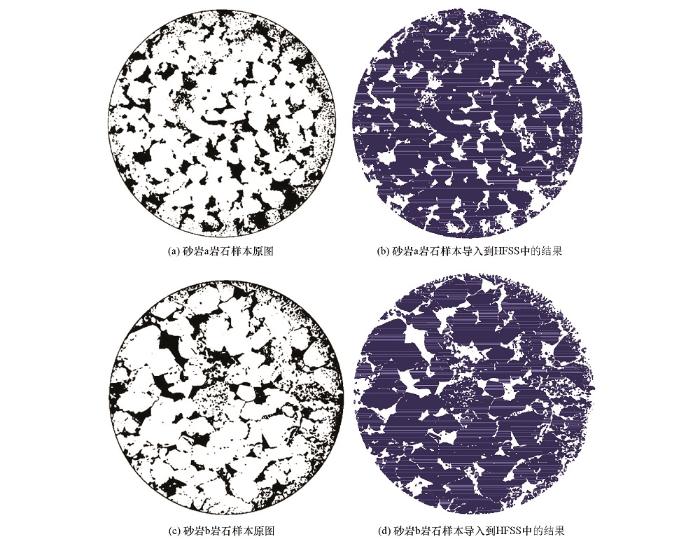
HFSS对于仿真模型需要进行设置材料处理,而生成的二维平面模型无法设置材料,因此三维岩石数值模型中的每个像素点按照岩石实际尺寸对应一个六面体模型,由于岩石样本对应的像素点数庞大,导致生成的六面体模型个数也非常多,为了提高仿真计算的效率需要对程序进行优化,对模型进行按行按列同类型合并的处理,可以极大的减少模型数量并提高仿真速度。图5所示为合并处理后岩石样本原图与IGES文件导入到HFSS中结果图比较。

由于目前对模型的优化有限,无法将岩石整个模型进行还原,因此构建多层局部三维数字模型进行仿真计算,岩石样本局部三维数字模型如图6所示^[3]。

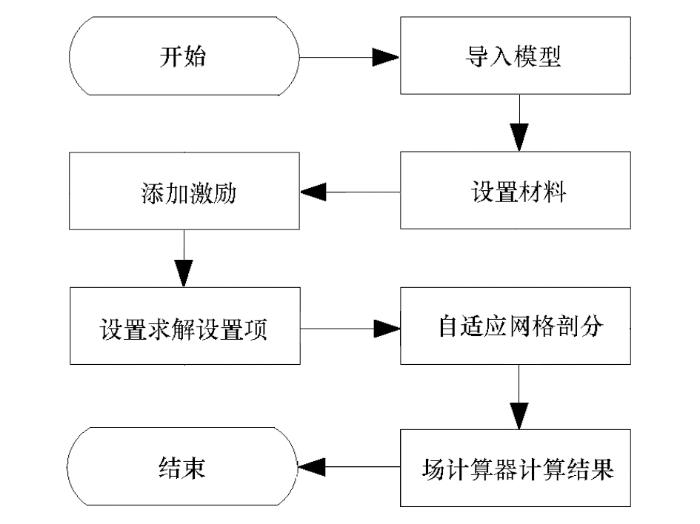
利用仿真方法计算岩石的等效电学参数主要是基于数字岩心技术,通过CT扫描的岩石样本二维CT图像,采用图像处理的方式对二维图像进行预处理滤波以及图像分割并将二值化后的图像信息导出为.txt文件,利用此文件构建三维岩石数值模型,将存有岩石样本的.txt文件转换成可在电磁仿真软件HFSS中进行仿真的图形结果模型,根据岩石样本本身的骨架和孔隙信息设置相应的材料特性,并对整个模型模拟添加激励以及求解设置项,最后利用HFSS自带的场计算器对仿真结果进行计算,求解得到岩石的等效电学参数。利用HFSS仿真计算岩石等效电学参数的流程如图7所示。

由于HFSS可以运行脚本文件,因此设置材料、添加激励和设置求解设置项可在脚本中一次设定,对于场计算器中由于岩石模型包含多个六面体,计算需要重复性操作多次,因此为了提高效率可以编写脚本利用循环语句进行计算。

通过上述流程计算岩石的等效电学参数并与许文博提出的岩石等效电学参数自动化测量系统^[16]测量结果进行比较。表3所示为笔者提出的仿真计算等效电学参数的方法及自动化测量系统测量的结果比较。

基于数字岩心技术,通过对岩石断层图像进行预处理、阈值分割、三维岩石数值模型的建立,HFSS仿真计算等一整套方法计算得到岩石的等效电学参数,其计算结果与实验测量结果吻合度较高,但是相较于实验测量,数值仿真计算可以避免制作岩石样品的复杂步骤,并且可以避免外界环境对于测量结果的影响。为计算岩石微观结构的等效电学参数提供了一种有效的方法。这一套针对扫描岩心图像的数据处理、数值模型转换以及电磁参数计算方法可应用于高效、精确分析不同类型数字岩心的介电常数、电导率等电磁学特性,可为岩石物理、测井解释、储层评价等领域提供重要的参考依据。