0 引言
在陆地地震勘探数据中,近地表异质性和地表散射衰减了有效反射信号,增加了记录信号的复杂度。通常情况下,在地震数据应用中近地表散射波被看作是一个极具干扰的噪声源,但在照明不足情况下其增加了地下照明度
地震数值模拟的方法已被广泛应用于研究非均匀介质中的波传播问题。一些学者基于扰动理论和Born近似研究了弹性波散射的正演[3,4,5]和反演[6,7]问题。这些方法在处理不适合一次散射(Born)近似的复杂异质性介质时具有局限性。有限差分算法模拟弹性波传播[8,9,10,11,12,13]并处理不规则自由表面边界条件[14,15,16,17]已经在文献中广泛讨论,其可以处理复杂背景介质以及不规则起伏界面。为解决近地表散射体成像问题,基于求解积分方程[18,19]的成像方法应运而生,但这些方法局限于散射体弱异质性情况,基于双程波动方程的逆时偏移[20,21,22]成像方法可以对任意波进行成像(包括回转波、棱柱波、转换波等),并能解决复杂构造的成像问题。虽然基于声波方程的逆时偏移比弹性波逆时偏移应用更广泛,但地下介质是弹性的,实际野外记录包括P波、S波以及转换波。这促使更多学者利用弹性波逆时偏移研究转换波模式下的成像问题。Sun[23]等利用标量波动方程进行波场外推,并将波场分离为PP波、PS波,实现了波场分离的弹性波逆时偏移。
文中选择有限差分算法模拟浅地表散射体的多重散射与地表之间的相互作用,基于扰动理论[21]分离散射波场与总波场。首先分析了近地表散射体的波场特征及其对地震面波、反射波的影响;随后提出散射波逆时偏移成像方法利用分离的散射波场对散射体成像。总结了近地表散射波的基本性质和形态特征及其在近地表速度反演、成像领域的可利用性。
1 基本理论
1.1 近地表散射波场数值模拟
在均匀各向同性弹性介质中波动方程为:
其中u为弹性波场,F为震源项,λ, μ为拉梅常数,ρ为介质密度。
在非均匀介质中,扰动理论[24]认为散射介质是一种密度和速度扰动,介质参数可分解为背景部分和扰动部分:
式中λ0(x, z)、μ0(x, z)、ρ0(x, z)为背景介质参数,δλ(x, z)、δμ(x, z)、δρ(x, z)为扰动介质参数。u0、us分别表示背景场和扰动场,在背景介质中u0满足:
考虑非均匀介质中总波场u可分解为背景场u0与散射场us两部分,即:
将式(2)~(4)代入式(1)中,可以得到散射场与总波场之间的关系:
方程(5)的左端描述了散射场在背景介质中的传播过程,其包括一次散射和多次散射;右端则等价于非均匀体与波场相互作用引起的等效体力,其取决于扰动介质参数和非均匀介质的格林函数。然而根据扰动理论[24]直接求解方程(5)存在着诸如格林函数近似数值表达对波场求取不准确等问题。考虑到这方面原因,笔者根据方程(1)、(3)利用高阶有限差分方法分别模拟近地表散射介质中的总波场和背景波场,并根据方程(4)用总场减去背景场求取散射场。
1.1.1 高阶有限差分算子
二维各向同性弹性介质中,一阶速度—应力方程[25]为:
式中vx、vz分别为质点位移速度的水平分量和垂直分量;τxx、τzz分别为x和z方向的正应力;τxz为切应力;ρ为介质密度;λ和μ为拉梅常数。若横向网格间距为Δx,纵向网格间距为Δz,时间采样Δt,设x=iΔx, z=jΔz, t=kΔt,并记
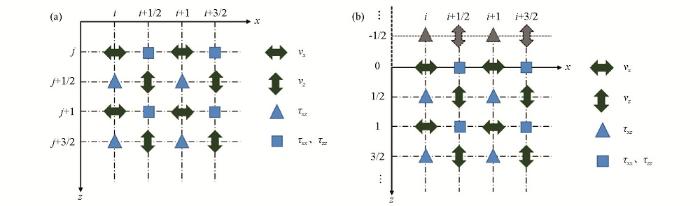
图1
其中,
1.1.2 水平自由地表边界条件
为了准确分析近地表散射波场(散射P波、S波、Rayleigh波)形态特征,必须设置更为合理的边界条件。在水平自由地表边界上,应力分量应满足[9]:
由于交错网格中不可能同时满足所有应力分量都在自由地表上,这里假定vx、τxx、τzz在自由表面上,如图1b,利用应力镜像法离散水平自由地表边界条件可表示为:
其中j=1、2、3、4(以空间八阶为例)。这样以满足应力在地表合力为零。
1.1.3 CFS-CPML吸收边界条件
其中,
其中复拉伸函数为:
所以式(6)频率域形式(限于篇幅这里以质点速度水平分量为例)可表示为:
为解决传统PML技术中在大炮检距掠射情况下吸收效果不佳现象,CFS-CPML技术引入了两个频移因子αx、αz和两个收缩因子kx、kz。此时,复频移拉伸函数sx、sz可表示为:
对比式(13)、(14),可见复拉伸函数是复频移拉伸函数在kx=1,αx=0情况下的特例。式(14)进一步整理可表示为:
将式(15)代入式(13)并变换到时间域可表示为:
其中:
为内部变量。沿x方向衰减因子dx,频移因子αx,收缩因子kx分别为:
其中,L为PML层厚度;x为计算网格点到PML层内界面的距离;d0、α0、k0为常数。z方向的参数与x方向相似。以上为波场计算时利用CFS-CPML技术处理边界过程,其不需要分裂波场,降低了数值误差,提高了计算效率。
1.1.4 稳定性条件
利用显式有限差分进行数值计算时,须考虑计算过程的稳定性,选取合适的空间网格大小和时间步长,能在保证计算精度的前提,兼顾计算效率。对于弹性波交错网格空间八阶差分显式的稳定性条件[29]为:
其中,Δt为时间步长;(vp)max为最大纵波速度;Δx、Δz分别为x、z方向网格间隔大小;
1.2 散射波逆时偏移
基于散射波逆时偏移的近地表散射体成像方法的主要思想是:从记录的总场中分离获得近地表散射波,并利用散射波进行波场逆时反传。主要步骤为:①波场正向传播,分离获取散射波场并作为震源波场;②震源波场逆时反传,记录检波波场;③分离获取震源波场、检波波场中的P波分量,利用零延迟互相关成像条件成像。成像条件可表示为:
2 数值实验
2.1 近地表散射体波场特征分析
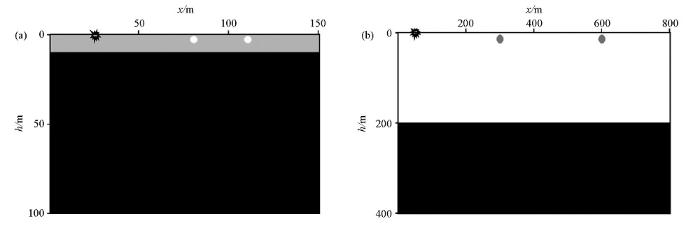
图2
表1 近地表散射体模型介质参数
| 模型 | 层厚(直径)/m | vp/(m/s) | vs/(m/s) | 密度/(kg/m3) | |
|---|---|---|---|---|---|
| 第1层 | 10 | 800 | 200 | 2000 | |
| 模型1 | 第2层 | 90 | 1200 | 600 | 2000 |
| 散射体 | 4 | 600 | 100 | 2000 | |
| 第1层 | 200 | 1800 | 1000 | 1750 | |
| 模型2 | 第2层 | 200 | 3000 | 1500 | 2250 |
| 散射体 | 20 | 2500 | 1200 | 2000 |
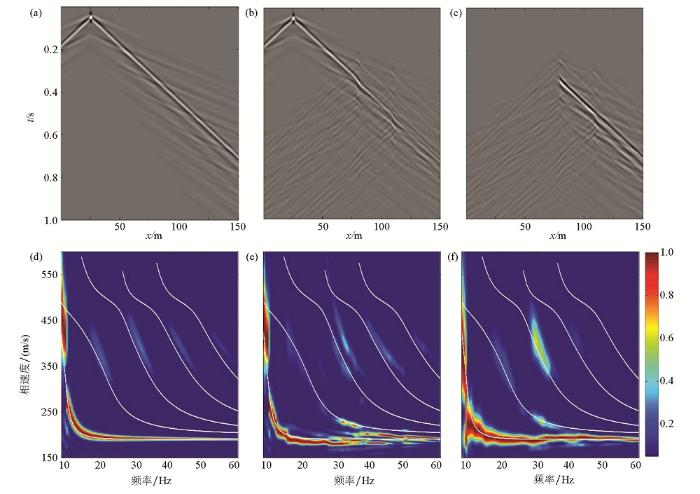
模型 1是研究Rayleigh波中散射波特征的速度模型,模型宽150 m、深100 m;散射体位置(z, x)分别为(3 m,80 m)、(3 m,110 m),散射体直径为4 m,如图2a所示,介质参数列于表1。正演模拟中,垂向和水平方向网格大小均为0.5 m,时间步长0.1 ms,采样间隔1 ms,记录时长1 s,子波主频25 Hz,震源位置(z, x)为(0.5 m,25 m)。采用时间2阶、空间8阶有限差分得到Rayleigh波记录(图3a~c),通过倾斜叠加算法[32]计算其对应的频散特征(图3d~f)。图3a~c分别为模拟介质不含散射体的背景场、含有散射体的总场、总场减去背景场的散射场。波场记录中高阶模式面波以及频散现象都很明显。图3d中背景场的各模式的频散特征与理论频散曲线吻合较好。图3e中总场的基阶、高阶模式能量均出现一定程度的不连续、分叉现象,但频散特征总体与理论频散曲线相近,并且在高阶模式能量上略强于背景场的高阶模式能量。图3f中散射场的基阶模式能量分布特征与理论频散曲线吻合度较高,第一高阶、第二高阶模式能量比背景场强。总体来看,散射波与面波混叠,总场、散射场的基阶模式能量都随着频率的增大,相速度逐渐减小并趋于表层横波速度200 m/s。散射体可以看作为一个二次震源,其在一定程度上增加了近地表的照明度,增加了高阶模式能量,为反演近地表速度提供了更多信息。
图3
图3
模型 1波场(垂直分量)模拟记录及其频散特征
a—背景场记录;b—总场记录;c—散射场记录;d—背景场频散特征;e—总场频散特征;f—散射场频散特征;频散图中的白色曲线为根据Haskell传递算法[33]正演所得的理论Rayleigh波频散曲线
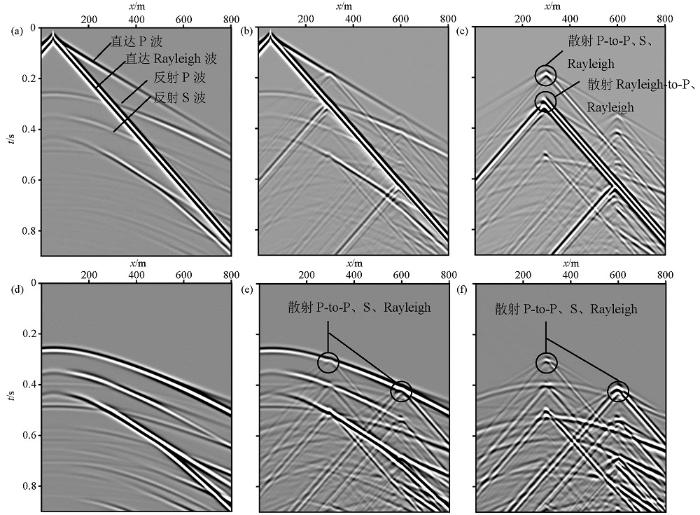
模型2是研究体波中散射波特征的速度模型,模型大小为宽800 m,深400 m;散射体位置(z, x)分别为(15 m,300 m)、(15 m,600 m),散射体直径为20 m,如图2b所示,介质参数列于表1。正演模拟中,垂向和水平方向网格大小均为1 m,时间步长0.1 ms,记录时长0.9 s,子波主频25 Hz,震源位置(z, x)为(1 m,50 m)。图4为波场模拟记录,图4a~c分别为背景场、总场、总场减去背景场的散射场;图4d~f为去除直达波的影响的背景场、总场、散射场。图4a记录中直达P波、Rayleigh波,反射P波、S波,转换波都很明显,Rayleigh波能量强于体波能量。图4c、4f为散射场,可以看出散射体处于近地表时散射波呈线性状,异于反射波的双曲状;面波散射(面波—面波、面波—体波)的能量相比体波散射(体波—体波、体波—面波)更强;正向散射能量强于逆向散射。图4b、4e总场中近地表散射波对有效反射信号的干扰是十分强的。由于散射面波能量较强,在近地表结构复杂区域散射面波可能掩盖主反射。了解近地表散射波的基本特征有利于开发合理的地震资料处理技术以提取、分离近地表散射波,提高地震资料信噪比。
图4
2.2 近地表散射体成像
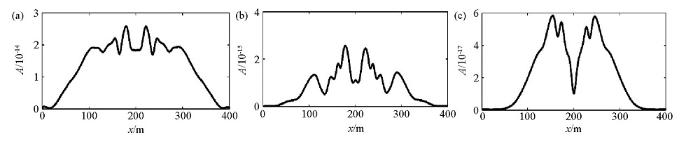
本节展示了散射波逆时偏移在近地表散射体成像中应用效果。散射波场是由总场与背景场的差值得到,将散射波场作为震源波场逆时反传,获得检波波场,最后提取震源波场和检波波场中P波分量利用成像条件得到成像剖面。首先分析单个散射体的成像效果,散射体直径10 m位于自由表面以下15 m深度处,模型参数列于表2,模型大小为横向400 m,纵向200 m,炮记录共40炮(起始炮点位置10 m,终止炮点位置400 m,炮间距为10 m),每炮共400道接收,道间距1 m,时间采样间隔1 ms,时间采样点数500,震源为35 Hz的Ricker子波。图5a为单个散射体的速度模型;图5b为总场逆时偏移成像结果,散射体轮廓刻画清晰、水平界面能量较均一;图5c为散射场逆时偏移成像结果,此时散射体轮廓刻画清晰,而水平界面同相轴相比图5b略差;图5d为不考虑自由地表条件下的散射场逆时偏移成像结果,散射场中只有散射体波—体波,不含有散射面波、散射体波—面波,此时散射体四周出现不收敛能量团。从上图可以看出逆时偏移可以对近地表弹性散射体精确成像。利用总场进行逆时偏移时,由于总场包含了一次反射波,水平界面同相轴能量更加均一。当利用散射波场逆时外推实现偏移时,虽然散射场没有包含炮点到水平界面的一次反射波信息,但包含了散射体(二次震源)到水平界面的反射信息,水平界面依然能成像,只是同相轴能量略微弱。假若不考虑自由地表边界条件,此时模拟的波场中不含有面波信息,散射场中就不含有散射面波、散射体波—面波,偏移成像结果中散射体边界的刻画出现不收敛能量团。提取水平界面均方根振幅如图6,可以看出,散射波场中包含了散射体到反射界面的反射信息时,能恢复部分水平界面能量,但散射波场中若不含有面波信息时,反射界面同相轴能量将减小一个数量级,甚至更多。从上面的分析不难看出,散射场中也包含了地层反射界面信息,在近地表勘探中,地震记录反射波信息缺失时,利用散射场结合逆时偏移对近地表散射体成像是可行的,并且散射波逆时偏移能有效利用近地表面波信息,使成像更加精确。
表2 近地表散射体模型介质参数
| 层厚(直径)/m | vp/(m/s) | vs/(m/s) | 密度/(kg/m3) | |
|---|---|---|---|---|
| 第1层 | 50 | 1800 | 1000 | 1750 |
| 第2层 | 150 | 3000 | 1500 | 2250 |
| 散射体 | 10 | 3000 | 1500 | 2250 |
图5
图6
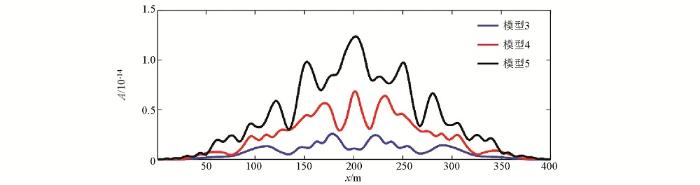
采用图5相同的散射体参数、正演参数和观测系统,分析不同散射体个数的散射波逆时偏移成像效果。图7成像结果中可以看出,所有的散射体均定位准确并精确成像。随着散射体个数增加,散射波中包含水平界面的信息越多,成像剖面中水平界面同相轴振幅增大(如图8)。浅部散射体增加了近地表照明度,即使检波器没有记录到炮点到界面的反射信息,利用近地表散射波也能对散射体附近构造成像。散射体波—面波沿着自由表面横向传播,增加了照明度,但由于面波衰减与深度呈指数函数关系,更接近于近地表散射体区域能更好地被散射波照亮和成像。在已知精确近地表速度场情况下利用散射波逆时偏移可以对散射体及其附近构造精确成像,若在实际近地表资料中未知精确的速度场,可以考虑引入反演思想的偏移方法结合散射波成像,例如最小二乘逆时偏移。
图7
图8
3 结论
笔者结合扰动理论和有限差分算法,分析了近地表散射波基本特征,提出了叠前散射波逆时偏移并应用到近地表散射体的成像中,数值结果表明:
1)近地表散射波呈线性状,异于反射波的双曲状;面波散射(面波—面波、面波—体波)的能量相比体波散射(体波—体波、体波—面波)更强;正向散射能量强于逆向散射。
2)一定尺度的近地表散射体可以看作是一个二次震源,增加了近地表的照明度;基于散射波的逆时偏移方法可以对近地表散射体精确定位和成像。
本文的分析和量化结果有助于解释散射机制, 有利于开发新的采集技术和数据处理方法,并利用散射波场特别是散射面波,提高近地表速度反演精度和地震成像精度。
参考文献
Imaging from multiply scattered waves
[C].
Increasing illumination and sensitivity of reverse‐time migration with internal multiples
[J].DOI:10.1111/gpr.2013.61.issue-5 URL
The Born approximation in the theory of the scattering of elastic waves by flaws
[J].DOI:10.1063/1.324142 URL [本文引用: 1]
Scattering characteristics of elastic waves by an elastic heterogeneity
[J].DOI:10.1190/1.1441934 URL [本文引用: 1]
Elastic ray-Born l 2-migration/inversion
[J].DOI:10.1111/gji.1989.97.issue-1 URL [本文引用: 1]
Removal of scattered guided waves from seismic data
[J].DOI:10.1190/1.1500386 URL [本文引用: 1]
P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method
[J].DOI:10.1190/1.1442147 URL [本文引用: 1]
Fourth-order finite-difference P-SV seismograms
[J].DOI:10.1190/1.1442422 URL [本文引用: 2]
Numerical modeling of elastic-wave scattering by near-surface heterogeneities
[J].DOI:10.1190/geo2013-0208.1 URL [本文引用: 1]
高阶交错网格有限差分法纵横波波场分离数值模拟
[J].
DOI:10.3969/j.issn.1004-2903.2010.03.021
Magsci
[本文引用: 1]

本文给出了一种等价的弹性波动方程,以解决完全弹性波场中不能完全分离耦合的纵横波波场问题.对该弹性波动方程进行公式换算,推导出新型等价一阶双曲型方程,应用高阶交错网格有限差分法求解该方程,并给出了相应的最佳匹配层(PML)吸收边界条件,对均匀介质模型、复杂Marmousi模型和实际地质模型进行波场分离数值试验,准确得到了混合波场、完全分离的纯纵横波波场.数值结果表明,本文方法具有比传统方法更好的数值模拟精度和边界吸收效果,同时分析分离后的纵横波纯波场,可观察到较为丰富的能量转换信息,并发现纯纵波场中的非均匀 平面波现象,该波为S波以临界角入射情况下的反射SP波,这对认识复杂弹性波的传播规律及弹性波理论具有重要意义.
A systematic and efficient method of computing normal modes for multilayered half-space
[J].DOI:10.1111/gji.1993.115.issue-2 URL [本文引用: 1]
A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography
[J].DOI:10.1190/1.1444107 URL [本文引用: 1]
Three-dimensional elastic scattering by near-surface heterogeneities
[J].DOI:10.1111/gji.2005.160.issue-2 URL [本文引用: 1]
Non-linear inversion of scattered seismic surface waves
[J].DOI:10.1111/j.1365-246X.2007.03557.x URL [本文引用: 1]
Reverse time migration
[J].DOI:10.1190/1.1441434 URL [本文引用: 1]
Migration by extrapolation of time-dependent boundary values
[J].DOI:10.1111/gpr.1983.31.issue-3 URL [本文引用: 2]
Iterative depth migration by backward time propagation
[C]//
Prestack scalar reverse-time depth migration of 3D elastic seismic data
[J].
The perturbation method in elastic wave scattering
[J].DOI:10.1007/BF00876266 URL [本文引用: 2]
弹性介质中瑞雷面波有限差分法正演模拟
[J].为研究瑞雷面波的形成机理及传播规律,促进瑞雷面波资料处理方法的发展,本文根据弹性波方程,采用交错网格有限差分数值求解算法,对浅层各向同性弹性介质进行了包括瑞雷面波和体波在内的全波场模拟. 提出了变系数吸收边界条件并将之应用于正演模拟,使边界条件的处理简单而高效,同时给出了角点的处理方法. 对工程勘察中常见的连续和层状介质模型进行了模拟,获得了更加接近实际情况的地震记录. 结合模拟记录,探讨了瑞雷面波的形成条件,同时讨论了震源埋深对面波能量的影响.
An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation
[J].DOI:10.1190/1.2757586 URL [本文引用: 1]
Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling
[J].DOI:10.1190/1.3463431 URL [本文引用: 1]
一阶弹性波方程交错网格高阶差分解法稳定性研究
[J].提高计算精度和运算效率是所有波场正演方法所追求的目标,本文通过将速度 (应力)对时间的奇数阶高阶寻数转化为应力(速度)对空间的导数,运用时间和空间差分精度 均可达任意阶的高阶差分法,通过交错网格技术,对一阶速度-应力弹性波方程进行了数值求 解.波场快照以及实际模型的正演结果表明,这种求解一阶弹性波方程的高阶差分解法,和 常规的差分法相比网格频散显著减小,精度明显提高,而且可以取较大的空间步长,提高计算 效率。
地震叠前逆时偏移中的去噪与存储
[J].
DOI:10.3969/j.issn.0001-5733.2010.09.017
Magsci
[本文引用: 1]

地震叠前逆时偏移是当前公认的地震成像的有效途径,然而它面临着计算量甚巨,低频成像噪音以及存储量大等问题,因此,业内科研工作者对其研究乐此不疲.借助GPU/CPU协同计算可以有效解决计算量的难点,笔者已在另文中阐述,本文着重探讨成像噪音抑制以及存储问题.文中分析了叠前逆时偏移产生成像噪音的机制,据此提出在叠前地震资料中先对数据进行相位与振幅校正,进而在成像后运用拉普拉斯算子滤波法消除成像噪音,从而有效去除成像所产生的低频噪音;针对存储量,采用随机边界,用计算换存储,并借助GPU实现,节省了GPU与CPU之间的数据通讯,数值实验结果表明,采用随机边界方法的逆时偏移结果与直接存储波场的方法得到的结果差别甚小.
Multichannel analysis of surface waves
[J].DOI:10.1190/1.1444590 URL [本文引用: 1]
The dispersion of surface waves on multilayered media
[J].