0 前言
反Q滤波方法因为其计算速度快,能够有效补偿衰减能量,提高资料的分辨率而被提出并得到了广泛应用[5,6,7]。反Q滤波方法应用最广泛的是在波场外推过程中,在每一步实现反Q滤波[8,9,10,11],除此之外还有应用傅里叶级数展开方式的反Q滤波方法[12,13,14]及其它类型的反Q滤波方法[15,16]。但是反Q滤波方法是基于一维波场反向传播的,在处理复杂地质构造时存在明显的问题,因此反Q偏移成像方法逐渐得到了发展。1994年,Dai和West[17]基于伪谱法实现了黏声波叠后深度偏移,以实现对地震波的衰减进行补偿。1995年,Mittet和Sollie[18]在频率域运用褶积滤波方法实现了黏声波叠前深度偏移。2007年,Deng Feng等[19]基于达朗贝尔黏声介质实现了三维保幅叠前深度偏移方法。2010年,Zhang[20]基于频散关系推导了一种伪微分黏声波动方程。2012年,Fletcher等[21]基于声波方程,在互相关成像之前对振幅和相位进行校正,进而实现黏声波逆时偏移成像,实现对地震波衰减补偿。在黏声波场反向外推的过程中,高频分量快速增长,导致数值计算不稳定现象发生,为了解决这个问题,添加正则化算子方法[22,23,24,25,26]、低频滤波方法[27]和伴随算子方法[28]得到提出和发展,并成为克服黏声反向传播高频不稳定的主要方法。
近些年来由于地震勘探的目标越来越复杂,勘探精度越来越高,所以地震波成像方法逐渐向小尺度构造、起伏地表、复杂介质等方向发展[29,30,31,32]。为了得到高精度的成像剖面,需要发展高精度的、能够准确模拟地下复杂介质的正演模拟算法[33,34,35,36,37,38],逆时偏移[39,40,41]成像方法能对高陡构造进行很好的成像,所以受到了广泛关注。但是传统偏移方法大多数都是采用正演算子的共轭来代替它本身的逆,这会导致一系列成像问题,如低频噪声、低信噪比、成像振幅不均衡及采集脚印等。最小二乘偏移方法是一种线性反演方法,其不仅可以提高成像剖面的分辨率,还可以压制偏移噪声得到真振幅剖面。2014年,邓文志和李振春等[42]应用规则化算子及伪谱法实现了一种新的保幅最小二乘偏移算法。2015年,刘玉金和李振春[43]基于最小二乘理论和算法提出了一种扩展成像条件下的成像方法,能够在初始速度模型存在一定误差情况下获取真振幅的LSRTM成像结果。然而,最小二乘偏移方法涉及到庞大的计算量问题,因此如何提高计算效率成为最小二乘偏移方法的研究重点和热点。2000年,Romero[44]对动态编码和静态编码策略进行了比较,动态编码方式每次迭代采用不同的编码方式,而静态编码方式在每次迭代时都使用相同的编码方式。2011年,Schuster[45]总结了信噪比与迭代次数和超道集数量的关系,并对最小二乘偏移成像和叠加成像两种方法应用了相位编码技术。2012年,Huang[46]将动态分频编码方式应用到最小二乘逆时偏移方法中。
1 三维黏声最小二乘逆时偏移基本原理
1.1 三维黏声波动方程
对于L个标准线性体的黏声介质,设速度变量为v=v(u, l, w)T,则三维黏声标量波动方程的具体表达式为:
其中,l=1,2,…,L。
为了求解的方便,将二阶导数进行降阶处理,转化为一阶函数求导,从而提高了正演模拟的精度,引入辅助微分算子
上式中:GR是弛豫模量;τσl和
式中:ω代表纵波源中心圆频率,QP代表纵波的品质因子。
1.2 三维黏声波交错网格高阶有限差分数值模拟
图1
上式中:u、l、w分别为速度场在x、y、z方向的分量,ul、ll、wl分别是中间变量,P代表应力场,R代表记忆变量。
文中采用的三维情况下的稳定性条件为
其中对于Δxi,当取1、2或3时分别对应Δx、Δy或者Δz;cu为最高的高频极限速度。
当所有方向的空间网格间距都相等时,条件(5)简化为:
1.3 三维黏声最小二乘伴随算子的构建
基于Albert Tarantola对数据空间标量乘法的定义,可以得到标量乘法:
在对地震波正演模拟计算时,首先是将波动方程进行线性化处理,在求解黏声逆时偏移伴随算子时,根据式(7)定义的方程,得到伴随算子满足的标量乘法:
式中:L是将波动方程线性化的算子,L*是L的伴随算子,同理,p*就是波动方程线性化算子L伴随算子L*下的正演数据的波场值。将最原始的方程代入到式(8)中,得到
为了求解上述方程,还需要给出相应的初始边界条件,初始边界条件的表达式为
则方程(9)被整理为
伴随波场满足的边界条件为
通过推导可得到三维黏声波伴随算子满足的波动方程(具体推导见附录A):
三维黏声波伴随算子可通过下式所示的离散格式进行求解:
1.4 黏声LSRTM实现流程
最小二乘偏移理论的实质就是在地震反问题中求解最优解的过程。在最小二乘意义下最小化模拟数据与观测数据的误差方程,然后使用扰动模型更新初始模型以获得最终的成像结果。笔者主要是在了解梯度法的基础上,利用预条件共轭梯度法求解最小二乘最优解。最小二乘逆时偏移可以使用下面的迭代公式进行计算:
式中:m是模型参数;dk(k)是经过第k次修正之后的梯度方向;β(k)是迭代求解的步长。梯度和步长由式(18)~(21)求得:
式中:g(k)和α(k)是由最速下降法求解获得的梯度方向与步长。假设步长α满足抛物线的性质,利用插值法求解。L是线性正演算子;T表示矩阵的转置;dobs是观测数据;LT是偏移算子;C表示预条件算子,通过该预条件算子可以使反演问题更稳定、收敛速度更快。在文中,我们的预条件算子是使用的震源波场照明方法。
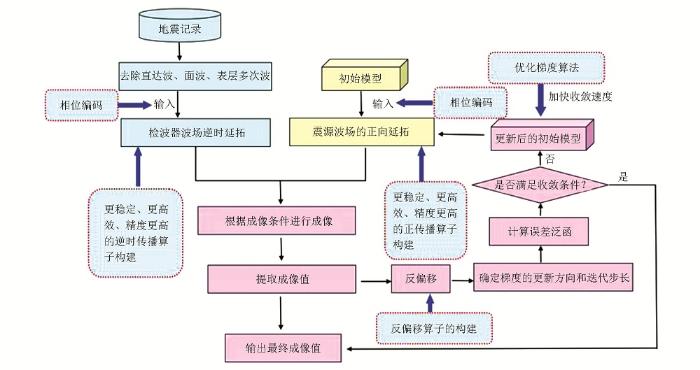
图2为黏声波最小二乘逆时偏移成像的技术路线图,图中主要分为三个部分:第一部分是黏声波正演模拟,第二部分是黏声波逆时偏移,第三部分是最小二乘逆时偏移迭代的过程。
图2
从流程图上可以看到正演部分的核心技术是构造高精度的正演算子。逆时偏移部分的关键是稳定高效的逆时传播算子的构建,最小二乘逆时偏移部分的关键就是稳定的反偏移算子的构建,解决计算量问题的关键就是引入合理极性编码技术(见附录B)。地震波在黏弹(声)介质中反向传播时,会出现高频不稳定现象,通常采用加正则化算子方法、低频滤波方法和伴随算子方法。本论文采用黏声波伴随算子的方法克服反向传播的高频不稳定,因此,对于本论文提出的三维黏声最小二乘逆时偏移来说,最关键的环节就是黏声波伴随算子的引入和计算。在迭代过程中,为了简化,假设品质因子参数和密度参数都是准确的,也就是说,品质因子和密度的扰动为零,而p参数存在扰动。
2 模型试算
2.1 Marmousi模型
与常规逆时偏移方法一样,黏声波最小二乘逆时偏移成像也需要分为三个部分:第一部分是震源波场的正向延拓,第二部分是检波场的反向延拓,第三部分是利用成像条件对其进行偏移成像。由于黏声最小二乘逆时偏移成像方法需要在避开不稳定性问题的同时对黏滞性的吸收衰减进行补偿,故其关键技术就是如何构建稳定的逆时传播算子。笔者主要运用伴随算子对其进行求解,以确保逆时传播算子的稳定性。为了验证方法的准确性,先运用二维黏声最小二乘逆时偏移方法对Marmousi模型进行方法测试,通过声波逆时偏移与黏声波逆时偏移成像效果对比,来验证黏声波方程对地震波在构造深部高波数能量的补偿作用,通过声波与黏声波最小二乘逆时偏移成像对比,来凸显在反演框架下的地震偏移成像的优势。
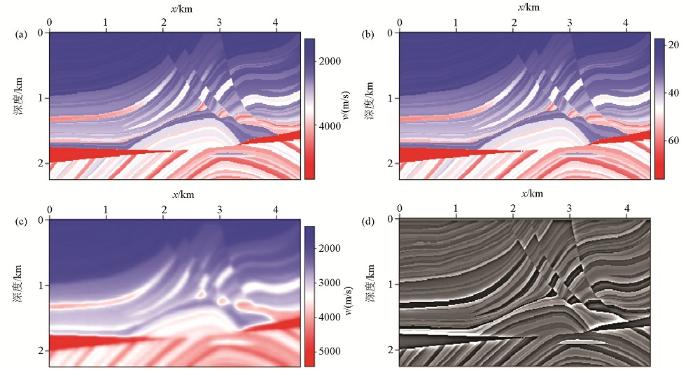
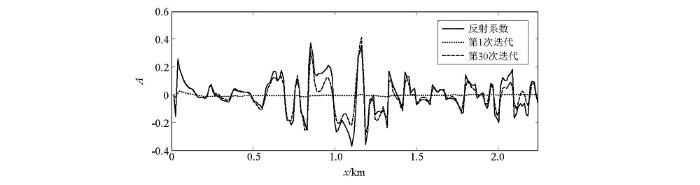
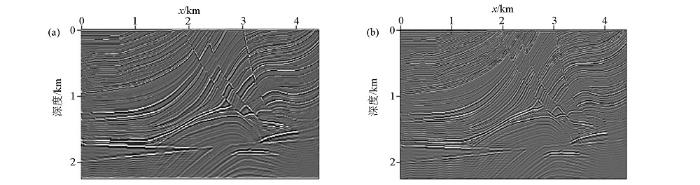
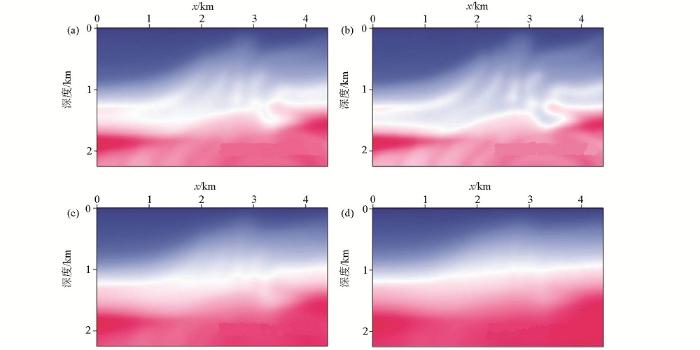
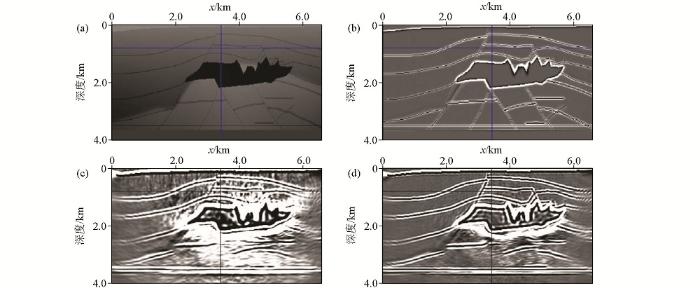
图3所用的Marmousi模型大小为4 416 m×2 244 m,横向采样点数为369,纵向采样点数为188,纵横向空间采样间隔12 m。图3a是真实的速度模型,图3b为偏移所用的Q模型,图3c为平滑P波速度模型,图3d为慢度扰动模型。均一的密度为 2.0 g/cm3。地表以下12 m处等间隔放炮148炮,检波器总数为369个,为了确保数值求解的稳定性,采样步长为0.5 ms。图4是对应的成像结果,其中图4a是声波逆时偏移的结果,图4b是黏声波逆时偏移的结果,图4c是声波最小二乘逆时偏移第30次迭代的结果,图4d是黏声波最小二乘逆时偏移第30次迭代的结果。图4a与图4b的偏移成像结果表明,在构造的浅部两种偏移方法都能对构造进行精确的成像,但是在深层,常规声波逆时偏移得到的成像结果同相轴变得模糊不清,分辨率很低,深部能量较弱,而黏声波逆时偏移由于补偿了地震波的高波数成分,所以获得了成像结果清晰、能量均衡的偏移剖面。但是黏声波逆时偏移的偏移剖面上同样存在着低频噪声、对深部储层成像分辨率不高且振幅不均衡的问题。为了解决这些问题,将逆时偏移成像结果作为最小二乘反演的第一步输入,通过求取相应的梯度和步长来不断更新成像结果,最后实现对深部构造成像的目的。图4c展示的是常规声波最小二乘逆时偏移的成像结果。与图4d对比,发现以声波LSRTM成像为理论的成像方法,不仅不能准确校正介质黏滞性引起的速度频散问题,而且还致使反射界面的空间归位不准确,反射界面空间的波场特征、振幅变化和反射系数不准确,引入成像假象。由于该方法没有对地震波的衰减进行补偿,所以其成像振幅与真实的慢度扰动相比,远小于后者。图4d是黏声波LSRTM迭代30次的偏移成像结果,当迭代30次时,成像振幅得到了补偿,能量得到了均衡,衰减了的高波数成分得到了有效恢复,压制了逆时偏移中存在的低频噪声,同时校正了由于弱照明区域照明不均衡所引起的模型横向变化问题。图5所示为x=2 760 m处反射系数与成像结果单道对比。从图中可以看出,第一次迭代的成像结果振幅能量较弱,而经过30次迭代后,成像结果的振幅能量与真实成像结果(反射系数)能量接近,而且因黏声介质造成的相位变化也得到了很好的校正。因此,文中的黏声最小二乘逆时偏移成像算法能够得到高质量的保幅成像结果。
图3
图4
图5
为了证明本文黏声伴随算子方法对低频滤波方法和添加正则化项方法的优势,给出了两种算法的对比(低频滤波方法与添加正则化项方法本质上是相同的,都是对高频成分进行滤波,只是实现方式不同,这里只给出低频滤波方法的结果),如图6所示。可以看出,采用低频滤波方法损失了部分有效能量,而本文方法振幅的保幅性更好。
图6
图7
图8
2.2 三维简单模型测试
随着地震勘探难度的增加,二维地震数据处理已经不能满足勘探需求,如今面临的勘探都是三维地震勘探,即地震数据正从二维向三维过渡,如何发展高精度的三维偏移成像方法,已迫在眉睫[47]。在二维研究的基础上,增加一维,发展到三维,实现了三维黏声最小二乘逆时偏移。
图9
图10
2.3 三维盐丘模型测试
图11
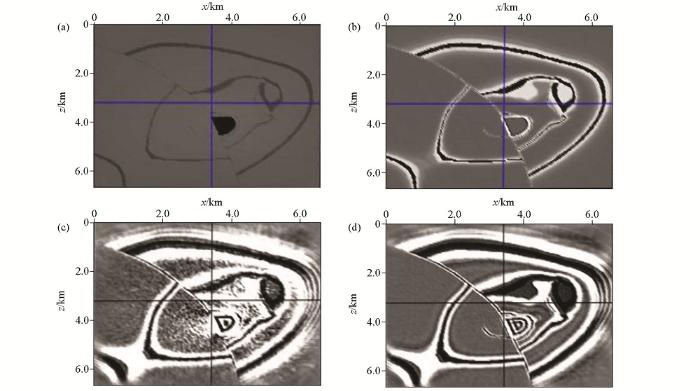
图12
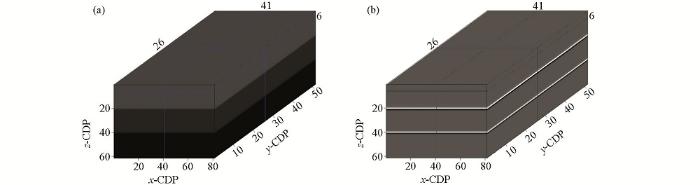
从图11c和12c偏移结果可以发现,在模型的浅部区域,第1次迭代结果就取得了分辨率较高的成像结果,但是截取部分的成像品质非常不理想,存在明显的低频噪声;当迭代到20次时,已经可以比较好地对构造进行成像,均衡了两侧的振幅,解决了弱照明区域成像质量差的问题。不仅如此,应用三维黏声最小二乘逆时偏移成像技术,还可以补偿地下介质对地震波的吸收衰减,尤其是地震波的高波数成分。
3 结论与认识
1) 常规逆时偏移方法存在固有的低频噪声,在野外实际地震资料采集的过程中,观测系统的不规则性也会对偏移成像结果产生重大影响。因此,为了获得高品质的成像结果,需要将成像引入到反演的框架下,发展黏声最小二乘逆时偏移成像方法。该方法不仅能补偿地震波衰减的能量,压制低频噪声和均衡振幅,还能获得高保真度、高信噪比和高分辨率的偏移成像剖面。
2) 基于伴随状态理论,推导了3D黏声波最小二乘逆时偏移的伴随算子以及伴随算子满足的波动方程;利用黏声最小二乘逆时偏移对Marmousi模型进行测试,验证了方法的正确性;然后,利用简单的三层平层模型和三维盐丘模型截取的一部分来测试方法的有效性,最终得到了高品质的成像效果。
3) 采用编码技术将多炮数据压缩为一个超道集,三维黏声最小二乘逆时偏移的计算量降为一个单炮的数量级,使得三维黏声最小二乘逆时偏移的实际生产应用成为可能。
4) 将三维黏声最小二乘逆时偏移应用于实际生产时,除了要考虑计算量外,还需要获得较为准确的偏移速度和品质因子。采用黏声全波形反演方法对偏移速度和品质因子进行提取是目前最热门的研究方向,子波提取的准确性也是决定该方法成像效果的决定性因素之一。
附录A 三维黏声最小二乘逆时偏移伴随算子
将伴随算子满足的边界条件代入到式(12)中,则式(12)简化为:
为了推导公式的方便,将方程中代表黏滞性的这一项用一个变量进行替代,即:
为了研究的方便,首先以x方向为例进行公式的推导,把对空间函数的求导和褶积运算做展开处理,然后变换积分顺序,得到(A3)式:
方程(A1)转化成:
将
设与黏滞性有关项的变量满足如下关系,即
故(A5)式最终化简为:
同理,y方向的表达式为:
同理,z方向的表达式为:
把式(13)、(14)、(A7)和式(A8)代入到式(11)中,经过一系列的化简,得到了初始波动方程和它的伴随算子满足的波动方程及其边界条件:
将中间变量A*(t)代入式(A10),得到伴随方程的显式表达形式:
附录B 极性编码实现步骤
极性编码技术的实现步骤,可以从以下几点出发:
1)构建超道集。对于固定的采集系统,编码的多震源数据可以写成:
其中:S是组成超道集的炮集数量;Pi是编码时使用的编码函数,当Pi是编码矩阵时,可以确保
假设每一道的正演数据di与反射率模型m之间满足
其中,Li是线性正演模型的算子。将式(B2)代入到式(B1),有:
这里将超道集的正演模型算子定义为:
2)多震源数据的偏移成像。由于式(B4)给出了超道集的正演模型算子,因此根据超道集的正演模型算子可以得到超道集的偏移算子,即
则组成超道集的偏移结果可以通过下式给出:
观察上面的偏移成像结果发现,最终的成像结果由两部分组成:第一部分是标准的偏移成像结果,第二部分是超道集之间相互混叠的时候产生的串扰噪声;串扰噪声项幅值大小会依据不同的相位编码函数而不同。
文中进行编码的函数为:
3)极性编码之后的偏移成像计算。在研究极性编码最小二乘逆时偏移方法的时候,根据第一部分定义的超道集,将超道集代入到之前定义的最小二乘梯度公式中,通过化简整理发现,随着最小二乘逆时偏移模型的不断迭代更新,串扰噪声不断地得到压制。
参考文献
Wave propagating in anisotropic linear viscoelastic media:theory and simulated wave-fields
[J].DOI:10.1111/gji.1990.101.issue-3 URL [本文引用: 1]
地震波衰减机理及能量补偿研究综述
[J].随着中、浅层油气勘探程度的不断提高,深层油气藏的勘探已经成为当今勘探研究的主要对象,而深层油气勘探要获得突破关键是用于综合研究的地震剖面要有较高的信噪比和分辨率,深层与浅层能量均衡.因此,国内外对地震波衰减机理和补偿方法进行了大量研究.本文综述了基于岩石物理和散射理论的地震波的衰减机理,重点概括了地震波衰减的影响因素,指出衰减与孔隙度、频率、温度、压力、岩性等因素有关,最后分类介绍了各种地震波衰减的能量补偿方法.
地震波衰减及补偿方法
[J].
DOI:10.11720/wtyht.2015.3.04
Magsci
[本文引用: 1]

<p>地震波在地下介质中传播时,由于地下介质的吸收衰减作用,地震波的部分弹性能量不可逆转的转化为热能而发生耗散,使得地震波的能量发生衰减,相位产生畸变,降低了地震资料的分辨率和信噪比。为了实现对地震波的吸收衰减进行补偿,国内外许多学者在这方面做了大量的研究工作。笔者简单介绍了地震波的衰减机制和影响地震波衰减的主要因素,重点概括了各种地震波衰减补偿的研究方法,如反<em>Q</em>滤波方法、时频分析方法和反<em>Q</em>偏移方法,分析了各种补偿方法的优缺点。最后用黏声波逆时偏移方法对地震波衰减进行了补偿,并预测了地震波衰减补偿研究的发展趋势。</p>
Plane-wave Q deconvolution
[J].DOI:10.1190/1.1442011 URL [本文引用: 1]
Inverse Q-filtering:a spectral balancing technique
[J].DOI:10.1111/gpr.1987.35.issue-6 URL [本文引用: 1]
Modeling of attenuation and dispersion
[J].DOI:10.1190/1.1443500 URL [本文引用: 1]
An inverse Q-filter algorithm based on stable wavefield continuation
[J].DOI:10.1007/s11770-007-0040-9 URL [本文引用: 1]
Similarity and the inverse Q filter:some simple algorithms for inverse Q filtering
[J].DOI:10.1190/1.1443307 URL [本文引用: 1]
A stable and efficient approach of inverse Q Filtering
[J].DOI:10.1190/1.1468627 URL [本文引用: 1]
Inverse Q-filter migration
[J].DOI:10.1190/gpysa7.73.1so_1 URL [本文引用: 1]
近地表Q值求取及振幅补偿
[J].利用面波衰减的Q模型,反演出近地表的Q值.据此,给出消除振幅受近地表影响的振幅静校正,利用时间剩余静校正方法解决了振幅问题.实际计算结果表明本文方法能有效地去除振幅异常.
Plane-wave Q deconvolution
[J].DOI:10.1190/1.1442011 URL [本文引用: 1]
用于深度域地震剖面衰减与频散补偿的反Q滤波方法
[J].根据地震波在非弹性介质中的传播规律,本文提出了一种在深度域地震剖面进行反Q滤波的新方法. 在深度域的Q滤波算子符合地震波在衰减介质中的传播规律,不仅考虑了介质吸收对地震波振幅的影响,而且还保证了所造成的波形畸变满足因果规律,即地震体波具有某种频散性质. 利用该方法处理了2条总长度约60km的某浅海地区叠后深度偏移地震剖面. 合成记录剖面的正演和反演计算结果表明,在对地震剖面进行深度域反Q滤波之后 ,不仅达到了压缩中、深部目的层子波宽度提高分辨率和信噪比的目的,而且保持了原始地震剖面的整体形态和能量分布.
Estimation of inverse Q filtering for prestack reflected PP and converted PS waves
[J].DOI:10.1007/s11770-009-0009-y URL [本文引用: 1]
Inverse Q Migration
[C]//
Prestack depth migration with compensation for absorption and dispersion
[J].DOI:10.1190/1.1443882 URL [本文引用: 1]
True-amplitude prestack depth migration
[J].DOI:10.1190/1.2714334 URL [本文引用: 1]
Compensating for visco-acoustic effects in reverse-time migration
[C]//
Wavepath-consistent effective Q estimation for Q compensated reserve-time migration
[C]//
The least-squares reverse time migration for viscoacoustic medium based on a stable reverse-time propagator
[C]//
The application of pseudospectral method and a stable reverse-time propagator for viscoacoustic RTM
[C]//
A new reverse time migration method for viscoacoustic VTI medium
[C]//
Viscoacoustic anisotropic full waveform inversion
[J].DOI:10.1016/j.jappgeo.2016.12.001 URL [本文引用: 1]
Attenuation compensation in anisotropic least-squares reverse time migration
[J].DOI:10.1190/geo2016-0677.1 URL [本文引用: 1]
Q-compensated reverse-time migration
[J].
Q-compensated reverse-time migration
[J].
复杂地表条件下共反射面元(CRS)叠加方法研究
[J].在地表地形复杂的情况下,静校正不易做好,这是制约山地资料处理质量的一个很重要的因素.复杂地表共反射面元(CRS)叠加不需对叠前数据做静校正,而且在得到叠加剖面后可以利用叠加得到的波场参数剖面实现基准面重建.地震数据的试算表明,复杂地表CRS叠加得出的剖面与常规处理剖面相比有着较高的信噪比和同相轴连续性.与水平地表CRS叠加不同的是,在复杂地表CRS叠加的时距公式中,波场三参数耦合,难以通过简化CRS道集的方法将它们全部分离并逐个优化.引入模拟退火算法后,有效地解决了这一组合优化的难题.
地震偏移成像技术研究现状与发展趋势
[J].地震偏移成像是在一定的数学物理模型(声介质、弹性介质等)基础上,应用相应的地球物理理论,将地面观测到的多次覆盖数据反传,消除地震波的传播效应并得到地下介质模型图像的过程。本文首先从不同的分类角度对地震偏移进行了简单评述,较为详细地阐述了如今广泛应用的几类叠前深度偏移方法,分析了计算效率和成像精度、保幅性、起伏地表以及介质复杂性对偏移成像适用性的制约,指出选取偏移成像方法时需要具体问题具体分析,要明确方法的假设条件和适用范围。最后通过总结近年来SEG/EAGE会议及出版物中有关地震偏移成像的讨论专题,展望了地震偏移未来走向和发展趋势,可以概括为:①叠前深度偏移已经成为地震偏移的研究主流;②逆时偏移逐步由理论研究步入工业化应用;③地震偏移成功地从二维走向三维;④起伏地表偏移受到广泛关注;⑤TI、VTI和TTI介质偏移成为研究热点;⑥反演偏移已经作为偏移领域的新宠登上历史舞台。
裂缝型储层时空双变正演模拟研究
[J].
DOI:10.6038/pg20140324
Magsci
[本文引用: 1]

<p>本文将深层裂缝型储层视为各向同性背景下的小尺度非均质体,采用时空双变正演模拟算法模拟其地震响应,并将Lanczos滤波算子推广到该算法中,在保证最优的计算效率及内存的前提下,解决了常规变网格算法长时间采样下的不稳定问题.测试结果验证了本文算法对深层微构造的模拟精度及效率.最后将本算法应用到裂缝储层正演模拟中,定量分析了不同裂缝开度、密度和倾角下的地震振幅响应规律,为裂缝型储层的检测和解释提供了可靠的理论指导.</p>
高精度双吸收边界条件在地震波场模拟中的应用(英文)
[J].DOI:10.1007/s11770-014-0463-z URL [本文引用: 1]
波动方程时空域有限差分数值解及吸收边界条件研究进展
[J].波动方程数值解是波动方程正演、逆时偏移和全波形反演的核心技术之一。本文对波动方程数值求解的有限差分技术和吸收边界条件进行了分析,重点总结了基于时空域频散关系的有限差分、自适应可变空间算子长度有限差分、优化有限差分及混合吸收边界条件等方法,介绍了这些方法在逆时偏移和波形反演中的应用。
任意偶数阶精度有限差分法数值模拟
[J].本文从Taylor级数展开式出发,推导出了任意阶导数的任意偶数阶精度差分格式。文中给出了计算相应差分系数的公式,并计算出了一阶、二阶、三阶和四阶导数的若干阶精度差分系数。最后讨论了声波方程的任意偶数阶差分数值解的稳定性条件,并进行了数值模拟试验。结果表明差分精度越高,频散越小,数值模拟的效果越好。
基于优化时空域高阶有限差分方法的粘滞声波叠前逆时偏移(英文)
[J].DOI:10.1007/s11770-014-0414-8 URL [本文引用: 1]
基于稳定逆时传播算子的黏声介质最小二乘逆时偏移
[J].
DOI:10.11720/wtyht.2015.4.22
Magsci
[本文引用: 1]

<p>基于GSLS模型黏声介质二阶拟微分方程,采用伪谱法进行数值模拟。针对黏声介质逆时传播过程中产生的高频不稳定问题,提出加入规则化算子对其进行消除的方法,构建了稳定的逆时传播算子。在最小二乘反演的基础上,将黏声介质逆时偏移与最小二乘思路相结合,发展了带有振幅补偿的黏声介质最小二乘逆时偏移(LSRTM)。Marmousi模型结果表明:相对于常规最小二乘逆时偏移,黏声介质最小二乘逆时偏移校正了地层的黏滞性,得到了更加精确可靠的保幅成像剖面。</p>
Phase encoding of shot records in prestack migration
[J].
Theory of multisource crosstalk reduction by phase-encoded statics
[J].DOI:10.1111/gji.2011.184.issue-3 URL [本文引用: 1]
Multisource least-squares migration of marine streamer and land data with frequency-division encoding
[J].DOI:10.1111/gpr.2012.60.issue-4 URL [本文引用: 1]