系统聚类法在划分岩溶地下水化学类型中的应用

doi:10.11720/wtyht.2018.1566

系统聚类法在划分岩溶地下水化学类型中的应用

杨艳林¹, 邵长生¹, 靖晶²

1. 武汉地质调查中心,湖北武汉 430205

2. 中国地质大学(武汉) 环境学院,湖北武汉 430074

The application of systematic clustering method to the classification of chemical types of karst groundwater

YANG Yan-Lin¹, SHAO Chang-Sheng¹, JING Jing²

1. Wuhan Center, China Geological Survey, Wuhan 430205, China

2. School of Environmental Studies, China University of Geosciences, Wuhan 430074, China

责任编辑: 蒋实

收稿日期: 2017-12-15 修回日期: 2018-03-24 网络出版日期: 2018-08-05

基金资助:

中国地质调查局“长江中游城市群咸宁—岳阳和南昌—怀化段高铁沿线1:5万环境地质调查”项目. DD20160248

Received: 2017-12-15 Revised: 2018-03-24 Online: 2018-08-05

Fund supported:

. DD20160248

作者简介 About authors

杨艳林(1984-),男,博士,主要从事水工环地质调查工作。Email:yangyanlinjida@gmail.com 。

摘要

基于前人的研究及咸宁岩溶地区地下水化学类型判别,知舒卡列夫分类法存在一些不足,提出了系统聚类分析法。文中对系统聚类法的4个过程(矩阵构造、相似程度表征、消除量纲差异和样本系统聚类)进行了详细讨论,编制了相应的程序,并将其应用于咸宁岩溶地区采集的水样,取阈值3.2时可分为10类,最后对每种水化学类型与舒卡列夫分类进行了对比分析,效果较好。

关键词： 系统聚类分析 ; 岩溶地区 ; 地下水 ; 化学类型

Abstract

The previous methods for the discrimination of groundwater hydrochemical types in karst areas of Xianning, such as the ShuKaliefu's classification, have some shortcomings. In view of such a situation, this paper proposes the systematic cluster analysis method. The four processes of the system clustering method, i.e., matrix construction, similarity degree representation, elimination of dimensional difference and sample system clustering, were discussed in this paper. The corresponding programs were compiled for the systematic cluster method, and the groundwater from the karst area of Xianning was taken as an example. When the threshold is 3.2, the hydrochemical type can be divided into 10 categories. Finally, a comparative analysis of each classification was carried out with Shug Kalev classification, and it is proved that the systematic cluster analysis method is effective.

Keywords： systematic cluster analysis ; karst area ; groundwater ; hydrochemical type

PDF (9390KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨艳林, 邵长生, 靖晶. 系统聚类法在划分岩溶地下水化学类型中的应用. 物探与化探[J], 2018, 42(4): 738-744 doi:10.11720/wtyht.2018.1566

YANG Yan-Lin, SHAO Chang-Sheng, JING Jing. The application of systematic clustering method to the classification of chemical types of karst groundwater. Geophysical and Geochemical Exploration[J], 2018, 42(4): 738-744 doi:10.11720/wtyht.2018.1566

0 引言

地下水水化学特征及形成作用是水文地质学研究的重要内容,而地下水化学类型是描述地下水化学特征的一个综合指标,其时空变异是区域地下水水质变化的重要依据^[1,2,3]。地下水化学类型的分类方法很多,目前,在地下水化学分类中,常用的有苏林分类法、阿廖金分类法和舒卡列夫分类法,其中以舒卡列夫分类法的应用最广。目前,舒卡列夫分类法在盆地或平原等大尺度方面的研究较多,并且能较好地反映出地下水化学成分的成因或运移规律,然而在小流域尺度方面研究较少,并存在不足。如周金龙等^[4]指出在较单一的水文地质单元地区采用舒卡列夫分类法,常造成同一水化学类型水质差异较大,而不同水化学类型间水质差异不大的反常现象。周迅等^[5]指出晋江市地下水与经典舒卡列夫分类法规律并不一致。

基于舒卡列夫分类法存在的不足,一些学者提出运用数理统计的方法。如李磊等^[6]运用判别分析法成功的对盐湖水化学类型进行了判别;刘志峰等^[7]利用模糊聚类分析法对西龙河口峄山断层带水源地岩溶水化学进行分类;曹红翠等^[8]应用主成分分析和判别分析,研究了青海盐湖水化学类型,并建立了水化学类型的数学模型。基于前人的研究,以及咸宁市汀泗桥镇和赤壁市官塘驿镇区内岩溶地下水的特点,笔者提出运用系统聚类的方法对岩溶地下水化学类型进行分类,该方法不仅可以分类,而且可以用图件的形式进行说明。目前此方法在地下水化学类型识别方面应用较少,而在其他方面已经得到广泛应用。如高波等^[9]提出通过系统聚类对汛期的分期进行分析计算;马成有等^[10]将系统聚类法用于模拟地质样品中各形态铅;吴顺川等^[11]得出系统聚类法能够准确给出岩体节理分类;奥布力·塔力普等^[12]应用系统聚类法对西部地区12省区环境污染程度进行了评价,效果较好。

1 研究区概况

1.1 地质概况

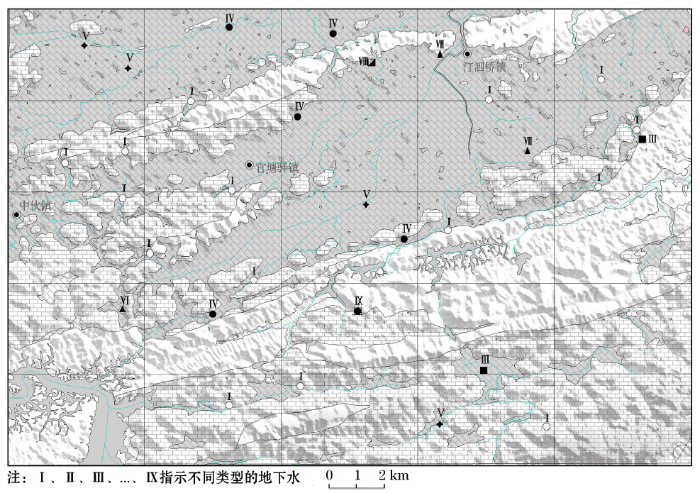
研究区的行政区包括咸宁市汀泗桥镇和赤壁市官塘驿镇,属于亚热带季风气候区,位于幕阜山脉北缘地带江汉平原南缘相接,总体地势为南东高、北西低;所处的大地构造位置是扬子准台坪和幕阜台坳过渡地带,其区域构造格局恰好处于近EW向咸宁台褶束,与NNE向郯庐断裂系相交地带。区内为沉积岩覆盖,出露地层简单,主要有新生界第四系全新统和更新统,中生界三叠系中统嘉陵江组和下统大冶组,古生界二叠系上统大隆组、龙潭组,中统茅口组、栖霞组和下统的梁山组,石炭系上统黄龙组、大浦组以及志留系上统茅山组、中统坟头组地层^[13,14,15]。

1.2 岩溶区水文地质条件

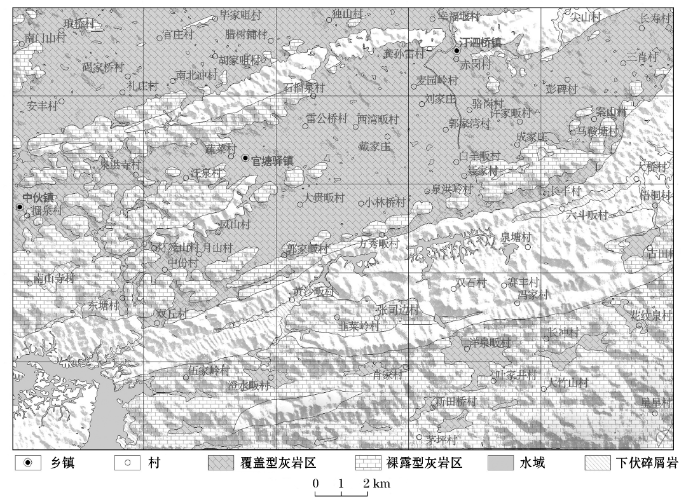
根据含水介质特征,将工作区内的地下水类型分为松散岩孔隙水、碎屑岩基岩裂隙水和碳酸盐岩溶水3大类;根据地下水赋存条件进一步将碳酸盐岩溶水分为裸露型和覆盖型两个亚类。松散岩孔隙水分布于平原区浅部,以及丘陵山区的岩溶洼地、谷地。碎屑岩裂隙含水岩组为志留系上统茅山组、中统坟头组和下统新滩组,主要分布于图幅南部低山丘陵区,呈东西条带状分布。碳酸盐岩含水岩组为三叠系嘉陵江组和大治组,二叠系大隆组、龙潭组、茅口组、栖霞组和梁山组,石炭系黄龙组和大浦组,主要分布于图幅的东南角(图1)^[16,17,18]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 咸宁岩溶地区含水岩组分布

2 样品采集及测试

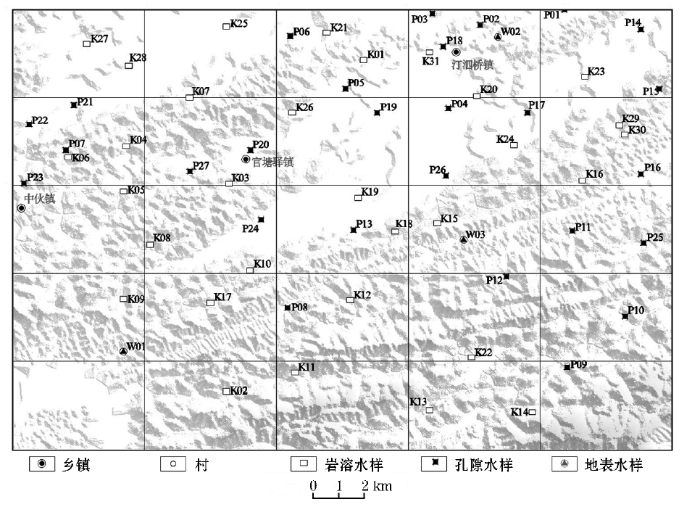
按照中国地质调查局《地下水污染地质调查评价规范(DD2008-01)》的要求,对研究区具有代表性的地下水点进行取样,共采集地下水样61组,位置分布如图2。测试指标包括pH、K⁺、Na⁺、Ca²⁺、Mg²⁺、HC $O_{3}^{-}$ 、S $O_{4}^{2 -}$ 、Cl^-、矿化度等,交由具有地质实验测试甲级、国家级计量认证的湖南省地质测试研究院进行分析测试,检测依据《生活饮用水标准检验方法无机非金属指标(GB/T 5750.5-2006)》、《生活饮用水标准检验方法金属指标(GB/T5750.6-2006)》和《地下水质检验方法(DZ/T0064-1993)》等标准,测试结果如表1。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 咸宁岩溶地区地下水采样点分布

表1 咸宁岩溶地区地下水采样点测试数据mg/L

离子	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11	P12	P13
HC $O_{3}^{-}$	77.9	86.3	59.8	76.0	79.7	68.6	88.6	73.4	91.6	94.6	86.7	69.3	80.6
Cl^-	5.7	3.8	14.9	13.1	8.7	10.4	1.2	5.9	1.4	0.6	3.7	11.9	3.7
S $O_{4}^{2 -}$	16.4	9.9	25.3	10.9	11.5	21.0	10.2	20.6	7.1	4.8	9.6	18.8	15.7
Na⁺+K⁺	9.6	10.2	25.5	17.8	10.7	8.0	2.3	14.5	7.6	1.6	8.3	16.7	8.5
Ca²⁺	73.3	73.1	62.1	73.9	79.9	75.6	88.0	74.9	78.4	70.5	78.8	66.4	79.1
Mg²⁺	17.2	16.7	12.4	8.3	9.5	16.5	9.7	10.6	14.0	27.9	12.9	17.0	12.4
离子	P14	P15	P16	P17	P18	P19	P20	P21	P22	P23	P24	P25	P26
HC $O_{3}^{-}$	76.5	75.6	88.4	68.5	77.2	84.8	72.0	69.1	84.6	90.5	23.7	77.1	75.3
Cl^-	4.8	8.2	2.9	17.2	4.9	3.5	19.4	16.8	4.6	1.3	71.0	8.4	10.6
S $O_{4}^{2 -}$	18.7	16.3	8.7	14.3	17.9	11.8	8.7	14.2	10.8	8.2	5.3	14.5	14.1
Na⁺+K⁺	9.7	6.7	4.0	19.1	10.0	13.1	19.7	14.7	6.1	3.6	60.5	4.7	5.8
Ca²⁺	78.9	81.5	85.6	65.8	77.8	73.8	73.6	70.1	84.9	92.9	34.9	87.6	84.9
Mg²⁺	11.4	11.8	10.4	15.1	12.2	13.1	6.7	15.2	9.1	3.4	4.6	7.7	9.3
离子	P27	K01	K02	K03	K04	K05	K06	K07	K08	K09	K10	K11	K12
HC $O_{3}^{-}$	62.9	68.3	93.8	84.1	93.5	95.1	89.5	94.4	93.8	74.5	92.3	93.2	97.6
Cl^-	21.6	23.3	0.8	0.7	0.9	0.6	0.8	1.1	0.5	6.6	0.7	0.7	0.5
S $O_{4}^{2 -}$	15.6	8.5	5.4	15.2	5.6	4.3	9.6	4.6	5.7	18.9	7.0	6.1	1.9
Na⁺+K⁺	11.9	23.9	1.5	1.7	1.5	1.1	1.1	1.9	1.5	15.8	2.0	2.1	2.2
Ca²⁺	77.3	55.6	91.8	93.4	93.4	95.7	93.5	89.9	95.5	75.2	93.3	91.1	59.1
Mg²⁺	10.8	20.6	6.7	4.9	5.2	3.2	5.4	8.2	3.1	9.0	4.6	6.8	38.7
离子	K13	K14	K15	K16	K17	K18	K19	K20	K21	K22	K23	K24	K25
HC $O_{3}^{-}$	95.6	96.7	95.5	92.1	80.4	82.5	87.5	89.8	83.5	88.2	91.5	67.4	81.8
Cl^-	0.5	0.3	0.1	1.7	4.0	4.1	2.3	3.2	6.8	4.8	5.3	2.2	5.3
S $O_{4}^{2 -}$	3.9	3.0	4.4	6.2	15.6	13.4	10.2	7.0	9.8	7.1	3.1	30.4	12.9
Na⁺+K⁺	1.0	1.4	1.9	2.6	8.8	10.1	3.2	3.8	9.7	4.8	3.3	7.6	7.3
Ca²⁺	79.4	95.0	94.5	89.8	79.5	81.6	82.0	90.8	80.9	86.7	89.6	70.3	79.6
Mg²⁺	19.6	3.6	3.7	7.6	11.7	8.3	14.8	5.4	9.4	8.5	7.1	22.2	13.1
离子	K26	K27	K28	K29	K30	K31	W01	W02	W03
HC $O_{3}^{-}$	75.7	90.0	93.6	94.2	85.2	60.3	62.0	84.0	83.2
Cl^-	14.8	5.7	2.3	1.7	9.9	7.6	3.8	3.0	1.0
S $O_{4}^{2 -}$	9.5	4.4	4.1	4.1	4.9	32.1	34.2	13.1	15.8
Na⁺+K⁺	13.5	6.5	3.1	2.4	10.3	32.2	8.5	10.8	4.0
Ca²⁺	80.2	82.4	82.4	94.8	86.0	65.0	76.5	68.1	83.1
Mg²⁺	6.3	11.1	14.5	2.8	3.8	2.9	15.0	21.1	12.9

新窗口打开| 下载CSV

3 系统聚类法

系统聚类法包括4个过程:矩阵构造、相似程度表征、消除量纲差异、样本系统聚类。

3.1 矩阵构造

设有n个采样点,进行了m个指标测试,这样n个样本的m个指标可写成矩阵形式,如式(1)。其中每一行代表一个样本,每一列代表一个测试指标。

(1)

T = (T_{ij})_{N \times m} = |\begin{array}{l} T_{11} & T_{12} & \dots & T_{1 m} \\ T_{21} & T_{22} & \dots & T_{2 m} \\ ︙ & ︙ & ︙ & ︙ \\ T_{n 1} & T_{n 2} & \dots & T_{1 m} \end{array}| 。

3.2 相似程度表征

测试样本之间的相似程度,常用样品间距离来描述,两个样品之间的距离越小,表示两者之间共同点越多;距离越大,共同点越少。目前,样品间距离有绝对值距离、平方欧氏距离、闵可夫斯基距离、切比雪夫距离和马哈拉诺比斯距离^[19]等。文中系统聚类分析距离采用的是平方欧式距离,即两样本之间的所有指标之差的平方和:

(2)

d_{ik} = \sqrt[]{\frac{1}{m} \overset{m}{\sum_{j = 1, i \neq k}} (T_{ij} - T_{kj})^{2}} 。

式中:T_ij为第i个样本中第j个指标的测量值;T_kj为第k个样本中第j个指标的测量值;d_ik越小反映两样本之间的相似程度越大,越有可能聚合成簇,由此可判断样本之间的相似程度。

3.3 消除量纲差异

由于数据在测定过程中,采用的计量单位或测试手段不同,原始数据在量值上存在较大差异。为了避免因量纲不同对聚类结果产生误差,聚类前必须对数据进行标准化,常用的方法有标准化法、正规化法、极差标准化法、极大值正规化法和均值正规化法等^[19,20]。笔者采用标准化法,使得标准化后的数据处于[0,1]之间,如第i个样本上第j个变量T_ij的变换公式为

(3)

T_{ij}^{'} = \frac{T_{ij} - {\overset{̅}{T}}_{j}}{δ_{j}} \sqrt[]{\overset{m}{\sum_{j = 1, i \neq k}} (- T_{kj})^{2}},

(4)

{\overset{̅}{T}}_{j} = \frac{1}{n} \overset{n}{\sum_{i = 1}} T_{ij},

(5)

δ_{j} = \sqrt[]{\frac{1}{n} \overset{n}{\sum_{i = 1}} (T_{ij} - {\overset{̅}{T}}_{j})^{2}} 。

其中: ${\overset{̅}{T}}_{j}$ 为变量j的均值,δ_j为变量j的标准差, $T_{ij}^{'}$ 为第i样本j变量规一化后的值。

3.4 样本系统聚类

系统聚类的基本思想是:先将待聚类的n个样本各自看成一类,共有n类;然后按照事先选定的方法计算每两类之间的距离,将距离最小的两个样本聚合为一类,其他样品仍各自为一类;如此进行下去,每次重复都减少一类,直到最后所有样本都归为一类为止。

4 程序编制

基于系统聚类的思想,在Windows平台下利用VC++开发工具,完成了地下水化学类型系统聚类算法,并进行了测试与验证。

5 结果对比分析

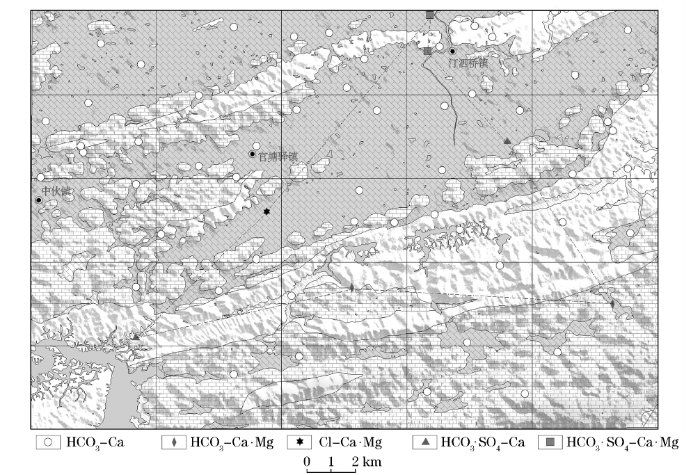
图3是按照舒卡列夫分类法划分的结果。由图可知,区内水样主要有5种类型,其中HCO₃-Ca型水样有54个,占绝大部分;HCO₃-Ca·Mg型、Cl-Ca·Mg型、HCO₃·SO₄-Ca型和HCO₃·SO₄-Ca·Na型水样分别有2个(P10,K12)、1个(P24)、2个(K24,W01)和2个(P03,K31)。由此可知,HCO₃-Ca型水样为区内的主要化学类型,但这种结果不利于从化学类型方面来分析地下水的演化模式,是地球化学分析中不想得到的结果。图4是利用系统聚类法获得的谱系图,它将HCO₃-Ca型水进一步分为多个亚类,以利于对地下水来源与去向进行深入分析。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 咸宁岩溶地区地下水采样点水化学类型舒卡列夫分类

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 咸宁岩溶地区地下水采样点谱系

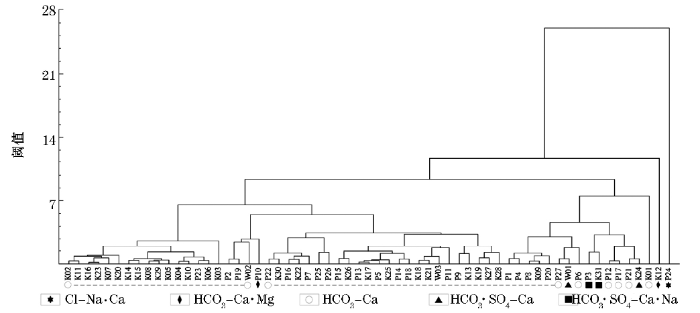
利用不同的阈值进行聚类,可以得到不同的聚类结果,结合研究区的水文地质条件,取阈值3.2,则研究区地下水可分为10类,即{K02,K11,…,K03}、{P2,P19,W02,P10}、{P22,K30,P16,…,P26}、{P15,K26,……,P11}、{P9,K13,…,K28}、{P1,P4,…,P6}、{P3,K31,…,K24}、{K01}、{K12}、{P24}。由于篇幅限制,下面仅就岩溶水样进行对比分析。图5是聚类分析后的结果图。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 咸宁岩溶地区系统聚类法岩溶地下水分类

Ⅰ类水样有15处,其中泉点10处(K02,K11,K16,K07,K14,K15,K08,K05,K04,K03)、溶潭2处(K10,K06)、水文孔2处(K23,K29)和工程孔1处(K14),分布于裸露型岩溶区或第四系覆盖较薄的地区,岩溶裂隙发育,地下水径流速度快。HC $O_{3}^{-}$ 和Ca²⁺含量在阴阳离子中所占的比例大,与舒卡列夫法相一致,为HCO₃-Ca型水。

Ⅱ类水样无。

Ⅲ类水样两处(K22和K31),均为水文孔。K22位于岩溶洼地,接受裸露型岩溶的侧向径流补给,据钻孔岩芯资料,灰岩之上覆盖有黏土、淤泥质黏土、粉砂质黏土等,达47.5 m,是较好的隔水层,与深层岩溶水无水力联系;由水文试验可知,岩溶地下水径流速度慢,且稳定水位埋深较深(42 m)。K31位于倒转向斜处,向斜两翼为志留系粉砂质页岩,隔水性好,地下水径流速度慢。两处岩溶地下水受构造控制,而舒卡列夫分类将其划为不同的水类型。

Ⅳ类水样有5处(K25,K17,K21,K26,K18),其中K25、K26为水文孔,K21为工程孔,分布于山麓平原,为地下水的变动带,丰水季时水量丰富,枯季时水量小,且溶洞较发育,如K25、K26和K21。舒卡列夫分类法也将这5处水样规为一类。

Ⅴ类水样有4处(K27,K28,K19,K13),其中K27、K28、K19均为水文孔,K13为岩溶泉,分布于向斜的近核部,为岩溶地下水的排泄区,水文孔及岩溶泉揭露(出露)的岩性均为三叠系白云质灰岩,白云质灰岩的溶解致地下水中Mg²⁺含量高。舒卡夫分类法将这4处水样规为一类。

Ⅵ类水样有1处(K09),样品中S $O_{4}^{2 -}$ 和Na⁺+K⁺离子含量较高,不同于其他水样,但舒卡列夫分类未将其区分开。

Ⅶ类水样有2处(K24和K31),均为水文孔,样点周围为岗地,水样中S $O_{4}^{2 -}$ 含量较高。据钻孔岩芯显示,灰岩上覆10 m多的黏土,入渗补给岩溶地下水有限;据抽水试验可知,两孔的单孔涌水量小,径流条件差。

Ⅷ类水样1处(K01),其Cl^-含量高,单成一类,与舒卡列夫分类相一致。

Ⅸ类水样有1处(K12),其Ca²⁺、Mg²⁺含量较高,与舒卡列夫分类相一致。

6 结语

舒卡列夫地下水化学类型分类方法将咸宁岩溶地区的地下水划分为大片区的HCO₃-Ca型水,不利于分析地下水的形成与演化过程。笔者提出运用系统聚类法进行地下水化学类型识别,并对其原理进行了详细介绍,编制了相应的程序,应用效果较好。同时,由于系统聚类法的灵活性,不局限于常规的8大离子,可根据实际需要添加一些其他指标(如TDS),有利于对地下水化学类型区划进行更深入的研究和探索,而这是舒卡列夫分类法无法做到的。笔者旨在抛砖引玉,望对岩溶地下水分析提供辅助手段。

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

沈照理

. 水文地球化学基础[M]. 北京: 地质出版社, 1986.