0 引言
经验模式分解(empirical mode decomposition,EMD)方法由Huang等[9]于1998年提出,被用来处理分析非线性、非平稳信号。它的主要原理概括为,将“复杂”信号分解成若干个从高频到低频排列的固有模态函数(lntrinsic mode function,IMF)和一个剩余分量,从而实现信号不同尺度的分解。已有应用表明该方法不仅具有多分辨率特性、自适应性,且无需任何的先验参数。自方法提出以来,已被广泛应用于计算机图像分析、数据去噪、边缘检测等众多领域[10,11,12,13,14]。 近年来,EMD方法也被应用到地球物理数据的处理中,取得了较好的应用效果[15,16,17,18,19,20]。本研究尝试将二维经验模式分解应用于重力资料的多尺度分析。
1 方法原理
EMD方法的本质是依据不同的时间尺度特征将原始信号分解为一系列不同尺度的本征模态函数信号,该方法假设任何复杂的信号均由简单的固有模态函数组成,而对于模态函数的形式无特殊要求,即每个模态可以是线性平稳的,也可以是非线性非平稳的。方法的核心原理与小波分解类似,但是小波变换需要人为划定特征时间尺度,而EMD方法则能够自适应地依据信号本身的特性设定特征时间尺度。
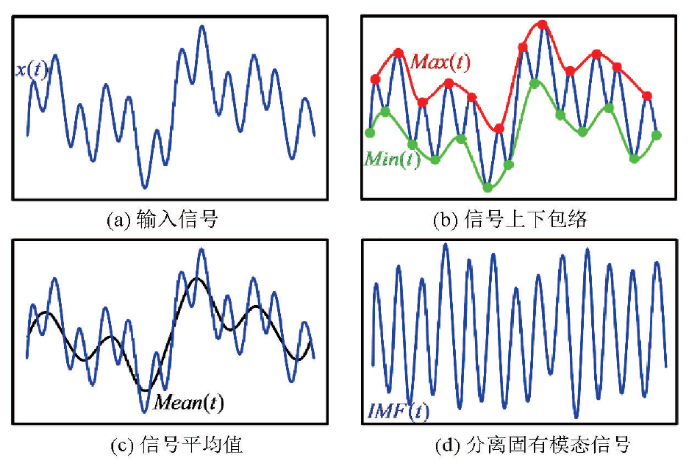
基于EMD算法的多尺度分离计算步骤如下:假设存在一维信号x(t),利用极值搜索算法找出其极大值、极小值;基于搜索出的极值点,利用插值算法求取原始信号的上下包络线Max(t)及Min(t);计算Max(t)与Min(t)的均值信号Mean(t);从原始信号x(t)中减去均值信号Mean(t)得到新的信号x'(t);根据迭代终止条件进行判断,若满足则x'(t)作为第一层级的IMF,此后将x(t)与x'(t)的差值函数作为新的输入信号进行迭代过程,得到一系列的IMF。常见的迭代终止条件有两种,一种是使得分解过程中两个相邻分解结果的标准方差值小于设定阈值作为判断某阶分解结束的条件[21];另外一个终止条件是使得x'(t)满足在整个数据空间极大值与极小值和过零点的数目之多相差一个,同时信号x'(t)的均值为零。上述的分解过程见示意图1,最终的信号可表示为:
图1
对于二维数据,上述分解过程类似,需要做的是将一维EMD方法中对于“线”的筛分拓展为对于“面”的筛分,最终得到若干二维固有模态函数和一个剩余分量,二维信号S(x,y)可最终表示为:
其中:IMFi(x,y)表示第i个二维固有模态函数,相应代表了重力数据中相对高频的成分,Res(x,y)为多尺度分离之后的剩余场,代表了重力数据中相对低频的成分。
2 模型试验
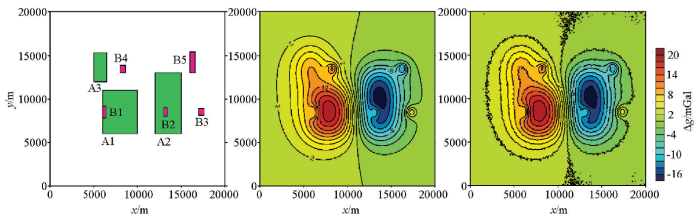
图2
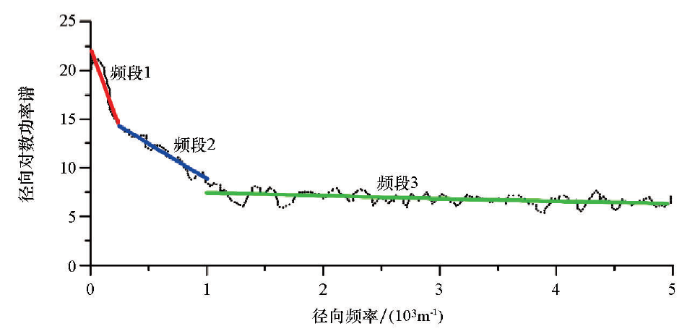
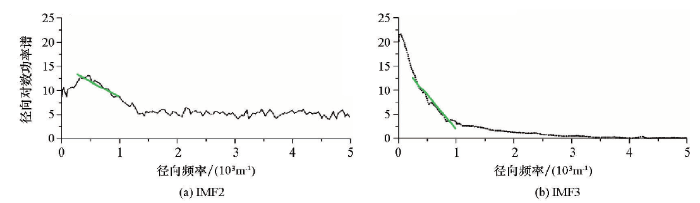
对上述加噪重力异常计算径向对数功率谱(图3),通过分析对数功率谱的形状看出该数据的频率成分主要可以分为3个频段,图中彩色线段分别为3个频段的功率谱拟合。可以大致概括为:频段1的对数功率谱主要对应于模型中A层长方体的低频异常信息,频段2的对数功率谱主要对应于模型中B层长方体的中高频频异常信息,而频段3的对数功率谱主要对应于模型中所添加随机噪声所产生的高频干扰。则在计算经验模式分解的时候,上述数据可合理地计算为3级异常数据。
图3
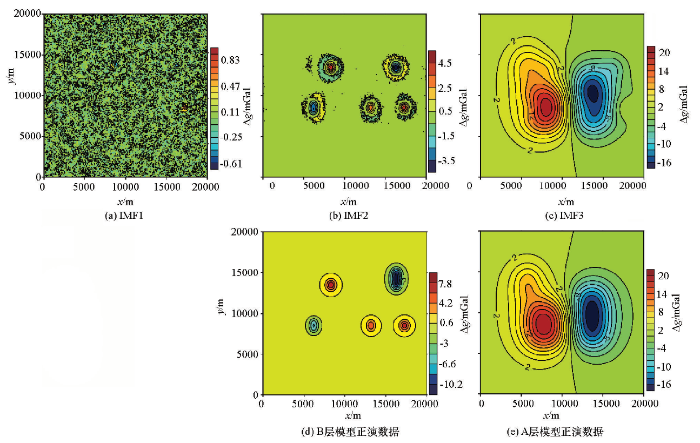
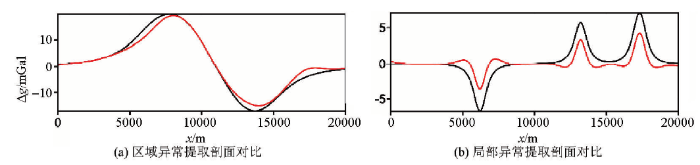
基于上述分析对加噪数据进行EMD多尺度分离计算,分离产生2级IMF和1个剩余场,见图4。第1级IMF对应于频段3的高频信息,主要为数据中的噪声,第1级IMF的剥离产生了类似于去噪的效果;第2级IMF对应于频段2的中频信息,主要为数据中B层长方体的产生异常;剩余场为数据中A层长方体产生的区域异常。为了验证此次多尺度分离的效果我们将不同层级的IMF与理论模型的正演效果进行了对比,看出分离出的局部场数据基本能够反映出浅部场源真实存在的位置及规模,分离出的区域场也很好地体现了深部场源所产生的趋势性异常。在数值上,分离后局部异常数据有些变小,主要由于还存在部分的局部场数据残留在趋势性的异常中,在趋势场异常中体现为数值的变大。这一点在图5所示的y=8 500 m处截取的剖面对比图中也可以明显看出。总体来说,基于EMD算法的重力数据多尺度分离效果较好。
图4
图5
图6
综合上述的模型试验,可以利用二维EMD方法对重力数据进行多尺度分解,得到不同层级的异常数据。分解得到的各级模式函数的异常波长与其反映的场源深度随着分解阶次的增加而增大。再结合功率谱分析方法则可以估算出不同尺度数据的场源大致深度,这有利于后续的精细处理反演和地质解释。
3 实际数据处理
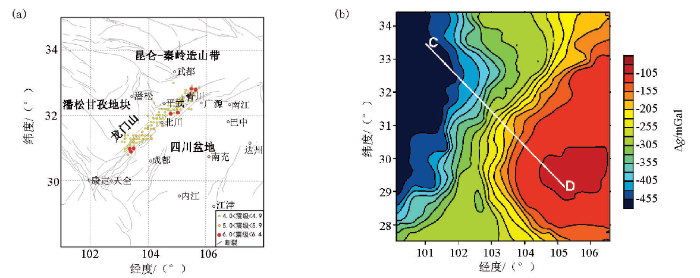
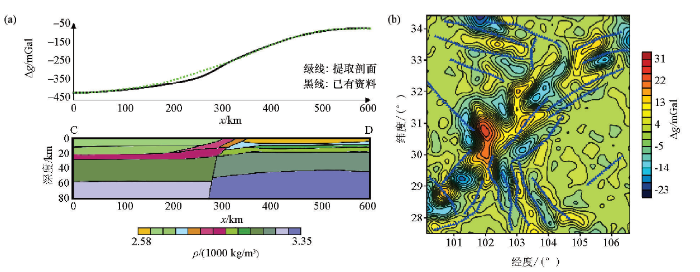
图7
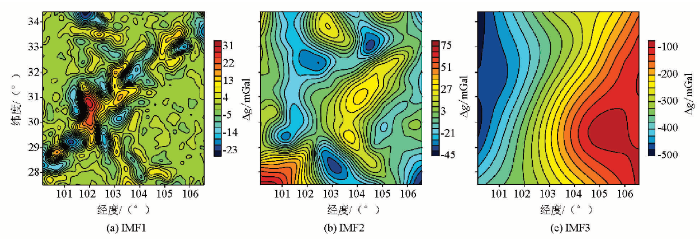
基于上文理论模型试验结果,笔者将采用EMD算法对龙门山地区重力异常进行分离试验,并与已有结果及地质信息进行对比分析。图8所示为分离之后的前3级异常数据,从分离结果看出IMF1对应了原始数据中的高频的局部重力异常,异常呈离散分布,范围相对较小,可能反映了该地区浅部岩体、构造等物性的横向变化。IMF2对应于原始数据重力的中低频信息,可能对应于相对较深的地层分布的影响,而IMF3则对应于更加低频的分量,为该区区域重力异常,可能反映了该地区深部地层、基底界面等的起伏变化。
图8
图9
同时,针对不同尺度的数据进行了场源深度的近似估计,计算得到IMF1-3所对应的深度大致为4.6 km,21.4 km和43.7 km。不同类型数据所对应场源大致深度的近似给出为后续的处理提供了有力帮助,也能够给出不同尺度重力数据的地质意义。
4 结论
笔者研究利用二维经验模式算法结合径向对数功率谱分析法对重力数据进行了多尺度分析。首先用二维经验模式对重力数据进行不同尺度的分解,分解得到的不同层级的固态模式函数对应了不同频段的重力场信息,可分别对应于高频浅层异常和中低频深部异常。利用径向对数功率谱分析方法估计各级模态函数所反映的地下场源的近似深度,定性地解释了不同深度下的场源产生的异常,较好地揭示了场源赋存的地质信息。建立了理论加噪密度模型进行了算法的测试,分离效果良好。同时将方法技术应用于实际重力资料的处理,分离结果与已有资料对应良好。
参考文献
优化滤波方法及其在中国大陆布格重力异常数据处理中的应用
[J].
DOI:10.6038/j.issn.0001-5733.2012.12.020
Magsci
[本文引用: 1]

<p>在优选延拓法的理论基础上,研究提出基于格林等效层概念和维纳滤波器的优化滤波法,用于对重力异常数据进行去噪和分离.与传统向上延拓法和优选延拓法相比,优化滤波法分离异常与延拓高度无关,不需要已知延拓高度,具有一定的优势.理论重力模型数据的去噪和异常分离试验表明优化滤波法有效,异常分离效果优于传统向上延拓法和带通滤波法.利用优化滤波法对中国大陆重力异常数据去噪和异常分离,得到有效的布格重力异常和区域重力异常.以中国大陆深地震探测推断的莫霍面深度信息为约束,对区域重力异常数据进行密度界面约束反演,得到中国大陆莫霍面深度分布.本文方法为中国大陆深部探测和区域构造研究提供一定的技术支撑.</p>
A correlation-based approach for determining the threshold value of singular value decomposition filtering for potential field data denoising
[J].DOI:10.1088/1742-2132/11/5/055007 URL [本文引用: 1]
Improved curvature gravity gradient tensor with principal component analysis and its application in edge detection of gravity data
[J].DOI:10.1016/j.jappgeo.2015.04.013 URL [本文引用: 1]
Statistical models for interpreting aeromagnetic data
[J].DOI:10.1190/1.1440092 URL [本文引用: 1]
Use of non-linear filtering for the regional-residual separation of potential field data
[J].
DOI:10.1016/j.jappgeo.2011.02.002
URL
[本文引用: 1]

Regional–residual separation is essential in gravity and magnetic data interpretation and a variety of techniques have been proposed. Graphical determination of the regional allows geological information to be taken into account. Upward continuation can be used to obtain the regional field either empirically or using some hypothesis about the geology. In some cases, a matched filter can be designed and used to separate deep and shallow sources. Simple low pass filtering has also been used but without much success. Here we propose to use a non-linear filter approach to remove gravity and magnetic anomalies smaller than a given width. This technique attempts to mimic the graphical separation method. The results from synthetic models are presented as well as the results from a case study in eastern Canada and compared to regional gravity and magnetic anomalies obtained by other techniques. Contrary to the regional fields obtained by upward continuation, non-linear filtering does not have any physical meaning. However, its main advantage is that it gives a regional component of the gravity or magnetic field similar to the one obtained from a graphical separation.Research Highlights? Use of non-linear filtering for regional–residual separation of potential fields. ? Examples of applications to magnetic and gravity data. ? Regional–residual separation has no unique solution. ? In practice, geological constraints should be included.
中国重力异常的小波变换与多尺度分析
[J].阐述了小波变换及多尺度分析方法的原理,利用二维小波多尺度分析方法对中国布格重力异常进行了分解,并从其中划分出有意义的剩余异常.模型结果证明方法有效.由于本文方法可以将重力异常分解成各种几何尺度意义下的不同成分,这为重力解释和研究地壳的结构提供更多更新的依据.
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary tiem series analysis
[J].DOI:10.1098/rspa.1998.0193 URL [本文引用: 1]
二维经验模式分解及其在位场去噪和分离中的应用
[J].由于实际工作中测量的位场数据存在混叠效应,并且这些观测数据具有多源性、非线性和非稳态性的特点,如何从其中提取研究对象所产生的异常信息是位场数据处理中的关键环节.二维经验模态分解(Bidimensional Empirical Mode Decomposition,BEMD)在处理非线性、非平稳信号方面具有明显的优势,且具有分解的自适应性,实现了对信号的多尺度分解.文中采用BEMD方法首先对模型试验中带噪声的重力数据进行分解,得到各级固有模态函数和剩余分量,去掉一个或多个固有模态函数实现初步去噪,或结合小波阈值实现准确、圆滑去噪;再次,对三峡地区的布格重力异常进行了多尺度分解,并且利用径向对数功率谱分析方法估计了各级模态函数所反映的地下场源似深度,定性或半定量地解释了不同深度下的场源产生的异常,较好地揭示了场源赋存的地质信息,对上述分解得到的各分量进行组合叠加,重构出局部异常和区域异常,并且同常规分场方法进行了对比分析,结果表明BEMD方法能够准确、有效地实现位场的异常分离.
经验模式分解技术在SAR干涉图滤波中的应用
[J].
DOI:10.3321/j.issn:1002-0470.2001.12.009
URL
[本文引用: 1]

提出了一种基于经验模态分解技术的滤波算法。该算法可以把原始数据分解成不同尺度的信息 ,从初始干涉图上减去与斑点噪声所对应尺度的信息 ,就可以达到斑点噪声抑制的目的。与另外两种滤波算法进行比较的结果表明 ,该算法不仅能有效地去除斑点噪声 ,并且能很好地保持相位的细节信息和条纹的边缘信息 ,保持相位的纯洁性 ,而且大比例地减少了残余点的数量 ,更有利于相位解缠。
Joint application of a statistical optimization process and empirical mode decomposition to magnetic resonance sounding noise cancelation
[J].DOI:10.1016/j.jappgeo.2014.09.023 URL [本文引用: 1]
一种基于经验模式分解(EMD)的位场分离方法
[J].经验模态分解(EMD)是一种利用信号极值特征进行时空滤波的方法。经分解得到不同阶次固有模态函数(包含从高到低不同频率段的成分),而残余量为信号的趋势分量,代表信号的平均趋势。本文将经验模态分解用于地球物理场的位场分解中,提出了一种基于EMD的位场分离方法。与常规位场分离方法中的滑动平均法和趋势分析法相比,EMD无须预先设置参数,因而不受人为因素的影响,其结果能够更好地反映位场的固有特征。应用该法对新疆准噶尔盆地准东地区的磁异常资料进行处理,从中识别出与石炭系油气有关的火成岩异常。
The empirical mode decomposition (EMD), a new tool for potential field separation
[J].Abstract: In this paper we are proposing the use of the Empirical Mode decomposition method as a tool for potential field data separation. The empirical mode decomposition (EMD) is a new data analysis method suitable to process non-stationary and nonlinear data. Its power to filter and decompose data has earned it a high reputation in signal processing. Its decomposition results in what is called "Residual", which is similar to the regional anomaly of a potential field data. This residual does not require any preset parameters unlike contemporary field separation methods. The method is applied to a magnetic data from the Jianshandian mine in Hubei, China enabling us to construct a 2.5D inverse model inferring the existence of deep ore deposits. The method is effective at separating both local and regional data from magnetic data. [Journal of American Science 2010;6(7):183-187]. (ISSN: 1545- 1003)..Keywords: Empirical Mode decomposition (EMD), Intrinsic Mode Functions (IMF), potential field separation,Jianshandian Mine
Study on application of bidimensional empirical mode decomposition in processing geophysical and geochemical data
[J].
Extracting magnetic anomalies based on improved BEMD method: a case study in the Pangxidong area, south China
[J].
基于EMD去噪方法研究及其在地质勘探中的应用
[J].
DOI:10.11720/j.issn.1000-8918.2013.3.29
URL
[本文引用: 1]

论述了EMD分解的基本原理,研究了利用EMD分解进行信号去噪的方法。EMD把信号按照不同的特征尺度分解为不同频带的IMF分量,将含有噪声的高频IMF分量剔除,选择低频或者指定频带的IMF进行信号重构,即可达到去噪的目的。仿真信号与实测数据的处理结果都表明,该方法不但有效地去除信号中的确定性噪声和随机噪声,而且尽可能地保持了有效信号,减少了信号损失,提高了数据处理的准确性。
A b-spline approach for empirical mode decompositions
[J].DOI:10.1007/s10444-004-7614-3 URL [本文引用: 1]
Statistical models for interpreting aeromagnetic data
[J].DOI:10.1190/1.1440092 URL [本文引用: 1]
Spectral analysis of gravity and magnetic anomalies due to two-dimensional structures
[J].DOI:10.1190/1.1440593 URL [本文引用: 1]
Relationship between characteristicsofgravityandmagneticanomalies and the earthquakes in the Longmenshan range and adjacent areas
[J].