利用航磁重复线测量内符合精度消除航磁梯度测量中的转向差

图1 固定翼及吊舱式航磁总场梯度测量系统的四面体结构示意

但几乎所有的高灵敏度光泵磁力仪都有一个很小的转向差。另外不同的探头由于出厂批次不同,它们之间也往往会存在一个很小的接近于常数的差值,这在ΔT测量中往往表现为不同测线之间的水平高低,ΔT测量可以采用滤波或人工方法进行调平。但利用这样的探头组成梯度系统测量结果将出现明显的正负条带,并且作为向量测量,在进行姿态改正^[10]前就需要把这个差值去掉或降到最小,否则在进行姿态改正时转向差会作为某一个方向的梯度值分配到其他方向上去。处理梯度转向差在以往的航磁梯度测量中采用了不同的方法,例如在吊舱式垂直梯度测量系统中使用操纵装置根据测线方向改变探头的方向,使探头永远保持在一个方向上^[20]。固定翼航磁梯度测量在处理干扰场造成的转向差时则将补偿系数由原来的18项改为19项,即增加一个常数项,并在计算补偿参数时使用带宽更大的滤波器^[21]。

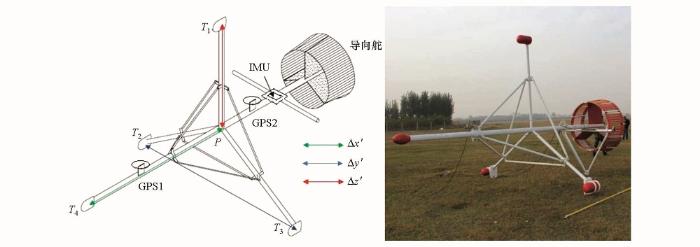
这里以中国冶金地质总局地球物理勘查院设计的直升机吊舱航磁梯度系统采集的数据进行计算。该系统集成了高精度磁力仪与双GPS/惯导测姿系统,能够完成磁总场及其3个轴向梯度的同时测量并完成姿态改正。直升机吊舱航磁梯度测量系统设计理论图及实物图如图2所示。该梯度系统在四面体4个角点各装一个探头测量磁场分别为T₁、T₂、T₃、T₄。其中1、2和3号探头构成等边三角形,P点为正三角形中心位置,在此装置下P点磁场值T_P可以通过求1、2和3号探头平均值求得:

(15) $T_{P} = \frac{T_{1} + T_{2} + T_{3}}{3} 。$

图2

图2 直升机吊舱航磁梯度系统理论图及作业实物

主杆前端装有4号探头。吊舱梯度系统测得的三轴梯度计算公式为:

(16) $\frac{\partial T}{\partial x'} = \frac{T_{4} - T_{P}}{Δ x'}, \frac{\partial T}{\partial y'} = \frac{T_{2} - T_{3}}{Δ y'}, \frac{\partial T}{\partial z'} = \frac{T_{P} - T_{1}}{Δ z'},$

其中: x'、y'、z'分别为纵向、横向、垂向;Δx'、Δy'、Δz'分别为纵向距、横向距、垂向距。

主杆上装有双GPS/INS姿态测量系统,可实时记录吊挂装置的航向角ψ,俯仰角θ和横滚角γ以及吊挂装置的坐标。梯度计算方法如下^[18,19]:

(17) $(\begin{array}{l} \frac{\partial T}{\partial x} \\ \frac{\partial T}{\partial y} \\ \frac{\partial T}{\partial z} \end{array}) = (\begin{array}{l} \cos ψ \cdot \cos θ & \cos ψ \cdot \sin θ \cdot \sin γ - \sin ψ \cdot \cos γ & \cos ψ \cdot \sin θ \cdot \cos γ + \sin ψ \cdot \sin γ \\ \sin ψ \cdot \cos θ & \sin ψ \cdot \sin θ \cdot \sin γ + \cos ψ \cdot \cos γ & \sin ψ \cdot \sin θ \cdot \cos γ - \cos ψ \cdot \sin γ \\ - \sin θ & \cos θ \cdot \sin γ & \cos θ \cdot \cos γ \end{array}) (\begin{array}{l} \frac{\partial T}{\partial x'} \\ \frac{\partial T}{\partial y'} \\ \frac{\partial T}{\partial z'} \end{array})$

其中: $\frac{\partial T}{\partial x'}$ 、 $\frac{\partial T}{\partial y'}$ 、 $\frac{\partial T}{\partial z'}$ 为式(16)中计算得到的纵向、横向和垂向梯度。 $\frac{\partial T}{\partial x}$ 、 $\frac{\partial T}{\partial y}$ 、 $\frac{\partial T}{\partial z}$ 为北方向x、东方向y和垂直z方向的梯度。ψ、θ、γ分别为姿态仪输出的航向角、俯仰角和横滚角。

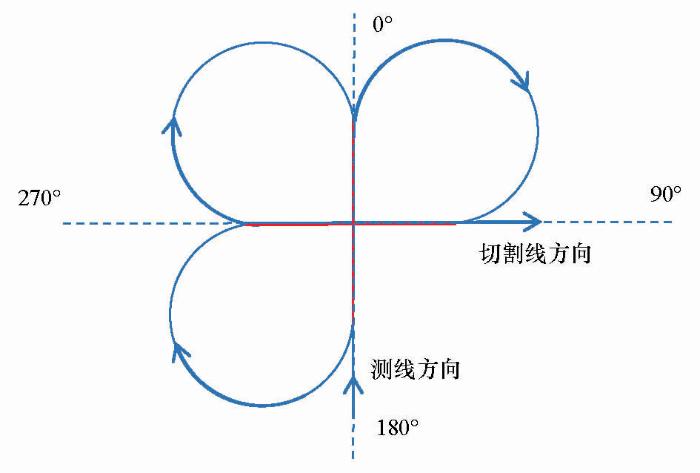
由于吊舱系统本身不需要磁补偿,为了消除梯度的转向差采用了在磁场均匀的高空(可以认为没有梯度异常)飞一个“三叶草”的方法。考虑测线与切割线的往返飞行,“三叶草”中的红色十字分别沿测线和切割线方向。梯度测量采用的多探头方法本身使得任一条测线都成为不同探头测量的同向重复线,中间的十字实际又构成梯度测量两条反向重复线。利用航迹为红色十字(图3)的数据就可以计算各个探头在4个方向上(0°,90°,180°和270°)的转向差,并评价梯度测量系统的精度。

图3

图3 飞一个“三叶草”

利用式(13)和式(6)计算水平调整前每个探头在各个方向和所有方向上的内符合精度ε_j以及所有探头的内符合总精度ε,可以见表1(因为要进行水平调整,表1中的部分数值加以负号表示水平调整的真实量。其余各表中的数值均省略了正负号)。

表1 水平调整前各探头内符合精度及总精度

	1号探头/nT	2号探头/nT	3号探头/nT	4号探头/nT
0°	-0.5285307687156141	-0.5938423666072024	0.8312815518393176	0.2915311642938796
90°	-0.5197623966896682	-0.4403397154612402	0.6405934027202965	0.3195007208107127
180°	-0.5899086526369078	-0.3399342043794137	0.9924406460766684	-0.0667719429119522
270°	-0.4991288138970681	-0.5046416770417679	0.8685583314799767	0.1353263612624347
内符合精度	0.5361862509490541	0.4868373698971536	0.846155953833143	0.2321164915774039
总精度	0.656852161018662

根据表1中每个探头在各方向上的水平调整量对每个探头进行水平调整,调整后每个探头内符合精度及总精度见表2,可以发现水平调整是非常有效的。另外还可以发现调整后总精度的值是大于每个探头的内符合精度的,这也是符合仪器的精度理论的。而如果按式(1)计算,内符合总精度将总是介于各探头的内符合精度最大值和最小值之间。实际上我们甚至可以在一定程度上将其作为水平调整一个量化指标,即(k>2时)调整后的总精度值要应大于每次观测的内符合精度值。

表2 水平调整后各探头内符合精度及总精度

	1号探头/nT	2号探头/nT	3号探头/nT	4号探头/nT
0°	0.015297704698418	0.0101696822821069	0.0158698308324947	0.018645771890485
90°	0.0066471146271898	0.0139827153611879	0.0079991965992842	0.0114905530037505
180°	0.0104115538219807	0.0271337880464745	0.0300916472247034	0.0213083517338155
270°	0.0074237272896437	0.0147040325161841	0.0111155589450553	0.009196504666883
内符合精度/nT	0.0109952508728542	0.0174781550540096	0.018523947143738	0.0163486573986367
总精度/nT	0.0185902901391291

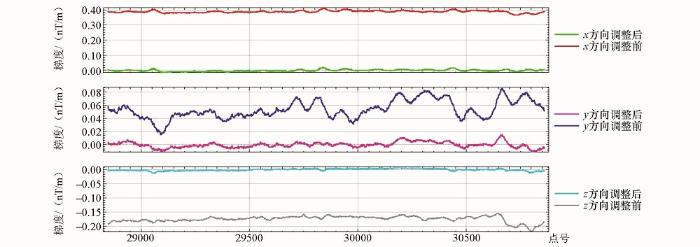
限于篇幅只对一个方向(270°)的三方向梯度进行展示,见图4。从图中可以明显的看出,调整前的梯度偏离零值,存在明显的转向差。调整后的梯度值都回到了零线上。

图4

图4 调整前与调整后的梯度三分量

调整后的三方向梯度值可以认为完全是梯度系统的噪声(包括磁力仪和姿态仪的噪声),计算其均方差得到表3。作者认为这样计算的噪声水平要比利用在地面测量的静态数据计算的噪声更能反映梯度系统在测量过程中的动态水平,也比利用全区测量数据的四阶差分均方差计算的动态噪声更合理。

表3 梯度的噪声统计

	x方向梯度/(pT/m)	y方向梯度/(pT/m)	z方向梯度/(pT/m)
0°	7.918254073475	5.269886898420	6.386599562450
90°	5.618693071148	4.737651809021	2.750794712067
180°	9.126889912194	14.280973532021	5.173281582975
270°	5.897774739030	4.261252718721	3.964132836451
总噪声水平/(pT/m)	7.400698472359	8.246677420401	4.935249534654

如果忽略掉姿态仪的噪声,即将ψ=0°、90°、180°、270°和θ=γ=0直接代入式(17)后得到的梯度值计算噪声水平,结果可见表4。比较表3和表4可以看出噪声整体变化不大,说明姿态仪的噪声水平是比较低的。另外本次标定飞行中姿态改正实际上将各探头组成的梯度系统z方向梯度的噪声向x和y方向的梯度进行了转移分配。

表4 梯度的噪声统计

	x方向梯度/(pT/m)	y方向梯度/(pT/m)	z方向梯度/(pT/m)
0°	7.891094367541	5.353451252041	6.354018188118
90°	5.485889672940	4.864836034794	2.795427426588
180°	8.974530273678	14.203122283713	5.623773726930
270°	6.088297048451	3.891321292421	4.057542818538
总噪声水平/(pT/m)	7.358282103413	8.205021353050	5.065314631441

从图2和表3可以看出,由于计算y方向梯度只使用了2和3号探头,其噪声是比较大的。尤其是在180°方向上,y方向的梯度噪声超过了14 pT/m,而x方向和z方向梯度,由于使用到了1、2和3号探头的均值,使其噪声明显降低。因此利用四面体4个角点的几何关系计算梯度时充分发挥每个探头的空间贡献^[13]在很大程度上可以降低梯度系统的噪声水平,从这个意义来说正四面体结构不失为一种更好的选择,但梯度的计算式(15)~(17)也会更加复杂。

同时也可以计算测线与切割线方向构成的两条反向重复线的内符合精度作为参考,根据徐东礼^[8]提出的在特定方向上取最近点匹配的方法,由于只有一条重复线因此可以直接用式(12)计算,得到的内符合精度见表5和表6。

表5 水平调整前梯度各方向分量的内符合精度

	x方向梯度/(pT/m)	y方向梯度/(pT/m)	z方向梯度/(pT/m)
测线方向	47.2734597845345	559.6277155395362	59.6560139466257
切割线方向	493.8845107917437	118.7910771059847	8.1289605731606
总内符合精度/(pT/m)	340.9212225720188	414.8794885264877	43.7203613891743

表6 水平调整后梯度各方向分量的内符合精度

	x方向梯度/(pT/m)	y方向梯度/(pT/m)	z方向梯度/(pT/m)
测线方向	5.9732738092272	10.9558203709261	4.2848570571257
切割线方向	5.1516987489565	4.7507894080879	2.8035691537752
总内符合精度/(pT/m)	5.6008927859762	8.6058119895801	3.6619666847201

必须指出的是多探头组成的梯度系统由于各个探头随姿态变化其空间转向差变化也不同,探头两两之间的差值也造成了梯度系统的空间转向差,以上方法只是考虑在四个方向上的不同,并没有考虑梯度系统在全空间内的转向差。这类似最早的航磁干扰场补偿中补偿恒定场的方法。

4 结论

对于重、磁勘探规范中各种计算公式进行细致的解读,从本质上理解数理统计方法评价重、磁勘探中仪器的工作性能和整个测量工作的精度具有实际意义。笔者将航磁重复线内符合精度计算公式进行了改进,使其和地面重磁勘探中仪器一致性、质量检查精度计算及航空重磁测量中利用测线与切割线交叉点计算总精度具有形式上的统一。将其应用于梯度测量中消除梯度的转向差和评价航磁吊舱梯度测量系统的测量精度上,并对吊舱式航磁总场梯度测量系统的改进提出了具有建设性的建议。对于航磁梯度测量的研究正如火如荼,望批评指正。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Z/T 0071-1993地面高精度磁测技术规程

[S]. 北京: 中国标准出版社, 1993.

[2]

Y/T 5771-2011地面磁法勘探技术规程

[S]. 北京: 石油工业出版社, 2011.

[本文引用: 1]

[3]

Z/T 0082-1993区域重力调查规范

[S]. 北京: 中国标准出版社, 1993.

[本文引用: 1]

[4]

DZ/T0142-2010航空磁测技术规范[S]

北京: 中国标准出版社, 2010.

DOI:10.3969/j.issn.1000-0658.2009.06.006 URL [本文引用: 1]

[5]

郭志宏, 熊盛青, 周坚鑫 , 等.

航空重力重复线测试数据质量评价方法研究

[J]. 地球物理学报, 2008,51(5):1538-1543.

DOI: Magsci [本文引用: 2]

为了量化评估航空重力系统的性能指标，通常采用多次往返的重复线测量方式来测试航空重力仪动态测量的重复性和一致性，但现有规范中没有明确针对航空重力重复线测试数据质量的评估准则，本文研究总结了航空重力重复线测试数据均方差精度计算方法，依据重复线测试数据均方差内、外符合精度的计算结果，可以更为客观地评估仪器的动态测量精度指标和工作状态.

[6]

姜作喜, 张虹, 郭志宏 .

航空重力测量内符合精度计算方法

[J]. 物探与化探, 2010,34(5):672-676.

URL Magsci [本文引用: 1]

为了评估航空重力系统的性能指标，通常采用对一条测试线多次往返飞行计算各条重复测试线内符合精度的方法。笔者研究了一种较准确的计算各重复线对应点的方法，并在对应点处采用插值方法计算其重力值，利用重复线上对应点的重力值进行均方差计算可以得到精度较高的内符合精度值。

[7]

徐东礼, 骆遥, 贾伟洁 .

航磁重复线测量数据质量评价方法研究

[J]. 物探与化探, 2014,38(4):729-731.

DOI:10.11720/wtyht.2014.4.17 URL Magsci [本文引用: 1]

为了量化评估航磁测量系统的动态性能指标，通常采用多次往返的重复线测量方式，来测试系统的工作稳定性和一致性，但现有规范中对重复线测量数据质量没有明确的量化标准，笔者对造成重复线磁场测量值偏差的原因进行了客观的分析，研究总结了航磁重复线测量数据均方差精度计算方法，并编写了相应的计算软件，依据重复线测量数据均方差内符合精度计算结果，客观地评估仪器的动态测量精度指标和工作状态。

[8]

徐东礼, 叶挺明, 舒晴 , 等.

航磁重复线内符合精度计算方法

[J]. 物探与化探, 2016,40(1):125-128.

DOI:10.11720/wtyht.2016.1.22 Magsci [本文引用: 2]

为了评价航磁测量数据的质量,通常采用重复线飞行,计算重复线测量值均方差内符合精度的评价方法,而计算内符合精度,最重要的是准确建立测线和重复线公共线段上的对应测点。笔者研究并采用了最小距离法,计算测线和重复线公共线段上测点对应关系,经过位置改正、磁场水平调整等处理,完成重复线上对应点测量值均方差的计算,获得准确的内符合精度计算结果。

[9]

盛骤, 谢式千, 潘承毅 .

概率论与数理统计(浙大,第三版)

[D]. 北京: 高等教育出版社, 2001.

[本文引用: 1]

[10]

李晓禄, 蔡文良 .

运五飞机上航磁梯度测量系统的安装与补偿

[J] . 物探与化探, 2006,30(3) : 224-228.

DOI:10.3969/j.issn.1000-8918.2006.03.009 URL Magsci [本文引用: 2]

介绍了在单阀双翼的运五飞机上安装既可进行垂直梯度测量,又可进行水平梯度测量(包括横向和纵向水平梯度测量)的航磁梯度测量系统的方法,初步探讨应用航空地球物理综合测量系统(AADCⅡ)自动航空磁力数字补偿仪的方法,并对补偿结果进行评价。多次实验结果证明了该补偿方法的效果良好。

[11]

李晓禄, 常树帅 .

航磁梯度测量及其在砂岩型铀矿勘查中的应用初探

[J]. 铀矿地质, 2009,25(6):355-360.

简单介绍了航磁梯度测量的方法原理、优点及数据处理技术,并将该方法应用于砂岩型铀矿勘查中,对浅层断裂的识别、铀成矿环境的识别及磁性层体埋藏深度反演等方面进行了初步探讨,认为航磁梯度测量可在砂岩型铀矿勘查中发挥重要作用.

[12]

骆遥, 段树岭, 王金龙 , 等.

AGS-863航磁全轴梯度勘查系统关键性指标测试

[J] . 物探与化探, 2011,35(5) : 620-625.

URL Magsci [本文引用: 1]

中国国土资源航空物探遥感中心成功研制出具有完全自主知识产权的AGS-863航磁全轴梯度勘查系统,并在内蒙古某地进行了航磁全轴梯度试生产。为配合航磁全轴梯度试生产,对系统设计的关键性指标予以实际测试,设计了相关试验,以验证AGS-863航磁全轴梯度勘查系统的稳定性与可靠性。测试结果表明系统具有非常好的同步特性、一致性和长期稳定性以及补偿精度。

[13]

张青杉, 麻丰林, 许丽云 .

航空三维磁梯度测量方案研究

[J] . 地质与勘探, 2010,46(6):1087-1091.

URL [本文引用: 2]

本文概略介绍了航空三维磁梯度测量的发展现状,指出了实施航空三维磁梯度测量所应着力解决的几个问题,包括基本装置及其计算方法、探头一致性、探头姿态以及固定翼磁补偿问题等,并针对当前状况提出了用于大比例尺或中-大比例尺航空三维磁梯度测量的具体方案,大胆引入了正四面体测量装置,并将陀螺仪数据同步至原航测数据之中,既可大幅度提高测量精度及数据稳定性,同时可解决同点三梯度的数值计算问题,对后续数据处理、成图、解释均具有重要意义。

[14]

郭华, 王平, 谢汝宽 .

航磁全轴梯度数据地质解释优势研究

[J]. 地球物理学进展, 2013,28(5):2688-2692.

DOI:10.6038/pg20130551 URL Magsci [本文引用: 1]

中国国土资源航空物探遥感中心成功研制出具有完全自主知识产权的航磁全轴梯度勘查系统,在中国的北部某地区进行了航磁全轴梯度测量飞行,获得了横向梯度、纵向梯度和垂向梯度数据.本文简要介绍了测区地质概况、飞行方案及数据处理等,重点对梯度数据在断裂构造划分等方面进行了探讨,认为航磁梯度数据比总场数据更加清晰显示构造走向,并比较了实测和转换的垂向梯度数据,结果表明实测垂向梯度在反映地质体边界等方面具有一定优势.

[15]

郭华, 贾伟洁, 王平 , 等.

航磁梯度数据在磁性地质体边界判断方面的研究

[J]. 吉林大学学报:地球科学版, 2015,45(1):273-281.

DOI:10.13278/j.cnki.jjuese.201501301 URL [本文引用: 1]

完全国产化的航磁全轴梯度勘查系统已开展了测量工作,并获得了比较理想的梯度数据,但是如何利用梯度数据进行磁性地质体边界圈定还处于研究阶段。笔者先给出了航磁全轴梯度测量原理;然后着重从利用梯度数据尤其是垂向梯度数据进行岩体边界圈定等方面进行了讨论研究,认为航磁梯度数据相比于总场数据在地质体边界判断方面可提供更加丰富的地球物理信息;接着提出了梯度数据需要在判断磁性地质体边界上进行化极处理,并根据垂向梯度数据零值线确定地质体边界的原则,圈定磁性地质体的边界位置。与实际地质情况的对比表明,利用梯度数据圈定磁性地质体边界的应用效果比利用总场数据的效果明显。

[16]

郭华, 吴成平 .

航磁梯度数据与地质异常反映之间的关系

[J]. 地球物理学进展, 2014,29(4):1650-1656.

DOI:10.6038/pg20140421 URL Magsci [本文引用: 1]

在异常选编工作中，往往需要剔除掉区域背景场的干扰，从而寻找浅部异常的一些信息，因为区域背景场往往是由一些火山岩、侵入岩所引起，当然也不排除大型矿床所引起的可能性，航磁总场是区域场和局部场的叠加，因此异常往往会因为某种方式被忽略掉.梯度数据具有压制深部异常体、突出浅部异常体信息的特点，这就为梯度数据能够方便地提取异常提供了理论支持.在中国的北部某地区进行了航磁全轴梯度测量飞行，获得了横向梯度、纵向梯度和垂向梯度数据，利用实测数据总结出梯度数据与地质体异常之间的关系，确定了异常选编原则，为今后梯度数据确定异常奠定了基础，同时分析了实测的垂向梯度数据相比于转换的垂向梯度数据在异常反映上信息更丰富.

[17]

安战锋, 王平, 段树岭 , 等.

国产航磁全轴梯度勘查系统试验测量

[J]. 物探与化探, 2016,40(2):370-373.

DOI:10.11720/wtyht.2016.2.22 Magsci [本文引用: 1]

2009年7月,"全数字化矢量航磁勘查系统研发"课题组在哈尔滨平房机场对航磁全轴梯度勘查系统样机实施系统试验测试及试验测量,先后进行了飞机改装、系统集成测试、补偿飞行及约5000km的试验测量飞行,取得了良好的效果,表明该系统样机性能稳定可靠,初步达到实用化程度,实验工作为今后系统的改进与完善提供了依据。

[18]

梁建, 郭玉峰, 纪福山 , 等.

直升机吊舱航磁全轴梯度测量系统在新疆哈密地区的应用

[J]. 工程地球物理学报, 2017,14(2):192-198.

[19]

梁建

航磁梯度测量姿态变换研究及应用

[D] . 北京:中国地质大学(北京) , 2016.