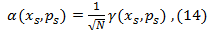天然气水合物储层弹性波最小二乘逆时偏移研究

引用本文

李金丽, 曲英铭, 刘建勋, 岳航羽, 李培, 陈德元. 天然气水合物储层弹性波最小二乘逆时偏移研究[J]. 物探与化探, 2017,41(6): 1050-1059.
LI Jin-Li, QU Ying-Ming, LIU Jian-Xun, YUE Hang-Yyu, LI Pei, CHEN De-Yuan. A study of elastic least-squares reverse time migration for gas hydrate reservoirs[J]. Geophysical and Geochemical Exploration, 2017,41(6): 1050-1059.
Doi:10.11720/wtyht.2017.6.09 复制到剪切板

Permissions

#cod#x00A9; 《物探与化探》编辑部

天然气水合物储层弹性波最小二乘逆时偏移研究

李金丽^1,², 曲英铭³, 刘建勋^1,², 岳航羽^1,², 李培^1,², 陈德元^1,²

1.国家现代地质勘查工程技术研究中心,河北廊坊 065000

2.中国地质科学院地球物理地球化学勘查研究所,河北廊坊 065000

3.中国石油大学(华东) 地球科学与技术学院,山东青岛 266580

作者简介: 李金丽(1989-),女,硕士研究生,主要从地震数据处理及偏移成像方面的研究工作。

收稿日期: 2017-09-08

基金: 国家高技术研究发展计划(“863”计划)课题(2012AA061403); 中国地质调查局地质调查项目(DD20160224); 中央级公益性科研院所基本科研业务费专项基金资助项目(AS2017J11)

摘要

天然气水合物的弹性性质相比于周围岩层有明显的差异。传统声波成像方法采用声波近似,无法对其弹性性质进行准确地描述,弹性波偏移方法的成像结果分辨率低、中深部成像能量弱、振幅不均衡,存在低频噪声和采集脚印。为此,文中发展了一种弹性波最小二乘逆时偏移方法,在该方法中,推导了准确的弹性波最小二乘理论框架下的偏移算子和反偏移算子。为了提高计算效率并节省内存,引入了基于编码技术的混叠数据弹性波最小二乘方法,将多炮数据叠加为一个超道集,并采用编码技术压制串扰噪声。通过对两个含天然气水合物模型的试算验证了本文方法对天然气水合物储层成像的有效性及优越性。

关键词: 天然气水合物; 弹性波; 最小二乘逆时偏移; 编码

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2017)06-1050-10

A study of elastic least-squares reverse time migration for gas hydrate reservoirs

LI Jin-Li^1,², QU Ying-Ming³, LIU Jian-Xun^1,², YUE Hang-Yyu^1,², LI Pei^1,², CHEN De-Yuan^1,²

1.National Modern Geological Exploration Technology Research Center,Langfang 065000,China

2.Institute of Geophysical and Geochemical Exploration,Chinese Academy of Geological Sciences,Langfang 065000,China

3.School of Geosciences,China University of Petroleum (East China),Qingdao 266580,China

Abstract

The elastic properties of gas hydrate are obviously different from those of the surrounding rocks.The traditional acoustic imaging method using acoustic approximation cannot accurately describe the elastic properties.The imaging results of elastic wave migration method have low resolution,weak energy in deep regions,imbalance amplitude, low frequency noise and acquisition footprint.For this reason,the authors have developed an elastic least-squares inverse time migration method.In this method,an accurate migration operator and demigration operator in the framework of the elastic least squares theory are derived.To improve the computation efficiency and save memory,the authors introduced the multisource elastic least-squares migration method based on encoding technique,in which multiple data are added into a supershot and the encoding technique is used to suppress the crosstalk.The effectiveness and superiority of the proposed method for gas hydrate reservoir imaging are verified by the simulation results of two gas hydrate models.

Keyword: gas hydrate; elastic; least-squares reverse time migration; encoding

Show Figures

0 引言

天然气水合物最早发现于20世纪40年代末, 又被称为“ 可燃冰” 或者“ 固体瓦斯” , 分布于多年的冻土区沉积物或者高孔隙流体压力和低温条件下的深海沉积物中^[1], 是由水和天然气在低温高压条件下形成的冰状固体物质^{[2, 3]}。近年来, 天然气水合物得到了广泛的研究和重视主要因为以下两点原因:①天然气水合物储量丰富, 全球共有大约7× 10⁵万亿ft³的甲烷储藏于天然气水合物中^[4], 与其他化石燃料的储量相当^[5]; ②天然气水合物中甲烷含量超过80%, 因此天然气水合物污染小^[6]。对天然气水合物物性的研究主要可以分成实验室测量^[7]、直接提取岩心^[8]及地震反射特征研究^[9]。通过对天然气水合物的物性研究, 其纵波速度、横波速度以及密度都得到了明确的估计。徐明才等指出冻土区破碎带中含天然气水合物的地层具有较低的纵横波速度、密度及泊松比^{[10, 11]}。Akihisa等对天然气水合物的物理参数特性进行了概括总结^[12]。

地震勘探对于探明天然气水合物储层也发挥着越来越重要的作用。通过偏移技术, 可以对地下复杂构造进行成像。传统偏移方法大多数都是采用正演算子的共轭来代替它本身的逆^{[13, 14]}, 也就是说, 传统偏移方法可以准确地处理运动学信息, 但是成像剖面的振幅无法准确地反映反射系数, 这将会导致一系列成像问题, 例如低频噪声、低信噪比、成像振幅不均衡及采集脚印等^[15]。最小二乘偏移方法是一种线性反演方法, 该方法可以提高成像剖面的分辨率并压制偏移噪声, 可以得到真振幅剖面^[16]。在国内, 最小二乘偏移虽然比国外晚一些, 但是该方法也得到了大量的研究。2008年, 杨其强等实现了基于傅里叶有限差分偏移算子的叠后最小二乘偏移, 很好地克服了传统偏移方法的缺点, 获得了高分辨率的成像剖面^[17]。2010年, 罗国安等实现了一种快速的叠前最小二乘偏移算法, 该算法是基于均匀介质假设下提出的, 因此虽能在一定程度上改善成像质量, 但在复杂介质上存在一定的问题^[18]。2013年, 黄建平将最小二乘逆时偏移(LSRTM)算法应用到碳酸盐岩成像方法中, 但并没有应用于天然气水合物的成像中^[19]。2014年, 黄建平等对近地表复杂构造进行了成像研究, 同时还指出了最小二乘逆时偏移在近地表成像方面所具有的独特优势^[20]。2015年, 刘玉金和李振春基于最小二乘理论和算法提出了一种扩展成像条件下的成像方法, 能够在初始速度模型存在一定误差的情况下获取真振幅的LSRTM成像结果^[21]。同年, 郭书娟将LSRTM理论应用到实际资料中, 建立了LSRTM成像流程^[22]。

前述的LSRTM方法是基于声波近似的单分量地震数据, 没有利用多分量信息, 而多分量地震勘探因其可以充分利用纵横波及转换波信息, 所以可以对地下构造进行更准确的成像^{[23, 24, 25]}, 而弹性波成像方法能够充分利用多分量地震数据, 因此近年来弹性波逆时偏移成像方法得到了推广应用^[26], 但弹性波逆时偏移仍然存在如上文介绍的传统偏移方法的缺点, 无法得到精确的成像。为了对天然气水合物储层进行精确的成像, 文中发展了一种弹性波最小二乘逆时偏移方法, 并将其应用到天然气水合物勘探中, 通过对三层天然气水合物模型和复杂天然气水合物模型的试算, 来验证本文方法的准确性。

1 弹性波最小二乘逆时偏移基本原理

1.1 最小二乘逆时偏移理论

最小二乘偏移可以看作是一种解决最优化反演问题的方法。目的是通过最小化目标函数

$\begin{matrix} \begin{matrix} E (m) = \frac{1}{2} ‖ d_{cal} - d_{obs} ‖_{2}^{2} = \frac{1}{2} ‖ Lm - d_{obs} ‖_{2}^{2} \to \min (1) \end{matrix} \end{matrix}$

来寻找最小二乘意义上的扰动模型以拟合观测数据。其中:d_cal和d_obs分别表示模拟数据和观测数据, 模拟数据表示为d_cal=Lm, 其中L表示正演模拟算子, m是反射系数模型。在文中, 我们使用预条件的共轭梯度法^[27]来解决最小二乘反问题。共轭梯度法使用公式

$\begin{matrix} m^{(k + 1)} = m^{(k)} - β^{(k)} d k^{(k)} (2) \end{matrix}$

求取反射系数模型。其中:m⁽^k⁾和m⁽^k+¹⁾表示第k次和(k+1)次反射系数模型; dk⁽^k⁾和β ^k为k次迭代的梯度方向和步长, 它们由4个公式求得:

$g^{(k)} = L^{T} [L m^{(k)} - d_{obs}] (3)$

$α^{(k)} = \frac{[g^{(k)}]^{T} [C g^{(k)}]}{[g^{(k - 1)}]^{T} [C g^{(k - 1)}]} (4)$

$d k^{(k)} = C g^{(k)} - β^{(k)} d k^{(k - 1)} (5)$

$β^{(k)} = \frac{[d k^{(k)}]^{T} [Cd k^{(k)}]}{[Ld k^{(k - 1)}]^{T} [Ld k^{(k - 1)}]} (6)$

其中:g⁽^k⁾和α ⁽^k⁾为使用最速下降法得到的第k次迭代的梯度方向和步长; T为矩阵的转置; L^T是逆时偏移算子; C为预条件算子。在文中, 我们使用加权的保幅偏移方法作为预条件算子^[28]。

1.2 基于一阶速度— 应力方程的弹性波最小二乘逆时偏移理论时间域, 一阶变密度速度-应力方程可表示为:

$\begin{matrix} \{\begin{matrix} ρ \frac{\partial v_{x} (x, t)}{\partial t} = \frac{\partial τ_{xx} (x, t)}{\partial x} + \frac{\partial τ_{xz} (x, t)}{\partial z}, \\ ρ \frac{\partial v_{z} (x, t)}{\partial t} = \frac{\partial τ_{xz} (x, t)}{\partial x} + \frac{\partial τ_{zz} (x, t)}{\partial z}, \\ \frac{\partial τ_{xx} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial v_{x} (x, t)}{\partial x} + λ \frac{\partial v_{z} (x, t)}{\partial z} + f_{x} (x, t), \\ \frac{\partial τ_{zz} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial v_{z} (x, t)}{\partial z} + λ \frac{\partial v_{x} (x, t)}{\partial x} + f_{z} (x, t), \\ \frac{\partial τ_{x z} (x, t)}{\partial t} = μ (\frac{\partial v_{x} (x, t)}{\partial z} + \frac{\partial v_{z} (x, t)}{\partial x}) 。 \end{matrix} (7) \end{matrix}$

其中:v_x和v_z分别为水平分量和垂向分量的速度, τ _xx和τ _zz为正应力, τ _xz为切应力, f_x和f_z为震源项, t是计算时间, x表示空间坐标(x, z), ρ 为密度, λ 和μ 是Lamé 参数。Lamé 参数λ 和μ 、密度ρ 、P波速度v_p、S波速度v_s的关系为:

$\begin{matrix} \{\begin{matrix} λ = ρ (v_{p}^{2} - 2 v_{s}^{2}), \\ μ = ρ v_{s}^{2} 。 \end{matrix} (8) \end{matrix}$

基于伯恩近似, 波场的扰动可由下面的反偏移公式求得(见附件A):

$\{\begin{matrix} ρ_{0} \frac{\partial v_{x 0} (x, t)}{\partial t} = \frac{\partial τ_{xx 0} (x, t)}{\partial x} + \frac{\partial τ_{xz 0} (x, t)}{\partial z}, \\ ρ_{0} \frac{\partial v_{z 0} (x, t)}{\partial t} = \frac{\partial τ_{xz 0} (x, t)}{\partial x} + \frac{\partial τ_{zz 0} (x, t)}{\partial z}, \\ \frac{\partial τ_{xx 0} (x, t)}{\partial t} = (λ_{0} + 2 μ_{0}) \frac{\partial v_{x 0} (x, t)}{\partial x} + λ_{0} \frac{\partial v_{z 0} (x, t)}{\partial z} + f_{x} (x, t), \\ \frac{\partial τ_{zz 0} (x, t)}{\partial t} = (λ_{0} + 2 μ_{0}) \frac{\partial v_{z 0} (x, t)}{\partial z} + λ_{0} \frac{\partial v_{x 0} (x, t)}{\partial x} + f_{z} (x, t), \\ \frac{\partial τ_{xz 0} (x, t)}{\partial t} = μ_{0} (\frac{\partial v_{x 0} (x, t)}{\partial z} + \frac{\partial v_{z 0} (x, t)}{\partial x}) 。 \end{matrix} 9 a)$

$\begin{matrix} \begin{matrix} \{\begin{matrix} ρ \frac{\partial δ v_{x} (x, t)}{\partial t} = \frac{\partial δ τ_{xx} (x, t)}{\partial x} + \frac{\partial δ τ_{xz} (x, t)}{\partial z} - m (ρ) \frac{\partial v_{x 0} (x, t)}{\partial t} \\ ρ \frac{\partial δ v_{z} (x, t)}{\partial t} = \frac{\partial δ τ_{xz} (x, t)}{\partial x} + \frac{\partial δ τ_{zz} (x, t)}{\partial z} - m (ρ) \frac{\partial v_{z 0} (x, t)}{\partial t} \\ \frac{\partial δ τ_{xx} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{x} (x, t)}{\partial x} + λ \frac{\partial δ v_{z} (x, t)}{\partial z} + m (λ) (\frac{\partial v_{x 0} (x, t)}{\partial x} + \frac{\partial v_{z 0} (x, t)}{\partial z}) + 2 m (μ) \frac{\partial v_{x 0} (x, t)}{\partial x} \\ \frac{\partial δ τ_{zz} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{z} (x, t)}{\partial z} + λ \frac{\partial δ v_{x} (x, t)}{\partial x} + m (λ) (\frac{\partial v_{x 0} (x, t)}{\partial x} + \frac{\partial v_{z 0} (x, t)}{\partial z}) + 2 m (μ) \frac{\partial v_{z 0} (x, t)}{\partial z} \\ \frac{\partial δ τ_{xz} (x, t)}{\partial t} = μ (\frac{\partial δ v_{x} (x, t)}{\partial z} + \frac{\partial δ v_{z} (x, t)}{\partial x}) + m (μ) (\frac{\partial v_{x 0} (x, t)}{\partial z} + \frac{\partial v_{z 0} (x, t)}{\partial x}) \end{matrix} (9 b) \end{matrix} \end{matrix}$

其中:U₀和V₀表示背景波场和背景参数, δ U和δ V表示扰动波场和扰动参数, U=(v_x, v_z, τ _xx, τ _zz, τ _xz), V=(λ , μ , v_p, v_s, ρ )。反射系数模型定义为:

$\begin{matrix} m (V) = δV = V - V_{0} 。 (10) \end{matrix}$

根据伴随状态理论^[29], 我们给出关于λ , μ 和ρ 的梯度公式为(见附件A):

$g_{λ} = \frac{\partial E}{\partial λ} = \int ((\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) τ_{xx}^{R} + (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) τ_{zz}^{R}) dt, (11 a)$

$g_{μ} = \frac{\partial E}{\partial μ} = \int (2 \frac{\partial v_{x 0}}{\partial x} τ_{xx}^{R} + 2 \frac{\partial v_{z 0}}{\partial z} τ_{zz}^{R} + (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) τ_{xz}^{R}) dt, (11 b)$

$\begin{matrix} \begin{matrix} g_{ρ} = \frac{\partial E}{\partial ρ} = \int (- \frac{\partial v_{x 0}}{\partial t} v_{x}^{R} - \frac{\partial v_{z 0}}{\partial t} v_{z}^{R}) dt, (11 c) \end{matrix} \end{matrix}$

其中U^R为检波波场的反传, 并由下式求得:

$\{\begin{matrix} ρ \frac{\partial v_{x}^{R} (x, t)}{\partial t} = \frac{\partial τ_{xx}^{R} (x, t)}{\partial x} + \frac{\partial τ_{xz}^{R} (x, t)}{\partial z} + Δ d_{x}, \\ ρ \frac{\partial v_{z}^{R} (x, t)}{\partial t} = \frac{\partial τ_{xz}^{R} (x, t)}{\partial x} + \frac{\partial τ_{zz}^{R} (x, t)}{\partial z} + Δ d_{z}, \\ \frac{\partial τ_{xx}^{R} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial v_{x}^{R} (x, t)}{\partial x} + λ \frac{\partial v_{z}^{R} (x, t)}{\partial z} + f_{x} (x, t), \\ \frac{\partial τ_{zz}^{R} (x, t)}{\partial t} = (λ + 2 μ) \frac{\partial v_{z}^{R} (x, t)}{\partial z} + λ \frac{\partial v_{x}^{R} (x, t)}{\partial x} + f_{z} (x, t), \\ \frac{\partial τ_{xz}^{R} (x, t)}{\partial t} = μ (\frac{\partial v_{x}^{R} (x, t)}{\partial z} + \frac{\partial v_{z}^{R} (x, t)}{\partial x}) 。 \end{matrix} (12 a)$

$\{\begin{matrix} Δ d_{x} (x, t) = d_{cal, x} (x, t) - d_{obs, x} (x, t), \\ Δ d_{z} (x, t) = d_{cal, z} (x, t) - d_{obs, z} (x, t) \end{matrix} (12 b)$

$\begin{matrix} \begin{matrix} \{\begin{matrix} d_{cal, x} (x, t) = δ v_{x} (x, t), \\ d_{cal, z} (x, t) = δ v_{z} (x, t) \end{matrix} (12 c) \end{matrix} \end{matrix}$

其中:d_cal,_x和d_cal,_z分别为水平分量和垂直分量的模拟数据, d_obs,_x和d_obs,_z分别为水平分量和垂直分量的观测数据。

v_p, v_s和ρ 的梯度可由链式公式求得^[30]:

$g_{v_{p}} = 2 v_{p} ρ g_{λ}, (13 a)$

$g_{v_{s}} = - 4 v_{s} ρ g_{λ} + 2 v_{s} ρ g_{μ}, (13 b)$

$g_{ρv} = (v_{p}^{2} - 2 v_{s}^{2}) g_{λ} + v_{s}^{2} g_{μ} + g_{ρ} 。 (13 c)$

修正的v_p, v_s和ρ 的梯度方向及其对应的步长都可由式(5)、式(6)求得。在文中, 我们只利用式(13a)、(13b)求取含天然气水合物介质v_p和v_s分量的像。

1.3 编码LSRTM理论

常规弹性波最小二乘逆时偏移方法占用内存大、计算成本高。编码多震源LSRTM通过将多炮叠加到一起组成一个或者若干个超道集, 可以将弹性波最小二乘逆时偏移的计算量减少到与常规弹性波逆时偏移相当的水平, 并通过编码函数来压制多炮数据的串扰噪声^{[31, 32, 33]}。

在文中, 我们使用Liu等^[34]提出的单样本随机相移编码函数来压制不同炮记录之间的串扰噪声。编码函数定义为:

其中p_s为指数, N是迭代次数, γ 是随机符号序列, 由+1和-1组成。

2 模型试算

2.1 含天然气水合物的三层模型试算

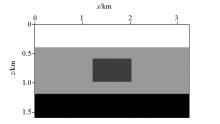
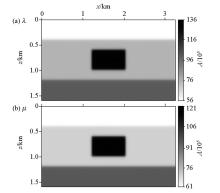
图1所示的为含天然气水合物的3层模型, 该模型中第1层表示的为上覆盖层, 中间1层中包含围岩和天然气水合物储层, 下面一层为下覆岩层。该模型的大小为3 200 m× 1 600 m, 横向采样点数为401, 纵向采样点数为201, 网格间距为8 m。该模型的物性参数如表1所示。首先, 我们采用该模型验证本文提出的弹性波伯恩近似方法。正演模拟采用的是主频为25 Hz的爆炸震源, 在(1 600 m, 8 m)处激发。总的记录长度为1.5 s, 采样间隔为0.6 ms, 双分量检波器的总数为401, 相邻检波器之间的距离为9 m。拉梅常数的反射系数和偏移模型分别由图2和图3表示。

	Figure Option View Download New Window
	图1 含天然气水合物的3层模型

表1 含天然气水合物的3层模型物性参数

	Figure Option View Download New Window
	图2 含天然气水合物的3层模型反射系数

	Figure Option View Download New Window
	图3 含天然气水合物的3层模型偏移参数

接下来, 我们使用合成炮记录对弹性波最小二乘逆时偏移成像方法进行测试。合成数据采用的观测系统为:炮集的总炮数为100炮, 均匀的分布于地表处, 检波器的总数为401。图4展示了使用弹性波最小二乘逆时偏移不同迭代次数的成像结果, 其中图4a和4b为第1次迭代的成像结果, 也就是传统弹性波逆时偏移的成像结果, 图4c和4d为第50次迭代最终的成像结果。从图中可以看出, 采用传统弹性波逆时偏移的成像结果存在明显的低频噪声, 成像能量不均衡, 分辨率较低, 深部能量弱; 采用弹性波最小二乘逆时偏移得到的成像结果, 低频噪声得到了很好的压制, 能量更加均衡, 深层的振幅得到了很好的补偿, 信噪比和分辨率明显提高, 无明显的采集脚印, 三层界面和天然气水合物储层界面清晰地成像出来, 特别是天然气水合物的高陡界面也很好地成像出来。此外, 对比v_p、v_s分量成像结果, 我们可以看出:v_s分量的成像结果比v_p分量具有更好的分辨率, 因为S波比P波的波长更短。从该模型试算我们可以得出, 文中提出的弹性波最小二乘逆时偏移算法可以更加准确地成像出天然气水合物的储层, 这对于寻找天然气水合物具有重要意义。

	Figure Option View Download New Window
	图4 使用弹性波最小二乘逆时偏移得到的第1次(a, b)和第50次(c, d)迭代的成像结果a— v_p分量; b— v_s分量; c— v_p分量; d— v_s分量

2.2 复杂天然气水合物模型

为了进一步分析文中提出的弹性波最小二乘逆时偏移方法对复杂模型的适应性, 构造了如图5所示的复杂天然气水合物弹性波模型。该模型由盐丘模型改造而成, 中间盐丘体的纵横波速度、密度分别为3 300 m/s、1 800 m/s、0.91 g/cm³, 围岩的速度和密度明显高于天然气水合物储层。从模型中也可以看出, 在天然气水合物储层的周围, 断裂构造发育明显。该复杂天然气水合物模型的大小为 5 160 m× 1 200 m, 横向采样点数为645, 纵向采样点数为150, 网格间距为8 m。固定的观测系统由107个P波震源组成, 该组震源的激发波形为25 Hz的雷克子波。弹性波合成炮记录由369个多分量检波器接收, 检波器的总数为645, 均匀地分布于地表。相邻震源间距为48 m, 相邻检波器间距为8 m。时间采样间隔为0.6 ms, 记录时间为3 s。图6为该复杂天然气水合物模型的反射系数, 它可以看作是λ 和μ 的真实成像结果。

	Figure Option View Download New Window
	图5 复杂天然气水合物模型a— v_p; b— v_s; c— ρ

	Figure Option View Download New Window
	图6 复杂天然气水合物模型的反射系数

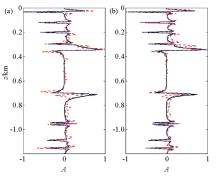
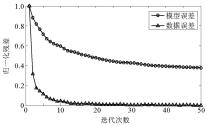
我们采用文中提出的弹性波最小二乘逆时偏移方法对该多分量炮集进行成像。图7为复杂天然气水合物模型的偏移参数。图8为不使用编码函数得到的弹性波最小二乘逆时偏移50次迭代的成像结果, 从图中我们可以明显的看到由于多炮混叠导致的串扰噪声。图9为使用编码函数得到的弹性波最小二乘逆时偏移50次迭代的成像结果。为了更好地对结果进行展示, 我们对成像结果进行了Laplacian滤波, 从图中可以得到与前面三层模型例子相类似的结果, 该方法得到了高分辨率和信噪比的成像结果, 由于多炮混叠导致的串扰噪声也通过编码函数的应用得到了很好的压制, v_s分量的成像结果比v_p分量具有更好的分辨率。模型中央, 天然气水合物储层得到了很好的成像, 成像结果能够很好地反应复杂的地下构造情况, 断层的断点位置也得到了很好的归位。为了进一步进行比较, 我们从图6、8、9中抽取了位于水平位置3.36 km的垂直曲线如图10所示, 图中黑色实线为真实的反射系数曲线, 蓝色虚线为本文方法得到的曲线, 红色曲线为未编码方法得到的曲线, 从图中的对比我们可以得到成像的振幅信息得到了很好的保真。从残差收敛曲线(图11)上可以看出:无论模型残差还是数据残差, 残差都迅速减少, 并得到了很好的收敛。最后通过该模型的试算, 我们可以得出:文中提出的弹性波最小二乘逆时偏移方法对于复杂的天然气水合物模型具有很好的适应性, 相比于传统的多分量弹性波逆时偏移其成像精度更高, 能够很好的应用到含天然气水合物实际工区的多分量地震成像中。

	Figure Option View Download New Window
	图7 复杂天然气水合物模型的偏移参数

	Figure Option View Download New Window
	图8 不使用编码函数得到的弹性波最小二乘逆时偏移成像结果a— v_p分量; b— v_s分量

	Figure Option View Download New Window
	图9 使用编码函数得到的弹性波最小二乘逆时偏移成像结果a— v_p分量; b— v_s分量

	Figure Option View Download New Window
	图10 在水平位置3.36 km处抽取的垂向反射系数a— v_p分量; b— v_s分量

	Figure Option View Download New Window
	图11 归一化残差曲线

3 结论与认识

1)文中提出了一种弹性波最小二乘逆时偏移方法, 并将该方法应用于天然气水合物储层多分量地震数据的高精度成像中, 得到了非常好的效果:相比于常规多分量弹性波逆时偏移方法, 本文方法压制了低频噪声和采集脚印噪声, 提高了信噪比和分辨率, 深部能量得到了一定的补偿, 能量更加均衡, 振幅的保真性高。同时将多炮数据组成一个超道集进行偏移, 将计算量水平减少到单炮水平, 并采用编码技术对多炮之间的串扰噪声进行了很好的压制;

2)文中提出的弹性波最小二乘逆时偏移方法能够得到更精确、分辨率更高的偏移成像, 有助于查明天然气水合物储层的精细结构。为弹性波最小二乘逆时偏移技术应用于天然气水合物实际资料提供了坚实的理论基础。

附件A:弹性波多参数最小二乘逆时偏移梯度公式求取基于伯恩近似理论, 参数的扰动

$\begin{matrix} δV (λ, μ, ρ) = V (λ, μ, ρ) - V_{0} (λ, μ, ρ) (A - 1) \end{matrix}$

可以引起波场的扰动:

$\begin{matrix} δU (x, t) = U (x, t) - U_{0} (x, t) (A - 2) \end{matrix}$

其中:U₀和V₀表示背景波场和背景参数, δ U和δ V为扰动波场和扰动参数。U=(v_x, v_z, τ _xx, τ _zz, τ _xz), V=(λ , μ , v_p, v_s, ρ ), 则可以求得背景波场U₀:

$\begin{matrix} \{\begin{matrix} ρ_{0} \frac{\partial v_{x 0}}{\partial t} = \frac{\partial τ_{xx 0}}{\partial x} + \frac{\partial τ_{xz 0}}{\partial z}, ρ_{0} \frac{\partial v_{z 0}}{\partial t} = \frac{\partial τ_{xz 0}}{\partial x} + \frac{\partial τ_{zz 0}}{\partial z}, \\ \frac{\partial τ_{xx 0}}{\partial t} = (λ_{0} + 2 μ_{0}) \frac{\partial v_{x 0}}{\partial x} + λ_{0} \frac{\partial v_{z 0}}{\partial z} + f_{x}, \\ \frac{\partial τ_{zz 0}}{\partial t} = (λ_{0} + 2 μ_{0}) \frac{\partial v_{z 0}}{\partial z} + λ_{0} \frac{\partial v_{x 0}}{\partial x} + f_{z}, \\ \frac{\partial τ_{zz 0}}{\partial t} = μ_{0} (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) 。 \end{matrix} (A - 3) \end{matrix}$

将U(x, t)=U₀(x, t)+δ U(x, t)代入方程(7)中, 然后减去方程(A-3)可得:

$\begin{matrix} \{\begin{matrix} ρ \frac{\partial δ v_{x}}{\partial t} = \frac{\partial δ τ_{xx}}{\partial x} + \frac{\partial δ τ_{xz}}{\partial z} - δρ \frac{\partial v_{x 0}}{\partial t} + O (δ ρ^{2}), \\ ρ \frac{\partial δ v_{z}}{\partial t} = \frac{\partial δ τ_{xz}}{\partial x} + \frac{\partial δ τ_{zz}}{\partial z} - δρ \frac{\partial v_{z 0}}{\partial t} + O (δ ρ^{2}), \\ \frac{\partial δ τ_{xx}}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{x}}{\partial x} + λ \frac{\partial δ v_{z}}{\partial z} + δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{x 0}}{\partial x} + O (δ λ^{2}) + O (δ μ^{2}), \\ \frac{\partial δ τ_{zz}}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{z}}{\partial z} + λ \frac{\partial δ v_{x}}{\partial x} + δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{z 0}}{\partial z} + O (δ λ^{2}) + O (δ μ^{2}), \\ \frac{\partial δ τ_{zz}}{\partial t} = μ (\frac{\partial δ v_{x}}{\partial z} + \frac{\partial δ v_{z}}{\partial x}) + δμ (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) + O (δ μ^{2}) 。 \end{matrix} (A - 4) \end{matrix}$

其中O(δ V²)表示δ V的高阶项。我们定义参数扰动的反射系数模型为:

$\begin{matrix} \{\begin{matrix} m (λ) = λ - λ_{0} \\ m (μ) = μ - μ_{0} \\ m (ρ) = ρ - ρ_{0} \end{matrix} (A - 5) \end{matrix}$

将方程(A-5)代入到方程(A-4)并忽略高阶项可得:

$\begin{matrix} \{\begin{matrix} ρ \frac{\partial δ v_{x}}{\partial t} = \frac{\partial δ τ_{xx}}{\partial x} + \frac{\partial δ τ_{xz}}{\partial z} - m (ρ) \frac{\partial v_{x 0}}{\partial t}, \\ ρ \frac{\partial δ v_{z}}{\partial t} = \frac{\partial δ τ_{xz}}{\partial x} + \frac{\partial δ τ_{zz}}{\partial z} - m (ρ) \frac{\partial v_{z 0}}{\partial t}, \\ \frac{\partial δ τ_{xx}}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{x}}{\partial x} + λ \frac{\partial δ v_{z}}{\partial z} + m (λ) (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 m (μ) \frac{\partial v_{x 0}}{\partial x}, \\ \frac{\partial δ τ_{zz}}{\partial t} = (λ + 2 μ) \frac{\partial δ v_{z}}{\partial z} + λ \frac{\partial δ v_{x}}{\partial x} + m (λ) (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 m (μ) \frac{\partial v_{z 0}}{\partial z}, \\ \frac{\partial δ τ_{zz}}{\partial t} = μ (\frac{\partial δ v_{x}}{\partial z} + \frac{\partial δ v_{z}}{\partial x}) + m (μ) (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) 。 \end{matrix} (A - 6) \end{matrix}$

所以方程(1)可以改写为

$\begin{matrix} \begin{matrix} E (λ, μ, ρ) = {(\begin{matrix} - δρ \frac{\partial v_{x 0}}{\partial t} \\ - δρ \frac{\partial v_{z 0}}{\partial t} \\ δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{x 0}}{\partial x} \\ δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{z 0}}{\partial z} \\ δμ (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) \end{matrix})}^{T} (\begin{matrix} v_{x}^{R} \\ v_{z}^{R} \\ τ_{xx}^{R} \\ τ_{zz}^{R} \\ τ_{xz}^{R} \end{matrix}) = \\ - δρ \frac{\partial v_{x 0}}{\partial t} v_{x}^{R} - δρ \frac{\partial v_{z 0}}{\partial t} v_{z}^{R} + [δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{x 0}}{\partial x}] τ_{xx}^{R} + \\ [δλ (\frac{\partial v_{x 0}}{\partial x} + \frac{\partial v_{z 0}}{\partial z}) + 2 δμ \frac{\partial v_{z 0}}{\partial z}] τ_{zz}^{R} + δμ (\frac{\partial v_{x 0}}{\partial z} + \frac{\partial v_{z 0}}{\partial x}) τ_{xz}^{R} \end{matrix} (A - 7) \end{matrix}$

对目标方程(1)求导, 我们可得到不同参数的梯度方程:

$g_{ρ} = \frac{\partial E}{\partial ρ} = \int (- \frac{\partial v_{x 0}}{\partial t} v_{x}^{R} - \frac{\partial v_{z 0}}{\partial t} v_{z}^{R}) dt 。 (A - 10)$

(本文编辑:叶佩)

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zanoth S R, Saenger E H, Krüger O S, et al. Leaky mode: A mechanism of horizontal seismic attenuation in a gas-hydrate-bearing sediment[J]. Geophysics, 2007, 72(5): E159-E163. [本文引用:1]
[2]	Stoll R D, Bryan G M. Physical properties of sediments containing gas hydrates[J]. J. Geophys. Res. , 1979, 84: 1629-1634. [本文引用:1]
[3]	Sloan E D. Clathrate hydrates of natural gases[M]. Marcel Dekker, 1990. [本文引用:1]
[4]	Kvenvolden K A. Aprimer on gas hydrates. U. S. Geological Survey[J]. Professional Paper 1570, 1993: 555-561. [本文引用:1]
[5]	Holbrook W S, Hoskins H, Wood W T, et al. Methane hydrate and free gas on the Blake Ridge from vertical seismic profling[J]. Science, 1996, 273: 1840-1843. [本文引用:1]
[6]	Guerin G, Goldberg D. Sonic waveform attenuation in gas hydrate-bearing sediments from the Mallik 2L-38 research well, Mackenzie Delta, Canada[J]. Journal of Geophysical Research, 2002, 107: 1029-1085. [本文引用:1]
[7]	Stoll R D, Bryan G M. Physical properties of sediments containing gas hydrates[J]. J. Geophys. Res. , 1979, 84: 1629-1634. [本文引用:1]
[8]	Bangs N L B, Sawyer D S, Golvovchenko X. Free gas at the base of the gas hydrate zone in the vicinity of the Chile triple junction[J]. Geology, 1993, 21: 905-908. [本文引用:1]
[9]	Hyndman R D, Spence G D. A seismic study of methane hydrate marine bottom simulating reflectors[J]. J. Geophys. Res. , 1992, 97: 6683-6698. [本文引用:1]
[10]	徐明才, 刘建勋, 柴铭涛, 等. 青海省天峻县木里地区天然气水合物地震响应特征[J]. 地质通报, 2011, 30(12): 1910-1917. [本文引用:1]
[11]	徐明才, 刘建勋, 柴铭涛, 等. 青海木里地区天然气水合物反射地震试验研究[J]. 地质与勘探, 2012, 48(6): 1180-1187. [本文引用:1]
[12]	Akihisa K, Tezuka K, Senoh O, et al. Well log evaluation of gas hydrate saturation in the miti nankai-trough well, offshore south east Japan[J]. SPWLA 43^rd annual logging symposium, 2002. [本文引用:1]
[13]	Claerbout J. Earth soundings analysis: Processing versus Inversion[J]. Black-well Scientific, 1992. [本文引用:1]
[14]	Nemeth T, Wu C, Schuster G. Least-squares migration of incomplete reflection data[J]. Geophysics, 1999, 64(1): 208-221. [本文引用:1]
[15]	Kuehl H, Sacchi M. Least-squares split-step migration using the Hartley transform[C]//Expand ed Abstracts of the 69^th Annual SEG Meeting. Society of Exploration Geophysicists, 1999: 1548-1551. [本文引用:1]
[16]	LeBras R, Clayton R. An iterative inversion of back-scattered acoustic waves[J]. Geophysics, 1988, 53(4): 501-508. [本文引用:1]
[17]	杨其强, 张叔伦. 最小二乘傅立叶有限差分偏移[J]. 地球物理学进展, 2008, 23(2): 433-437. [本文引用:1]
[18]	罗国安, 武威, 李合群, 等. 快速叠后偏移反褶积算法及应用[J]. 石油地球物理勘探, 2010, 45(6): 844-849. [本文引用:1]
[19]	黄建平, 李振春, 孔雪, 等. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J]. 地球物理学报, 2013, 56(5): 1-9. [本文引用:1]
[20]	黄建平, 曹晓莉, 李振春, 等. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 2014, (1): 107-112. [本文引用:1]
[21]	刘玉金, 李振春. 扩展成像条件下的最小二乘逆时偏移[J]. 地球物理学报, 2015, 10: 3771-3782. [本文引用:1]
[22]	郭书娟, 马方正, 段心标, 等. 最小二乘逆时偏移成像方法的实现与应用研究[J]. 石油物探, 2015, (3): 301-308. [本文引用:1]
[23]	曲英铭, 黄建平, 李振春, 等. 分层映射法起伏自由地表弹性波正演模拟与波场分离[J]. 石油地球物理勘探, 2016, (2): 261-271. [本文引用:1]
[24]	Qu Y, Huang J, Li Z, et al. A hybrid grid method in an auxiliary coordinate system for irregular fluid-solid interface modeling[J]. Geophysical Journal International, 2017, 208(3): 1540-1556. [本文引用:1]
[25]	Qu Y, Li Z, Huang J, et al. Elastic full-waveform inversion for surface topography[J]. Geophysics, 2017, 82(5): R269-R285. [本文引用:1]
[26]	曲英铭, 黄建平, 李振春, 等. 分层坐标变换法起伏自由地表弹性波叠前逆时偏移[J]. 地球物理学报, 2015, (8): 2896-2911. [本文引用:1]
[27]	Dai W, Fowler P, Schuster G. Multi-source least-squares reverse time migration[J]. Geophysical Prospecting, 2012, 60(4): 681-695. [本文引用:1]
[28]	Plessix R E, Mulder W A. Frequency-domain finite-difference amplitude- preserving migration[J]. Geophysical Journal International, 2004, 157(3): 975-987. [本文引用:1]
[29]	Plessix R. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. [本文引用:1]
[30]	Köhn D, De Nil D, Kurzmann A, et al. On the influence of model parametrization in elastic full waveform tomography[J]. Geophysical Journal International, 2012, 191: 325-345. [本文引用:1]
[31]	Qu Y, Li Z, Huang J, et al. Viscoacoustic anisotropic full waveform inversion[J]. Journal of Applied Geophysics, 2017, 136: 484-497. [本文引用:1]
[32]	Qu Y, Li Z, Huang J, et al. Multi-scale full waveform inversion for areas with irregular surface topography in an auxiliary coordinate system[J]. Exploration Geophysics, 2016. [本文引用:1]
[33]	Qu Y, Li Z, Huang J, et al. Irregular surface FWI in an auxiliary coordinate system based on the first-order velocity-stress equation[C]//Expand ed Abstracts of the 86^th Annual SEG Meeting. Society of Exploration Geophysicists, 2016: 1079-1083. [本文引用:1]
[34]	Liu Y, Symes W W, SLi Z. Multisource least-squares extended reverse-time migration with preconditioning guided gradient method[J]. SEG Technical Program, Expand ed Abstracts, 2013: 3709-3715. [本文引用:1]

2007

0.0

... ,分布于多年的冻土区沉积物或者高孔隙流体压力和低温条件下的深海沉积物中^[1],是由水和天然气在低温高压条件下形成的冰状固体物质^[2,3] ...

1979

0.0

... ,分布于多年的冻土区沉积物或者高孔隙流体压力和低温条件下的深海沉积物中^[1],是由水和天然气在低温高压条件下形成的冰状固体物质^[2,3] ...

1990

0.0

... ,分布于多年的冻土区沉积物或者高孔隙流体压力和低温条件下的深海沉积物中^[1],是由水和天然气在低温高压条件下形成的冰状固体物质^[2,3] ...

1993

0.0

... 10⁵万亿ft³的甲烷储藏于天然气水合物中^[4],与其他化石燃料的储量相当^[5] ...

1996

0.0

... 10⁵万亿ft³的甲烷储藏于天然气水合物中^[4],与其他化石燃料的储量相当^[5] ...

2002

0.0

... ②天然气水合物中甲烷含量超过80%,因此天然气水合物污染小^[6] ...

1979

0.0

... 对天然气水合物物性的研究主要可以分成实验室测量^[7]、直接提取岩心^[8]及地震反射特征研究^[9] ...

1993

0.0

... 对天然气水合物物性的研究主要可以分成实验室测量^[7]、直接提取岩心^[8]及地震反射特征研究^[9] ...

1992

0.0

... 对天然气水合物物性的研究主要可以分成实验室测量^[7]、直接提取岩心^[8]及地震反射特征研究^[9] ...

2011

0.0

徐明才, 刘建勋, 柴铭涛, 等. 青海省天峻县木里地区天然气水合物地震响应特征[J]. 地质通报, 2011, 30(12): 1910-1917.

天然气水合物是一种新型的潜在能源,广泛分布于大陆边缘海底沉积物和陆上永久冻土带中。2008年,在祁连山冻土区首次钻获天然气水合物实物样品。2010年,在木里地区开展了反射地震方法探测天然气水合物的试验研究,通过综合分析解释反射地震资料和地质资料,初步认为含天然气水合物介质形成的反射波在地震剖面上具有低速、弱振幅、高频的特征。在成藏机制上,天然气水合物的分布与深部断裂破碎带有关,天然气沿深部断裂构造向上运移,并受冻土层的封闭而富集,在合适的温压条件下形成天然气水合物矿藏。

... 徐明才等指出冻土区破碎带中含天然气水合物的地层具有较低的纵横波速度、密度及泊松比^[10,11] ...

2012

0.0

徐明才, 刘建勋, 柴铭涛, 等. 青海木里地区天然气水合物反射地震试验研究[J]. 地质与勘探, 2012, 48(6): 1180-1187.

天然气水合物是一种新型潜在能源,广泛分布于大陆边缘海底沉积物和陆上永久冻土带中。2008年,在我国祁连山冻土区首次钻获天然气水合物实物样品。2010年,作者在木里地区开展了反射地震方法探测天然气水合物的试验研究,通过综合分析解释反射地震和测井及地质资料,初步认为含天然气水合物介质形成的反射波在地震剖面上具有低速、弱振幅、高频的特征。在成藏机制上,天然气水合物的分布与深部断裂破碎带有关,天然气沿深部断裂构造向上运移,并受冻土层的封闭而富集,在合适的温压条件下形成天然气水合物矿藏。

... 徐明才等指出冻土区破碎带中含天然气水合物的地层具有较低的纵横波速度、密度及泊松比^[10,11] ...

2002

0.0

... Akihisa等对天然气水合物的物理参数特性进行了概括总结^[12] ...

1992

0.0

... 传统偏移方法大多数都是采用正演算子的共轭来代替它本身的逆^[13,14],也就是说,传统偏移方法可以准确地处理运动学信息,但是成像剖面的振幅无法准确地反映反射系数,这将会导致一系列成像问题,例如低频噪声、低信噪比、成像振幅不均衡及采集脚印等^[15] ...

1999

0.0

1999

0.0

1988

0.0

... 最小二乘偏移方法是一种线性反演方法,该方法可以提高成像剖面的分辨率并压制偏移噪声,可以得到真振幅剖面^[16] ...

2008

0.0

杨其强, 张叔伦. 最小二乘傅立叶有限差分偏移[J]. 地球物理学进展, 2008, 23(2): 433-437.

Conventional migration algorithms utilize the inversion of a forward modeling operator by analytical means. Alternatively, least-squares migration method involves a numerical approach where the solution is retrieved by solving a linear discrete inverse problem. In this case, we intend to seek a model that fits the seismic data and exhibits some certain features. Least-squares migration reduces migration artifacts and generally produces very accurate seismic images. Kirchhoff operator is popularly used in the least-squares migration. However, many iterations are required and the methods have the drawbacks belong to the Kirchoff migration method. In this paper, we apply the least-squares technique to the wave equation migration methods based on wave extrapolation. An key to improve the efficiency of lease-squares migration is adopting efficient modeling and migrations operator. We perform least-squares migration using efficient Fourier finite -difference modeling and migration operators. Numerical examples show that the least- squares images can be efficiently retrieved in a few iterations of conjugate gradients method. In addition, we adopt the numerical software FFTW to perform Fourier transformation, which generally is more than six times quicker than conventional FFT programs, therefore the algorithm become more efficient. The algorithm can be easily implemented in parallel architecture. These features make the algorithm very attractive.

一般偏移算法是用反演算子通过解析方法求解.最小二乘偏移方法采用另一种思路，即采用数值方法，通过解一个线性离散反问题来索求解.这样我们试着寻找一个模型匹配地震数据并能表现出其某些特点来得到偏移图像.最小二乘法能减少偏移赝像，得到更精确的偏移效果.Kirchhoff算子在最小二乘偏移方法中应用较广，但需要较多的迭代次数，而且具有Kirchhoff偏移的缺点.本文把最小二乘方法运用到基于波长延拓的波动方程偏移方法中，为提高最小二乘偏移的效率，可采用效率较高的正传播算子和反传播算子.我们利用效率较高，能适应剧烈横向变速的傅立叶有限差分正传播和反传播算子来做叠后最小二乘偏移.数值实例表明，通过少数的共轭梯度法迭代，就能得到与真实模型差别很微小的偏移效果.对于傅式变换我们采用了数值软件FFTW，其变换速度比常规FFT算法一般要快六倍以上，进一步提高了效率.本文算法很容易在并行机上实现，这些特点在处理大型数据时大有裨益.

... 2008年,杨其强等实现了基于傅里叶有限差分偏移算子的叠后最小二乘偏移,很好地克服了传统偏移方法的缺点,获得了高分辨率的成像剖面^[17] ...

2010

0.0

罗国安, 武威, 李合群, 等. 快速叠后偏移反褶积算法及应用[J]. 石油地球物理勘探, 2010, 45(6): 844-849.

偏移反褶积方法是一种提高偏移剖面分辨率的有效方法，求取偏移反褶积所需的格林函数基于采集观测系统以及速度模型只随深度变化的假设，但求取偏移反褶积滤波因子的计算量巨大，对于三维数据更是如此。本文提出基于均匀介质假设的叠后偏移格林函数的快速算法，其思路是：对于叠后数据来说，震源点与检波点是重合的，同时，可以认为其观测系统是规则的，再根据偏移格林函数平移不变性的假设，在每个深度上只需计算一个偏移格林函数即可。通过快速偏移反褶积方法，采用常速扫描来设计优化的偏移反褶积算子以处理横向变速情况。针对不同数据的初步实验表明，快速偏移反褶积算子能有效地提高计算效率和偏移剖面的成像质量。

... 2010年,罗国安等实现了一种快速的叠前最小二乘偏移算法,该算法是基于均匀介质假设下提出的,因此虽能在一定程度上改善成像质量,但在复杂介质上存在一定的问题^[18] ...

2013

0.0

黄建平, 李振春, 孔雪, 等. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究[J]. 地球物理学报, 2013, 56(5): 1-9.

... 2013年,黄建平将最小二乘逆时偏移(LSRTM)算法应用到碳酸盐岩成像方法中,但并没有应用于天然气水合物的成像中^[19] ...

2014

0.0

黄建平, 曹晓莉, 李振春, 等. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 2014, (1): 107-112.

... 2014年,黄建平等对近地表复杂构造进行了成像研究,同时还指出了最小二乘逆时偏移在近地表成像方面所具有的独特优势^[20] ...

2015

0.0

刘玉金, 李振春. 扩展成像条件下的最小二乘逆时偏移[J]. 地球物理学报, 2015, 10: 3771-3782.

摘　要：逆时偏移（RTM）是复杂介质条件下地震成像的重要手段.因受观测系统限制、上覆地层影响以及波场带宽有限等因素的影响,现行的常规RTM所采用的互相关成像条件通常对地下构造进行模糊成像.最小二乘逆时偏移（LSRTM）通过最小化线性Born近似正演数据和采集数据之间的波形差异,采用梯度类反演算法优化反射系数模型,获得的成像结果具有更高的分辨率和更可靠的振幅保真度.然而,基于波形拟合的LSRTM对背景速度模型的依赖性很强.误差太大的速度模型容易产生周波跳跃现象,导致LSRTM难以获得全局最优解.为了克服这一问题,本文基于扩展模型的思想,在线性Born近似下,推导得到RTM扩展成像条件.并基于最小二乘反演理论,提出扩展成像条件下的LSRTM方法.理论模型试算表明,本文方法不仅可以提供分辨率更高、振幅属性更为可靠的成像结果,而且能够在一定程度上消除速度误差对反演成像的影响.

... 2015年,刘玉金和李振春基于最小二乘理论和算法提出了一种扩展成像条件下的成像方法,能够在初始速度模型存在一定误差的情况下获取真振幅的LSRTM成像结果^[21] ...

2015

0.0

郭书娟, 马方正, 段心标, 等. 最小二乘逆时偏移成像方法的实现与应用研究[J]. 石油物探, 2015, (3): 301-308.

摘　要：复杂岩性油气藏勘探开发需要高保真的地震成像资料。与常规偏移方法相比,最小二乘逆时偏移（LSRTM）成像基于反演理论,可为岩性储层估计提供更加保真的高分辨率反射系数成像剖面,成为当前成像方法的研究热点和发展趋势。通过对误差泛函建立、逆时反偏移数据重构算法、Hessian逆预条件梯度计算及基于高斯-牛顿法的反演迭代更新方法等关键技术研究,实现了迭代最小二乘逆时偏移成像。为了使该偏移成像方法能够应用于实际资料,研究了针对性的数据预处理技术和最小平方匹配滤波模拟数据校正处理技术,探索建立了面向实际资料的最小二乘逆时偏移实现流程。某探区实际二维地震资料的最小二乘逆时偏移成像结果表明,相比传统的逆时偏移成像技术,最小二乘逆时偏移在成像分辨率和保幅性方面具有一定的优势。

... 同年,郭书娟将LSRTM理论应用到实际资料中,建立了LSRTM成像流程^[22] ...

2016

0.0

曲英铭, 黄建平, 李振春, 等. 分层映射法起伏自由地表弹性波正演模拟与波场分离[J]. 石油地球物理勘探, 2016, (2): 261-271.

Conventional finite difference method has some difficulties to deal with irregular free-surface. Conventional mapping method can overcome the disadvantage by transforming irregular surface to horizontal surface. But at the same time, the interface below the surface will be destroyed, resulting in inaccurate wave propagation and false reflection. Thus we improve the conventional mapping method and propose an elastic wave forward modeling and wave-field separation of irregular free-surface based on layered mapping method. After realizing the algorithm, several typical irregular free surface models are tested with the seismic forward modeling. The results suggest that:A. The layered mapping method can transform both the irregular surface and interface to horizontal surface and interface. Compared with conventional rectangular grids and conventional mapping method, the layered mapping method has a better adaptability for dual-complex structure; B. Forward modeling comparison tests prove that the layered mapping method has higher simulation accuracy and a better ability of suppressing dispersion; C. The wave-field separation of irregular free-surface based on layered mapping method can accurately separate P- and S-wave, which can provide a key approach for the irregular free-surface elastic imaging.

传统有限差分方法在处理起伏自由地表时存在一些问题;传统映射法通过将起伏地表映射为水平地表克服上述缺点,但在变换的同时会破坏原有地下构造,导致波传播的不准确和虚假反射的产生。为此,通过改进传统映射法,提出了分层映射法起伏自由地表弹性波正演模拟与波场分离方法,在实现算法的基础上,对几个典型起伏地表模型进行了正演模拟试算,结果表明:1分层映射法不仅可以将起伏地表映射为水平地表,而且也可以将地下起伏地层映射为水平地层。相对于传统矩形网格以及常规映射法,分层映射法对双复杂构造具有更好的适应性。2通过对比分层映射法、传统映射法、传统有限差分法的正演模拟试算结果表明,分层映射法具有更高的模拟精度和抑制频散能力。3基于分层映射法的起伏自由地表弹性波波场分离能够准确地将纵、横波分离,可为起伏自由地表弹性波偏移成像方法提供关键的技术支持。

... 前述的LSRTM方法是基于声波近似的单分量地震数据,没有利用多分量信息,而多分量地震勘探因其可以充分利用纵横波及转换波信息,所以可以对地下构造进行更准确的成像^[23,24,25],而弹性波成像方法能够充分利用多分量地震数据,因此近年来弹性波逆时偏移成像方法得到了推广应用^[26],但弹性波逆时偏移仍然存在如上文介绍的传统偏移方法的缺点,无法得到精确的成像 ...

2017

0.0

2017

0.0

2015

0.0

曲英铭, 黄建平, 李振春, 等. 分层坐标变换法起伏自由地表弹性波叠前逆时偏移[J]. 地球物理学报, 2015, (8): 2896-2911.

2012

0.0

... 在文中,我们使用预条件的共轭梯度法^[27]来解决最小二乘反问题 ...

2004

0.0

... 在文中,我们使用加权的保幅偏移方法作为预条件算子^[28] ...

2006

0.0

... 根据伴随状态理论^[29], 我们给出关于#cod#x003bb ...

2012

0.0

... 的梯度可由链式公式求得^[30]: ...

2017

0.0

... 编码多震源LSRTM通过将多炮叠加到一起组成一个或者若干个超道集,可以将弹性波最小二乘逆时偏移的计算量减少到与常规弹性波逆时偏移相当的水平,并通过编码函数来压制多炮数据的串扰噪声^[31,32,33] ...

2016

0.0

2016

0.0

2013

0.0

... 在文中,我们使用Liu等^[34]提出的单样本随机相移编码函数来压制不同炮记录之间的串扰噪声 ...