引用本文
俞岱, 孙渊, 路婧, 王颖, 边瑞峰. 层初至波旅行时层析并行算法及在地裂缝调查中的应用[J]. 物探与化探, 2017,41(5): 977-985.
YU Dai, SUN Yuan, LU Jing, WANG Ying, BIAN Rui-Feng. Parallel algorithm for shallow first-break traveltime tomography and its application in ground fissure investigation[J]. Geophysical and Geochemical Exploration, 2017,41(5): 977-985.
Doi:10.11720/wtyht.2017.5.28  
Permissions
Copyright©2017, 物探与化探编辑部
《物探与化探》编辑部
层初至波旅行时层析并行算法及在地裂缝调查中的应用
俞岱, 孙渊, 路婧, 王颖, 边瑞峰
长安大学 地质工程与测绘学院,陕西 西安 710054

作者简介: 俞岱(1986-),男,博士研究生,主要从事井中地震资料处理和逆时偏移工作。Email:tablemax47@126.com

收稿日期: 2017-07-03
基金: 中国地质调查局“汾渭盆地地面沉降地裂缝综合调查”子项目(12120115044901)
摘要

随着浅层地裂缝等地质灾害问题精细探测需求的增大,采用初至波速度层析反演技术,可以提供较高精度的浅层速度场的纵横向异常变化,可为识别地裂缝等地质灾害现象提供依据。通常,在采集参数一定的条件下,其反演成像精度受算法、网格类型和剖分尺度的限制,在网格类型不变的条件下,要提高精度就必须加密正反演计算网格,改进算法,从而实现增量而不减速且高精度的效果。文中利用OpenMP的单机多核并行技术,探讨并实现了初至波层析成像并行算法,其中正演部分使用了改进的旅行时线性插值法,针对原有的按列计算,加入了按行计算,充分考虑到来自各方向的射线,使得计算出的旅行时最小,反演部分使用了能迅速稳定收敛的LSQR法以及正则化技术,通过理论和实际资料测试,其收敛速度快,反演结果较好。同时,在加密采样和缩小网格尺度的条件下,与常规串行算法相比,其运算速度和效率有较大提高,与商业软件比较,其运算效率差异不大,但反演结果的精度和可分辨性较好。

关键词: 初至波层析; 正反演; OpenMP并行技术; 计算速度; 超线程技术; 地裂缝
中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2017)05-0977-09
Parallel algorithm for shallow first-break traveltime tomography and its application in ground fissure investigation
YU Dai, SUN Yuan, LU Jing, WANG Ying, BIAN Rui-Feng
College of Geology Engineering and Geomatics,Chang'an University,Xi'an 710054,China
Abstract

In the disaster geological problems such as shallow ground fissure etc. the demand for fine detection has been increasing in recent years. The first-break velocity tomography technique can provide a high accuracy of the vertical and horizontal anomalies of the shallow velocity field, and provide the basis for identifying the disaster geological phenomena such as ground fissures etc. In general, under certain conditions of acquisition parameters the accuracy of inversion imaging is limited by the algorithm, the grid type and the scale of the grid. Therefore, in order to improve the accuracy of the calculation and keep the grid type unchanged, the inversion of the grid need to be increased. On the basis of the improved algorithm, the effect of incremental and non-deceleration and high precision can be realized. In this paper, OpenMP-based stand-alone multi-core parallel technology is used, and the first-break tomography parallel algorithm is implemented. In the forward part, the improved traveltime linear interpolation method is used. The method of column calculation is used, and the method of line calculation is also used. In this case, the rays of each direction are taken into account, so that the minimum traveltime is obtained. In the inversion section, the LSQR method and the regularization technique are used. The results of theoretical and practical data test show that the convergence rate is fast and the inversion result is better. At the same time, compared with the conventional serial algorithm, the speed and efficiency of the algorithm are greatly improved under the condition of added sampling and reduced grid scale. Compared with commercial software,the change of computing efficiency is not obvious, but the accuracy and distinguishability of inversion results are better.

Keyword: first-break tomography; forward and inversion; OpenMP parallel technique; computational speed; hyper-threading; ground fissures
0 引言

层析成像法是20世纪70年代被引入地球物理学领域的, 经历了几十年的发展。20世纪80年代著名学者Anderson[1]、Daily[2]、Somerstein[3]、Bishop[4]等对该技术进行了大量的研究, 其基本原理已经十分成熟(尤其是地震走时层析成像), 而且在之后近十年的发展中, 其精度和分辨率都有很大的提高, 从二维发展到三维, 从各向同性发展到各向异性, 层析成像一直是地震勘探中一种十分重要的技术方法。地震走时层析成像是通过观测到的天然地震或人工地震走时利用模型重建算法反演地下介质结构、速度及其他弹性参数分布的一种反演方法。目前主要用于反演地下介质的速度分布和速度分界面的形态, 被广泛应用于地球内部结构探测、资源与能源勘探与开发、工程勘查与检测、地质灾害调查等领域。

地裂缝灾害是地质灾害中地面变形灾害的一种, 不仅造成各种建筑的直接破坏, 也引起了一系列的环境问题。现代地裂缝现象在世界许多国家都有发现, 其发生频率和灾害程度逐年加剧。自20世纪80年代后期, 物(化)探作为地裂缝研究的主要手段一直起着非常重要的作用 58, 这些方法中, 地震勘探因其勘探精度高、受地表物质干扰小、能够查明地下地裂缝展布关系, 而成为地裂缝勘探的首选。李忠生提供了西安地裂缝不同勘察阶段的地震勘探观测系统经验参数, 并给出依地震勘探结果开挖探槽的验证实例[9]。朱首峰分析了常规静校正在西安地裂缝浅层地震勘探资料处理中的不足, 并引入了煤田地震勘探中的非垂直静校正方法, 经过模型测试, 定量分析了非垂直静校正在资料处理中的有效性和必要性[10]。刘芳将折射地震层析成像应用于西安地裂缝勘探中, 通过多种反演算法比较, 证明LSQR算法具有反演速度快、稳定性好、反演精度高等优点, 反演得到的近地表地层速度场, 地裂缝位置处速度异常明显, 可成功探测出地裂缝[11]。彭建兵、孙渊针对西安黄土中地裂缝宽度小(一般仅数厘米)、深度10 m以下一般闭合、错断地层位移量较小等特点, 对西安地裂缝开展浅层地震精细探测工作, 了解了西安地裂缝发育及展布特征[12]。魏剑平通过高精度初至波和反射波联合速度反演对北京昌平某地地裂缝分布进行勘查, 取得了一定的成果[13]。刘智进行了汾渭盆地地裂缝浅层地震精细探测方法技术应用研究, 依据汾渭地区地裂缝的基本特征建立地裂缝的理论模型, 通过已有软件进行全波场正演模拟、反射波成像处理、初至波速度层析反演, 结合初至波层析结果和反射波成像结果分析认为, 一定尺度的裂缝与层析速度场异常变化和反射波场的变化特征有对应关系[14]。

文中针对浅层地裂缝地震精细探测方法技术中初至波速度层析成像算法精度及运算效率等展开分析, 重点就初至波正演计算中的算法改进和OpenMP单机多核层析并行算法等进行了探讨, 经地裂缝理论模型和实际资料测试, 在加密采样和缩小网格尺度的条件下, 与商业软件比较, 反演结果的精度和可分辨性较好。

1 方法原理
1.1 旅行时线性插值射线追踪法[13, 15, 16]

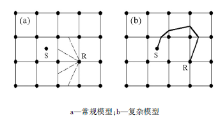
旅行时线性插值射线追踪法(linear traveltime interpolation, LTI)是由Asawaka于1993年提出的一种基于线性假设的网格单元扩展射线追踪方法, 其过程分为向前处理和向后处理。在向前处理中考虑来自各个方向的射线, 通过线性插值求出各个节点的旅行时, 在向后处理中从接收点开始利用费马原理对射线的传播路径进行追踪。传统的LTI算法存在问题是只考虑来自震源所在半平面的射线, 所以在向前处理中计算出的节点的旅行时可能不是最小旅行时, 这使得某些情况下正演得到的射线与走时不准确。如图1a所示, S点为震源点, R点为向后处理中的某一个交点, 传统LTI算法对R点最小地震波旅行时的计算只考虑了来自激发点所在左半平面的射线, 如图1b所示, 射线在异常复杂的速度结构当中存在这样的可能:即先绕到R点的右半平面再回折到S点。当出现射线回转的情况时, 用传统的LTI算法不能真正得到R点的最小地震波旅行时, 因而向后追踪得到的射线路径也无法满足费马原理。

图1 R点旅行时计算示意

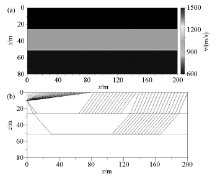
针对传统的LTI算法只考虑来自震源所在半平面的射线的问题, 改进方法是在向前处理过程中采用列循环和行循环相结合的方法来计算各单元边界节点的旅行时。下面通过模型试算来验证算法的改进效果, 这里先设置一个3层的模型(图2a), 第1层速度为600 m/s, 第2层速度为1 000 m/s, 第3层速度为1 500 m/s, 模型剖分网格大小为1 m× 1 m; 观测系统:震源位于(0, -10), 接收点位于(0, 0), (4, 0), …, (200, 0), 共51个接收点。传统LTI法追踪的射线路径如图2b。把模型旋转90° , 旋转后的模型如图3a所示, 相应的观测系统变为:震源位于(10, -200), 接收点位于(0, -200), (0, -196), …, (0, 0), 共51个接收点。对旋转后的模型用改进前、后两种射线追踪方法得到的射线路径如图3b、3c所示。对比图2b和图3b、3c中的射线路径和部分接收点旅行时(表1)可知, 旋转后模型用传统LTI法正演只能得到直达波, 这是没有考虑来自各个方向射线的结果, 旋转后模型用改进的LTI法计算得到的射线路径和旅行时与旋转前模型得到的是一致的, 改进后的LTI算法对复杂模型的适用性更强。

图2 传统LTI法正演模型(a)和射线追踪路径示意(b)

图3 改进后LTI法正演模型和射线追踪路径示意

表1 模型旋转前后部分接收点旅行时计算对比
1.2 旅行时层析反演[16, 17, 18]

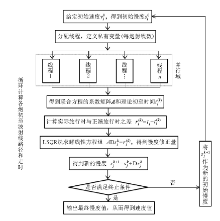
初至波旅行时层析反演, 首先是建立初始模型进行地震初至波走时正演, 此时需要将模型空间进行离散化, 假设每个网格单元内的慢度s为常数, 确定好观测系统之后可以计算每一个炮检对的初至波射线路径以及走时, 将计算的走时与实际观测到的走时做差, 残差为Δ T, 根据广义Radon变换, 假定慢度扰动很小, 慢度模型与扰动慢度模型中射线路径相同, 得到走时残差层析成像公式为AΔ s=Δ T, 其矩阵形式为:

a11a12…a1Na21a22…a2N⋮⋮⋮⋮aM1aM2…aMNΔs1Δs2⋮ΔsN=ΔT1ΔT2⋮ΔTM, (1)

其中:A是M× N维矩阵, 矩阵元素aMN代表第M条射线在第N个网格单元内的长度, Δ sN代表第N个网格单元的慢度扰动量, Δ TM代表第M条射线走时的残差。

传播矩阵A的构建是反演问题的关键, 笔者利用旅行时线性插值法正演可以得到初至波的传播矩阵以及初至波走时。式(1)通常是一个大型稀疏矩阵, 文中选择相对节省内存(利用大型稀疏矩阵的压缩存储技术)与计算量, 且能迅速稳定收敛的LSQR算法对方程进行求解。由于旅行时层析反演的不适定性, 层析问题的解通常含有某些不符合实际的高波数振荡, 因此文中在层析过程中加入正则化并对层析结果进行平滑, 这里正则化主要使用Laplace权值:

L=-1-1-1-18-1-1-1-1。(2)

选取Laplace权值即中心网格单元的值与周围8个网格的值的总和相等, 与层析反演中最小平方的思想结合, 就相当于在正则化作用的区域范围内慢度值不发生大的变化。

1.3 初至波旅行时层析反演并行算法实现

初至波旅行时层析反演的关键以及运算量最大的地方在传播矩阵的求取, 即正演计算。考虑到LTI法的原理以及层析反演中炮点数较多, 结合当下个人计算机已具备多线程与较大内存的特点, 选择利用OpenMP并行库对层析反演程序中正演部分的单炮循环进行并行化处理, 使得层析程序能更好的利用硬件资源, 更高效的完成计算。

图4为程序的流程图, 进行单炮LTI法正演时, 不需要其他炮点的信息, 据此将炮循环修改为OpenMP并行, 对个别正演使用到的变量进行私有属性定义, 即完成算法并行化改造。

图4 程序流程图

2 理论资料试算与并行效率评价
2.1 起伏地表层状断层模型试算

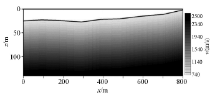
为了测试文中初至波旅行时层析反演程序的正确性, 建立一个起伏地表层状正断层模型进行测试, 模型如图5, 模型信息与观测系统详见表2。

图5 起伏地表层状正断层模型示意

表2 理论模型信息与观测系统信息

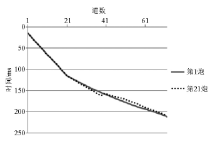
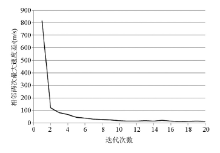
根据此模型和观测系统利用本文介绍的初至波旅行时线性插值法, 正演得到初至波走时, 作为初至波层析反演输入的观测走时。如图6所示为第1炮(坐标(4.00 m, -24.88 m))和第21炮(坐标(243.94 m, -25.67 m))初至波走时曲线对比、第21炮的初至波走时曲线在第37道附近有明显台阶, 这是由于该炮射线穿过断层导致的。建立如图7所示的反演初始速度模型, 模型横向与纵向的网格间距为2 m× 1 m, 从地表线起, 给初始速度740 m/s, 以纵向每5 m增加80 m/s的梯度依次递增直到 2 500 m/s为止。将以上的走时和速度模型作为输入, 利用本文层析反演程序, 得到如图9所示的反演结果, 图8为反演速度收敛曲线, 可见随着迭代次数的增加, 速度差依次递减, 迭代次数为20次时, 反演基本上收敛, 相邻两次的速度差仅为15 m/s。将理论模型的层位投到初至波层析反演的结果上, 第1层的速度分布与层位线对应性很好, 断层在第1层上的位置清晰可见, 第2层的反演结果次之, 断层在第2层上的位置较模糊, 但还可以区分出来, 第3层的速度结果以难区分断面位置, 通过射线分布图可知, 射线最深到达第3层界面附近, 浅层效果好于深层, 由于模型深层和左、右两侧射线较稀, 因此这些地方的反演结果稍差。为了测试加密采样对反演结果的影响, 在前述模型和观测系统基础上, 将道距加密到2 m, 以同样的初始模型又重新反演了一个结果, 如图10所示, 采样加密后的结果断面在浅层的刻画效果以及速度的成层性更好, 成像精度更高。总体而言, 本反演方法的效果较好, 达到了设计要求。

图6 单炮初至波走时曲线对比

图7 反演初始速度模型示意

图8 反演速度差收敛曲线

图9 理论模型初至波层析反演结果(道距4 m)与射线示意

图10 2 m道距层析反演结果

2.2 并行算法效率性评价

2.2.1 性能评价指标

并行算法的设计主要是为了加快程序的计算速率, 并有多个标准用于评判。通常用加速比和效率来评价并行算法的性能[19]。

1)加速比。多处理器下计算速度提升的倍数就是加速比, 即代码在单处理器下与多处理器下运算时间之比。计算公式为:

SP=T1/TP。(3)

式中:SP为加速比, T1是代码在单处理器下运算的时间, TP是指代码在多处理器下运算的时间。

2)效率。效率用于说明并行的效果。计算公式为:

EP=SP/P。(4)

式中:EP为效率, 一般小于1; SP为加速比; P为所使用的线程数。

2.2.2 并行效果分析

利用前述的理论模型资料, 在如表3所示的开发测试平台上进行本文介绍旅行时层析反演程序的并行算法效率评价。选择2 m× 1 m的网格间距, 所用线程数从1~4, 计算出各线程运行时间(为减小其他因素影响, 运算3次求均值)、并行加速比、并行效率, 详见表4。

表3 开发测试平台配置
表4 理论资料运算分析结果

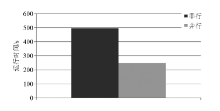
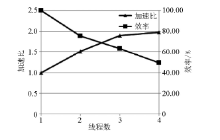
从表4中可见, 随着线程数的增加, 程序的运行时间减小, 将串行计算和4线程并行计算的运行时间进行比较, 如图11所示, 对道距4 m资料反演串行计算的运行时间为495.548 s, 而4线程并行计算的时间为249.771 s, 通过并行计算程序的运行时间大幅缩减, 加速比达1.98。如图12所示, 随着线程数的增加, 加速比增加, 效率减小, 加速比并不是按照线性递增, 由于效率随着线程的增加而减小, 导致加速效果有折扣, 整体上来说并行带来的速度提升明显。对比道距4 m时串行和道距2 m时4线程并行的计算时间, 在加密采样点数前提下, 通过并行技术达到了增量而不减速且高精度的效果。

图11 运行时间对比

图12 加速比和效率随线程数变化示意

2.2.3 对并行算法效率的影响

超线程技术, 简称HT(Hyper-Threading)技术, 由英特尔公司于2002年提出并研发[20], 现为主流化的技术, 它是利用特殊的硬件指令, 将一个处理器核模拟为两个逻辑内核[21], 让每个单独的处理器都能运用线程级并行计算, 从而减少CPU的闲置时间, 提高CPU的运行速度。英特尔公司表示, 采用超线程技术, 处理器仅增加5%的固件面积, 就可以换来15%到30%的效能提升[20]。在实际使用过程中, 超线程会在某些程度上降低效能, 因为它是两个线程共用单个处理器的资源, 因此当出现资源占用冲突时, 其中一个线程就要临时退出资源, 直到闲置后才能够继续使用[22]。因此, 超线程得出的线程性能并不等价于两颗CPU的性能。

本次测试平台为双核四线程的计算机, 其具有超线程技术。因此有必要测试超线程技术对于本文介绍的并行算法在效率方面的影响。本平台在关闭超线程技术后, 就变为双核二线程计算机, 因此并行运算时最多只进行2线程并行运算。利用前述的道距4 m的理论资料, 在测试平台关闭超线程技术之后对其进行串行和2线程并行运算, 计算出程序运行时间、并行加速比以及并行效率, 详见表5。对比可知:关闭超线程技术后, 2线程并行运算的加速比和效率均高于打开时2线程并行的值, 而略低于4线程并行运行的值, 将关闭超线程下2线程并行的值换算到4线程情况下, 加速比为1.8, 效率为45%, 性能基本与打开超线程下4线程并行时相当, 说明针对计算量大的并行程序时超线程技术优势并不明显, 而且从串行计算的运行时间来说, 关闭超线程技术时运算更快, 建议在运算量较大的工作站或服务器上可将超线程技术关闭, 因为其对提高并行运算效率帮助不大, 而且在关闭超线程技术时处理器进行串行计算可最大发挥运算性能, 毕竟算法程序不太可能做到完全并行计算, 其中会有一些串行计算存在。

表5 打开/关闭超线程技术情况下理论资料运算分析结果
3 实际资料测试

为了进一步验证本文层析反演的效果, 选取陕西某地实测地裂缝地震勘探资料对程序进行测试。该资料为查明可能存在的地下地裂缝分布以及构造的起伏变化。工区位于关中盆地, 区内浅表层大部分为黄土覆盖, 局部有基岩出露, 浅表层吸收衰减较大且地震地质条件良好。针对工区实际, 通过试验确定二维地震采集参数为:震源为炸药震源, 药量3 kg, 炮孔深度5 m; 激发方式为单边放炮, 测线长 1 305 m, 道距10 m, 变道数接收, 炮数22炮, 采样率0.5 ms, 记录长度为1.0 s。

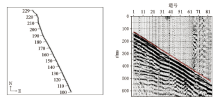
测线分布如图13中左图所示, 测线较直, 故可利用二维层析反演程序试算。通过对实际资料中初至波走时的拾取(如图13中右图所示), 使用本文的方法和Green Mountain层析软件进行初至波旅行时层析结果比较。图14左边为本文反演方法的速度收敛曲线, 可见其收敛性较好。图14右边为反演的初始模型示意图。

图13 工区测线平面图(左)与初至波旅行时拾取图(右)

图14 初至波旅行时反演速度收敛曲线(左)和反演初始模型示意(右)

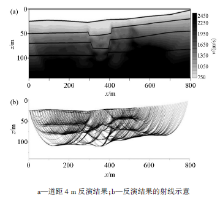
图15为Green Mountain软件的反演结果, 图16为本文方法得到的结果, 根据射线的分布将无射线部分切除, 对反演结果进行解释, 两种反演结果形态大体一致, 本文反演结果的射线分布更广, 有效范围更大, 速度分布成层性更好, 对地裂缝的可分辨性较好。通过初至波层析反演结果可以解释出地下地裂缝分布, 本方法的实际资料应用效果较好。

在本测试平台上将实际资料进行串行和并行(4线程并行)运算时间对比, 串行时间为259.133 s, 并行时间为129.453 s, 说明并行计算时运行时间大幅缩短, 在实际工作中可以有效地节省计算时间, 提高工作效率。

图15 Green Mountain初至波旅行时反演结果及其射线分布示意

图16 本文方法初至波旅行时反演结果及其射线分布示意

4 结论

本文介绍的初至波层析成像并行算法, 其中正演部分使用了改进的旅行时线性插值法, 针对原有的按列计算, 加入了按行计算, 充分考虑到来自各方向的射线, 使得计算出的旅行时最小, 反演部分使用了能迅速稳定收敛的LSQR法以及正则化技术。

本方法在地裂缝勘查工作中的应用效果较好, 与专业Green Mountain软件结果对比, 其射线分布更广, 有效范围更大, 速度分布成层性更好, 对地裂缝的可分辨性较好。

通过对测试资料进行并行效率分析可知, 并行算法可以有效的提高程序计算效率, 建议在运算量较大的工作站或服务器上可将超线程技术关闭, 因为其对提高并行运算效率帮助不大。

The authors have declared that no competing interests exist.

参考文献
[1] Anderson D L, Dziewonski A M. Seismic tomography[J]. Scientific American, 1987, 251(251): 60-68. [本文引用:1]
[2] Daily W D. Underground oil-shale retort monitoring using geotomography[J]. Geophysics, 1984, 49(10): 1701-1707. [本文引用:1]
[3] Somerstein S F, Berg M, Chang D, et al. Radio-frequency geotomography for remotely probing the interiors of operating mini- and commercial-sized oil-shale retorts[J]. Geophysics, 1984, 49(8): 1288-1300. [本文引用:1]
[4] Bishop T N, Bube K P, Cutler R T, et al. Tomographic determination of velocity and depth in laterally varying media[J]. Geophysics, 1985, 50(6): 903-923. [本文引用:1]
[5] 唐大荣, 雷炜, 彭成. Mini-Sosie浅层高分辨反射波技术在西安市地裂缝研究中应用[J]. 地球物理学报, 1988, 31(6): 708-712. [本文引用:1]
[6] 唐大荣. 一种浅层地震勘查新震源——震源弹应用效果[J]. 物探与化探, 1991, 15(2): 152-154. [本文引用:1]
[7] 肖宏跃, 雷宛. 用高密度电法探测西安地区地裂缝的应用效果[J]. 物探与化探, 1993, 17(2): 147-150. [本文引用:1]
[8] 韩许恒, 郁春霞. 氡射气测量在西安地裂缝勘察中的应用研究[J]. 工程地质学报, 1997, 51(1): 65-71. [本文引用:1]
[9] 李忠生. 西安地裂缝勘察中的地震勘探[J]. 工程勘察, 2004(5): 64-67. [本文引用:1]
[10] 朱首峰. 西安地裂缝与地面沉降调查地震勘探方法技术应用研究[D]. 西安: 长安大学, 2008. [本文引用:1]
[11] 刘芳. 折射波层析成像在西安地裂缝勘探中的应用研究[D]. 西安: 长安大学, 2009. [本文引用:1]
[12] 彭建兵著. 西安地裂缝灾害[M]. 北京: 科学出版社, 2012, 137-198. [本文引用:1]
[13] 魏剑平. 高精度初至波和反射波联合速度反演[D]. 西安: 长安大学, 2012. [本文引用:2]
[14] 刘智. 汾渭盆地地裂缝浅层地震精细探测方法技术应用研究[D]. 西安: 长安大学, 2013. [本文引用:1]
[15] Asakawa E, Kawanaka T. Seismic ray tracing using linear traveltime interpolation[J]. Geophysical prospecting, 1993, 41(1): 99-111. [本文引用:1]
[16] 叶佩. 地震初至波与反射波旅行时联合层析成像[D]. 西安: 长安大学, 2011. [本文引用:1]
[17] 张风雪, 余大新, 张广成. 地震射线走时层析成像的简单数值例子[J]. 地球物理学进展, 2014, 29(3): 1080-1083. [本文引用:1]
[18] 刘玉柱, 杨积忠. 有效利用初至信息的偏移距加权地震层析成像方法[J]. 石油物探, 2014, 53(1): 99-105, 115. [本文引用:1]
[19] 李祎昕. 地震勘探频率域二维正演并行算法研究[D]. 北京: 中国地质大学(北京), 2014. [本文引用:1]
[20] Marr D T, Binns F, Hill DL, et al. Hyper-threading technology architecture and microarchitecture[J]. Intel Technology Journal Q1, 2002. [本文引用:2]
[21] Borozan J. Microsoft windows-based servers and intel hyper-threading technology[J]. Microsoft Corporation, 2002, 15. [本文引用:1]
[22] 林杰, 余建坤. 比较分析CPU超线程技术与双核技术的异同[J]. 计算机应用与软件, 2011, 28(12): 293-294, 297. [本文引用:1]