引用本文
郭奇, 曾昭发, 于晨霞, 张思萌. 基于高精度字典学习算法的地震随机噪声压制[J]. 物探与化探, 2017,41(5): 907-913.
GUO Qi, ZENG Zhao-Fa, YU Chen-Xia, ZHANG Si-Meng. Seismic random noise suppression based on the high-precision dictionary learning algorithm[J]. Geophysical and Geochemical Exploration, 2017,41(5): 907-913.
Doi:10.11720/wtyht.2017.5.17  
Permissions
Copyright©2017, 物探与化探编辑部
《物探与化探》编辑部
基于高精度字典学习算法的地震随机噪声压制
郭奇1,2, 曾昭发1, 于晨霞1, 张思萌1
1.吉林大学 地球探测科学与技术学院,吉林 长春 130026
2.中水东北勘测设计研究有限责任公司,吉林 长春 130062

作者简介: 郭奇(1987-),男,硕士研究生,主要研究方向为地震数据处理方法。

收稿日期: 2016-08-26
摘要

地震勘探中的随机噪声会对有效信号产生严重干扰,甚至会导致信号畸变。为了满足高精度的地震勘探要求,应用高精度字典学习算法压制随机噪声。该算法基于超完备稀疏表示理论,对传统的字典学习算法从字典训练和稀疏编码两个方面进行了改善:在字典训练阶段,保持支集完备的情况下,对字典进行循环更新,使字典更好地适应数据;在稀疏编码阶段,选用上一轮更新的部分大系数作为新一轮迭代的初始系数,充分利用大系数表示有效信号的特点。对理论数据和实际含噪地震资料的处理结果表明,与传统算法相比,高精度字典学习算法在去噪的同时能保护有效信息,明显改善去噪精度,对地震记录信噪比的提高有显著优势。

关键词: 地震去噪; 字典学习; 稀疏表示; 随机噪声; 信噪比
中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2017)05-0907-07
Seismic random noise suppression based on the high-precision dictionary learning algorithm
GUO Qi1,2, ZENG Zhao-Fa1, YU Chen-Xia1, ZHANG Si-Meng1
1.College of Geo-Exploration Science and Technology,Jilin University,Changchun 130026,China
2.China Water Northeastern Investigation,Design & Research Co. Ltd.,Changchun 130062,China;
Abstract

In seismic exploration,the random noise severely distorts and interferes with seismic signals,and hence the denoising process is very important.In order to meet the high-precision requirement,the authors,based on the sparse and redundant representation theory,improve the dictionary update stage and the sparse coding stage in the conventional dictionary learning algorithm.While keeping the supports intact,the dictionary atoms are recurrently updated to adapt them to the specific seismic data.In the dictionary domain,large coefficients represent effective signals.Taking full advantage of this characteristic,the authors use several large coefficients from the last round of iteration as initial coefficients.In this way,the computational efficiency of the learning algorithm can be improved.The new algorithm is applied to synthetic and field seismic records and compared with the conventional K-SVD algorithm.The denoising results are satisfactory.It is shown that the new method can remove the random noise and protect the effective information at the same time.It is competitive in improving the signal-to-noise ratio of seismic records.

Keyword: seismic denoising; dictionary learning; sparse representation; random noise; signal-to-noise ratio
0 引言

随着油气需求的增加, 油气勘探逐步转向复杂的油气藏, 而复杂的地质环境中采集到的地震数据往往含有严重的噪声干扰, 有效地震信号能量较弱。因此, 如何有效地压制随机噪声、提高信噪比成为地震数据处理的挑战, 这也是进行后续地震资料解释、油气矿藏判断的重要基础。

稀疏表示理论突破了Nyquist采样定理[1]的限制, 大大降低了计算复杂度, 被广泛应用于信号处理领域。所谓信号的稀疏表示, 就是在变换域内用尽量少的变换系数来表示原始信号。目前, 基于稀疏表示理论的去噪方法已经被广泛用于地震数据去噪领域, 对地震数据进行某种变换, 在变换域内剔除低于设定阈值的系数, 以达到压制噪声的目的。小波变换[2, 3]、曲波(curvelet)变换[4, 5, 6]、剪切波(shearlet)变换[7, 8]等变换方法都曾被应用在地震数据噪声压制领域, 小波变换具有良好的局部时频分析能力, 可以有效地捕捉点奇异特征, 但对于曲线形状的地震波前则表达能力不足, 不可避免地会损失地震信号的细节信息; curvelet变换和shearlet变换都是多尺度多方向的变换方法, 在一定程度上弥补了小波变换的不足, 已被广泛应用于地震数据重构和噪声压制方面[9]。上述变换方法都是基于单一变换基函数的, 无法根据信号特征的变化进行调整, 对于准确地表达地震信号特征存在局限性, 常常会引入伪吉布斯效应[10]。因此, 学者们试图寻找一种方法, 能够自适应地根据地震数据自身的特点, 构造出适合于具体数据的变换基函数。Elad[11]等人首先提出了采用具有自适应学习能力的超完备冗余字典进行图像的稀疏分解, 基于数据驱动的超完备冗余字典通过对数据的不断学习和训练, 可以发展出更适应于目标数据的变换基函数, 从而能够更稀疏地表示目标数据。该方法一经提出, 在图像去噪和重构领域便得到了广泛应用, 并取得了令人满意的效果[12,13,14,15,16,17,18]。受此方法的启发, Tang G[19, 20]等人将这种自适应学习的字典应用到了地震数据去噪中, 离散余弦(DCT)字典作为初始字典, 经过学习和训练能够更稀疏地表示地震数据, 改善了单一变换基的去噪效果。2006年, Aharon等人提出K-SVD算法 [21,22,23], 该算法根据误差最小的原则, 对误差进行奇异值分解, 将误差最小时的分解值作为更新的字典原子, 提高了噪声压制效率。邵婕等人[24]将K-SVD字典训练算法与小波变换相结合, 在压制微地震资料中的随机噪声方面取得了良好的效果, 进一步验证了这种自适应学习思想的可行性。

在稀疏编码阶段常用的算法是贪婪追踪算法[25, 26], 主要是通过每次迭代求解局部最优解, 从而逐步实现对信号的逼近, 该类算法具有计算复杂度低、容易实现的优点, 且求解效果较好。正交匹配追踪算法(OMP)在正交方向上寻找非零系数, 提高了算法的收敛速度。Smith 等人[27]提出了高精度字典学习算法处理图像去噪, 对字典更新和稀疏编码这两个阶段分别进行了改进, 通过循环更新字典寻找更适应于特定图像的字典原子, 采用更高效地追踪算法进行稀疏编码, 在一定程度上提高了算法的收敛速度。笔者将这种改进后的字典学习算法应用到了地震随机噪声的压制过程中, 并与传统的K-SVD字典学习算法进行定量的对比, 显示出了高精度字典学习算法相对于传统KSVD字典学习算法在噪声压制方面的优势。

1 方法原理
1.1 超完备稀疏表示理论

假设含噪的地震模型可以表示成:

Y=X+ε, (1)

式中:Y∈ Rn× N表示待处理的含噪地震数据, 由列向量{yi }j=1N组成, X表示不含噪声的理想数据, ε 表示随机噪声, 噪声压制过程就是移除Y中的噪声, 尽可能准确地估计出X。给定一个集合D={dk, k=1, 2, 3, …, K}, 其中dk是张成Hilbert空间H∈ RN的单位矢量, 则信号yk可以用D中的若干个原子对其进行线性表示[21]:

式中:am为相应的展开系数, 较大的稀疏系数包含了有效信号的特征, 较小的稀疏系数则更多的代表噪声信号的特征。M表示稀疏度, 当M≪N时, 这种对信号的表示方式就称为稀疏表示; 当K≫N时, 集合D是一个超完备冗余字典, 式(2)所示的线性逼近则称为超完备稀疏表示。在这个超完备空间中, 信号的表示是非唯一的, 从稀疏表示的角度来说, 非零系数越少则说明对信号的表示越稀疏, 因此稀疏表示问题即为求非零元素个数的最小值[20]:

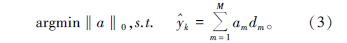
地震随机噪声压制是一个复杂的最优化问题, 可用下面含罚项函数表示[24]:

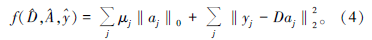
式中, A表示与信号矩阵Y对应的稀疏系数矩阵, aj∈ A; μ 是罚函数的权重, 用于控制稀疏程度。利用字典学习算法解决上述问题的关键在于寻找超完备冗余字典D和稀疏系数矩阵A。

1.2 基于K-SVD的字典循环更新算法(DUC)

在字典更新阶段, 原始数据作为字典更新的初始信号, 并假设稀疏系数矩阵A已知, 更新字典 D˙20:

D˙=argmin‖Y-DA‖F2, s.t.　A☉M=0=argmin‖Ej-djaTj‖F2, s.t.∀1≤j≤n, aj☉mj=0(5)

式中:A☉M是两个同尺寸矩阵的Schur积。M是一个由0和1组成的掩码矩阵, A☉M=0可以使所有的零项都保持完备。dj表示字典D中的第j列, aTj表示系数矩阵的第j行。采用块坐标下降法对字典每列原子进行优化, 这一过程通过对矩阵Ej= ☉(Id· mTj)进行奇异值分解来实现, mTj表示M的第j行, 促使aj中的零系数保持在合适的位置。掩码矩阵1d· mTj是通过d次复制 mTj得到的d× N的矩阵, 能够有效地从Y- di aTi中剔除没有用到第j列原子的样本列。

按j=1, 2, …, n的顺序更新完字典所有列即对字典进行了一次完整的更新, 但为了能更好地适应不同的地震数据特征, 对字典进行循环更新(DUC)[27]。需要指出的是, 在整个噪声压制的过程中, 计算效率主要受稀疏编码阶段的影响, 尽管字典循环过程会使算法变得复杂, 但总的去噪时间基本不会增加。

1.3 基于稀疏系数再利用的OMP算法(CoefROMP)

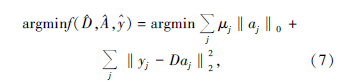
在稀疏编码阶段, 假设字典 D˙和信号 y˙都是已知的, 用优化算法求解字典域的稀疏表示系数A[20]:

对于超完备冗余字典, 式(7)中的ℓ0问题是一个NP问题, Chen等人将其转化为:

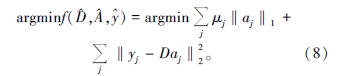
由于解的非唯一性, 很难求得精确的解, 但很多追踪算法可以获得有效的近似解, 如匹配追踪(MP)算法或正交匹配追踪(OMP)算法。传统的追踪算法都是将上一轮迭代得到的信号估计作为残差的初始值, 并没有充分发挥大系数的稀疏作用。Leslie N.Smith[27] 等人对OMP算法进行了改进, 提出了基于稀疏系数再利用的OMP算法— — CoefROMP(Coefficient Reuse OMP)算法。在每次迭代时, 从上一次更新得到的较大系数中选择一部分作为新一轮迭代的初始系数。CoefROMP算法在每次迭代时都要用到上一次迭代更新的部分系数, 所以只能在用常规追踪算法完成一次系数更新后才执行CoefROMP算法。经过多次数值试验我们发现, 选择前k/3(k表示非零元素的个数)个大系数作为初始系数会得到较好的稀疏表示结果。以第j列系数aj为例, 其更新的主要过程如下[27]:

1)输入: D˙, y˙j, aj, k;

2)初始化:从aj中选取前k/3个系数, T0:=sort(|aj|, k/3), r0:= y˙j- D˙T0ajT0, σ 0:=‖ r0‖ 2;

3)第n次迭代:取出投影后的残差中前k/3个系数Sn:=sort(| D˙Trn-1|, k/3);

合并支集 T˙n:= (Tn-1, Sn);

利用最小二乘法计算: a˙jn:= ( D˙T˙n)† rn;

从中取出k个或少于k个元素:Tn:=sort(| a˙jn|, k);

最小二乘法更新稀疏系数: a˙jn:= ( D˙Tn)+ y˙j;

更新残差:rn:= y˙j- D˙Tna˙jn, σ n:=‖ rn‖ 2;

如果σ n> σ n-1, 停止迭代;

4)输出:更新后的 a˙j。

2 数值模拟
2.1 理论模型

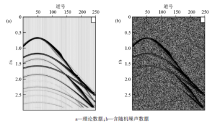
为了验证上述算法的去噪效果, 在传统的K-SVD算法的基础上, 笔者对合成的理论地震记录进行了处理, 该地震记录共250道, 每道750个采样点, 采样间隔4 ms。图1显示了合成地震记录、加入δ =30的高斯白噪声的地震记录。首先我们选DCT字典作为初始字典, 分别测试DUC算法和CoefROMP算法的性能。图2a为字典训练过程中均方根误差(RMSE)与迭代次数之间的关系。相比在每次迭代中仅更新一次字典, 更新两次或四次字典以少量的计算量为代价, 在一定程度上改善了训练结果。理论上来讲, 在每次迭代中更新字典循环次数越多, 得到的结果越理想, 但考虑到计算效率, 我们一般选择两次字典更新循环。图2b对比了CoefROMP算法和OMP算法的性能。与OMP算法相比, CoefROMP算法不但大大降低了稀疏编码的均方根误差, 也显著提高了算法的收敛速度, 正好弥补了字典循环更新带来的效率降低的不足, 所以用DUC算法和CoefROMP算法同时改善KSVD算法的字典学习阶段和稀疏编码阶段, 将会在不增加计算量的前提下提高地震数据去噪质量。

图1 合成地震记录

图2 RMSE与迭代次数的关系

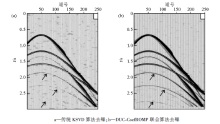
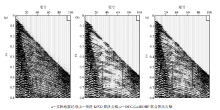
用DUC-CoefROMP联合算法对图1b中的含噪地震记录进行去噪处理, 并与传统的KSVD算法对比, 如图3所示。直观上来看, 两种方法都去除了大部分的随机噪声, 但用传统KSVD算法得到的去噪结果(图3a)中“ 背景斑块” 严重, 而用本文中的算法显著改善了这一现象(图3b), 结果与理论数据很逼近, 深部同相轴清晰。图4是两种方法去噪后得到的差剖面, 在传统KSVD算法去噪后的差剖面图(图4a)中可以明显地看到同相轴痕迹, 在去除噪声的同时, 也损失了大量的有效地震信号, 而用本文中的方法得到的差剖面(图4b)中几乎看不到有效地震信息, 说明该方法在去噪的同时保护了有效信号。

图3 不同方法去噪结果对比

图4 不同方法理论地震数据去噪差剖面对比

为了量化地进行对比, 定义峰值信噪比(RPSN):

RPSN=20lg‖s0‖2‖s1-s0‖211

其中, s1表示含噪地震数据, s0表示去噪后的地震数据。

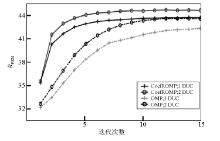
图5给出了应用4种算法的结果对比, 字典仅更新一次、稀疏编码算法为OMP算法即表示传统的KSVD算法。从图中可以看出, 在迭代次数相同和稀疏编码算法相同的情况下, 两次字典循环得到的去噪结果信噪比稍高于一次字典更新, 但计算量几乎不会减少; 在迭代次数相同和字典循环次数相同的情况下, 用CoefROMP算法得到的去噪结果信噪要显著高于OMP算法, 收敛速度加快, 这与图2结果也正好吻合。DUC-CoefROMP联合算法得到的去噪结果显著高于传统的KSVD算法, 计算量也明显减少。

图5 不同方法去噪性能对比

2.2 实际资料

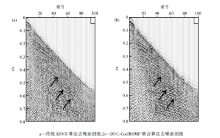
为了验证DUC-CoefROMP联合算法在实际生产中的应用效果, 对实际地震数据进行去噪处理。图6a是截取的某陆地二维地震记录, 记录中含有较强的随机噪声, 对有效信号, 尤其是深部的同相轴, 产生了严重的干扰。图6b和图6c是分别用传统KSVD算法和DUC-CoefROMP联合算法压制噪声的结果, 从黑框标出的部分可以看出, 传统的KSVD算法在压制噪声的同时也去掉了部分有效信号, 导致同相轴不够连续, 而DUC-CoefROMP联合算法压制了大部分随机噪声, 而且同相轴比前者更为清晰连续, 提高了去噪资料的保真度。图7a是传统的KSVD算法去噪差剖面, 除了随机噪声外, 在箭头处可以明显地看到部分同相轴信息; 图7b是DUC-CoefROMP联合算法去噪差剖面, 可见同相轴较少, 在压制随机噪声的同时保护了有效信号, 去噪效果显著。

图6 实际地震数据去噪结果

3 结论

高精度的字典学习算法对字典学习过程分别从字典训练和稀疏编码两个方面进行了简单有效的改进:字典训练阶段, 在保持支集完备的前提下, 循环更新字典以找到最优的原子; 在稀疏编码阶段, 利用上一次迭代的部分大稀疏系数进行新一轮的系数更新, 充分利用了大系数代表有效信号的特征。笔者应用这种高精度的字典学习算法处理了含有随机噪声的地震资料, 实验结果表明:

1) 字典更新循环次数越多, 字典原子越能适应

图7 实际地震数据去噪差剖面对比

信号特征, 但这要以较大的计算量为代价, 所以在选择字典更新次数时需要综合考虑字典训练效果和计算效率;

2) CoefROMP算法能在一定程度上提高字典训练效果, 且算法收敛速度快于OMP算法;

3) DUC-CoefROMP联合去噪在不增加计算量的情况下, 可以改善传统KSVD算法的去噪结果, 提高地震记录的信噪比和保真度。

The authors have declared that no competing interests exist.

参考文献
[1] 孙晶明. 压缩感知中观测矩阵的研究[D]. 武汉: 华中科技大学, 2013. [本文引用:1]
[2] Yu L L. EEG de-noising based on wavelet transformation[C]//Proceedings of the 3rd International Conference on—Bioinformatics and Biomedical Engineering. Beijing, China: IEEE, 2009: 1-4. [本文引用:1]
[3] 李雪英, 张晶, 孔祥琦, 等. 基于离散小波变换的地震资料自适应高频噪声压制[J]. 物探与化探, 2013, 37(1): 165-170. [本文引用:1]
[4] 何柯, 周丽萍, 于宝利, 等. 基于补偿阈值的曲波变换地面微地震弱信号检测方法[J]. 物探与化探, 2016, 40(1): 55-60. [本文引用:1]
[5] 刘国昌, 陈小宏, 郭志峰, 等. 基于Curvelet变换的缺失地震数据插值方法[J]. 石油地球物理勘探, 2011, 46(2): 237-246. [本文引用:1]
[6] 薛永安, 王勇, 李红彩, 等. 改进的曲波变换及全变差联合去噪技术[J]. 物探与化探, 2014, 38(1): 81-86. [本文引用:1]
[7] 刘成明, 王德利, 王通, 等. 基于Shearlet变换的地震随机噪声压制[J]. 石油学报, 2014, 35(4): 692-699. [本文引用:1]
[8] 王德营, 李振春, 董烈乾. Shearlet域和TT域联合压制面波方法[J]. 石油地球物理勘探, 2014, 49(1): 53-60. [本文引用:1]
[9] 路交通, 曹思远, 董建华, 等. 基于稀疏变换的地震数据重构方法[J]. 物探与化探, 2013, 37(1): 175-179. [本文引用:1]
[10] Kelly S E. Gibbs phenomenon for wavelets[J]. Applied and Computational Harmonic Analysis, 1996, 3(1): 72-81. [本文引用:1]
[11] Elad M, Aharon M. Image denoising via learned dictionaries and sparse representation[C]//Proceedings of IEEE Computer Society Conference on Computer Vision & Pattern Recognition. New York, NY, USA: IEEE, 2006, :895-900. [本文引用:1]
[12] Protter M, Elad M. Image sequence denoising via sparse and redundant representations[J]. IEEE Transactions on Image Processing, 2009, 18(1): 27-35. [本文引用:1]
[13] 蔡泽民, 赖剑煌. 一种基于超完备字典学习的图像去噪方法[J]. 电子学报, 2009, 37(2): 347-350. [本文引用:1]
[14] Zhou Z, Luo L M. Research on image denoising algorithm based on adaptive overcomplete sparse representation theories[J]. Journal of Convergence Information Technology, 2012, 7(16): 315-321. [本文引用:1]
[15] 刘钢. 基于压缩感知和稀疏表示理论的图像去噪研究[D]. 成都: 电子科技大学, 2013. [本文引用:1]
[16] Li M, Zhou G, Zhao B, et al. Radar HRRP adaptive denoising via sparse and redundant representations[C]//Proceedings of the International Symposium on Antennas & Propagation, Nanjing, China: IEEE, 2013: 1094-1097. [本文引用:1]
[17] Deka B, Bora P K. Removal of correlated speckle noise using sparse and overcomplete representations[J]. Biomedical Signal Processing and Control, 2013, 8(6): 520-533. [本文引用:1]
[18] 银壮辰. 基于稀疏表示和字典学习的图像去噪研究[D]. 武汉: 武汉理工大学, 2014. [本文引用:1]
[19] Tang G, Ma J W, Yang H Z. Seismic data denoising based on learning-type over-complete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. [本文引用:1]
[20] 唐刚. 基于压缩感知和稀疏表示的地震数据重建与去噪[D]. 清华大学, 2010. [本文引用:3]
[21] Aharon M, Elad M, Bruckstein A. rmK-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. [本文引用:1]
[22] Bryt O, Elad M. Compression of facial images using the K-SVD algorithm[J]. Journal of Visual Communication and Image Representation, 2008, 19(4): 270-282. [本文引用:1]
[23] 沈鸿雁. SVD地震波场分离与去噪技术在鄂尔多斯盆地地震资料处理中的应用[J]. 地球物理学进展, 2012, 27(5): 2051-2058. [本文引用:1]
[24] 邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. [本文引用:2]
[25] Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the Twenty-Seventh Asilomar—Conference on Signals, Systems and Computers, Pacific Grove, CA: IEEE, 1993: 40-44. [本文引用:1]
[26] Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1994, 41(12): 3397-3415. [本文引用:1]
[27] Smith L N, Elad M. Improving dictionary learning: uultiple dictionary updates and coefficient reuse[J]. IEEE Signal Processing Letters, 2013, 20(1): 79-82. [本文引用:4]