引用本文
张丽美, 成谷. 参数组合优化的随机边界条件及其在地震RTM中的应用[J]. 物探与化探, 2017,41(5): 890-898.
ZHANG Li-Mei, CHENG Gu. Parameterized random boundary condition and its application on seismic RTM[J]. Geophysical and Geochemical Exploration, 2017,41(5): 890-898.
Doi:10.11720/wtyht.2017.5.15  
Permissions
Copyright©2017, 物探与化探编辑部
《物探与化探》编辑部
参数组合优化的随机边界条件及其在地震RTM中的应用
张丽美1, 成谷1,2
1.中山大学 地球科学与工程学院,广东 广州 510275
2.广东省地质过程与矿产资源探查重点实验室,广东 广州 510275
通讯作者: 成谷(1975-),女,副教授,主要研究方向为逆时偏移、全波形反演。Email:chenggu@mail.sysu.edu.cn

作者简介: 张丽美(1990-),女,硕士研究生,主要从事地震资料处理方法和偏移方面的研究工作。

收稿日期: 2016-11-18
基金: 国家自然科学基金青年基金(41004051); 国家高技术研究发展计划(“863”计划)(2013AA092501,2013AA0925010107); 广东省自然科学基金(2016A030313311)
摘要

地震数据叠前逆时偏移(RTM)在高精度成像中具有重要应用,但其对存储量具有极高要求。使用随机边界条件会大大降低逆时偏移的存储成本,文中以自相关函数类型、相关长度、速度扰动标准差3个参数描述的随机介质表达方式来构建参数化的随机边界,对其三参数的意义及取值进行了分析,认为指数型自相关函数、相关长度与波长接近、速度扰动标准差为30%左右为相对优化的随机边界参数组合。模型试验表明,在RTM中采用参数组合优化的随机边界条件能有效破坏人工边界反射波场的相干性,在节省存储量的同时获得较高精度的成像结果。

关键词: 逆时偏移; 随机边界; 随机介质; 波场的相干性
中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2017)05-0890-09
Parameterized random boundary condition and its application on seismic RTM
ZHANG Li-Mei1, CHENG Gu1,2
1.School of Earth Sciences and Engineering,Sun Yat-Sen University,Guangzhou 510275,China
2.Guangdong Key Laboratory of Geological Process and Mineral Resources Exploration,Guangzhou 510275,China
Abstract

Pre-stack seismic reverse time migration has important application in high accuracy subsurface imaging.However enormous memory is needed in RTM.Using random boundary in RTM can reduce memory need of RTM effectively.In this paper,random media expressed by correlation function,correlation length,root mean square velocity perturbation is used,the meanings and values of parameters are analyzed and the optimal parameter group(exponential correlation function,the correlation length being equal to wave length and root mean square velocity perturbation being 30%) are obtained.Numerical simulation shows that using random boundary with optimal parameter group can destroy the coherence of artificial boundary reflection wave fields effectively and obtain high accuracy imaging result with less memory at the same time.

Keyword: reverse time migration; random boundary; random media; coherence of wave field
0 引言

逆时偏移 [1,3]是当前对地下复杂构造进行成像最准确的工具, 但其对存储量有极高的要求。为减少存储成本, 检查点法[4, 5]、边界存储重构法[6, 7]等多种方法被采取。随机边界法[8,10]是一种重要的减少存储成本的方法。Clapp[8]在逆时偏移中使用随机边界条件, 只存储最后两个时间步的波场, 以此递推出整个震源波场, 在适当增加计算量的情况下有效减少了存储成本。采用随机边界条件减少波场的存储成本, 对于三维逆时偏移和全波形反演具有重要意义。

随机边界是在正演模拟中引入的重要概念。在有限差分等地震波数值模拟方法中, 仅能对有限大区域进行模拟, 在人为截断的区域边界处产生的虚假反射波场传回模型内部, 对内部的波场造成干扰。采用边界条件是消除人工边界产生的虚假反射的重要手段。吸收边界条件和随机边界条件是两种重要的边界条件。吸收边界条件是通过某种方式将边界处的波场值吸收或衰减到较小的值, 如单程波传播旁轴近似吸收边界条件[11]和衰减吸收边界条件[12], 完美匹配层(PML)吸收边界条件是最有效的衰减吸收边界条件[13]。随机边界条件是另一类重要的边界条件, 机理与吸收边界条件不同, 它不吸收波场的能量, 而是在边界设置随机速度层, 波场在随机速度层中发生散射, 以此来削弱人工边界反射波场的相干性, 减少人工边界反射波场对成像的影响。随机边界对人工边界反射波场的散射效果越好, 人工边界反射波场的相关性越差, 在使用互相关成像条件后, 对最终的成像结果影响越小。

很多学者对随机边界的构造方式进行了研究。Clapp[8]在边界处的网格点设置随机数来构建随机速度层作为随机边界, 该随机边界条件对随机速度模型缺乏定量和参数化描述, 且无法完全破坏人工边界反射波场的相干性, 在正演模拟、偏移成像结果中均产生噪声和假象 1418。Shen和Clapp[9, 10]通过控制随机边界中的随机速度颗粒的大小和形态两个参数来构建随机边界, 指出在不增加随机边界厚度的情况下, 采用大尺度的、随机形态的随机速度颗粒可以有效散射波场的低频分量。构建随机介质模型是另一种构建随机边界的方式。随机介质模型由大、小两种尺度的非均匀介质组成, 大尺度非均质特性是速度模型的均值速度(背景速度), 小尺度非均质特性是加在背景速度上的随机扰动[19-24] 。奚先和姚姚研究了区域多尺度随机介质模型, 对二维横向各向同性弹性随机介质中的波场特征进行分析[25, 26], 并根据随机过程的谱分解定理, 提出一种局部自相关函数构造各种非平稳随机介质模型的方法[27]。陈可洋提出改进的混合型自相关函数来构造各种随机介质模型的新方法, 灵活构建在各种尺度因子条件下复杂、非均匀、多层的随机介质模型[28]。王金山等提出通过结合多尺度建模技术, 在随机位置或固定位置任意形状截取法来构建随机介质的新方法[29]。李灿苹等利用Von Karm an 型自相关函数模拟随机介质, 分析了不同扰动标准差的模型中速度的分布和变化[30]。殷学鑫模拟了地震波在二维弹性随机介质中的传播, 研究了直达波、反射波、散射波3种分区中, 能量相对值、主频、有效频带宽度3个特征量与随机介质模型的粗糙度因子、自相关长度、扰动标准差等因素的关系[31]。Xie等研究表明在不同方向上的不同相关长度的随机速度模型, 其散射波表现出不同的辐射模式[32]。顾元提出了一种从二维叠后地震数据中估计平稳随机介质参数的方法, 阐述了二维叠后地震数据与随机介质波阻抗模型的关系, 以及随机介质自相关函数参数估计的原理和方法[33]。

文中以Frankel等提出的自相关函数类型、相关长度和速度扰动标准差的参数化随机介质构造方式为基础, 来构建不同参数组合的随机边界, 并对3个参数的取值进行了分析, 得到有效削弱波场相干性的优化参数组合, 最后通过波场重构和RTM来验证该参数组合优化的随机边界条件的有效性, 为在三维逆时偏移和全波形反演中使用参数组合优化的随机边界条件提供依据。

1 三参数表述的随机介质模型构造方式

文中采用三参数表述随机介质的构造方式:

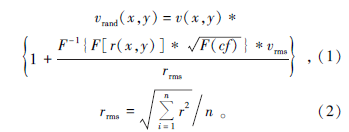
其中, vrand(x, y)是位于(x, y)的随机速度, v(x, y)是背景速度, r(x, y)是随机数。rrms是随机数r(x, y)的均方根值, 如式(2)所示。vrms是速度扰动标准差。F表示傅里叶正变换, F-1表示傅里叶反变换。cf表示自相关函数。自相关函数类型有高斯型(Gaussian), 指数型(Exponential)和自相似型(Self-similar)等[34]。自相关函数及其谱函数的数学表达如表1所示。其中, r代表空间间隔, a代表相关长度, kr代表辐射波数, 二维情况下 kr2为 kx2。K0是零阶修正的Bessel函数。

自相关函数类型、相关长度和速度扰动标准差构成描述随机介质的3个重要参数, 通过修改这3个参数可以构造不同类型的随机介质模型。

表1 随机介质的自相关函数和谱函数[34]
2 随机介质模型参数意义及取值分析

为探究随机边界中参数的意义及不同参数取值对正演模拟结果的影响, 在速度模型四周设置三参数表述的随机速度模型作为随机边界。在固定随机边界层厚度的情况下, 改变自相关函数类型、相关长度和速度扰动标准差3个参数生成不同的随机介质模型, 对随机介质模型的特征及其正演模拟效果进行了分析。

2.1 自相关函数类型

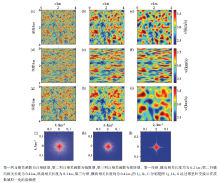
图1横向所示为其他条件相同时, 不同自相关函数类型得出的随机速度模型。模型大小为4 km× 4 km, 背景速度为3 km/s, 速度扰动标准差为10%。图中每一行从左到右随机边界的自相关函数为自相似型、指数型和高斯型。图1j、1k、1l分别是图1g、1h、1i经傅里叶变换后在波数域的归一化的振幅谱。从图1中可以看出, 同一相关长度下, 高斯型自相关函数的随机介质中非均匀性相对集中在低波数(大尺度)部分, 自相似型随机介质具有非常丰富的高波数(小尺度)成分, 指数型模型居中。

图1 不同自相关函数类型及相关长度的随机介质特征

Shen等[9, 10]指出:随机边界中小尺度的随机速度对波场中的高波数分量散射效果好, 大尺度的随机速度对波场的低波数分量散射效果好。3种自相关函数类型的随机介质中, 由于指数型随机介质含有比例适中的高波数和低波数成分, 理论上对各尺度波数分量具有较好的散射效果, 因此可选择指数型自相关函数为优化的自相关函数类型。

2.2 相关长度

从图1中可以看出, 同一种自相关函数的随机介质中, 相关长度越大, 非均匀体越大。沿垂直和水平方向相关长度的比例控制非均匀体形状的纵横比。如图1中第二行所示, 横向相关长度大于纵向相关长度, 速度扰动呈现横向分布的态势。由此可见, 自相关函数的类型和相关长度确定了随机介质中非均匀体的分布和形态。

在吴如山对地震波散射的分类中, 当ka≈ 1时(例如0.1< ka< 10)为广角散射, ka为归一化波数(ka=2π a/λ , k为波数, a为随机介质的相关长度, λ 为波长)。在广角散射的情况下, 非均匀性尺度与波长大小接近, 散射效果最佳, 入射能量被散射到各个方向, 称为“ 共振散射” 或“ Mic散射” [35]。据此可知, 随机介质对地震波散射效果与相关长度的大小有密切的关系。

图2为不同相关长度的指数型随机边界模型(速度扰动标准差为20%)在0.75 s时刻的波场快照。正演模拟基于声波方程, 采用时间2阶空间8阶有限差分算子, 记录时长为0.75 s, 时间步长为 0.25 ms。震源是主频为40 Hz的雷克子波, 位于模型的正中间。图2a为相关长度为0.004 km的随机边界条件下的波场快照, 图2b为相关长度为0.075 km的随机边界条件下的波场快照。本模型中地震波的主波长为0.075 km。图2a、2b相比可以看出, 当随机介质的相关长度与波长相近时, 随机边界对人工边界反射波场的散射效果较好。

图2 不同相关长度下0.75 s时刻的波场快照

2.3 速度扰动标准差

图3a所示为自相关函数为指数型, 纵横向相关长度均为0.4 km的条件下, 不同速度扰动标准差的随机介质形态, 左图速度扰动标准差为10%, 右图速度扰动标准差为30%, 图3b所示为过图3a中心的水平剖面, 可以看出左图的速度起伏小, 右图的速度起伏大。其余参数固定的情况下, 速度扰动标准差不影响随机速度扰动分布的形态, 只影响速度扰动大小, 速度扰动标准差越大, 随机速度扰动越大, 即速度扰动标准差表示随机速度起伏与背景速度之间的相对比例。

图3 不同速度扰动标准差的随机介质形态和过中心的水平剖面

图4展示的是不同速度扰动标准差的指数型随机介质(相关长度为0.075 km)作为随机边界, 在 0.75 s时刻的波场快照和过波场中心的横向和纵向剖面, 速度扰动标准差从上至下依次是10%、20%、30%。如图4所示, 速度扰动标准差为10%的随机边界对人工边界反射波场的散射效果较差, 人工边界反射波场的相干性仍较强, 波前仍连续清晰, 波场能量仍集中在波前面。当速度扰动标准差增大至20%时, 随机边界对波场的散射作用增强, 人工边界反射波场的波前能量占优情况减弱, 波前面连续性变差但仍可辨识, 波场能量扰动增大。当速度扰动标准差增大至30%时, 人工边界反射波场的相干性被有效削弱, 波前不再可辨认, 波场能量扰动大。随着随机边界速度扰动标准差的增加, 散射波场的能量(振幅的平方)最大值随之减小:图4a中波场的最大振幅约为6× 105, 图4c中波场的最大振幅约为5× 105, 图4e中波场的最大振幅约为4× 105, 表明人工边界反射波前的能量越来越弱, 即随机边界对人工边界反射波场的散射效果增强。

因此可得, 固定其余参数, 增大速度扰动标准差, 对波场的散射效果增强, 能显著削弱人工边界反射波场的相干性和波前的连续性, 但受到有限差分法的稳定性约束, 速度扰动标准差不能过大, 在本模型中, 速度扰动标准差在30%附近为佳。

图4 不同速度扰动标准差下0.75 s时刻的波场快照和过波场中心的横向和纵向剖面

3 参数组合优化的随机边界在RTM中的应用

在逆时偏移成像中, 随机边界既是波场正传时减弱人工边界反射的手段, 也是减少逆时偏移存储量的重要方式, 因此, 文中从波场重构及成像效果方面测试了参数组合优化的随机边界条件在逆时偏移中的应用。

3.1 利用随机边界重构波场

逆时偏移中, 由于震源波场与检波点波场在延拓时间方向上不一致, 因此需要保存二者之一(以震源波场为例)的全部或部分时刻的波场。采用有效边界存储策略可减少波场的存储量, 但仍需对波场的边界值进行保存, 在三维情况下其存储量十分巨大[36]。使用随机边界, 只需存储最后两个时间步的震源波场, 即可逆时延拓重构出所有时刻的震源波场, 避免了对波场的存储。

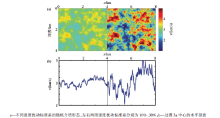
图5所示为不使用边界条件及使用参数组合优化的随机边界条件下的正传波场、重构波场及其二者的差。图5a为层状均匀速度模型, 两层速度分别为2.5、3.5 km/s。震源的深度是0.020 km, 随机边界厚度为50个网格点。图5b、5c和5d分别为不使用边界条件下在0.55 s时刻的正传波场、重构波场及二者(图5b、5c)之间的差。图5e、5f和5g分别为使用参数组合优化的随机边界条件, 在0.55 s时刻的正传波场、重构波场及二者(图5e、5f)之间的差。数值结果表明, 重构波场与原始波场之间的差(图5d、5g)比原始波场(图5b、5e)小10个数量级, 因此可认为利用逆时延拓可实现对波场的精确重构。但不同的是, 不使用边界条件进行重构, 波前到达边界处会产生具有相干能量的反射(如图5b中箭头所示)进而在成像过程中产生假象。而利用参数组合优化的随机边界进行重构, 随机边界极大程度地破坏边界反射波场的相干性, 边界反射波场发生散射形成随机波场(如图5e中箭头所示), 而这些随机的波场能够在多炮叠加过程中被相互压制抵消。

图5 逆时延拓重构的波场

3.2 参数组合优化的随机边界条件用于成像

图6为不同边界条件下得到的层状模型单炮成像结果, 所用模型与图5a相同。炮点位于地表1.5 km处, 检波器位于地表的所有网格点。图6a为不使用边界条件RTM方法得到的单炮成像结果, 由边界反射产生的波场导致在0.7 km处产生假象(如图6a中箭头所示)。这些具有相关性的能量在多炮叠加中会相干增强, 在最终的成像结果中产生假象。图6b为利用参数组合优化的随机边界RTM方法得到的单炮成像结果, 由于随机边界的散射效果, 人工边界反射能量相干性被削弱, 在浅层产生随机的成像噪声, 换言之, 参数组合优化的随机边界将图6a中的假象(如图6a中箭头所示)“ 粉碎” 成随机噪声(如图6b中箭头所示)。图6c为利用PML边界条件通过存储波场得到的成像结果, 由于PML边界吸收了边界反射波场, 成像结果中没有因边界反射造成的假象。因此, 单炮的成像结果中以PML边界条件为优, 但以更多的存储量为代价。

图6 利用不同边界条件的单炮成像结果

RTM的成像结果为多炮成像结果的叠加, 因此利用随机边界条件, RTM单炮成像结果中的随机噪声在多炮叠加中相互抵消, 最终压制为可忽略的噪声。图7a为利用参数组合优化的随机边界得到的多炮叠加成像结果, 值得注意的是, 浅层的随机噪声由于多炮叠加被相互抵消压制至可忽略的程度。作为对比, 图7b展示了利用PML边界条件得到的成像结果。可见, 利用参数组合优化的随机边界条件可获得与利用PML边界条件精度相近的成像结果。

图8展示了复杂模型中使用参数组合优化的随机边界条件和PML边界条件的成像结果。图8a为SEG盐丘模型, 模型大小为15.700 km× 3.660 km, 网格间距为0.012 km。模型横向网格点数Nx=1 288, 纵向网格点数Ny=300, 检波器位于炮点左侧, 测线长度为4.270 km, 检波器间隔为 0.024 km。炮点位置从0~15.700 km, 炮点间距 0.049 km, 总炮数M=325, PML边界和随机边界均为50个网格点, 厚度为0.610 km。时间步长为 1 ms, 总共5 s, 时间步长总数L=5 000。

图7 多炮叠加的成像结果

图8 不同边界条件下SEG 盐丘模型逆时偏移成像结果

使用随机边界条件, 首先震源波场正传一次(只存储最后两个时间步长的波场), 检波点波场反传, 存储的波场反传重构震源波场, 需要计算3次波场传播。使用PML边界条件首先震源波场正传, 存储所有时间步长的波场, 在检波点波场反传过程中提取存储的正传波场应用成像条件, 需要计算两次波场传播。使用PML边界条件和随机边界条件在波场传播方面计算量是3∶ 2的关系。利用Openmpi并行技术, 新增的计算量对计算效率影响不大。但在所需存储量方面(表2), 使用PML边界条件存储所有时间步长的完整波场所需存储量约为 2 339.11 G, 计算如式(3):

MemoryPML=Nx×Ny×L×M×4byte。(3)

使用检查点法或者边界存储重构法能减少波场的存储量, 但也需要存储每个时间步长的部分波场, 在三维情况下存储量依旧巨大。使用参数组合优化的随机边界条件的存储量为0.94 G, 计算如式(4):

Memory随机边界=Nx×Ny×2×M×4byte。　(4)

可见, 使用参数组合优化的随机边界在适当增加计算量的情况下可获得与PML边界条件精度相当的成像结果, 并且有效降低了对波场的存储需求, 在三维情况下更具优势。

表2 使用PML边界和随机边界条件下存储量对比
4 结论

文中以自相关函数类型、相关长度和速度扰动标准差三参数描述的随机边界构造方式为基础, 对三参数的意义及取值进行了分析, 得到结论如下:

1)指数型自相关函数的随机介质与其他两种类型(自相似型和高斯型)相比含有适中的高波数和低波数成分, 对波场中的高、低波数成分均有较好的散射效果。可选择指数型自相关函数类型作为优化的随机边界参数。

2)当随机介质的相关长度与波长相当时, 随机边界对波场的散射效果较好, 对人工边界反射波场相干性的破坏最强。可选择与波长相当的相关长度作为优化的随机边界参数。

3)速度扰动标准差增大时, 对人工边界反射波场的相干性和波前连续性的破坏增强。但受到有限差分方法稳定性的约束, 速度扰动标准差亦不易过大。可选择速度扰动标准差为30%左右为优化的随机边界参数。

以上述分析为基础, 文中从波场重构及成像效果方面测试了参数组合优化的随机边界条件在RTM中的应用。模型实验表明:参数组合优化(指数型自相关函数, 相关长度与波长相当, 速度扰动标准差为30%左右)的随机边界条件能实现精确的波场重构, 同时在极大降低波场存储成本的前提下得到与PML边界条件精度相近的成像结果。随机边界条件的这一特性适用于所有时间域基于波场互相关计算的方法, 如逆时偏移、全波形反演、最小二乘偏移等, 其应用可进一步扩展。本文实验主要针对二维模型进行, 在三维情况下随机边界条件在保证精度前提下对减少存储量具有更重要的意义。

致谢:感谢陈波博士富有成果的讨论和建议。感谢国家留学基金委资助。

The authors have declared that no competing interests exist.

参考文献
[1] Whitmore N D. Iterative depth migration by backward time propagation[C]//Expand ed Abstracts of the 53rd Annual SEG Meeting. Las Vegas, Nevada: Society of Exploration Geophysicists, 1983: 382-385. [本文引用:1]
[2] McMechan G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983, 31(3): 413-420. [本文引用:1]
[3] Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. [本文引用:1]
[4] Griewank A. Achieving logarithmic growth of temporal and spatial complexity in reverse automatic differentiation[J]. Optimization Methods and software, 1992, 1(1): 35-54. [本文引用:1]
[5] Symes W W. Reverse time migration with optimal checkpointing[J]. Geophysics, 2007, 75(5): SM213-SM221. [本文引用:1]
[6] Gauthier O, Virieux J, Tarantola A. Two-dimensional nonlinear inversion of seismic waveforms: Numerical results[J]. Geophysics, 1986, 51(7): 1387-1403. [本文引用:1]
[7] Tan S R, Huang L J. Reducing the computer memory requirement for 3D reverse-time migration with a boundary-wavefield extrapolation method[J]. Geophysics, 2014, 79(5): S185-S194. [本文引用:1]
[8] Clapp R G. Reverse time migration with rand om boundaries[C]//Expand ed Abstracts of the 79th Annual SEG Meeting. Houston, Texas: Society of Exploration Geophysicists, 2009. [本文引用:2]
[9] Shen X, Clapp R G. Rand om boundary condition for low-frequency wave propagation[C]//Expand ed Abstracts of the 81st Annual SEG Meeting. San Antonio, Texas: Society of Exploration Geophysicists, 2011, 30: 2962-2965. [本文引用:2]
[10] Shen X K, Clapp R G. Rand om boundary condition for memory-efficient waveform inversion gradient computation[J]. Geophysics, 2015, 80(6): R351-R359. [本文引用:2]
[11] Clayton R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bulletin of the seismological society of America, 1977, 67(6): 1529-1540. [本文引用:1]
[12] Cerjan C, Kosloff D, Kosloff R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708. [本文引用:1]
[13] Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of computational physics, 1994, 114(2): 185-200. [本文引用:1]
[14] 李博, 刘红伟, 刘国峰, 等. 地震叠前逆时偏移算法的CPU/GPU实施对策[J]. 地球物理学报, 2010, 12: 2938-2943. [本文引用:1]
[15] 胡昊, 刘伊克, 常旭, 等. 逆时偏移计算中的边界处理分析及应用[J]. 地球物理学报, 2013, 56(6): 2033-2042. [本文引用:1]
[16] 石颖, 柯璇, 张莹莹. 逆时偏移边界条件与存储策略分析[J]. 地球物理学进展, 2015, 30(2): 581-585. [本文引用:1]
[17] Shi Y, Wang Y H. Reverse time migration of 3D vertical seismic profile data[J]. Geophysics, 2016, 81(1): S31-S38. [本文引用:1]
[18] 张慧宇, 王立歆, 孔祥宁, 等. 适于大规模数据的逆时偏移实现方案[J]. 物探与化探, 2015, 39(5): 978-984. [本文引用:1]
[19] Ikelle L T, Yung S K, Daube F. 2-D rand om media with ellipsoidal autocorrelation functions[J]. Geophysics, 1993, 58(9): 1359-1372. [本文引用:1]
[20] 奚先, 姚姚. 二维随机介质及波动方程正演模拟[J]. 石油地球物理勘探, 2001, 36(5): 546-552. [本文引用:1]
[21] Kerner C. Anisotropy in sedimentary rocks modeled as rand om media[J]. Geophysics, 1992, 57(4): 564-576. [本文引用:1]
[22] Korn M. Seismic waves in rand om media[J]. Journal of applied geophysics, 1993, 29(3-4): 247-269. [本文引用:1]
[23] Ergintav S, Canitez N. Modeling of multi-scale media in discrete form[J]. Journal of seismic exploration, 1997, 6(1): 77-96. [本文引用:1]
[24] Flatté S M, Wu R S. Small-scale structure in the lithosphere and asthenosphere deduced from arrival time and amplitude fluctuations at NORSAR[J]. Journal of Geophysical Research: Solid Earth, 1988, 93(B6): 6601-6614. [本文引用:1]
[25] 姚姚, 奚先. 区域多尺度随机介质模型及其波场分析[J]. 石油物探, 2004, 43(1): 1-7. [本文引用:1]
[26] 奚先, 姚姚. 二维横各向同性弹性随机介质中的波场特征[J]. 地球物理学进展, 2004, 19(4): 924-932. [本文引用:1]
[27] 奚先, 姚姚. 非平稳随机介质模型[J]. 石油地球物理勘探, 2005, 40(1): 71-75. [本文引用:1]
[28] 陈可洋, 刘洪林, 杨微, 等. 随机介质模型的改进方法及应用[J]. 大庆石油地质与开发, 2008, 27(5): 124-126, 131. [本文引用:1]
[29] 王金山, 陈可洋, 吴清岭, 等. 随机介质模型的一种构造方法[J]. 物探与化探, 2010, 34(2): 191-194. [本文引用:1]
[30] 李灿苹, 王南萍, 李志宏. Von Karman 型自相关函数模拟随机介质[J]. 物探与化探, 2010, 34(1): 98-102. [本文引用:1]
[31] 殷学鑫, 刘洋. 二维随机介质模型正演模拟及其波场分析[J]. 石油地球物理勘探, 2011, 46(6): 862-872. [本文引用:1]
[32] Xie X B. Seismic wave scattering in 3D rand om media: A finite-difference simulation and slowness domain analysis[C]//Expand ed Abstracts of the 83rd Annual SEG Meeting. Houston, Texas: Society of Exploration Geophysicists, 2013: 3428-3432. [本文引用:1]
[33] 顾元, 朱培民, 李辉, 等. 二维叠后地震数据的平稳随机介质参数估计[J]. 地球物理学报, 2014, 57(7): 2291-2301. [本文引用:1]
[34] Frankel A, Clayton R W. Finite difference simulations of seismic scattering: Implications for the propagation of short-period seismic waves in the crust and models of crustal heterogeneity[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B6): 6465-6489. [本文引用:1]
[35] 吴如山. 地震波散射: 理论与应用[J]. 地球物理学进展, 1989, 4(4): 1-23. [本文引用:1]
[36] 王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 2412-2421. [本文引用:1]