TEM中心回线电动势响应换算磁场响应求解全区视电阻率及1-D直接反演的实用方法

引用本文

蒋邦远, 杜庆丰. TEM中心回线电动势响应换算磁场响应求解全区视电阻率及1-D直接反演的实用方法[J]. 物探与化探, 2017,41(4): 758-768.
JIANG Bang-Yuan, DU Qing-Feng. Applied processing for calculation of TEM in-loop full-zone apparent resistivity and 1-D inversion of field transferred from d B/d t response observed directly [J]. Geophysical and Geochemical Exploration, 2017,41(4): 758-768.
Doi:10.11720/wtyht.2017.4.28 复制到剪切板

Permissions

《物探与化探》编辑部

TEM中心回线电动势响应换算磁场响应求解全区视电阻率及1-D直接反演的实用方法

蒋邦远, 杜庆丰

中国地质科学院地球物理地球化学勘探研究所,河北廊坊 065000

作者简介: 蒋邦远(1931-),男,教授级高工,享受国务院政府特殊津贴,1952年南京大学物理系毕业,长期从事电磁法研究。

收稿日期: 2017-03-01

摘要

中心回线圴匀大地电动势响应(d B/d t)的解有三种:唯一解、双解及无解,若是层状大地,尚有“上凸”、 “下凹”的假异常现象,而磁场响应( H_z)则无此类情况,但若想直接观测 H_z则需添加设备。本文以理论为基础,从实践经验出发,设计出一套将d B/d t转换为 H_z的方案,该方法不苛求观测的最晚延时达到近带;同时,提出了求视深度的经验改正系数,以及新的高精度后沿改正法。这一套方法不仅可换算出 H_z,还能求出全区视电阻率及1-D反演数据。实例表明本方法实用有效。

关键词: 电动势响应; 磁场响应; 视深度计算; 全区视电阻率; 高精度“ 等效延时改正法”; 反演

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2017)04-0758-11

Applied processing for calculation of TEM in-loop full-zone apparent resistivity and 1-D inversion of field transferred from d B/d t response observed directly

JIANG Bang-Yuan, DU Qing-Feng

Institute of Geophysical and Geochemical Exploration,CAGS,Langfang 065000,China

Abstract

The voltage response(d B/d t)is wildly used in TEM in-loop configuration; nevertheless, for layered earth,it has several defects in solution, such as unique valued, dual-valued, undefined valued and overshoot and undershoot phenomena. It is hoped that field response has not these defects. So if we want to observe field response directly,SQUID or flux-gate sensor should be added. Therefore the process of transferred d B/d t should be available. Of course it has some other difficult problems in calculation, for examples: how to get the first electromagnetic field strength and applied apparent depth formula. This paper tackles those problems and has solved them.

Keyword: electrodynamic force; magnetic field strength; applied apparent depth formula; whole area apparent resistivity; equivalent effect delay time correction; inverting

Show Figures

0 引言

瞬变电磁法激发大地产生的涡流在地面上产生二次磁场, 但由于技术原因, 长期以来观测的是磁场对时间的微分, 即感应电动势响应dB/dt, 而不是磁场强度(H_z)本身。均匀半空间的dB/dt的理论解有3种:唯一解、双解及无解, 对于层状大地, 还会出现“ 上凸” (overshoot)及“ 下凹” (undershoot)现象, 以致数据处理与解释困难。此外, 两者近带响应衰减特征明显不同(H_z∝ t^-3/2, dB/dt∝ t^-5/2), 故而在功率— 灵敏度相同条件下, 前者的勘探深度大很多。国内外专家开展了超导探头及磁通门探头的研制, 以及将dB/dt换算为H_z的研究。在国内, 两种探头都已研制成功, 但应用尚不够广泛; 就换算H_z而言, 目前主要用在电偶源探测深部构造上。专门论述中心回线换算的论文鲜见报导, 笔者则专就此换算方法做了深入研究。

就理论而言, 将非连续观测的电动势转换为磁场, 最基本的要求是从正常场向早期延时递推。然而, 中心回线装置主要是探测导电层, 而在探测深度内往往有多个导电层, 以致最后的延时难以确保已在正常场区域, 即使研究的方法正确, 可以应用的普遍性也较低。瞬变场的频谱特性随时间而改变, 故而勘探深度有数种定义, 有多个勘深表达式, 而实用的表达式是乘以经验系数(0.441)的表达式, 据此推测, 适用于磁场勘深的表达式也必然需乘以经验系数, 而现在尚无此类公式出现。在理论指导下, 经反复思考, 通过大量模型的计算分析验证, 形成以下计算方案:“ 同值, 异时, 似深” 。此方案化解了上述难题, 其适用范围与dB/dt的适用范围一致, 即中— 近区。粗放地说, dB/dt成果合格, 则H_z的成果也相应合格。实例计算证明如此。

1 dB/dt递推H_z求全区视电阻率ρ _f及1-D 反演

1.1 由电动势dB/dt递推磁场强度H_z

实测电动势是非连续的, 故由dB/dt求取H_z唯有采用递推的算法:

$\begin{matrix} H_{z, i - 1} = \frac{(ε_{i} ε_{i - 1})^{\frac{1}{2}}}{μ_{0} I N_{T} A_{R} 1000} \cdot \frac{(t_{i} - t_{i - 1})}{1000} + H_{z, i}, (1) \end{matrix}$

式中:H_z为磁场强度(A/m), ε 为电动势(mV), t为釆样延时(ms), μ ₀为真空磁导率, A_R为接收线圈等效面积, N_T为发射回线匝数, i为取样延时道数。

式(1)为由晩延时向早延时递推的表达式。由于递推误差的原因, 若设精度应小于2%, 递推应到τ ₀≤ 0.01, 即中、远区分界处。为研究需要, 还可以由远区向近区递推, 该表达式为

$\begin{matrix} H_{z, i} = H_{z, i - 1} - \frac{(ε_{i} ε_{i - 1})^{\frac{1}{2}}}{μ_{0} I N_{T} A_{R} 1000} \frac{(t_{i} - t_{i - 1})}{1000} 。 (2) \end{matrix}$

1.2 H_z_,_n-₂的求取前提

设实测数据达到精度要求的取样延时为t_n, 如何求式(1)中的最晚的H_z_,_i, Levy G.M^[1]提出计算延时处至少应有3个延时的数据成一直线, 延时t的参数n> 2, 实质就是要求接近正常场。此要求是合理的, 但是金属矿区若有多层矿带则此要求很难达到。

磁场强度较电动势衰减慢, 若电动势数据已属正常场, 磁场数据早已位于正常场。根据大量模型计算统计得出一重要思路:将用第n道电动势ε _n求出的全区视电阻率当作由n-2道磁场强度计算出的全区视电阻率, 而后反求, 得到n-2道的磁场, 即H_z_,_n-₂。此思路称之为“ 同值, 异时” 。据此, 对近区数据推导出式(3), 利用n道的电动势ε _n即可求出H_z_,_n-₂:

$\begin{matrix} H_{z, n - 2} = \frac{2 ε_{n}}{3 μ_{0} A_{R}} \frac{t_{n}^{\frac{5}{2}}}{t_{n - 2}^{\frac{3}{2}}} 。 (3) \end{matrix}$

式(2)中H_z_,_i-₁的求法与上述求法类似。设第一道延时为t₁, 则先求出第三道dB/dt之ρ _f, 将此ρ _f当作第一道磁场强度求出之值, 再用它反求磁场强度H_z_,_i。

1.3 “ 似深度”

H_z的视深度与dB/dt的视深度大致相等称之为“ 似深度” 。视深度与很多参数有关, 且有很多定义, 就dB/dt的视深度而言, 有扩散深度、分辨深度、显深度等。广为应用的视深度公式是根据“ 烟圈” 理论推出并乘以经验系数0.441得出的, 但该式不适用于全区, 比如远区。据此推测, H_z的视深度公式也会具有此种特征。用中国地质大学(武汉)孟教授所编的VCTEM1D 应用软件做了大量模型计算, 其结果较模型的深度参数偏深较大。反推其所用视深度公式, 相当于d_a=40 $\begin{matrix} \sqrt{ρt} \end{matrix}$ , 由此断定适用磁场的视深度公式也必须乘以经验系数。经分析归纳, 总结出普遍适用的系数k=0.875, 因此似深度公式为

$\begin{matrix} d_{a} = 35 \sqrt{ρ_{f} t} 。 (4) \end{matrix}$

式(4)不适用于远区, 对中— 远区的深度计算也偏深。因此, 合理的工作设计应将探测目的物处于中— 近区和近区, 则式(4)可适用于大多数情况。若实测数据已在中— 远区, 则k系数调整至k≈ 0.825较为合适。

1.4 由H_z求全区视电阻率ρ _f

将Hohmann和Ward公式(该式中用圆形发射回线及电导率参数, 与国内习惯用法不同)^[2]

$\begin{matrix} H_{z} = \frac{1}{θ^{2} a^{3}} [(\frac{θ^{2} a^{2}}{2} - \frac{3}{4}) \erf (θa) + \frac{3 θa}{2 \sqrt{π}} e^{- θ^{2} a^{2}}] \end{matrix}$

改写为

$\begin{matrix} \begin{matrix} H_{z} = \frac{\sqrt{π}}{2 L} [(1 - \frac{3}{2} \frac{1}{u^{2}}) \erf (u) + \frac{3}{\sqrt{π}} \frac{1}{u} e^{- u^{2}}] \\ = \frac{\sqrt{π}}{2 L} f (u), (5) \\ f (u) = H_{z} \frac{2 L}{\sqrt{π}}, (6) \\ u = (\frac{L}{100}) / \sqrt{ρ_{f} t} 。 (7) \end{matrix} \end{matrix}$

式中L为发射回线边长。需特别说明, 式(5)及式(7)中, I、N_T及A_R在递推的H_z中已包含, 故公式中无显示。

应用式(5)的方法为众所周知的试错法(try and test), 或利用事先计算好的f(u)— u数据表查表。两种算法因无归一问题, 计算简易。对远区的H_z也可代入远区渐近式来计算视电阻率:

$\begin{matrix} ρ_{a} = \frac{μ_{0} L^{3}}{3 π \sqrt{π} t} (\frac{\sqrt{π}}{2 L} - H_{z}) 。 (8) \end{matrix}$

1.5 1-D直接快速反演

1-D反演要求数据有很高的精度。一般来说, ρ _f曲线已达到圆滑, 但1-D反演往往还不够圆滑。故下述模型计算都做1-D反演, 以从严验证文中计算思路的合理性及实用性, 而不是仅计算全区视电阻率。所用公式如下:

(i) 简化“ 烟圈” 公式^[3]

$\begin{matrix} ρ_{r} = 4 {[\frac{(\sqrt{ρ_{i + 1} t_{i + 1}} - \sqrt{ρ_{i} t})}{t_{i + 1} - i_{i}}]}^{2} \sqrt{t_{i} t_{i + 1}}; (9) \end{matrix}$

(ii) 经验式^[4]

$\begin{matrix} \begin{matrix} ρ_{e} = \sqrt{ρ_{i} ρ_{j}} {[\frac{n_{ij}}{1.5}]}^{c}, (10) \\ n_{ij} = 1.5 \frac{\ln (ρ_{j} / ρ_{i})}{\ln (t_{j} / t_{i})} + 1.5, j = i + 1 。 (11) \end{matrix} \end{matrix}$

式(9)~(11)中的各电阻率都是指全区视电阻率, 而文中的ρ _f特指由H_z计算得到的全区视电阻率。

2 模型计算

2.1 阶跃波

2.1.1 均匀半空间递推H_z的基础特性

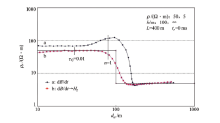
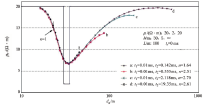
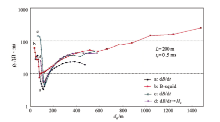
此模型的有关参数乃精心设计, 图1中的横坐标(t)也可用综合参数τ ₀表示, 两者数值相同。图中还标出曲线对应的区带, 曲线特征一目了然。图中4条曲线的取样延时步长t_i+₁/t_i为1.25。步长愈大递推数据误差愈大, 现在应用较广的仪器中步长最大为1.26, 一般为1.2; 文中选1.25系从严要求。

图中a曲线为利用式(1)求出的H_z_,_i-₁计算出的全区视电阻率ρ _f。计算从t=10 ms起向远区递推, ρ _f在0.1 ms< t< 10 ms之间是一恒定的值; t> 0.1 ms后ρ _f逐渐増大, 在第13取样延时(t₁₃=0.014 6 ms), ρ _f=1.017 Ω · m, 误差1.7%; 而后急速上升, 第一取样道(t₁=0.001 ms), ρ _f=1.29 Ω · m, 误差达29%。

b曲线为利用式(2)求出之H_z_,_i计算出的ρ _f, 其曲线特征大致相当a曲线的二次镜像, 镜面位于ρ _f=1 Ω · m的“ 横镜” 及t=0.1 ms的“ 直镜” 。t₃₀=0.646 ms的ρ _f=0.98 Ω · m, 误差2%, 与a曲线的t₁₃道误差略同。而后曲线快速下降, 下降幅度大大超过a曲线之上升幅度。

c曲线是将H_z_,_i代入式(8)得出的, 其t₁₉=0.056 ms的全区视电阻率误差为2%, 故只适用于远区。

d曲线是将H_z_,_i-₁代入式(6) 得出的f(u)函数与延时t的关系曲钱。此曲线绘于图1是为有利于对比分析a、b曲线位于f(u)为何值处相连接为最佳。

综上所述, 公式(1)可应用于中、近区, 严格地说应是τ ₀≥ 0.015; 公式(2)可用于远区、中区, 严格地说应在0.001≤ τ ₀≤ 0.64范围内。如果欲计算的数据涉及全区, 则需在f(u)=0.85处将式(1)与式(2)计算之数据相连接。

	Figure Option View Download New Window
	图1 均匀半空间不同参数的ρ _f— t特性曲线

2.1.2 递推H_z与dB/dt计算之ρ _r特性对比

2.1.2.1 D型二层大地

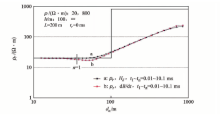
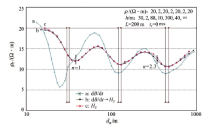
设计发射回线边长L=400 m, 延时从远区算到近区, 两地层交界面靠近中区n=1处。dB/dt及H_z计算曲线绘于图2。图中n=1为dB/dt中区归一之处, 致使计算之ρ _r数据不仅出现“ 上凸” 假高阻, 且使第一层的ρ _r偏高, 以及反映边界的曲线下降部分偏深很多。而由H_z计算之ρ _r曲线与模型较一致, 无“ 上凸” 假高阻异常, 曲线下降之转折点约在二层交界位置。另外, τ ₀< 0.01的时段误差增大, ρ _r逐渐偏低, 与均匀半空间的特点一致。

	Figure Option View Download New Window
	图2 D型二层大地H_z与dB/dt之ρ _r— d_a的对比曲线

需要说明:图中n=1不是按磁场数值而是按电动势数值计算的, 因为H_z是由dB/dt递推而来。

2.1.2.2 G型二层大地

图3为此模型计算一例。图中除b曲线有明显的“ 下凹” 假低阻异常外, 其余曲线特征基本一致。

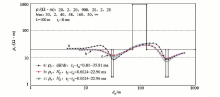
	Figure Option View Download New Window
	图3 G型二层大地ρ _r— d_a曲线对比

2.1.2.3 HKH七层大地

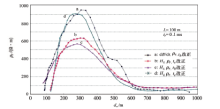
此七层大地模型将H、K三层大地之ρ _r特性及相互影响的情况皆包括其中。图4中dB/dt计算之曲线a对应第一低阻层有典型的“ 上凸” 假高阻异常, 而第二低阻层的“ 上凸” 假高阻与第四高阻层异常相连接, 使高阻层显得很宽; 如若此为野外观测结果, 则可能产生误解。而递推H_z计算的曲线b则无此类问题, 对模型反映得清楚、明确。

	Figure Option View Download New Window
	图4 HKH七层大地3种1-D反演ρ _r— d_a曲线对比

b曲线亦有缺点, 异常幅度较低。利用式(10)计算出的曲线c弥补了此缺点。

2.1.3 递推H_z的应用区带

前文中已明确说明, 由近区向远区递推之H_z因精度问题, 最早只能到τ ₀=0.01对应的延时。而τ ₀受多个参数影响, 就实际工作而言可改变的参数仅有发射回线边长L, 故将其作为分析重点。

图5为按相似准则设计的模型。4种模型边长中, L_min=50 m, L_max=400 m。计算的4个模型的1-D ρ _r曲线特点完全一致, 特别是ρ _r_min的视深度与模型低阻带中心的误差仅为0.3%, 曲线非常圆滑。

	Figure Option View Download New Window
	图5 近区低阻层ρ _r— d_a曲线

上述特点完全可以反映在另一组符合相似准则的模型中, 可以想象, 只要发射边长选择恰当就会取得良好成果。但是欲探测的低阻目的物的视深度若浅于中— 近区, 情况将会改变。

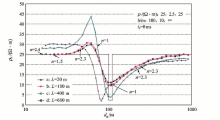
将图5中的第三个模型的发射边长改为20、400和600 m, 其计算结果见图6。为达到t₁≥ 0.01 ms及τ ₀(t₁)≥ 0.015的要求, 图中3条曲线的起始延时不同。3种边长的视电阻率极小(ρ _r_min)对应的视深度d_a分别为104.4、116.6、118.9 m, 而L=200 m对应的d_a=105.2 m(见图5)。图6上还标出了n=1及n=2.3的位置。

	Figure Option View Download New Window
	图6 发射回线不同、低阻层位于不同区带之ρ _r— d_a曲线

这些数据表明:低阻层由位于近区改为临近中区(n=1), 视深度增大, 若低阻层位于中— 远区则误差更大。因此, 当n=1对应的视深度大于ρ _r_min对应的视深度时, 就可判断低阻层位于中— 远区, 而勘探深度计算不准, 其结果偏深。

图7为4种边长下用dB/dt计算的ρ _r曲线, 图中d曲线(L=600 m)ρ _r_min对应的视深度d_a=81.2 m; 图6中c曲线的d_a=118.9 m。而其模型值为105 m, 可见这2个结果一浅一深, 精度都较差。

根据瞬变场的波谱特性及在大地中的传播特性可知, 只用一个勘深公式求取全区的视深度是不适当的。常用的d_a=28.08 $\begin{matrix} \sqrt{ρ_{a} t} \end{matrix}$ 及本文的公式(4)主要适用于近区, 故图6出现的视深度随边长L变化的特点是必然的, 而图7中d曲线的低阻异常勘深太浅主要是归一化的原因, 它将低阻带全处于中— 远区, 以致深度变浅。

	Figure Option View Download New Window
	图7 发射回线不同、低阻层位于区带不同、由dB/dt计算出的ρ _r— d_a曲线

2.1.4 递推起点t_n的影响

前已述及, Levy G. M对递推起点的要求n≥ 2 是合理的, 但适用性较差, 因而可认为认识不全面。举例分析如下。

2.1.4.1 H型三层大地

此模型低阻层位于中— 近区, 用4个不同的t_n

递推H_z计算ρ _r曲线(图8)。由图中曲线特征归纳出t_n不同对递推算法之曲线有如下特征:

1)如以t_n最长的d曲线为“ 标准” , 其余3条曲线的尾端都偏离了“ 标准” 位置, 但b、c、d曲线t_n相应之n都大于2。

2)偏离程度与t_n值没有直接联系。a曲线t_n值最小但偏离最小; 不论偏离情况如何, 低阻层异常反映相同。a曲线t_n=0.142 ms, n=1.64, 此t_n值比实际工作釆用值小太多, n值也小于2。

2.1.4.2 HHH七层大地

	Figure Option View Download New Window
	图8 递推起点t_n不同之ρ _r— d_a曲线

此模型有3个低阻层, 第一层位于中— 远区, 第二层位于中区, 第三层位于近区。选4种起始延时t_n, 计算结果如图9所示。此组曲线中, a、b曲线相似度最高; c曲线尾部偏差较大; 而d曲线局部与a曲线基本重合, 但首部则偏高, 不过它的t_n=0.15 ms, 这完全是为研究分析而算, 实际工作中不可能釆用, 再者其n=1.23, 小于2。

	Figure Option View Download New Window
	图9 HHH七层大地起始递推延时t_n不同之ρ _r— d_a曲线

2.1.5 递推H_z与直接计算的H_z计算ρ _r对比

直接计算的H_z是用孟教授所编程序计算得出, 但该程序的反演方法与本文所用不同。必须说明, 为对比条件一致, 图10中a、 b曲线都是用式(9)与式(5)计算。

图中b、c曲线特征基本一致, 仅3处有较明显差别:c曲线第一延时的ρ _r≈ 20 Ω · m, 但从曲线斜率判断其更早延时之ρ _r将大于20 Ω · m, 而b曲线ρ _r< 20 Ω · m已趋于正常场; c曲线t_n之ρ _r大于b曲

	Figure Option View Download New Window
	图10 HHH七层大地三种参数的1-D反演ρ _r— d_a曲线

线t_n之ρ _r, 但差值不大; 在n=2.3(中区与近区分界线, 相当τ ₀=1)附近, b、c曲线相差明显, 但两者都圆滑。总之, 仅此3点有差异但不大, 且基本特征一致, 完全可以认为本文递推之H_z是合格的、适用的。

b、c曲线与a曲线对比, 最突出的差别是前者幅度低。由b、c曲线幅度基本一致可知这并非递推问题, 而是dB/dt与H_z的特性不同所致。

2.2 斜阶跃波

斜阶跃波dB/dt响应的改正法主要分为两大类:幅度改正法, 比如Fitterman法; 延时改正法(以往称为坐标移动法)。限于篇幅本文只讨论后者。

延时改正法计有t_k、t_h和t_a三种。前两种改正不足, 后一个改正过渡^[6]。

本文借鉴文献[5]的方法提出一项新的改正法— — 等效延时改正法。

2.2.1 等效延时改正法

2.2.1.1 全区视电阻线ρ _f计算

设递推H_z未做过延时改正。将斜阶跃波时段t_r分为M个阶跃波单元, 公式(6)、(7)改写为

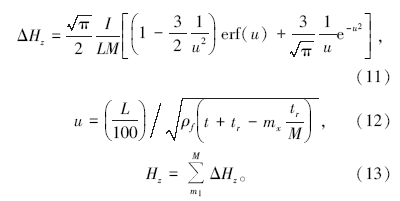
以上3式中:M为后沿t_r分割单元总数, m_x为M单元中某一分割单元。

在文献[5]中, m_x对应的延时是从分割单元的起始边算起, 本文则从分割单元的中间算起, 这样计时分割总数M较少, 精度已能满足要求。2种计时特点示于图11。图中a曲线ρ _f的误差在M=1时为37.1%、M=60为2.2%; b曲线的误差在M=1为2.6%, M=11误差低到0.06%。以下图件中的计算曲线皆取M=11。

	Figure Option View Download New Window
	图11 斜阶跃波1-D反演ρ _r与分割单元数M之关系曲线

2.2.1.2 等效延线t_e计算

上述求ρ _f的方法中各分割单元m_x距某计算延时道的时间不同, 显然所求得的ρ _f已不是对应原计算道的延时, 而是对应式(13)中隐函数“ t” 的延时。

将求得的ρ _f代入式(5)和式(7), 设后沿t_r=0, 改变t值以改变H_z, 逐渐逼近该延时递推的H_z。当逼近达到预定的精度时, 该时刻输入的“ t” 即相当隐函数“ t” , 本文称之为等效延时“ t_e” 。

此延时改正法的最大特点是先求ρ _f后求t_e, 而以前的延时改正法是先改正延时后求ρ _f。若延时改正不当则计算出的ρ _f也不当, 而与这两个参数有关的1-D反反演值ρ _r就会更差。

2.2.2 延时改正法效果对比

以往的3种延时改正法中, 原作者认为最好的是t_h(双曲线法)^[3], 故仅以它与t_e法作效果对比。所选H模型中的低阻层位于中— 近区, 这应是工作中的正常选择。由结果可见:t_e改正的d曲线与t_r=0的a曲线重合最好, t_h改正的c曲线则改正不足(图12A); 改正不足使H_z偏小, 从而对应延时的ρ _f偏高(图12B); ρ _r则急剧下降畸变, 而t_e改正的b曲线与a曲线(t_r=0)重合很好(图12C)。事物一分为二, 重合很好但是失去了早延时的信息。前已叙及, 式(11)为近似式, 它并未将斜阶跃波响应完全改为阶跃波响应, 故在早延时还有第一地层的一些信息, 为此计算绘制了曲线d。d曲线计算用的ρ _f与图12B中b曲线是同一值, 但延时t未改正。就d曲线特征而言它有参考意义, 为叙述方便称它为定性改正。

	Figure Option View Download New Window
	图12 后延效应改正效果

2.2.3 第一延时道(t₁)的选择

斜阶跃波与野外实际工作有关, 早延时数据受干扰很多, 比如地形起伏、电网的磁场干扰等, 故公式(2)不宜采用。以下讨论仅与公式(1)有关。

1) 前文已说明, 根据递推H_z的精度需要, t₁道的综合参数τ ₀≥ 0.015, 因此反推第一道为:

$\begin{matrix} t_{1} = \frac{6 L^{2}}{ρ_{f 1}} 10^{- 6}, (14) \end{matrix}$

式中:t₁为第一取样延时道(ms); L为发射回线边长(m); ρ ₁为第一层视电阻率, 可由dB/dt数据求得, 或由其他物探数据综合得出。

2)与t₁选择有关的参数还有接收探头本身的延时t_c(coil delay)。若所用仪器末提供此数据时可釆用

$\begin{matrix} t_{c} \approx 0.253 / \sqrt{f} (15) \end{matrix}$

计算。该式根据文献[3]中有关公式简化得出, 式中:t_c单位为ms, f为线圈谐振频率, 单位kHz。

3)试算分析。假设一个比较极端的情况:ρ ₁=9 Ω · m, L=300 m, 则t₁=0.06 ms; 对于t_c自然愈小愈好, 若t_c< t₁, 则第一延时即为t₁, 反之若t_c> t₁, 则第一延时选择t_c。以实用仪器为例。SIROTEM的线圈探头的谐振频率f=22 kHz, 相应t_c=0.054 ms; PEM系统的f=10 kHz, t_c=0.08 ms。正如上述情况, 前者第一延时选 0.06 ms, 后者选0.08 ms。

3 实例

精选3个实测成果与本文算法结果进行比较, 意在说明算法的实用效果, 而不是地质效果, 故地质情况叙述很少。

3.1 实例计算对比

3.1.1 磁通门探头正常场资料

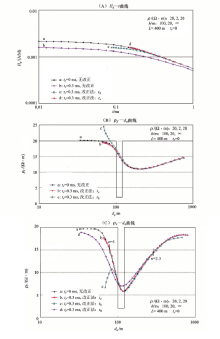
FG-SM-24磁通门探头在国外釆用较多, 目前已引进国内。某单位引进后在无矿地区试用, 图13为试用成果与本文算法结果之对比。

	Figure Option View Download New Window
	图13 FG-SM-24测试等对比曲线

图中a、c为ρ _f曲线, a为dB/dt数据计算, c为磁通门所测B_z数据计算, 两者都是由试用者计算; b曲线为dB/dt递推H_z计算之ρ _f曲线。由3种曲线的ρ _f与t_e计算出d、e、f这3条ρ _r 1-D反演曲线。ρ _f 3条曲线中b曲线位于a、c曲线之间, 虽然3条曲线特征基本一致, 但b曲线最圆滑。

3条ρ _f曲线的特征总体一致, 但d和f曲线误差太大, 唯有e曲线仍很圆滑。

3.1.2 高温超导SQUID磁强计导电异常资料

通榆山铜矿是20世纪90年代根据TEM异常布置钻孔验证发现的, ZK9301孔见矿七层, 第一层深约82 m, 最深一层约252 m, 总厚19.5 m。此后该地成为物探试验方法效果地区之一。

图14为2012年实测资料, 用Crone PEM系统观测接收线圈之信号dB/dt, 用SQUID磁强计观测信号B_z。曲线a、b为原观测者计算, c、d曲线为笔者计算。由图可见:SQUID的功率灵敏度最强, 故视深度最大; 4条1-D反演曲线的低阻异常特征一致, 但d曲线最圆滑。

	Figure Option View Download New Window
	图14 内蒙古通榆山铜矿LI0线ST1620点ρ _r— d_a曲线

3.1.3 线圈探头高阻异常资料

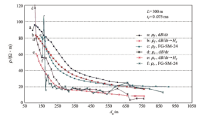
图15为2007年在内蒙古查干淖尔苏木用IGGETEM系统观测的资料。图中dB/dt数据的1-D反演ρ _r曲线a为观测者计算, 其余为笔者用本文方法计算。b曲线的数据经等效延时t_e改正, c曲线则是经t₀“ 定性改正” , d曲线是用公式(10)计算的1-D反演ρ _e。由H_z计算的ρ _r异常幅度都低于dB/dt计算的ρ _r异常幅度, 利用经验反演公式(10)计算的d曲线异常幅度较强, 接近a曲线。

	Figure Option View Download New Window
	图15 内蒙古某地c25线27测点电阻率1-D反演曲线

3.2 对比结果要点

所选3个实例中, 2台系国外知名的GDP-14和CRONE PEM系统观测, 另一台为应用较广的国产IGGETEM系统观测, 探头也涉及3种, 地质— 地球物理特性也涉及3种, 可谓实例不多, 代表性甚广。

这些数据计算的曲线特征基本一致, 但递推H_z计算之曲线最圆滑, 因为递推的过程具有滤波偶然误差的作用。这是优点又有不足之处, 它会使弱响应不明显甚至消失。图15中, d_a≈ 500 m处a曲线高阻线段变圆滑而消失, 原因可能在此。

H_z计算之ρ _r异常幅度普遍较dB/dt计算的低, 这不是递推的结果, 而是H_z与dB/dt衰减特性的必然情况。为弥补此不足, 釆用了经验反演式(公式10), 实例证明有效。

4 结论与建议

1) 本算法以理论为基础, 结合实际经验, 应用独特思路, 解决了以往递推H_z的难点以及dB/dt响应计算全区视电阻率的固有问题, 提出了适用的视深度经验改正法及等效延时改正法, 大量模型计算及实例证明这是一套有效、实用的方法。

2) 本方法适用的区带与应用电动势响应相同, 即中区及近区。H_z由dB/dt递推得出, 故只要dB/dt工作设计正确、数据可靠, 则H_z数据也同样可靠。

3) 本算法亦有弱项。1-D反演ρ _r值偏低, 外加递推H_z具有滤波性质, 低幅度的异常可能被忽视。

4) 本算法建立在dB/dt数据上且有弱项, 故建议本算法与求解dB/dt的算法并用, 提高解释水平, 而不是要取代它。

感谢:本文在研究编写过程中得到张杰、王兴春两位高级工程师的帮助, 提供了资料、观点和建议, 在此表示感谢。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Levy G M. Correction of measured transient electromagnetic response for finite transmitter turn-off Duration[J]. Technical Note TN-16, Geonics Ltd, 1984. [本文引用:1]
[2]	Spies B R, Eggers D E. The use and misuse of apparent resistivity in electromagnetic methods[J]. Geophysics, 51(7). [本文引用:1]
[3]	蒋邦远. 实用近区磁源瞬变电磁法勘探[M]. 北京: 地质出版社, 1998. [本文引用:2]
[4]	蒋邦远. 磁源TEM测深一维反演经验式及应用效果[J]. 物探与化探, 2000, 29(2): 99-104. [本文引用:1]
[5]	白登海. 瞬变电磁法中两种关断电流对响应函数的影响及其应对策略[J]. 地震地质, 2001, 23(2): 245-251. [本文引用:1]
[6]	杨云见, 王绪本, 何展翔. 瞬变电磁法中的斜阶跃波效应及常规的几种校正方法分析[J]. 物探化探计算技术, 2006, 28(2): 129-132. [本文引用:1]
[7]	陈明生, 田小波. 电隅源瞬变电磁测深研究(五)——实测感应电压转换成垂直磁场[J]. 煤田地质与勘探, 1999, 27(5): 63-64. [本文引用:1]
[8]	罗国平, 魏凤英. 瞬变电磁法磁场及视电阻率研究[J]. 中国煤田地质, 2000, 12(2): 60-62. [本文引用:1]