瞬变电磁法低阻薄层反演

引用本文

郭睿, 武欣, 肖攀, 方广有. 瞬变电磁法低阻薄层反演[J]. 物探与化探, 2017,41(4): 753-757.
GUO Rui, WU Xin, XIAO Pan, FANG Guang-You. Transient electromagnetic inversion for thin layer with low resistivity[J]. Geophysical and Geochemical Exploration, 2017,41(4): 753-757.
Doi:10.11720/wtyht.2017.4.27 复制到剪切板

Permissions

《物探与化探》编辑部

瞬变电磁法低阻薄层反演

郭睿^1,², 武欣¹, 肖攀^1,², 方广有¹

1.中国科学院电子学研究所电磁辐射与探测技术重点实验室,北京 100190

2.中国科学院大学电子电气与通信工程学院,北京 100049

作者简介: 郭睿(1993-),男,中国科学院电子学研究所电磁场与微波技术专业在读研究生(硕士),研究方向为瞬变电磁法正反演研究。

收稿日期: 2017-01-16

基金: 国家重大科研装备研制项目“深部资源探测核心装备研发”(ZDYZ2012-1)

摘要

瞬变电磁反演方法对瞬变电磁数据解释有极其重要的作用。在实际工程中,由于地下低阻薄层响应较弱,现有的反演方法很难将其分辨出来。文中基于正则化反演理论,提出了一种新的模型约束加权方法,对地层的光滑度施加了周期性大幅变化的权值,通过两次迭代可自适应的反演出低阻薄层区。小权值使模型对电性参数的大尺度变化有较高的敏感性,便于筛选出异常薄层;同时,与小权值交错分布的大权值能尽量保证反演曲线的连续性,降低反演的多解性。通过仿真验证,该方法对低阻薄层区的分辨能力比传统算法更高,对较厚区域低阻区的分辨能力与传统方法类似。该方法迭代稳定,不依赖地层先验信息,具有很高的工程实践性。

关键词: 瞬变电磁; 反演; 正则化; 加权; 低阻薄层

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2017)04-0753-05

Transient electromagnetic inversion for thin layer with low resistivity

GUO Rui^1,², WU Xin¹, XIAO Pan^1,², FANG Guang-You¹

1. Key Laboratory of Electromagnetic Radiation and Sensing Technology, Chinese Academy of Sciences, Beijing 100190, China

2. School of Electronic, Electrical and Communicating Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

Inversion is an important tool for transient electromagnetic data interpretation. This paper proposes a novel weighing scheme with periodic vibration for roughness restriction based on the regularized optimization theory. The small weights make the models sensitive to reflecting parameters' great changes and thus it is easy to show the thin layer with low resistivity. The large weights distributed near small weights can make sure the continuity of the inversion results, which reduces the variety of the solution. Synthetic models show that this method has higher resolution for low resistivity thin layer than traditional ones and keeps the same resolution with traditional ones when inverting low resistivity large areas. In addition, this method converges stably and does not rely on a prior information about the ground structure, thus making sure its application in practice.

Keyword: transient electromagnetic method; inversion; regularization; weight; thin layer with low resistivity

Show Figures

0 引言

瞬变电磁法(TEM)是地球物理勘察手段的重要组成部分^[1], 已被广泛应用于矿产资源勘探、水文调查、未爆物探测等领域 $\begin{matrix} ^{[24]} \end{matrix}$ 。瞬变电磁系统使用长接地导线源或回线源发射脉冲电流, 根据电磁感应定律, 大地内部会激励形成涡旋电流并持续衰减, 进而感应出二次场。通过处理二次磁场数据, 实现对地下目标的探测 $\begin{matrix} ^{[56]} \end{matrix}$ 。

薄层地质体的有效探测是地球物理探测中重要且困难的问题^[7]。由于电磁场在高阻中衰减很小, 瞬变电磁探测具有高阻屏蔽弱、垂向分辨率高的优点, 可以有效探查到地下低阻区。对于瞬变电磁法的低阻薄层探测, 许多学者已进行了有效的探索:牛之琏^[8]讨论了瞬变电磁法对导电层的探测能力; 薛国强^[7]对有无薄层存在时的层状大地视电阻率曲线进行了对比, 通过二者的相对误差分析了瞬变电磁法对薄层结构体的分辨能力; 王战军^[9]给出不同层电阻率差异比时瞬变电磁对低阻薄层的探测极限; 陈卫营^[10]探讨了电性源瞬变电磁对薄层的探测能力; Li Xiu^[11]在视电阻率成像的基础上引入自适应收缩性遗传算法, 提高了瞬变电磁法对地下薄层的分辨能力。以上研究基于层状大地的正演响应曲线或视电阻率曲线对低阻薄层的探测能力进行分析, 对指导瞬变电磁低阻薄层探测发挥了重要作用。

相较于视电阻率成像, 反演能对观测数据进行更严格的数学拟合, 得到的结果更真实可靠。目前反演技术采用的目标函数普遍基于正则化理论^[12], 其中Occam反演 $\begin{matrix} ^{[1314]} \end{matrix}$ 已被广泛应用于工程实践中 $\begin{matrix} ^{[1517]} \end{matrix}$ 。本文基于Occam反演理论, 提出了一种新的模型约束加权方法, 该算法对模型参数变化有更高的灵敏度, 能很好地凸显低阻薄层结构特征。

1 模型约束加权反演

1.1 反演目标函数

对于一维层状大地模型, 理论响应d可通过正演函数F(· )求得

$\begin{matrix} d = F (m), (1) \end{matrix}$

式中m为待反演模型参数(包括各层的电阻率和深度)。若观测响应值为d_obs, 则理论响应与观测值之间的不匹配程度可表示为

$\begin{matrix} P_{1} = ‖ W_{d} (d - d_{obs}) ‖_{2}^{2}, (2) \end{matrix}$

式中:W_d为数据的权值矩阵, ‖ …‖ ²为定义在数据空间上的二范数。若共有L条时间测道, 各时间测道误差为σ _i, 则d=[d₁, d₂, …, d_L]^T, W_d=diag(σ ₁, σ ₂, …, σ _L)。将大地纵向剖分N层, 第i层厚度为h_i且h_i/h_i+₁< 1, 电阻率为ρ _i, 并假设各层电阻率变化尽量平缓, 可将各层电阻率约束用如下公式表达

$\begin{matrix} P_{2} = ‖ C \partial ρ ‖^{2}, (3) \end{matrix}$

式中C为修正各层间平滑约束强度的加权矩阵。

根据正则化理论, 将P₁、P₂构成无约束的反演目标函数, 并用参数λ 描述模型约束强度, 可得

$\begin{matrix} \begin{matrix} P & = P_{1} + λ P_{2} \\ = ‖ W_{d} (d - d_{obs}) ‖_{2}^{2} + λ ‖ C \partial ρ ‖^{2} 。 (4) \end{matrix} \end{matrix}$

1.2 模型约束加权法

对于传统正则化反演, 普遍默认C为单位对角阵, 当存在较强先验信息时, 可修改C使其对特定深度的电阻率产生约束。然而, 在实际工程中先验信息较难获取, 不正确的先验信息会加剧反演结果的不准确性。

低阻薄层反演的本质是在较小的电阻率网格范围内使电阻率产生较大的变化, 即使该层的平滑约束权值较小。在无法提供低阻薄层先验深度的情况下, 可将平滑约束强度加权矩阵按照如下方法设置:

$\begin{matrix} \begin{matrix} C_{1} (x) = diag (\sqrt{1 - α | \cos (βx) |}), (5) \\ C_{2} (x) = diag (\sqrt{1 - α | \sin (βx) |}), (6) \end{matrix} \end{matrix}$

式中α 、β 为调节权值相对大小的系数, 且α < 1。

当反演低阻薄层时, 需采用较密的纵向网格剖分, 对上述函数在各层号处离散采样, 并选择较大的α 、β 值。图1为C的权值分配示意。

	Figure Option View Download New Window
	图1 模型约束加权矩阵的权值分配示意

若低阻薄层深度落在C中权系数较大区间, 其电阻率光滑程度较强, 即无法反演出低阻薄层的特征。然而, 当分别取C₁、C₂进行反演时, 电阻率突变区间总可以被较小系数的权重覆盖(图1), 若低阻薄层存在, 至少存在一个反演结果, 能够体现低阻薄层区域; 若低阻薄层不存在, 即使权重较小会导致反演电阻率出现微小震荡, 但不会改变电阻率变化整体趋势, 二者反演结果会近似吻合。参数α 、β 可将先验低阻薄层信息加入反演方程中, 加速收敛, 提高结果可靠性。

1.3 最优化迭代算法

将正演函数线性化, 可将模型ρ ₁处的正演响应近似表示为

$\begin{matrix} F (ρ_{1}) = F (ρ_{0}) + G_{0} (ρ_{1} - ρ_{0}), (7) \end{matrix}$

式中G₀为正演函数在模型ρ ₀处的偏导数矩阵, 其元素为

$\begin{matrix} G_{0 ij} = \frac{\partial F_{i} (ρ_{0})}{\partial ρ_{j}} 。 (8) \end{matrix}$

将目标函数写为

$\begin{matrix} \begin{matrix} P = ‖ W_{d} (F (ρ_{0}) + G_{0} ρ_{1} - G_{0} ρ_{0} - d_{obs} ‖_{2}^{2} \\ + λ ‖ C \partial ρ ‖^{2} (9) \end{matrix} \end{matrix}$

其中

$\begin{matrix} \partial = {[\begin{matrix} 0 & 0 \\ - 1 & 1 \\ - 1 & 1 & 0 \\ \dots \\ 0 & - 1 & 1 \end{matrix}]}_{N \times N} (10) \end{matrix}$

令

得

$\begin{matrix} \begin{matrix} ρ_{1} = [(W_{d} G_{0})^{T} (W_{d} G_{0}) + α \partial^{T} C^{T} {C \partial]}^{- 1} \cdot \\ W_{d} [d_{obs} + G_{0} ρ_{0} - F (ρ_{0})] 。 (12) \end{matrix} \end{matrix}$

得到电阻率ρ ₁之后, 计算当前拟合差

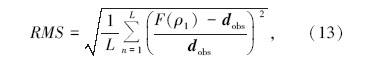
若拟合差小于期望值, 计算终止; 否则将新产生的ρ ₁作为下次迭代的初始模型ρ ₀重复上述步骤, 直到RMS小于期望值或达到最大迭代次数, 迭代终止。分别计算C₁、C₂的反演值, 若二者结果相差不大, 则说明无低阻薄层存在, 二者之一可作为反演结果; 若其中之一反演曲线出现低阻薄层, 选择此时结果作为最终反演结果。

2 仿真验证

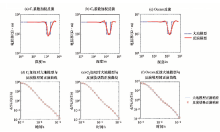
为验证算法有效性, 对大回线地面瞬变电磁系统的理论数据进行了反演测试。发射线框边长100 m, 共4匝, 发射电流为5 A, 接收线圈放置在发射线框中心处。假设五层大地模型, 厚度分别为150、40、50、100 m, 半空间, 电阻率分别为400、100、200、30、200 Ω · m(模型1)。本文提出的低阻薄层反演算法结果如图2所示。

	Figure Option View Download New Window
	图2 模型1不同反演方法的反演结果及其正演曲线

3种反演模型均能产生相近的正演响应, 但当不采用模型约束加权时, 无法体现出深度150 m、厚度为40 m的低阻薄层; 采用C₁、C₂加权分别反演时, C₁中低阻薄层深度处权值较小, 可以实现电阻率较大变化, C₂中低阻薄层深度处加权较大, 无法体现电阻率突变特性, 其在低阻薄层处的加权效果同Occam反演。综合C₁、C₂加权, 选择前者作为反演结果。

若发射、接收条件不变, 将大地模型设置为厚度分别为180、60、60、100 m, 半空间, 每层电阻率不变(模型2), 低阻薄层反演算法与Occam反演对比如图3所示。该大地模型使低阻薄层区落入C₂权值较小处, C₁、C₂反演结果反转, 此时可选后者作为反演结果。

若发射、接收条件不变, 假设地下有一较厚的低阻区, 厚度为100 m, 半空间, 电阻率为400、100、400 Ω · m(模型3), 低阻薄层反演算法与Occam反演对比如图4所示。可以看到C₁、C₂两种反演均能体现100 m低阻区, 但形态稍有差异; 从理论模型与反演模型的正演响应来看, 二者的拟合程度都达到较高水平。图4a和f所示的Occam反演此时能反映出该低阻区。三者反演模型均可作为最终的反演结果。

	Figure Option View Download New Window
	图3 模型2不同反演方法的反演结果及其正演曲线

	Figure Option View Download New Window
	图4 模型3不同反演方法的反演结果及其正演曲线

3 结论

本次研究的目的标主要为提高瞬变电磁法低阻薄层反演的分辨率, 使用的主要方法为对大地进行固定厚度的层状剖分, 并利用正则化方法进行电阻率反演。

文中提出了一种模型约束加权方法:通过正余弦函数对模型约束方程进行修正, 使反演曲线在保证连续性的前提下提高对电阻率变化的敏感性。本方法摆脱了采用固定权值加权矩阵对先验信息的依赖, 通过2次一维反演即可自适应地完成有无低阻薄层区及其深度和电阻率的判定。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Nabighian M N. Electromagnetic methods in applied geophysics[M]. Tulsa, USA: SEG Books, 1988. [本文引用:1]
[2]	Smith R, Fountain D, Allard M. The MEGATEM fixed-wing transient EM system applied to mineral exploration: A discovery case history[J]. First Break, 2003, 21(7): 73-77. [本文引用:1]
[3]	He Z, Zhao Z, Liu H, et al. TFEM for oil detection: Case studies[J]. Leading Edge, 2012, 31(5): 518-521. [本文引用:1]
[4]	Pasion L R, Oldenburg D W. A discrimination algorithm for UXO using time domain electromagnetics[J]. Journal of Environmental and Engineering Geophysics, 2001, 6(2): 91-102. [本文引用:1]
[5]	翁爱华, 刘云鹤, 陈玉玲, 等. 矩形大定源层状模型瞬变电磁响应计算[J]. 地球物理学报, 2010, 53(3): 646-650. [本文引用:1]
[6]	武欣, 薛国强, 陈卫营, 等. 瞬变电磁探测系统 (CASTEM) 试验对比——安徽颖上大王庄铁矿[J]. 地球物理学报, 2016, 59(12): 4448-4456. [本文引用:1]
[7]	薛国强, 邓湘. 瞬变电磁法对薄层的探测能力[J]. 石油地球物理勘探, 2007, 42(6): 709-713. [本文引用:2]
[8]	牛之琏. 瞬变电磁测深法对导电层的探测能力[J]. 地质与勘探, 1992, 28(1): 42-47. [本文引用:1]
[9]	王战军, 朱自强, 李建慧, 等. 瞬变电磁法对低阻薄层的分辨能力研究[J]. 物探化探计算技术, 2012, 34(6): 646-651. [本文引用:1]
[10]	陈卫营, 薛国强. 电性源瞬变电磁对薄层的探测能力[J]. 物探与化探, 2015, 39(4): 775-779. [本文引用:1]
[11]	Li X, Xue G Q, Song J P, et al. Application of the adaptive shrinkage genetic algorithm in the feasible region to TEM conductive thin layer inversion[J]. Applied Geophysics, 2005, 2(4): 204-210. [本文引用:1]
[12]	Tihonov A N. On the regularization of ill-posed problems[J]. European Economic Review, 1996, 41(6): 1111-1146. [本文引用:1]
[13]	Constable S C, Parker R L, Constable C G. Occam's inversion: A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. [本文引用:1]
[14]	deGroot-Hedlin C, Constable S. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data[J]. Geophysics, 1990, 55(12): 1613-1624. [本文引用:1]
[15]	Vallée M A, Smith R S. Application of Occam's inversion to airborne time-domain electromagnetics[J]. The leading edge, 2009, 28(3): 284-287. [本文引用:1]
[16]	强建科, 李永兴, 龙剑波. 航空瞬变电磁数据一维 Occam 反演[J]. 物探化探计算技术, 2013, 35(5): 501-505. [本文引用:1]
[17]	Guo R, Wu X, Rao L T, et al. Sharp boundary based transient electromagnetic inversion[C]//Proceedings of 7th International Conference on Environmental and Engineering Geophysics & Summit Forum of Chinese Academy of Engineering on Engineering Science and Technology. Kuala Lumpur: Atlantis Press, 2016. [本文引用:1]

1988

0.0

... 0 引言瞬变电磁法(TEM)是地球物理勘察手段的重要组成部分^[1],已被广泛应用于矿产资源勘探、水文调查、未爆物探测等领域 24 ...

2003

0.0

2012

0.0

2001

0.0

2010

0.0

2016

0.0

2007

0.0

... 薄层地质体的有效探测是地球物理探测中重要且困难的问题^[7] ...

... 薛国强^[7]对有无薄层存在时的层状大地视电阻率曲线进行了对比,通过二者的相对误差分析了瞬变电磁法对薄层结构体的分辨能力 ...

1992

0.0

... 对于瞬变电磁法的低阻薄层探测,许多学者已进行了有效的探索:牛之琏^[8]讨论了瞬变电磁法对导电层的探测能力 ...

2012

0.0

... 王战军^[9]给出不同层电阻率差异比时瞬变电磁对低阻薄层的探测极限 ...

2015

0.0

... 陈卫营^[10]探讨了电性源瞬变电磁对薄层的探测能力 ...

2005

0.0

... Li Xiu^[11]在视电阻率成像的基础上引入自适应收缩性遗传算法,提高了瞬变电磁法对地下薄层的分辨能力 ...

1996

0.0

... 目前反演技术采用的目标函数普遍基于正则化理论^[12],其中Occam反演 1314已被广泛应用于工程实践中 1517 ...

1987

0.0

1990

0.0

2009

0.0

2013

0.0

2016

0.0