重力梯度测量对加速度计温度系数的需求分析

引用本文

孙洁洁, 李海兵, 丁祝顺. 重力梯度测量对加速度计温度系数的需求分析[J]. 物探与化探, 2017,41(4): 736-740.
SUN Jie-Jie, LI Hai-Bing, DING Zhu-Shun. Requirement analysis of accelerometer temperature coefficient in gradiometer measurement[J]. Geophysical and Geochemical Exploration, 2017,41(4): 736-740.
Doi:10.11720/wtyht.2017.4.24 复制到剪切板

Permissions

《物探与化探》编辑部

重力梯度测量对加速度计温度系数的需求分析

孙洁洁, 李海兵, 丁祝顺

北京航天控制仪器研究所,北京 100039

作者简介: 孙洁洁(1990-),男,工学硕士,中国运载火箭技术研究院,研究方向:热分析。

收稿日期: 2017-01-13

基金: 国家国际科技合作专项(2014DFR80750)航天科技集团公司九院创新基金项目

摘要

加速度计的零位偏置、标度系数对温度很敏感,从而影响重力梯度测量系统的精度,将加速度计零位偏置、标度系数的温度系数代入重力梯度测量方程中,并给定重力梯度测量系统的精度、测量范围和温度变化范围,经过仿真计算得到系统对加速度计温度系数的要求。最后,选取某典型加速度计,通过优化组合,温度系数两正、两负配对使用,使得4只加速度计标度系数的温度系数和从15.255 ppm/℃降低到1.075 ppm/℃,满足系统要求。

关键词: 重力梯度测量; 石英挠性加速度计; 温度系数; 需求分析

中图分类号:P312.1/O551.2 文献标志码:A 文章编号:1000-8918(2017)04-0736-05

Requirement analysis of accelerometer temperature coefficient in gradiometer measurement

SUN Jie-Jie, LI Hai-Bing, DING Zhu-Shun

Beijing Institute of Aerospace Control Devices,Beijing 100039,China

Abstract

The accelerometer bias and the scale factor are sensitively influenced by temperature so that the precision of gradiometer measurement system is affected. The measurement equation is derived according to the principle of gravity gradiometer including the temperature coefficient of accelerometer bias and the scale factor. The values' range of scale factor coefficient of temperature is presented by assuming some parameters and analyzing the relation equation. Taking some accelerometers for example, the choice of two positive temperature coefficients and two negative temperature coefficients makes the total temperature coefficient fall from 15.255 ppm/℃ to 1.075 ppm/℃ and meets the demand of the temperature coefficient.

Keyword: gradiometer measurement; quartz flexible accelerometer; temperature coefficient; requirement analysis

Show Figures

0 引言

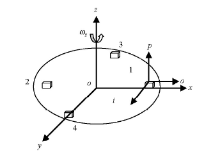
重力场信息在资源勘探、国土资源调查和地球科学研究等领域具有重大作用, 重力梯度测量可以测得更加精细的重力场信息, 因此, 重力梯度测量成为国内外研究的重点 $\begin{matrix} ^{[13]} \end{matrix}$ 。目前, 国外实际投入使用的重力梯度测量系统是旋转加速度计重力梯度仪^{[4, 5]}, 我国重力梯度仪研制起步较晚, 面临的问题还较多, 旋转加速度计重力梯度仪还处于原理样机阶段。加速度计作为旋转式重力梯度仪的核心部件, 其受温度的影响较大, 是制约重力梯度仪测量精度提高的关键因素。而高精度的温度控制系统很难实现, 因此需要对加速度计进行热分析、热设计并进行温度补偿 $\begin{matrix} ^{[615]} \end{matrix}$ , 研究加速度计温度系数与重力梯度测量系统的影响关系式, 可以明确加速度计各项指标要求, 减少温度对系统的影响, 从而提高系统测量精度。

1 理论基础

旋转加速度计重力梯度仪是采用4只或8只高精度加速度计对称分布在旋转圆盘上如下图1所示, 加速度计检测得到重力梯度信号, 将信号输入到微弱信号检测电路与同步信号电路中, 经处理得到重力梯度值。整个过程中受温度影响最大的是前端加速度计的检测过程。因此, 笔者分析了重力梯度系统与加速度计温度系数之间的相互影响关系。

	Figure Option View Download New Window
	图1 旋转加速度计重力梯度仪测量原理

利用牛顿第二运动定律可得圆盘上的加速度计检测质量中心感受到的加速度为^{[6, 7, 8]}:

$\begin{matrix} \begin{matrix} f_{i} = a_{i} = a_{i} \cdot τ_{i}^{o} = (a_{o} + R \dot{ω} \times r_{i}^{o} + \\ R ω_{e} \times (ω_{e} \times r_{i}^{o}) + Rω \times (ω \times r_{i}^{o}) - \\ g_{o} - Γ \cdot r_{i}) \cdot τ_{i}^{o}, (1) \end{matrix} \end{matrix}$

其中:a_i为加速度计输出轴上的加速度, 地球惯性坐标系为x_iy_iz_i, 转盘坐标系为上图所示xyz, 且转盘坐标系与惯性坐标系对齐, 坐标原点o位于圆盘圆心, x与x_i对齐, y与y_i对齐, z与z_i对齐, 加速度计坐标系为上图所示oip, 坐标原点位于加速度计检测质量中心; a_o=[a_ox a_oy a_oz]^T为转盘中心的线加速度在转盘坐标系中的分解; g_o=[g_ox g_oy g_oz]^T为重力加速度在转盘坐标系中的分解; ω =[ω _x ω _y ω _z]^T为转盘的角速度在转盘坐标系中的分解, ω _z为转盘转动的恒定转速; ω _e=[ω _ex ω _ey ω _ez]^T为地球转动角速度在地球惯性坐标系中的分解; $\begin{matrix} \dot{ω} \end{matrix}$ =[ $\begin{matrix} {\dot{ω}}_{x} \end{matrix}$ $\begin{matrix} {\dot{ω}}_{y} \end{matrix}$ $\begin{matrix} {\dot{ω}}_{z} \end{matrix}$ ]^T为转盘的角加速度在转盘坐标系中的分解; Γ = $\begin{matrix} [\begin{matrix} Γ_{xx} & Γ_{xy} & Γ_{xz} \\ Γ_{yx} & Γ_{yy} & Γ_{yz} \\ Γ_{zx} & Γ_{zy} & Γ_{zz} \end{matrix}] \end{matrix}$ 为圆盘中心的重力梯度张量, 且Γ _yx=Γ _xy, Γ _zx=Γ _xz, Γ _yz=Γ _zy; r_i为第i个加速度计检测质量中心到圆盘中心的矢径; $\begin{matrix} r_{i}^{O} \end{matrix}$ 为矢径的单位方向向量; $\begin{matrix} τ_{i}^{O} \end{matrix}$ 为矢径的单位切向向量。

工程应用中, 加速度计的输入输出数学模型一般只考虑零位偏置、标度系数, 其公式为^[15],

$\begin{matrix} V = K_{1} (K_{o} + a_{i}), (2) \end{matrix}$

其中:V为加速度计输出电压, K₀为加速度计零偏, 石英挠性加速度计的标度系数K₁可近似地用下式表示^[18]:

$\begin{matrix} K_{1} \approx \frac{K_{B}}{K_{t}}, (3) \end{matrix}$

其中:K_B为摆性, K_B=mL, m为摆组件质量, L为摆组件质心到挠性支承中心的距离; K_t为力矩器刻度因数, K_t=2NlL_tB_δ, N为单个力矩器线圈匝数, l为每匝线圈长度, L_t为力矩器线圈安培力作用点到输出轴的垂直距离, B_δ为工作气隙磁通密度。

在常温下, Κ ₁对温度Τ 的导数为^[18]:

$\begin{matrix} \begin{matrix} \frac{d K_{1}}{dT} = - \frac{K_{B}}{K_{t}} (β_{l} + β_{δ}) = - K_{1} (β_{l} + β_{δ}), (4) \\ α_{K_{1}} = \frac{- K_{1} (β_{l} + β_{δ})}{K_{1}} = - (β_{l} + β_{δ}), (5) \end{matrix} \end{matrix}$

其中: $\begin{matrix} α_{K_{1}} \end{matrix}$ 为标度系数的温度系数; β _l为动圈导线的线胀系数; β _δ为工作气隙磁感应温度系数。

根据式(5)可知, 加速度计标度系数的温度系数与线圈的线胀系数、力矩器磁钢温度系数有关, 其中无磁性漆包线β _l=1.67× 10^-⁵/K, β _δ为工作气隙磁感应温度系数, 从磁性材料手册查到部分永磁合金属性如下表1所示, 由表格中的数值可以看到磁感应温度系数较大, 最小的温度系数也比导线的线胀系数高一个数量级, 且都为负的温度系数, 一般通过磁补偿的方式对温度系数进行补偿^[7]。

表1 永磁合金温度系数^[19]

2 加速度计温度系数对重力梯度测量的影响

仅考虑加速度计标度系数K₁和零位偏置K_o受温度的影响, 得到加速度计的输出模型为:

$\begin{matrix} V_{t} = K_{1} (t) (K_{o} (t) + a_{i}), (6) \end{matrix}$

其中:t为温度, 单位℃; K₁(t), K_o(t)为在t温度时标度系数和零位偏置。

将式(6)代入重力梯度测量方程, 得到下式:

$\begin{matrix} \begin{matrix} V_{1 t} + V_{2 t} - V_{3 t} - V_{4 t} = K_{11} (t) (K_{10} (t) + a_{n 1}) + \\ K_{21} (t) (K_{20} (t) + a_{n 2}) - K_{31} (t) (K_{30} (t) + a_{n 3}) - \\ K_{41} (t) (K_{40} (t) + a_{n 4}) (7) \end{matrix} \end{matrix}$

其中:a_ni(i=1, 2, 3, 4)为加速度计i的输出值。从重力梯度测量方程中提取含有2倍频的项, 有以下两项:

$\begin{matrix} \begin{matrix} V_{2 f} = R (K_{11} (t) + K_{21} (t) + K_{31} (t) + K_{41} (t)) (Γ_{xy} - ω_{ex} ω_{ey} - ω_{x} ω_{y}) \\ W_{2 f} = - \frac{1}{2} R (K_{11} (t) + K_{21} (t) + K_{31} (t) + K_{41} (t)) (Γ_{xx} - Γ_{yy} - ω_{ex}^{2} + ω_{ey}^{2} - ω_{x}^{2} + ω_{y}^{2}) \end{matrix} (8) \end{matrix}$

其中:V₂_f, W₂_f为2倍频输出电压项。从式(8)可以得到加速度计的标度系数在输出结果的2倍频上, 对测量结果造成直接影响。为方便计算, 将小量ω _ex, ω _ey, ω _x, ω _y忽略, 将标度系数受温度影响式表示成:K₁(t)=K₁+Δ K₁, 只考虑加速度计的标度系数受温度变化的影响项:Δ K₁= $\begin{matrix} α_{K_{1}} \end{matrix}$ K₁Δ t, 代入式(8)可得,

$\begin{matrix} \begin{matrix} V_{2 f} = ΔtR Γ_{xy} (α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}), \\ {V^{'}}_{2 f} = - \frac{1}{2} ΔtR (Γ_{xx} - Γ_{yy}) (α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + \\ α_{K_{31}} K_{31} + α_{K_{41}} K_{41}) 。 \end{matrix} \end{matrix}$

考虑加速度计温度差为Δ t℃, 重力梯度测量误差项≤ n Eu(1 Eu=10^-⁹/s²), 与理想情况下重力梯度测量方程式比较, 可以得到:

$\begin{matrix} \begin{matrix} ΔtR Γ_{xy} (α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}) \leq 4 nR K_{1} \\ \frac{1}{2} ΔtR (Γ_{xx} - Γ_{yy}) (α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}) \leq 2 nR K_{1} \end{matrix} (9) \end{matrix}$

将式(9)转化为标度系数的温度系数的关系式为:

$\begin{matrix} \begin{matrix} \frac{α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}}{4 K_{1}} \leq \frac{n}{Δt Γ_{xy}} \\ \frac{α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}}{4 K_{1}} \leq \frac{n}{Δt (Γ_{xx} - Γ_{yy})} \end{matrix} (10) \end{matrix}$

从上式(10)中可以看到加速度计标度系数的温度系数与重力梯度测量系统的量程、测量精度有关, 精度要求越高, 温度系数要求越小; 温度差越大, 温度系数要求越小。给定设计指标要求, 则可以确定加速度计的性能要求; 同理, 若已知加速度计的性能参数, 可以求得重力梯度测量的精度和量程。

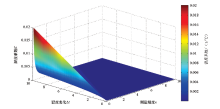
令Γ _xx± Γ _yy≤ 5 000 Eu, Γ _xy± Γ _yx≤ 400 Eu, Γ _xz± Γ _yz≤ 500 Eu, Δ t=0.1℃~10℃, 最小误差n=0.1~10 Eu, 重力梯度测量值取最大值Γ _xx-Γ _yy=5 000 Eu, Γ _xy=400 Eu, 代入式(10)中, 经三维绘图如图2所示。

	Figure Option View Download New Window
	图2 加速度计标度系数的温度系数范围

由上图2可以看出, 随着温度差的增大, 测量精度要求的提高, 4只加速度计温度系数之和与标度系数的比值越小, 即对加速度计的性能要求越高, 具体范围为:

$\begin{matrix} \begin{matrix} 2 \times 10^{- 6} & \leq \frac{α_{K_{11}} K_{11} + α_{K_{21}} K_{21} + α_{K_{31}} K_{31} + α_{K_{41}} K_{41}}{4 K_{1}} \\ \leq 0.02 (11) \end{matrix} \end{matrix}$

从上式(11)可以看到, 当重力梯度测量方程的测量精度n=0.1 Eu, Δ t=10℃, 要求加速度计标度系数的温度系数的小于2× 10^-⁶, 与典型加速度计温度系数相比要小一个数量级。如果四只加速度计的标度系数一致性较高, 则取K₁₁=K₂₁=K₃₁=K₄₁=K₁, 上式(11)可以转化为,

$\begin{matrix} 2 \times 10^{- 6} \leq \frac{α_{K_{11}} + α_{K_{21}} + α_{K_{31}} + α_{K_{41}}}{4} \leq 0.02 (12) \end{matrix}$

以铝镍钴合金为例进行计算说明, 其工作气隙磁感应温度系数为β _δ=-2× 10^-⁴/K, 补偿后温度系数为 $\begin{matrix} {β^{'}}_{δ} \end{matrix}$ =a× 10^-⁴+b× 10^-⁵, 则加速度计1标度系数的温度系数为,

$\begin{matrix} \begin{matrix} α_{K_{11}} & = - (β_{l} + {β^{'}}_{δ}) \\ = - (1.67 \times 10^{- 5} + a_{1} \times 10^{- 4} + b_{1} \times 10^{- 5}) 。 \\ (13) \end{matrix} \end{matrix}$

为了满足重力梯度测量系统对温度系数的要求, 将上式(13)代入式(12)中可以得,

$\begin{matrix} \begin{matrix} (a_{1} + a_{2} + a_{3} + a_{4}) \times 10 + \\ (b_{1} + b_{2} + b_{3} + b_{4}) > - 7.48 (14) \end{matrix} \end{matrix}$

上式中只要a₁+a₂+a₃+a₄=0, b₁+b₂+b₁+b₂> -7.48即可满足式(12)的要求, 通过此方法, 则不必将温度系数减小到10^-⁶数量级, 只需要保证10^-⁶项之前项数值相等, 符号相反即可, 这样经过相加补偿则可以得到很小的温度系数, 在满足重力梯度测量系统的精度要求下, 忽略标度系数受温度系数的影响。

3 温度系数匹配验证

以某批加速度计为例进行典型计算, 表2给出了加速度计的相关参数。

表 2 某型加速度计的参数

编号	K₁(mA/g)	$\begin{matrix} α_{K_{1}} \end{matrix}$ (ppm/℃)
1	1.323617	38.3
2	1.323792	-15.3
3	1.323684	21.4
4	1.323713	16.5
5	1.323747	-18.3

表 2 某型加速度计的参数

将表格中编号1~4的加速度计数值代入式(11), 可以求得:

$\begin{matrix} \frac{K_{11} α_{K_{11}} + K_{21} α_{K_{21}} + K_{31} α_{K_{31}} + K_{41} α_{K_{41}}}{K_{11} + K_{21} + K_{31} + K_{41}} = 15.224 ppm / ℃ (15) \end{matrix}$

上表2中加速度计的标度系数一致性较好, 优于10^-4, 可以近似的将加速度计的标度系数看成是相等的, 则计算式为:

$\begin{matrix} \frac{α_{K_{11}} + α_{K_{21}} + α_{K_{31}} + α_{K_{41}}}{4} = 15.225 ppm / ℃ (16) \end{matrix}$

从上式(16)可以看出, 温度系数在式(11)的范围内, 不能完全满足设计要求。按照式(14)的分析, 标度系数的温度系数有正有负, 将加速度计进行两两组合, 一正一负, 互相抵消, 使得a₁+a₂+a₃+a₄=0。选取编号5的加速度计代替编号1加速度计, 代入式(16)为:

$\begin{matrix} \frac{α_{K_{51}} + α_{K_{21}} + α_{K_{31}} + α_{K_{41}}}{4} = 1.075 ppm / ℃ (17) \end{matrix}$

从式(17)的结果可以看到, 温度系数之和降低了一个数量级, 并且满足式(12)对温度系数的要求, 这样就可以忽略温度系数直接对重力梯度测量的影响。通过对加速度计的温度系数进行选择, 在满足其他要求的情况下, 选择温度系数为两正两负, 并且温度系数的绝对值较接近, 根据式(14) 进行配对使用, 使得温度系数之和小于2 ppm。

4 结论

在不考虑环境振动等因素条件下, 取重力梯度仪两个通道量程为5 000 Eu和400 Eu, 温度变化范围为0.1℃~10℃, 最小误差为0.1~10 Eu的条件下, 代入推导的加速度计温度系数与重力梯度测量系统的关系式, 可得加速度计标度系数的温度系数变化范围为2× 10^-6~0.02; 针对加速度计温度系数一致性问题, 通过选取正负温度系数加速度计配对使用, 使得满足系统对温度系数性能指标的要求。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	曾华霖. 重力梯度测量的现状及复兴[J]. 物探与化探, 1999, 23(1): 1-6. [本文引用:1]
[2]	张金焕, 李晓斌. 航空重力梯度测量系统发展及现状[J]. 中国矿业, 2011, 20(增刊): 188-192. [本文引用:1]
[3]	张昌达. 几种新型的航空重力测量系统和航空重力梯度测量系统[J]. 物探与化探, 2005, 29(6): 474-476. [本文引用:1]
[4]	Murphy C A. Recent Developments with Air-FTG[C]//ASEG-PESA Airborne Gravity 2010 Workshop. [S. I. ]: Geoscience Australia, 2010: 142-151. [本文引用:1]
[5]	Difrancesco D, Grierson A, Kaputa D, et al. Gravity gradiometer systems-advances and challenges[J]. Geophysical Prospecting, 2009, 57(4): 615-623. [本文引用:1]
[6]	李海兵, 蔡体菁. 旋转加速度计重力梯度仪误差分析[J]. 中国惯性技术学报, 2009, 17(5): 525-528. [本文引用:1]
[7]	罗嗣成. 旋转加速度计重力梯度仪[D]. 武汉: 华中科技大学, 2007. [本文引用:2]
[8]	涂良成, 刘金全, 王志伟, 等. 旋转重力梯度仪的加速度计动态调节方法与需求分析[J]. 中国惯性技术学报, 2011, 19(2): 131-135. [本文引用:1]
[9]	王伟, 高维, 李成锁, 等. 重力梯度仪平台双向温控设计[J]. 物探与化探, 2015, 39(增刊): 17-21. [本文引用:1]
[10]	李纪莲, 张玘, 张开东. 航空重力测量比力温控系统热优化设计[J]. 中国惯性技术学报, 2013, 21(2): 155-158. [本文引用:1]
[11]	邓肖丹. 航空重力仪恒温系统研制[D]. 北京: 中国地质大学(北京), 2014. [本文引用:1]
[12]	孙洁洁, 李海兵, 丁祝顺, 等. 石英挠性加速度计的热分析[J]. 导航与控制, 2017, 16(1): 38-43. [本文引用:1]
[13]	郭纬川, 马杰, 楚贤, 等. 重力仪散热装置的热仿真分析[J]. 导航定位与授时, 2015, 2(2): 63-66. [本文引用:1]
[14]	陈仲恒, 屈孝池, 王佳民. 惯性平台台体热分析[J]. 导航与控制, 2005, 4(1): 3-7. [本文引用:1]
[15]	刘攀龙. 石英挠性加速度计的标定与温度补偿研究[D]. 长沙: 国防科学技术大学, 2008. [本文引用:1]
[16]	唐永超. 石英挠性加速度计力矩器热磁耦合仿真与试验研究[D]. 长沙: 国防科学技术大学, 2012. [本文引用:1]
[17]	陈仲恒, 屈孝池, 王佳民. 惯性平台系统热设计综述与展望[J]. 导航与控制, 2004, 3(3): 75-79. [本文引用:1]
[18]	陆元九, 等. 惯性器件[M]. 北京: 宇航出版社, 1993. [本文引用:2]
[19]	朱中平, 薛剑锋, 等. 中外磁性材料实用手册[M]. 北京: 中国物资出版社, 2004. [本文引用:1]

1999

0.0

2011

0.0

2005

0.0

2010

0.0

... 目前,国外实际投入使用的重力梯度测量系统是旋转加速度计重力梯度仪^[4,5],我国重力梯度仪研制起步较晚,面临的问题还较多,旋转加速度计重力梯度仪还处于原理样机阶段 ...

2009

0.0

2009

0.0

... 利用牛顿第二运动定律可得圆盘上的加速度计检测质量中心感受到的加速度为^[6,7,8]: ...

2007

0.0

... 利用牛顿第二运动定律可得圆盘上的加速度计检测质量中心感受到的加速度为^[6,7,8]: ...

... 为工作气隙磁感应温度系数,从磁性材料手册查到部分永磁合金属性如下表1所示,由表格中的数值可以看到磁感应温度系数较大,最小的温度系数也比导线的线胀系数高一个数量级,且都为负的温度系数,一般通过磁补偿的方式对温度系数进行补偿^[7] ...

2011

0.0

... 利用牛顿第二运动定律可得圆盘上的加速度计检测质量中心感受到的加速度为^[6,7,8]: ...

2015

0.0

2013

0.0

2017

0.0

2015

0.0

2005

0.0

2008

0.0

... 工程应用中,加速度计的输入输出数学模型一般只考虑零位偏置、标度系数,其公式为^[15], ...

2012

0.0

2004

0.0

1993

0.0

... 其中:V为加速度计输出电压,K₀为加速度计零偏,石英挠性加速度计的标度系数K₁可近似地用下式表示^[18]: ...

... 的导数为^[18]: ...

2004

0.0