基于实测积累电荷静电场消除静态效应的方法

引用本文

李国瑞, 席振铢, 龙霞. 基于实测积累电荷静电场消除静态效应的方法[J]. 物探与化探, 2017,41(4): 730-735.
LI Guo-Rui, XI Zhen-Zhu, LONG Xia. Static displacement correction for frequency domain electromagnetic method based on second electrostatic field[J]. Geophysical and Geochemical Exploration, 2017,41(4): 730-735.
Doi:10.11720/wtyht.2017.4.23 复制到剪切板

Permissions

《物探与化探》编辑部

基于实测积累电荷静电场消除静态效应的方法

李国瑞¹, 席振铢^2,³, 龙霞⁴

1.中水北方勘测设计研究有限责任公司,天津 300222

2.中南大学地球科学与信息物理学院,湖南长沙 410083

3.中南大学有色金属成矿预测与地质环境监测教育部重点实验室,湖南长沙 410083

4.湖南五维地质科技有限公司,湖南长沙 410205

席振铢(1966-),男,教授,博士生导师,主要从事电磁法理论与应用研究工作。Email:xizhenzhu@163.com

作者简介: 李国瑞(1990-),男,毕业于中南大学,工学硕士,主要从事电磁法探测技术的研究工作。Email:923846542@qq.com

收稿日期: 2016-12-11

基金: 国家自然科学基金(41304090)国家重点研发计划课题(2016YFC0303104)

摘要

频域电磁测深法存在的静态效应问题是由地表浅层电性不均匀体在一次天然电场作用下不均匀体界面积累电荷引起的。积累电荷引起的二次静电场与一次天然电场成线性关系,且二次电场与一次电场的比值 K只和地下介质的电性有关,地下介质的电性不变,则 K值不变。因此,利用人工源供电的方法,在供电时测量测点一次场和二次场的总场 E_t;断电后测量二次场 E₂,然后求取 K值,利用各测点的 K值和大地电磁法实测电场计算一次电场,进行静态校正。本文采用有限元二维大地电磁正演模拟地下浅层电性不均匀体产生的静态效应,利用 K值校正静态效应,获得了成功。结果显示这种方法能有效压制静态效应,达到静态校正的目的。

关键词: 大地电磁测深; 静态效应; 静态校正; 积累电荷; 人工供电; 二次电场

中图分类号:P631 文献标志码:A 文章编号:1000-8918(2017)04-0730-06

Static displacement correction for frequency domain electromagnetic method based on second electrostatic field

LI Guo-Rui¹, XI Zhen-Zhu^2,³, LONG Xia⁴

1.China Water Resources Beifang Investigation,Design & Research CO. LTD.,Tianjin 300222,China;

2.School of Geosciences and Info-Physics,Central South University,Changsha 410083,China

3.Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University),Ministry of Education,Changsha 410083,China

4.Hunan 5D Geological Science and Technology Co., Ltd.,Changsha 410205,China

Abstract

The static effect of the magnetotelluric sounding method is caused by stored charge on shallow layer electrical inhomogeneity by primary electric field. The induced second electric field caused by the accumulated charge is proportional to the primary electric field, and ratio coefficient K is only related to the electrical property of the underground media. The dielectric properties of the underground media are unchanged, and the K value is unchanged. Therefore, the method of artificial source is used to measure the total field of E_t in power supply; the induced electric field E₂ is measured in the off instantly, and then the proportion coefficient of K between the two data is calculated. K and measured electric field of the magnetotelluric sounding method are used to correct static effect, the finite element 2D MT forward modeling are employed to calculate the static effect produced by the underground electric uneven body, and K is used to correct static effect, thus achieving success. The results show that this method can effectively suppress the static effect and achieve the goal of static correction.

Keyword: MT; static effect; static correction; stored charge; artificial source; induced electric field

Show Figures

0 引言

1950年杰洪诺夫(Tichonov)、1953年卡尼亚(Cagnaird)先后提出了基于平面电磁波理论计算卡尼亚电阻率的频率域电磁测深法— 大地电磁测深(MT $\begin{matrix} )^{[12]} \end{matrix}$ , 随后在此基础上, 逐步发展出音频大地电磁测深法(AMT)和可控源音频大地电磁测深法(CSAMT), 它们在地质勘探领域中应用广泛^[3]。然而, 当近地表存在局部导电不均匀体时, 在外电场的作用下, 电流流过不均匀体界面, 不均匀体表面会产生积累电荷, 由此产生一个与外电场成正比的附加电场, 导致实测电场产生畸变, 根据实测电磁场计算的卡尼亚电阻率也随之产生畸变, 该畸变即为静态效应或静位移 $\begin{matrix} ^{[45]} \end{matrix}$ 。

因为近地表总是存在导电不均匀体, 所以基于计算卡尼亚电阻率的频率域电磁测深法的静态效应不可避免。静态效应影响异常的识别和资料的解释, 必须对其进行校正。目前, 国内外的校正静态效应的方法归结为3类:一是对各种地质模型的静态效应进行正演计算, 总结其影响规律 $\begin{matrix} ^{[58]} \end{matrix}$ , 参考实测资料, 采用人工平移的方法校正静态效应 $\begin{matrix} ^{[910]} \end{matrix}$ ; 二是采用空间滤波、相位积分、小波分析以及张量分解的方法压制静态效应 $\begin{matrix} ^{[1116]} \end{matrix}$ ; 三是采用没有静态效应的瞬变电磁法 $\begin{matrix} ^{[1718]} \end{matrix}$ 、音频磁场测深法^[19]校正静态效应。虽然上述方法都取得了一定效果, 但是, 上述3类方法均容易出现静位移识别不准, 校正不足或校正过量的问题。因此, 寻找一种能准确校正静态效应, 具有更大适用性的静位移校正方法意义重大。

1 基本理论

大地介质在平面电磁波一次电场作用下产生传导电流, 满足电荷守恒定律。根据欧姆定律、电荷守恒定律以及高斯定理, 可以推导出电阻率ρ 在频率域中的表达式

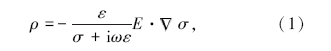
式中:ε 为介电常数, σ 为电导率, E为电场强度, ω 为角频率。在大地介质中, σ ≫iω ε , 因此可以将式(1)简化为

为一次电场方向的电导率梯度, 所以

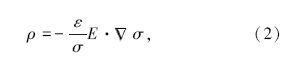
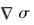
只有当大地介质的电导率不均匀时, 才有可能存在积累电荷的分布。在电导率均匀的导电媒质中, 电导率梯度为0, 因此积累电荷体密度为0, 表明均匀导电媒质中的积累电荷只能分布在导电媒质的表面上。因此总电荷密度可由表面电荷密度代替。根据库仑定律得出其二次电场

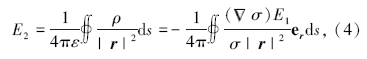
其中, ds为分布有电荷的表面上的面积微元, r表示面元ds与观测点间的向量, e_r表示沿r方向的单位向量。

简化式(4)等号右侧除E₁外的部分为一常数K, 则K与一次电场E₁无关, 只与导电不均匀体尺寸、导电不均匀体到观测点间的距离以及导电不均匀体与大地介质之间的电导率有关, 所以:

$\begin{matrix} E_{2} = K E_{1} 。 (5) \end{matrix}$

由式(5)得出二次电场与一次电场成正比例关系, 并且两者相位相同^[20]。

假设平面电磁波垂直入射一理想介质, 该介质上有AB两点, A点不受静态影响, B点受静态影响, 地表观测到的电场分别为E_A和E_B:

$\begin{matrix} E_{B} = (1 + K) E_{A}, (6) \end{matrix}$

将式(6)代入卡尼亚视电阻率公式得

$\begin{matrix} \begin{matrix} {ρ_{B}}_{Ω \cdot m} = {|\frac{{E_{B}}_{mV / km}}{{E_{A}}_{mV / km}}|}^{2} {ρ_{A}}_{Ω \cdot m}, (7) \\ {ρ_{B}}_{Ω \cdot m} = | 1 + K |^{2} {ρ_{A}}_{Ω \cdot m}, (8) \end{matrix} \end{matrix}$

上式两边取对数则有

$\begin{matrix} lo g_{10} {ρ_{B}}_{Ω \cdot m} = lo g_{10} | 1 + K |^{2} + lo g_{10} {ρ_{A}}_{Ω \cdot m}, (9) \end{matrix}$

log₁₀|1+K|²是常数, 因此在双对数坐标系中, 不受静态影响的A点测深曲线与受测深影响的B点测深曲线会在视电阻率轴上发生平移而整体趋势不变, 相位曲线不变。

2 静态校正

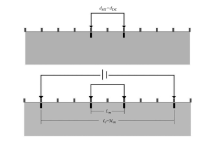
由于K与一次电场无关, 因此, 可以运用人工源供电测量的方法得到K值。供电电极和测量电极的排列如图1所示, 同一测点上, 人工源供电时测量电极距离d_DC和频率域电磁测深法测量电极距离d_MT相同。在直流电源供电时, 供电正负电极和测量正负电极在同一直线上并关于测点对称, 且供电电极距视具体情况而定, 以使其产生的电流覆盖浅层电性不均匀体为宜, 文中设定供电电极距≥ 3倍的测量电极极距。

	Figure Option View Download New Window
	图1 利用人工源供电测量K值装置

在频率域电磁测深法采集数据前, 利用人工直流电源向供电电极供入直流电, 同时观测测量电极上的电压, 当测量电极电压稳定后, 记录该电压值U, 并停止供电。由于人工源产生的一次电场消失, 只剩余积累电荷产生的二次电场, 所以测量电极上电压值发生跃变, 之后随时间按指数规律衰减, 跃变后测量电极电压为U₂。

得到U和U₂, 按公式 $\begin{matrix} K = U_{2} / (U - U_{2}) \end{matrix}$ 计算K值, 就可以校正地下电性不均匀体产生的静态校应:

$\begin{matrix} E_{c} = \frac{1}{(1 + K)} E_{m}, (10) \end{matrix}$

其中, E_c是校正静态效应后的电场, E_m是频域电磁测深观测得到的电场。

3 数值模拟

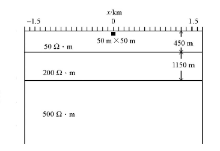
为验证该方法的可行性, 设计了数值模拟实验, 通过有限元二维正演数值模拟来分析不同情况下静态效应现象及其校正效果。有限元二维正演网格剖分为35× 31, 数值模拟测深点 36个, 测深频点 26个, 频率范围0.01~1 000 Hz(以下模型测深点与频点相同)。地电模型为均匀层状大地背景下浅层存在异常体。图2为设计的均匀三层地电模型, 上地层电阻率为50 Ω · m, 厚度450 m; 第二层电阻率为200 Ω · m, 厚度1 150 m; 下层电阻率为500 Ω · m, 厚度延伸较大。在0 km位置处的正下方设置一电性不均匀体, 其电阻率ρ ₀分别设置为50、10、5、250、500 Ω · m。

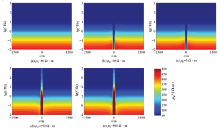
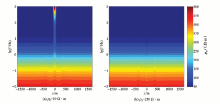
	Figure Option View Download New Window
	图2 均匀大地背景存在浅层不均匀体的地电模型

利用有限元二维大地电磁正演方法对上述地电模型计算, 得到图3所示的视电阻率拟断面。图中给出了TM 极化模式下均匀层状大地背景中的静态效应模拟结果, 从等值线的变化可以看出, 近地表存在电性不均匀体时, 视电阻率值受静态效应的影响严重。当近地表不均匀体为低阻时, 其所在位置下方各频点视电阻率较正常值偏低, 拟断面表现为下凹; 当近地表不均匀体为高阻时, 其所在位置下方各频点视电阻率较正常值偏高, 拟断面表现为上凸。

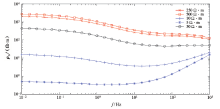
	Figure Option View Download New Window
	图3 不均匀体存在于均匀层状介质时视电阻率拟断面

为了观察不均匀体对同一测点各频点的干扰, 选择其上方的0号点为研究对象。图4给出了不均匀体电阻率不同时的频率— 视电阻率曲线对比。可以看出:当异常体存在时, 0点视电阻率曲线整体上移或下移; 当异常体为高阻时, 曲线整体向上移动而趋势不变; 当异常体为低阻时, 曲线整体向下移动。在高频时曲线趋势发生变化, 这是由于低阻不均匀体在一次电场下内部发生电磁感应引起的, 并且电阻越低, 电磁感应越强。

	Figure Option View Download New Window
	图4 0号点视电阻率曲线

分别选取不均匀体电阻率为250、10 Ω · m时的均匀层状介质模型为例进行静态校正, 表1为数值模拟结果。 $\begin{matrix} E_{2.5119}^{50} \end{matrix}$ 、 $\begin{matrix} E_{2.5119}^{10} \end{matrix}$ 、 $\begin{matrix} E_{2.5119}^{250} \end{matrix}$ 为异常体电阻率分别为50、10、250 Ω · m、频率为2.5119 Hz的电场值。当异常体电阻率为50 Ω · m时, 计算得到的电场 $\begin{matrix} E_{2.5119}^{50} \end{matrix}$ 等价于没有异常体时的一次电场, $\begin{matrix} E_{2.5119}^{10} \end{matrix}$ 、 $\begin{matrix} E_{2.5119}^{250} \end{matrix}$ 等价于异常体电阻率为250 Ω · m和10 Ω · m时的总场。计算得到 $\begin{matrix} K_{2.5119}^{10} \end{matrix}$ 、 $\begin{matrix} K_{2.5119}^{250} \end{matrix}$ , 1/(1+K)是根据式(5)计算得到的静态校正系数。

表1 导电不均匀体电阻率为250 Ω · m和10 Ω · m时的数值模拟结果

测点	$\begin{matrix} E_{2.5119}^{50} \end{matrix}$		$\begin{matrix} E_{2.5119}^{10} \end{matrix}$		$\begin{matrix} E_{2.5119}^{250} \end{matrix}$		$\begin{matrix} K_{2.5119}^{10} \end{matrix}$		$\begin{matrix} K_{2.5119}^{250} \end{matrix}$		$\begin{matrix} \frac{1}{(1 + K_{2.5119}^{10})} \end{matrix}$	$\begin{matrix} \frac{1}{(1 + K_{2.5119}^{250})} \end{matrix}$
1	-0.00093		-0.00093		-0.00093		0.000753		-0.00107		1.00	1.00
2	-0.00093		-0.00093		-0.00093		0.000757		-0.00108		1.00	1.00
3	-0.00093		-0.00093		-0.00093		0.000769		-0.00109		1.00	1.00
4	-0.00093		-0.00093		-0.00093		0.000789		-0.00112		1.00	1.00
5	-0.00093		-0.00093		-0.00093		0.00082		-0.00117		1.00	1.00
6	-0.00093		-0.00093		-0.00093		0.000862		-0.00123		1.00	1.00
7	-0.00093		-0.00093		-0.00093		0.000921		-0.00131		1.00	1.00
8	-0.00093		-0.00093		-0.00093		0.001003		-0.00143		1.00	1.00
9	-0.00093		-0.00093		-0.00093		0.001122		-0.0016		1.00	1.00
10	-0.00093		-0.00093		-0.00093		0.0013		-0.00185		1.00	1.00
11	-0.00093		-0.00093		-0.00093		0.001584		-0.00225		1.00	1.00
12	-0.00093		-0.00093		-0.00093		0.002056		-0.00292		1.00	1.00
13	-0.00093		-0.00093		-0.00093		0.002943		-0.00418		1.00	1.00
14	-0.00093		-0.00094		-0.00093		0.004487		-0.00638		1.00	1.01
15	-0.00093		-0.00094		-0.00092		0.008447		-0.01201		0.99	1.01
16	-0.00093		-0.00095		-0.00091		0.016233		-0.02308		0.98	1.02
17	-0.00093		-0.00096		-0.00089		0.028864		-0.04103		0.97	1.04
18	-0.00093		-0.00017		-0.00201		-0.81467		1.157995		5.40	0.46
19	-0.00093		-0.00017		-0.00201		-0.81467		1.157995		5.40	0.46
20	-0.00093		-0.00096		-0.00089		0.028864		-0.04103		0.97	1.04
21	-0.00093		-0.00095		-0.00091		0.016233		-0.02308		0.98	1.02
22	-0.00093		-0.00094		-0.00092		0.008447		-0.01201		0.99	1.01
23	-0.00093		-0.00094		-0.00093		0.004487		-0.00638		1.00	1.01
24	-0.00093		-0.00093		-0.00093		0.002943		-0.00418		1.00	1.00
25		-0.00093		-0.00093		-0.00093		0.002056		-0.00292	1.00	1.00
26		-0.00093		-0.00093		-0.00093		0.001584		-0.00225	1.00	1.00
27		-0.00093		-0.00093		-0.00093		0.0013		-0.00185	1.00	1.00
28		-0.00093		-0.00093		-0.00093		0.001122		-0.0016	1.00	1.00
29		-0.00093		-0.00093		-0.00093		0.001003		-0.00143	1.00	1.00
30		-0.00093		-0.00093		-0.00093		0.000921		-0.00131	1.00	1.00
31		-0.00093		-0.00093		-0.00093		0.000862		-0.00123	1.00	1.00
32		-0.00093		-0.00093		-0.00093		0.00082		-0.00117	1.00	1.00
33		-0.00093		-0.00093		-0.00093		0.000789		-0.00112	1.00	1.00
34		-0.00093		-0.00093		-0.00093		0.000769		-0.00109	1.00	1.00
35		-0.00093		-0.00093		-0.00093		0.000757		-0.00108	1.00	1.00
36		-0.00093		-0.00093		-0.00093		0.000753		-0.00107	1.00	1.00

表1 导电不均匀体电阻率为250 Ω · m和10 Ω · m时的数值模拟结果

根据式(5), 利用表1中静态校正系数来校正静态效应, 图5为校正后的视电阻率拟断面。从图5b中看出, 高阻不均匀体引起的静态畸变几乎得到了完全消除。在图5a中, 低阻不均匀体引起的静态畸变在低频段得到了完全消除, 在高频段由于电磁感应的原因校正过头产生了高阻。综合来看, 该方法达到了校正静态效应的目的。

	Figure Option View Download New Window
	图5 利用K值校正后的视电阻率拟断面

4 结论

1)地表浅层不均匀体在一次电场作用下边界面积累电荷产生二次电场叠加在一次电场之上, 造成了频域电磁测深法中的静态效应, 使单点电阻率曲线整体发生平移, 而不改变其趋势。

2)高阻不均匀体使受影响测点的视电阻率整体向上移动而趋势不变, 并且不均匀体电阻率越高, 视电阻率向上平移的幅度越大; 低阻不均匀体使受影响测点的视电阻率整体向下移动, 并且由于电磁感应现象, 单点视电阻率曲线在高频段趋势发生变化。不均匀体电阻越低, 视电阻率向下平移的幅度越大, 高频段曲线趋势畸变越严重。

3)积累电荷引起的二次电场与一次电场成正比关系。求取二者间的比例系数来校正静态效应在理论上可行, 并能取得理想的校正效果。但是由于低阻不均匀体的电磁感应现象, 使用该方法对低阻不均匀体引起的静态效应进行校正, 会在高频段出现校正过头的现象。

4)由于积累电荷按指数规律衰减, 要测量断电时瞬间的二次电场, 需要仪器硬件方面的配合才能实现。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	陈乐寿. 大地电磁测深方法[M]. 北京: 地质出版社, 1990. [本文引用:1]
[2]	李金铭. 地电场与电法勘探[M]. 北京: 地质出版社, 2005. [本文引用:1]
[3]	杨长福, 徐世浙. 国外大地电磁研究现状[J]. 物探与化探, 2005, 29(3): 243-246. [本文引用:1]
[4]	严家斌. 大地电磁信号处理理论及方法研究[D]. 长沙: 中南大学, 2003. [本文引用:1]
[5]	伍亮, 李桐林, 朱成, 等. 大地电磁测深法中静态效应及其反演[J]. 地球物理学进展, 2015, 30, (2): 840-846. [本文引用:1]
[6]	陈辉. 可控源音频大地电磁法静态效应校正技术及其方法研究[D]. 武汉: 中国地质大学, 2007. [本文引用:1]
[7]	万汉平. 大地电磁测深的TE和TM极化模式对比研究 [D]. 成都: 成都理工大学, 2010. [本文引用:1]
[8]	阎述, 陈明生. 频率域电磁测深的静态偏移及校正方法[J]. 石油地球物理勘探, 1996, 31(2): 238-247. [本文引用:1]
[9]	苏鸿尧, 何展翔. 表层电性不均匀对大地电磁测深曲线的畸变研究[J]. 地质科技情报, 2000, 19(3): 103-106. [本文引用:1]
[10]	段波. 校正大地电磁测深中静态效应的首支重合法[J]. 长春地质学院学报, 1994, 24(4): 444-447. [本文引用:1]
[11]	梁生贤, 张胜业, 祁晓雨, 等. 基于空间滤波和相位换算的MT静校正方法比较[J]. 工程地球物理学报, 2010, 7(3): 302-306. [本文引用:1]
[12]	罗志琼. 用电磁阵列法压制MT静态效应的研究[J]. 地球科学, 1990, 15(S): 13-22. [本文引用:1]
[13]	张翔, 胡文宝, 严良俊. 小波变换在大地电磁测深静校正中的应用[J]. 江汉石油学院学报, 2002, 24(2): 40-43. [本文引用:1]
[14]	杨生, 鲍光淑, 李爱勇. MT法中静态效应及阻抗张量静态校正法[J]. 中南工业大学学报, 2002, 33(1): 8-13. [本文引用:1]
[15]	宋守根, 汤井田, 何继善. 小波分析与电磁测深中静态效应的识别、分离及压制[J]. 地球物理学报, 1995, 38(1): 120-128. [本文引用:1]
[16]	张全胜, 王家映. 大地电磁测深资料的去噪方法[J]. 石油地球物理勘探, 2004, 39(S): 17-23. [本文引用:1]
[17]	鲁新便, 田春来, 李貅. 瞬变电磁测深法在大地电磁测深曲线静校正中的应用[J]. 石油物探, 1995, 34(1): 86-95. [本文引用:1]
[18]	姚治龙, 王庆乙, 胡玉平, 等. 利用TEM测深校正MT静态偏移的技术问题[J]. 地震地质, 2001, 23(2): 257-263. [本文引用:1]
[19]	冯万杰. 可控源音频磁场测深法2. 5D正演计算[D]. 长沙: 中南大学, 2012. [本文引用:1]
[20]	Louis Cagniard. Basic Theory of the Magneto-telluric Method of Geophysical prospecting[J]. Geophysics, 1953, 18(3): 605-635. [本文引用:1]