基于Zoeppritz方程的纵横波模量反演

引用本文

冉然, 宋建国. 基于Zoeppritz方程的纵横波模量反演[J]. 物探与化探, 2017,41(4): 707-714.
RAN Ran, SONG Jian-Guo. Compressional and shear modulus inversion based on Zoeppritz equation[J]. Geophysical and Geochemical Exploration, 2017,41(4): 707-714.
Doi:10.11720/wtyht.2017.4.19 复制到剪切板

Permissions

《物探与化探》编辑部

基于Zoeppritz方程的纵横波模量反演

冉然, 宋建国

中国石油大学(华东) 地球科学与技术学院,山东青岛 266555

作者简介: 冉然(1990-),男,硕士研究生,主要研究方向为地球物理数据处理及方法研究。

收稿日期: 2016-09-19

摘要

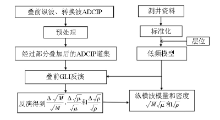
叠前地震反演的主要目的是根据地震数据精确地求取地下介质的弹性参数,进而进行流体识别和油藏描述。常规叠前反演方法使用Zoeppritz方程近似式计算反射系数,但是含有丰富信息的大偏移距地震数据无法被有效利用,针对这个问题,将纵横波模量引入Zoeppritz方程,建立了基于Zoeppritz方程的纵横波模量广义线性反演方法,适用于大角度地震数据。模型测试和实际地震资料应用表明,此方法能够可靠的得到地下介质的纵横波模量,相对于间接反演减小了间接反演带来的累积误差,为后续流体识别和含油气检测提供了很好的数据基础。

关键词: 叠前地震反演; 直接反演; 纵横波模量; Zoeppritz方程

中图分类号:P631.4 文献标志码:A 文章编号:1000-8918(2017)04-0707-08

Compressional and shear modulus inversion based on Zoeppritz equation

RAN Ran, SONG Jian-Guo

School of geosciences,China University of Petroleum (East China),Qingdao 266555,China

Abstract

The main purpose of pre-stack seismic inversion lies in getting elastic parameters of underground media and then making liquid identification and reservoir description.In this paper the authors tried to eliminate the inherent trouble that long offset seismic data could not be used efficiently when the approximate Zoeppritz equation is adopted.The authors start with the Zoeppritz equation of P-wave and S-wave velocity and obtain the Zoeppritz equation of compressional and shear modulus.Then,with the new Zoeppritz equation,the authors start the direct compressional and shear modulus inversion based on the generalized linear inversion theory and apply the means to seismic data with all angles.Model and practical test shows that the method is stable and reasonable in obtaining the compressional and shear modulus,and can reduce the cumulative error which is caused by the common elastic inversion method.The result obtained by the authors provides good data basis for the liquid detection and identification.

Keyword: pre-stack seismic inversion; direct inversion; compressional and shear modulus; Zoeppritz equation

Show Figures

0 引言

地震勘探对油气田的开采开发有着至关重要的指导作用, 如何从地震数据中更精确地得到地下介质的弹性参数一直是进行地震反演工作的关键问题。不同于叠后反演只能得到波阻抗, 叠前地震反演能够精确地从地震数据中获得各项弹性参数。国内外许多学者针对叠前反演做了大量的理论研究和实践分析。Cooke^[1]最早建立了广义线性反演理论(GLI), 并且应用于地震反演中。Macdonald^[2]等对将广义线性反演方法针对Zoeppritz方程的线性程度进行了研究。Fatti^[3]使用加权叠加法计算纵横波阻抗, 第一次在反演中引入密度项而非使用Gardner公式进行拟合。Simmons^[4]应用线性反演方法获得纵横波阻抗和密度, 不足之处在于使用了Gardner公式。Goodway等^[5]建立了基于拉梅常数的反演技术(LMR), 实现了弹性参数的直接反演。Buland等^[6]研究了基于贝叶斯理论的线性反演方法。杨培杰等 $\begin{matrix} ^{[79]} \end{matrix}$ 研究支持向量机的叠前地震反演方法和非线性二次约束叠前反演方法, 并最终建立基于贝叶斯理论的流体因子直接反演方法。宗兆云等 $\begin{matrix} ^{[1012]} \end{matrix}$ 建立了基于弹性阻抗反演方法直接获得拉梅常数, 纵横波模量以及杨氏模量和泊松比的叠前地震反演方法。张广智^[13]针对页岩气建立了基于弹性阻抗反演方法直接求取杨氏模量和密度的乘积以及泊松比的方法。但是这些方法由于均使用了Aki& Richard近似式求取反射系数, 无法应用于大角度地震数据中。张丰麒^[14]基于广义线性反演理论建立了纵横波联合反演纵波速度、横波速度和密度的方法, 该方法直接使用Zoeppritz方程进行反射系数的求取, 有效避免了由于使用近似式导致的大角度地震数据无法被有效利用的缺陷。周林等^[15]利用精确Zoeppritz方程进行了AVO三参反演, 并验证了大角度地震数据能够有效提高反演精度, 尤其是对于密度反演结果。

叠前地震反演的根本目的是流体识别和储层预测, 如何有效地利用反演得到的弹性参数来分辨出地下介质中的流体一直以来都是人们研究的重点目标^[16], Goodway^[5]等人建立的LMR算法将拉梅常数作为流体异常识别因子, 相对于纵横波速度具有较高的准确性。Russell等^[17]建立了Russell流体因子, 该流体因子基于Biot-Gassmann理论, 并假设孔隙中为饱和流体, 忽略了孔隙中流体在非饱和的情况, 宗兆云^[11]对Russell流体因子进行了改进, 将流体因子由纵横波阻抗和密度的函数改进为纵横波模量的函数, 郝前勇^[18]研究了多弹性参数和流体因子之间的定量关系, 并结合地震、测井和地质信息实现综合的流体识别和储层预测。

笔者所建立的叠前纵横波模量地震反演是基于广义线性反演理论, 并且直接使用了Zoeppritz方程进行反射系数的求取。相对于其他方法, 本方法能够有效地利用大角度的叠前地震数据, 并且避免了由于间接反演纵横波模量所导致的累积误差, 能够更精确的根据叠前地震数据得到地下介质的纵横波模量, 并且可以有效的进行流体识别。

1 基于精确Zoeppritz方程的纵横波模量地震反演

Zoeppritz方程是AVO分析技术的理论基础。根据弹性波动力学的理论, P波入射到反射界面上时, 会产生反射P波、反射SV波、透射P波、透射SV波。1919年, 德国数学家Zoeppritz基于弹性波动理论, 推导得到了反射系数和透射系数的表达公式。该方程是反射、透射系数与入射角度、速度、密度的函数, 称为Zoeppritz方程:

$\begin{matrix} [\begin{matrix} sinα & cosβ & - sinα' & cosβ' \\ cosα & - sinβ & cosα' & sinβ' \\ \sin 2 α & \frac{v_{p 1}}{v_{s 1}} \cos 2 β & \frac{v_{p 1}}{v_{p 2}} \frac{v_{s 2}^{2}}{v_{s 1}^{2}} \frac{ρ_{2}}{ρ_{1}} \sin 2 α' & - \frac{v_{p 1} v_{s 2}}{v_{s 1}^{2}} \frac{ρ_{2}}{ρ_{1}} \cos 2 β' \\ \cos 2 β & - \frac{v_{s 1}}{v_{p 1}} \sin 2 β & - \frac{ρ_{2}}{ρ_{1}} \frac{v_{p 2}}{v_{p 1}} \cos 2 β' & - \frac{ρ_{2}}{ρ_{1}} \frac{v_{s 2}}{v_{p 1}} \sin 2 β' \end{matrix}] [\begin{matrix} R_{pp} \\ R_{ps} \\ T_{pp} \\ T_{ps} \end{matrix}] = [\begin{matrix} - sinα \\ cosα \\ - \sin 2 α \\ - \cos 2 β \end{matrix}] (1) \end{matrix}$

式(1)中:v_p, v_s分别为纵横波速度; ρ 为密度; R_pp, R_ps分别为反射P波和反射SV波的反射系数; T_pp, T_ps分别为透射P波和透射SV波的透射系数; α , β , α ', β '分别为P波入射角度, SV波反射角度, P波透射角度, SV波透射角度。

在理想介质中, 纵横波速度和纵横波模量之间的关系为^[11]:

$\begin{matrix} \begin{matrix} v_{p} = \sqrt{M / ρ}, (2) \\ v_{s} = \sqrt{μ / ρ} 。 (3) \end{matrix} \end{matrix}$

其中:M为纵波模量, μ 为横波模量。将式(2)、(3)代入方程(1)中就可以得到纵横波模量的Zoeppritz方程:

$\begin{matrix} [\begin{matrix} sinα & cosβ & - sinα' & cosβ' \\ cosα & - sinβ & cosα' & sinβ' \\ \sin 2 α & \sqrt{\frac{M_{1}}{μ_{1}}} \cos 2 β & \sqrt{\frac{M_{1}}{M_{2}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \frac{μ_{2}}{μ_{1}} \sin 2 α' & - \sqrt{\frac{M_{1}}{μ_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \cos 2 β' \\ \cos 2 β & - \sqrt{\frac{μ_{1}}{M_{1}}} \sin 2 β & - \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{M_{2}}{M_{1}}} \cos 2 β' & - \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{μ_{2}}{M_{1}}} \sin 2 β' \end{matrix}] [\begin{matrix} R_{pp} \\ R_{ps} \\ T_{pp} \\ T_{ps} \end{matrix}] = [\begin{matrix} - sinα \\ cosα \\ - \sin 2 α \\ - \cos 2 β \end{matrix}] 。 (4) \end{matrix}$

设γ ₁= $\begin{matrix} \sqrt{M_{1} / μ_{1}} \end{matrix}$ , 方程(4)可变形为:

$\begin{matrix} [\begin{matrix} sinα & cosβ & - sinα' & cosβ' \\ cosα & - sinβ & cosα' & sinβ' \\ \sqrt{\frac{M_{2}}{M_{1}}} \sin 2 α & γ_{1} \cos 2 β & \sqrt{\frac{ρ_{2}}{ρ_{1}}} \frac{μ_{2}}{μ_{1}} \sin 2 α' & - γ_{1} \sqrt{\frac{M_{2}}{M_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \cos 2 β' \\ γ_{1} \cos 2 β & - \sin 2 β & - γ_{1} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{M_{2}}{M_{1}}} \cos 2 β' & - \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} \sin 2 β' \end{matrix}] [\begin{matrix} R_{pp} \\ R_{ps} \\ T_{pp} \\ T_{ps} \end{matrix}] = [\begin{matrix} - sinα \\ cosα \\ - \sqrt{\frac{M_{2}}{M_{1}}} \sin 2 α \\ - γ_{1} \cos 2 β \end{matrix}] 。 (5) \end{matrix}$

方程的推导是基于精确Zeoppritz方程, 在推导过程中并未对参数做任何的近似处理, 方程的精度是毋庸置疑的, 因此这里不需要对方程的适用角度进行研究和讨论。根据广义线性反演理论, Zeopptitz方程本身为非线性方程, 在构建反演方程时需要对其进行线性处理, 即对方程(5)各项分别求 $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ , $\begin{matrix} \sqrt{μ_{2} / μ_{1}} \end{matrix}$ , $\begin{matrix} \sqrt{ρ_{2} / ρ_{1}} \end{matrix}$ , γ ₁的一阶偏导, 为了方便表达可以将方程(5)简写成Z· R=C的形式, 其中Z为方程(5)左边系数项, R为方程(5)反射透射系数项, C为方程(5)右边常数项。

方程(5)对 $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ 的一阶偏导:

$\begin{matrix} Z [\begin{matrix} \frac{\partial R_{pp}}{\partial \sqrt{M_{2} / M_{1}}} \\ \frac{\partial R_{ps}}{\partial \sqrt{M_{2} / M_{1}}} \\ \frac{\partial T_{pp}}{\partial \sqrt{M_{2} / M_{1}}} \\ \frac{\partial T_{ps}}{\partial \sqrt{M_{2} / M_{1}}} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ \sin 2 α - R_{pp} \sin 2 α - R_{ps} γ_{1} \cos 2 β + T_{ps} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} γ_{1} \cos 2 β' \\ T_{pp} \sqrt{\frac{ρ_{2}}{ρ_{1}}} γ_{1} \cos 2 β' \end{matrix}] 。 (6) \end{matrix}$

方程(5)对 $\begin{matrix} \sqrt{μ_{2} / μ_{1}} \end{matrix}$ 的一阶偏导:

$\begin{matrix} Z [\begin{matrix} \frac{\partial R_{pp}}{\partial \sqrt{μ_{2} / μ_{1}}} \\ \frac{\partial R_{ps}}{\partial \sqrt{μ_{2} / μ_{1}}} \\ \frac{\partial T_{pp}}{\partial \sqrt{μ_{2} / μ_{1}}} \\ \frac{\partial T_{ps}}{\partial \sqrt{μ_{2} / μ_{1}}} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ - 2 T_{pp} \sqrt{\frac{μ_{2}}{μ_{1}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sin 2 α' + T_{ps} \sqrt{\frac{M_{2}}{M_{1}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} γ_{1} \cos 2 β' \\ \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sin 2 β' \end{matrix}] 。 (7) \end{matrix}$

方程(5)对γ ₁的一阶偏导:

$\begin{matrix} Z [\begin{matrix} \frac{\partial R_{pp}}{\partial γ_{1}} \\ \frac{\partial R_{ps}}{\partial γ_{1}} \\ \frac{\partial T_{pp}}{\partial γ_{1}} \\ \frac{\partial T_{ps}}{\partial γ_{1}} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ - R_{ps} \sqrt{\frac{M_{2}}{M_{1}}} \cos 2 β + T_{ps} \sqrt{\frac{M_{2}}{M_{1}}} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} \cos 2 β' \\ - \cos 2 β - R_{pp} \cos 2 β + T_{pp} \sqrt{\frac{ρ_{2}}{ρ_{1}}} \sqrt{\frac{M_{2}}{M_{1}}} \cos 2 β' \end{matrix}] 。 (8) \end{matrix}$

方程(5)对 $\begin{matrix} \sqrt{ρ_{2} / ρ_{1}} \end{matrix}$ 的一阶偏导:

$\begin{matrix} Z [\begin{matrix} \frac{\partial R_{pp}}{\partial \sqrt{ρ_{2} / ρ_{1}}} \\ \frac{\partial R_{ps}}{\partial \sqrt{ρ_{2} / ρ_{1}}} \\ \frac{\partial T_{pp}}{\partial \sqrt{ρ_{2} / ρ_{1}}} \\ \frac{\partial T_{ps}}{\partial \sqrt{ρ_{2} / ρ_{1}}} \end{matrix}] = [\begin{matrix} 0 \\ 0 \\ - T_{pp} \frac{μ_{2}}{μ_{1}} \sin 2 α' + T_{ps} \sqrt{\frac{M_{2}}{M_{1}}} \sqrt{\frac{μ_{2}}{μ_{1}}} γ_{1} \cos 2 β' \\ T_{pp} \sqrt{\frac{M_{2}}{M_{1}}} γ_{1} \cos 2 β' + \sqrt{\frac{μ_{2}}{μ_{1}}} \sin 2 β' \end{matrix}] 。 (9) \end{matrix}$

纵波和转换波的反射系数对着4个独立分量的一阶偏导方程由上面的公式给出, 通过给定的初始模型, 分别求解式(6)~(9)这4个独立的线性方程组, 即可得到反射系数对这4个独立分量的一阶偏导, 进而构建反演方程组:

$\begin{matrix} [\begin{matrix} _{1} R_{pp,_{\sqrt{M_{2} / M_{1}}}} & _{1} R_{pp,_{\sqrt{μ_{2} / μ_{1}}}} & _{1} R_{pp,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{1} R_{pp, γ_{1}} \\ _{2} R_{pp,_{\sqrt{M_{2} / M_{1}}}} & _{2} R_{pp,_{\sqrt{μ_{2} / μ_{1}}}} & _{2} R_{pp,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{2} R_{pp, γ_{1}} \\ ︙ & ︙ & ︙ & ︙ \\ _{n} R_{pp,_{\sqrt{M_{2} / M_{1}}}} & _{n} R_{pp,_{\sqrt{μ_{2} / μ_{1}}}} & _{n} R_{pp,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{n} R_{pp, γ_{1}} \\ _{1} R_{ps,_{\sqrt{M_{2} / M_{1}}}} & _{1} R_{ps,_{\sqrt{μ_{2} / μ_{1}}}} & _{1} R_{ps,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{1} R_{ps, γ_{1}} \\ _{2} R_{ps,_{\sqrt{M_{2} / M_{1}}}} & _{2} R_{ps,_{\sqrt{μ_{2} / μ_{1}}}} & _{2} R_{ps,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{2} R_{ps, γ_{1}} \\ ︙ & ︙ & ︙ & ︙ \\ _{n} R_{ps,_{\sqrt{M_{2} / M_{1}}}} & _{n} R_{ps,_{\sqrt{μ_{2} / μ_{1}}}} & _{n} R_{ps,_{\sqrt{ρ_{2} / ρ_{1}}}} & _{n} R_{ps, γ_{1}} \end{matrix}] [\begin{matrix} Δ \sqrt{\frac{M_{2}}{M_{1}}} \\ Δ \sqrt{\frac{μ_{2}}{μ_{1}}} \\ Δ \sqrt{\frac{ρ_{2}}{ρ_{1}}} \\ Δ γ_{1} \end{matrix}] = [\begin{matrix} _{1} \partial R_{pp} \\ _{2} \partial R_{pp} \\ ︙ \\ _{n} \partial R_{pp} \\ _{1} \partial R_{ps} \\ _{2} \partial R_{ps} \\ ︙ \\ _{n} \partial R_{ps} \end{matrix}] 。 (10) \end{matrix}$

方程(10)中左下标1~n分别代表角度域共成像点道集中的角度数; 方程左边系数矩阵中_n $\begin{matrix} R_{pp,_{\sqrt{M_{2} / M_{1}}}} \end{matrix}$ 表示反射系数R_pp对独立分量 $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ 的一阶偏导数, 其他各项亦是如此; ∂ R_pp和∂ R_ps分别代表地震数据反射系数和由初始模型通过Zoeppritz方程得到的反射系数的差。本方程即可计算纵横波联合反演, 亦可计算单PP波或者单PS波反演, 当叠前地震数据只有PP波数据时, 只需R_pp分量参与计算, R_ps分量需要舍弃; 当地震数据只有PS波数据时, 只需R_ps参与计算, R_pp分量需要舍弃; 当PP波数据和PS波数据同时具备时, R_pp分量和R_ps分量可同时参与计算。

通过求解方程(10), 可以得到4个独立分量的扰动量Δ $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ , Δ $\begin{matrix} \sqrt{μ_{2} / μ_{1}} \end{matrix}$ , Δ $\begin{matrix} \sqrt{ρ_{2} / ρ_{1}} \end{matrix}$ 和Δ γ ₁, 与初始模型相加即可得到新的反演后的模型 $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ 、 $\begin{matrix} \sqrt{μ_{2} / μ_{1}} \end{matrix}$ 、 $\begin{matrix} \sqrt{ρ_{2} / ρ_{1}} \end{matrix}$ 和γ ₁。根据AVO理论γ ₁分量对反射系数的影响较小, 因此在后续计算时需要将其舍弃, 同时将其他3个分量转化为各自的反射系数: $\begin{matrix} \frac{Δ \sqrt{M}}{\sqrt{M}} \end{matrix}$ , $\begin{matrix} \frac{Δ \sqrt{μ}}{\sqrt{μ}} \end{matrix}$ 以及 $\begin{matrix} \frac{Δ \sqrt{ρ}}{\sqrt{ρ}} \end{matrix}$ , 反演结果和反射系数之间的关系:

$\begin{matrix} \{\begin{matrix} \frac{Δ \sqrt{M}}{\sqrt{M}} = \frac{\sqrt{M_{2}} - \sqrt{M_{1}}}{(\sqrt{M_{2}} + \sqrt{M_{1}} \frac{)}{2}} = \frac{2 (\sqrt{M_{2}} / \sqrt{M_{1}} - 1)}{\sqrt{M_{2}} / \sqrt{M_{1}} + 1}, \\ \frac{Δ \sqrt{μ}}{\sqrt{μ}} = \frac{\sqrt{μ_{2}} - \sqrt{μ_{1}}}{(\sqrt{μ_{2}} + \sqrt{μ_{1}} \frac{)}{2}} = \frac{2 (\sqrt{μ_{2}} / \sqrt{μ_{1}} - 1)}{\sqrt{μ_{2}} / \sqrt{μ_{1}} + 1}, \\ \frac{Δ \sqrt{ρ}}{\sqrt{ρ}} = \frac{\sqrt{ρ_{2}} - \sqrt{ρ_{1}}}{(\sqrt{ρ_{2}} + \sqrt{ρ_{1}} \frac{)}{2}} = \frac{2 (\sqrt{ρ_{2}} / \sqrt{ρ_{1}} - 1)}{\sqrt{ρ_{2}} / \sqrt{ρ_{1}} + 1} 。 \end{matrix} (11) \end{matrix}$

反射系数结合低频数据进行低频补偿^[19]即可得到最终的反演结果 $\begin{matrix} \sqrt{M} \end{matrix}$ 、 $\begin{matrix} \sqrt{μ} \end{matrix}$ 和 $\begin{matrix} \sqrt{ρ} \end{matrix}$ 。本文中建立的叠前反演流程如图1所示。

	Figure Option View Download New Window
	图1 叠前反演流程

同样的, 如果有需要, 可将 $\begin{matrix} \sqrt{M_{2} / M_{1}} \end{matrix}$ , $\begin{matrix} \sqrt{μ_{2} / μ_{1}} \end{matrix}$ , $\begin{matrix} \sqrt{ρ_{2} / ρ_{1}} \end{matrix}$ 各自平方, 进而得到 $\begin{matrix} \frac{ΔM}{M} \end{matrix}$ , $\begin{matrix} \frac{Δμ}{μ} \end{matrix}$ 以及 $\begin{matrix} \frac{Δρ}{ρ} \end{matrix}$ , 最后进行低频补偿即可得到最终结果M、μ 和ρ 。

2 流体识别

流体因子是进行流体识别和含油气检测的重要依据, 虽然直接从反演中得到的纵横波模量都能对地下介质含流体区域有一定的响应, 例如在含流体区域纵波模量会降低而横波模量会升高, 但是纵横波模量的变化还与地下介质的岩性有着直接的关系, 因此直接使用纵横波模量来进行流体识别是不准确的。这里使用纵横波模量的流体因子来进行流体识别^[11]:

$\begin{matrix} f = M + cμ 。 (12) \end{matrix}$

其中:f为流体因子; c是调节参数, 为干燥岩石纵横波速度比的平方, 根据实际工区情况来确定最优的调节参数。

3 模型试算

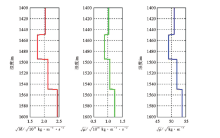
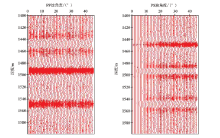
采用一个4层水平层状模型进行算法的测试, 相应的分界面分别处于1 450、1 495、1 550 m位置处。图2为理论层状模型; 图3为根据模型制作的合成角度为1° ~45° 的地震记录, 同时加入信噪比为2∶ 1的随机噪声; 图4为反演结果、低频模型和理论模型之间的对比。为了方便显示, 模型数据均为深度域表示。

由图4可以看到, 文中所建立的精确Zoeppritz方程的叠前纵横波模量反演方法相对于间接反演能够更精确的根据地震数据得到地下介质的纵横波模量和密度信息, 减小了间接反演所带来的累积误差, 同时也具有良好的抗噪性。

	Figure Option View Download New Window
	图2 理论层状模型

	Figure Option View Download New Window
	图3 信噪比为2∶ 1的合成地震记录

	Figure Option View Download New Window
	图4 直接反演结果、间接反演结果和实际模型的对比

4 实际资料测试

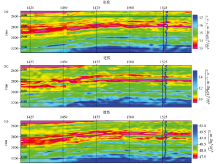
选取中国东部某工区实际地震数据进行测试。在进行叠前地震反演之前, 需要先对地震数据进行预处理, 包括对叠前道集进行部分叠加、叠前去噪、提取子波等。选取过井S1剖面进行实际资料的测试。图5为原始地震数据的叠后剖面; 图6为反演得到的纵波模量 $\begin{matrix} \sqrt{M} \end{matrix}$ 、横波模量 $\begin{matrix} \sqrt{μ} \end{matrix}$ 和密度 $\begin{matrix} \sqrt{ρ} \end{matrix}$ ; 图7 为根据反演得到的纵横波模量计算得到的流体因子。图中蓝色曲线为密度测井曲线左边为高值, 右边为低值。由于纵横波模量的物理定义, 二者分别与岩石的抗正应变能力和抗切应变能力相关, 而岩石抗应变能力分别与岩石的矿物成分和流体性质密不可分, 在含油气区域为低异常值, 可大致区分储层流体类型^[11]。S1井在2 700 ms附近为含油砂岩区域, 2 760 ms附近为含油砂砾岩区域。图6a显示反演得到的纵波模量未能很好的将两个储层中间的不含油气区域区分出来; 图6b显示横波模量能够很好地区分有利储层, 并且纵横波模量都能将图6c中2 800 ms以下的低密度区域进行有效地排除; 图7为结合纵横波模量得到的流体因子, 虽然同样能够很好地区分含油气区域。实际资料测试显示, 本文所建立的纵横波模量直接反演结果能够明显的区分岩性, 在实际应用时有着很好的应用价值。同时流体因子和横波模量相对纵波模量和密度反演结果能够将含油气区域很好地区分出来。

5 结论与认识

基于纵横波速度的精确Zoeppritz方程推导出纵横波模量的Zoeppritz方程。并通过求取方程对各个独立分量的一阶偏导将非线性的Zoeppritz方程进行线性化处理, 最后基于广义线性反演理论建立叠前纵横波模量直接反演方法, 提高了对地震资料的利用率, 使得大偏移距地震数据得以充分的利用。模型试算和实际资料测试表明, 本方法相对于间接反演, 减小了累积误差能够更精确的得到地下介质的纵横波模量, 并区分出有利储层。为叠前反演弹性参数提供了一种新的思路。文中所建立的叠前反演方法由于是基于广义线性反演理论, 不可避免的也会带来广义线性反演方法本身的缺点, 在后续的研究中需要结合其他反演方法来优化反演结果。

	Figure Option View Download New Window
	图5 叠后地震剖面

	Figure Option View Download New Window
	图6 叠前地震反演结果

a— 反演得到的纵波模量 $\begin{matrix} \sqrt{M} \end{matrix}$ ; b— 反演得到的横波模量 $\begin{matrix} \sqrt{μ} \end{matrix}$ ; c— 反演得到的密度 $\begin{matrix} \sqrt{ρ} \end{matrix}$

	Figure Option View Download New Window
	图7 流体因子剖面

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cooke D A, Schneider W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. [本文引用:1]
[2]	Macdonald C, Davis P M, Jackson D D. Inversion of reflection traveltimes and amplitudes[J]. Geophysics, 1987, 52(5): 606-617. [本文引用:1]
[3]	Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sand stone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique[J]. Geophysics, 1994, 59(9): 13621376. [本文引用:1]
[4]	Simmons Jr J L, Backus M M. Waveform-based AVO inversion and AVO prediction-error[J]. Geophysics, 1996, 61(6): 1575-1588. [本文引用:1]
[5]	Goodway B, Chen T W, Downton J. Improved AVO fluid detection and lithology discrimination using lamé petrophysical parameters;“λρ”, μρ, λμ fluid stack”, from P and S inversions[C]//Dallas, Texas: Expand ed Abstracts of 69^th SEG Meeting, 1997. [本文引用:2]
[6]	Buland A, Omre H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. [本文引用:1]
[7]	杨培杰, 印兴耀. 基于支持向量机的叠前地震反演方法[J]. 中国石油大学学报: 自然科学版, 2008, 32(1): 37-41. [本文引用:1]
[8]	杨培杰, 印兴耀. 非线性二次规划贝叶斯叠前反演[J]. 地球物理学报, 2008, 51(6): 1876-1882. [本文引用:1]
[9]	杨培杰, 王长江, 毕俊凤, 等. 可变点约束叠前流体因子直接提取方法[J]. 地球物理学报, 2015, 58(6): 2188-2200. [本文引用:1]
[10]	宗兆云, 印兴耀, 吴国忱. 拉梅参数直接反演技术在碳酸盐岩缝洞型储层流体检测中的应用[J]. 石油物探, 2011, 50(3): 241-246. [本文引用:1]
[11]	宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 2012, 55(1): 284-292. [本文引用:4]
[12]	宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. [本文引用:1]
[13]	张广智, 杜炳毅, 李海山, 等. 页岩气储层纵横波叠前联合反演方法[J]. 地球物理学报, 2014, 57(12): 4141-4149. [本文引用:1]
[14]	张丰麒. 纵波、转换波匹配与联合反演方法研究[D]. 青岛: 中国石油大学(华东), 2011. [本文引用:1]
[15]	周林, 李景叶, 陈小宏. 基于精确Zoeppritz方程的非线性AVO三参数反演[J]. 地球物理学报, 2016, 59(7): 2663-2673. [本文引用:1]
[16]	印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34. [本文引用:1]
[17]	Russell B H, Hedlin K, Hilterman F J, et al. Fluid-property discrimination with AVO: A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. [本文引用:1]
[18]	郝前勇. 岩石弹性参数反演与流体识别方法与应用[D]. 青岛: 中国石油大学(华东), 2013. [本文引用:1]
[19]	Ferguson R J, Margrave G F. A simple algorithm for band -limited impedance inversion[R]. CREWES Research Report, 1996. [本文引用:1]

1983

0.0

... Cooke^[1]最早建立了广义线性反演理论(GLI),并且应用于地震反演中 ...

1987

0.0

... Macdonald^[2]等对将广义线性反演方法针对Zoeppritz方程的线性程度进行了研究 ...

1994

0.0

... Fatti^[3]使用加权叠加法计算纵横波阻抗,第一次在反演中引入密度项而非使用Gardner公式进行拟合 ...

1996

0.0

... Simmons^[4]应用线性反演方法获得纵横波阻抗和密度,不足之处在于使用了Gardner公式 ...

1997

0.0

... Goodway等^[5]建立了基于拉梅常数的反演技术(LMR),实现了弹性参数的直接反演 ...

... 叠前地震反演的根本目的是流体识别和储层预测,如何有效地利用反演得到的弹性参数来分辨出地下介质中的流体一直以来都是人们研究的重点目标^[16],Goodway^[5]等人建立的LMR算法将拉梅常数作为流体异常识别因子,相对于纵横波速度具有较高的准确性 ...

2003

0.0

... Buland等^[6]研究了基于贝叶斯理论的线性反演方法 ...

2008

0.0

2008

0.0

2015

0.0

2011

0.0

2012

0.0

... Russell等^[17]建立了Russell流体因子,该流体因子基于Biot-Gassmann理论,并假设孔隙中为饱和流体,忽略了孔隙中流体在非饱和的情况,宗兆云^[11]对Russell流体因子进行了改进,将流体因子由纵横波阻抗和密度的函数改进为纵横波模量的函数,郝前勇^[18]研究了多弹性参数和流体因子之间的定量关系,并结合地震、测井和地质信息实现综合的流体识别和储层预测 ...

... 在理想介质中,纵横波速度和纵横波模量之间的关系为^[11]: ...

... 这里使用纵横波模量的流体因子来进行流体识别^[11]: ...

... 由于纵横波模量的物理定义,二者分别与岩石的抗正应变能力和抗切应变能力相关,而岩石抗应变能力分别与岩石的矿物成分和流体性质密不可分,在含油气区域为低异常值,可大致区分储层流体类型^[11] ...

2012

0.0

2014

0.0

... 张广智^[13]针对页岩气建立了基于弹性阻抗反演方法直接求取杨氏模量和密度的乘积以及泊松比的方法 ...

0.0

... 张丰麒^[14]基于广义线性反演理论建立了纵横波联合反演纵波速度、横波速度和密度的方法,该方法直接使用Zoeppritz方程进行反射系数的求取,有效避免了由于使用近似式导致的大角度地震数据无法被有效利用的缺陷 ...

2016

0.0

... 周林等^[15]利用精确Zoeppritz方程进行了AVO三参反演,并验证了大角度地震数据能够有效提高反演精度,尤其是对于密度反演结果 ...

2014

0.0

2003

0.0

1996

0.0

... 反射系数结合低频数据进行低频补偿^[19]即可得到最终的反演结果 M、 μ和 ρ ...