作者简介: 吴吉忠(1985-),博士,2008年本科毕业于中国海洋大学勘查技术与工程专业,2014年博士毕业于中国科学院地质与地球物理研究
提出的角度域叠前时间偏移方法,能够在偏移成像过程中直接生成倾角域成像道集,在倾角成像道集上确定真地层倾角与倾角成像区,获得的最终叠加剖面在保证构造正确成像的同时避免了过大偏移孔径带来偏移噪声的弊端,提高了剖面的信噪比。应用本文方法在南堡凹陷马头营凸起地区取得了较好的应用效果,表明该方法对于信噪比较低、偏移噪声大的地区具有较大的工业应用价值。
This paper proposes an approach to prestack time migration in dip angle domain,which can produce common dip-angle imaging gathers directly.Dip angles and imaging area can be determined on these gathers.The final imaging profile is right without migration noise,which could improve signal-to-noise ratio.This scheme was applied to real data of the Matouying structure in Napu sag,and the good results demonstrate that the approach to prestack time migration in dip angle domain has broad application prospects for low signal-to-noise ratio and big noise area.
目前工业界普遍采用共偏移距域叠前时间偏移进行叠前成像处理, 实现了CMP道集(共中心点道集)到CRP道集(共反射点道集)的转换, 该类方法是一种成像与速度分析的重要手段, 对于一类倾角、断层较为复杂但横向速度变化不是很剧烈的构造有较好的成像, 且具有较高的计算效率, 速度模型可通过速度扫描的方式获取。偏移孔径是影响叠前时间偏移成像的重要因素, 较好的偏移孔径对压制偏移噪声和减少偏移计算量具有重要作用, 较小的偏移孔径虽然可以减少偏移计算量, 但存在着陡倾角构造无法正确成像的风险, 过大的偏移孔径在带来偏移噪声的同时又增加了额外的计算量。在实际生产中, 受限于偏移算法的实现方式, 在一个偏移作业中总是选取一个统一的偏移孔径, 为了保证所有构造的成像, 偏移孔径往往都要偏大, 这不可避免的导致偏移噪声存在于CRP道集上, 而常规的CRP道集切除只是对动校与拉伸畸变进行了处理, 偏移噪声的存在导致了最终叠加剖面信噪比的降低。
通常, 偏移孔径的范围是根据地层倾角事先给定的, 但在成像前获取准确的地层倾角是十分困难的。基于地层倾角与偏移孔径的关系, 很多学者利用地层倾角来限制偏移孔径, 进而达到提高成像信噪比的目的, 刘合年等通过地层倾角确定用于成像的叠前数据范围的方式来实现偏移孔径的优化[1], Audebert等通过出射角与剖面上反射层倾角约束的方式来实现[2], Alexander Klokov等在深度域通过倾角成像道集部分叠加来达到偏移孔径最优选取的目的[3]。关于地层倾角的求取, 可以在波动理论框架下利用波场局部方向分解得到[4], 或者在射线理论框架下采用计算旅行时的空间梯度得到[5], 也可以采用倾角扫描的方式获取地下的地层倾角
笔者提出的角度域叠前时间偏移方法, 可以直接生成倾角域成像道集, 在倾角成像道集上确定真地层倾角与倾角成像区, 获得的最终叠加剖面在保证构造正确成像的同时避免了过大偏移孔径带来偏移噪声的弊端, 提高了剖面的信噪比。该方法包含两步操作, 第一步是生成共反射点位置对应的倾角成像道集, 第二步是在倾角成像道集上确定倾角成像区, 并水平叠加得到最终偏移成像剖面。该方法通过倾角成像道集的最优部分叠加, 达到了偏移孔径优化的效果, 避免了叠前成像过程中孔径不易求准的弊端, 也解决了偏移孔径过大带来的偏移噪声导致叠加剖面信噪比降低的问题, 通过在渤海湾盆地南堡凹陷复杂构造成像中的应用, 证明了该方法的有效性。
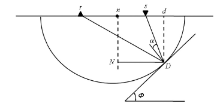
如图1所示, s, r分别是炮点与激发点, n为s与r的中点, 设定输入地震数据的半偏移距为h, ϕ 为t深度处的地层倾角, D为t深度处最远成像道对应的成像点, d为成像点D在地面的投影, 过点n作垂线段与过D的水平线段相交于点N, 则可以推导出:
其中:t是成像点对应的时间深度, 为单程旅行时; vrms为叠加速度; α 是激发点出射的地震波在成像点处的入射角; x为点N与点D之间的水平距离, 也是时间深度t处地层倾角ϕ 对应的偏移孔径。对式(1)、(2)进行联立求解, 可得:
由式(3)可以看出, 任一时间深度的偏移孔径在速度与偏移距保持不变的情况下, 取决于成像构造的地层倾角, 地层倾角越大, 所需要的偏移孔径越大。
1.2.1 地层倾角的计算
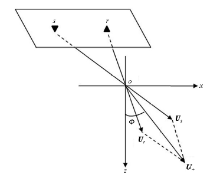
生成倾角成像道集首先需要计算反射界面的倾角, 可以在波动理论框架下利用波场局部方向分解得到[4], 也可以在射线理论框架下采用计算旅行时的空间梯度得到[5]。如图2所示, 在二维情况下, 成像空间散射点O处的波传播方向特征可以用入射慢度矢量Us和散射慢度矢量Ur共同描述[9]。U+为入射与散射慢度矢量之和, 称之为照明矢量。U+与z轴夹角就是照明倾角ϕ , 它与反射界面倾角是等值的。s与r分别代表激发点与接收点。通过计算得到旅行时场的梯度方向, 进而可以得到激发点与接收点入射方向的Us与Ur, 则可得出:
其中τ s与τ r分别为激发点和接收点的旅行时场, 利用Us与Ur可以得到反射界面倾角:
1.2.2 叠前时间偏移与倾角成像道集
基于单程波方程与稳相点理论, 并参照深度偏移相移方法研究叠前时间偏移中走时及振幅的计算[10, 11], 若设激发震源是一个时间脉冲, 可以得到地层倾角ϕ 时叠前时间偏移成像结果:
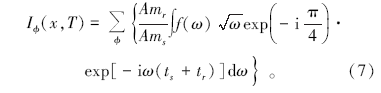
其中:ϕ 是地层倾角值, x是成像点对应的地表位置, T是成像点时间深度, f(ω )是单道地震数据在频率— 波数域的表达, ω 是圆频率, i是虚数单位, Ams与ts是炮点至成像点的幅值和走时, Amr和tr是求得的检波点至成像点的幅值和走时, 在成像过程中利用文中提出的方法计算地层倾角值, 将成像结果按倾角排列、部分叠加, 最终生成倾角成像道集[12]。
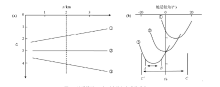
在倾角成像道集中, 横轴代表地层倾角值, 纵轴代表时间深度, 对于任一成像点而言, 最终的成像结果来源于真地层倾角, 其他角度的像是没有干涉掉的噪声[3, 5]。在速度正确的情况下, 反射波的同相轴形态为拟双曲线形状, 并且顶点对应的角度即是真地层倾角, 利用此特点, 可以在倾角成像道集上确定出地下反射层的真地层倾角, 但是在实际应用中由于数据的不规则及速度存在误差, 最终的成像结果不仅仅来源于倾角成像道集上真地层倾角位置, 真地层倾角附近的部分也对成像结果起到了贡献, 文中把倾角成像道集上决定最终成像结果的真地层倾角及其附近的部分称之为倾角成像区, 对于任一成像点而言, 它的倾角成像区可表达为[ϕ -η 1, ϕ +η 2], 其中ϕ 为真地层倾角值, ϕ -η 1为倾角成像区起始倾角值, ϕ +η 2为倾角成像区终止倾角值, η 1与η 2分别为倾角变量, 当ϕ -η 1与ϕ +η 2选取恰当的时候, 成像点处的成像结果趋于稳定并达到极大值[13, 14], 利于此特点可以确定倾角成像区的范围。为了阐明文中确定的倾角成像区能够起到对偏移孔径进行优化的作用, 用图3a所示的地质模型数据进行了说明。该地质模型含有3层界面, ①与③代表2个倾斜层, ②代表1个水平层, 图3b代表该地质模型数据对应的倾角成像道集, 其中①、②与③分别代表3个同相轴, 与图3a中的地层编号一一对应。下面以地层③为例, 在倾角成像道集上, 拟双曲线的顶点处对应的角度便是真实的地层倾角, 利用上文叙述的方法可以确定倾角成像区为[A, B], A与B分别是倾角成像区的起始角度与终止角度, 常规叠前时间偏移的偏移孔径映射到倾角成像道集上也有类似的成像区带, 并且成像区带的起始角度与终止角度分别位于倾角成像道集0° 分界线的两侧, 起始角度与终止角度大小一致, 均为常规叠前时间偏移给定的地层倾角值, 在图3b上分别记为C'与C, 由于该角度要比真实的偏大, 于是C'位于真实地层倾角的左侧, 在图3b上[C', C]部分便是常规叠前时间对应的偏移孔径。通过对比可以看出, 最终成像结果对于本文方法而言来源于[A, B]部分, 而对于常规方法而言则来源于[C', C]部分, 常规方法为了实现构造的正确成像, 将大量的偏移噪声带入了最终成像结果, 降低了地震数据的成像品质, 而本文方法仅利用[A, B]部分进行成像, 在保证构造正确成像的同时, 避免了大量的偏移噪声进入成像结果, 达到了优化叠前偏移孔径的效果[15]。
1) 利用偏移速度场, 对叠前数据在每个成像点位置求取地震波走时、偏移幅值与倾角大小, 并按照倾角排列, 部分叠加, 得到共反射点位置的倾角道集;
2) 针对剖面上若干共反射点位置处的倾角道集, 根据双曲顶点的位置拾取出真地层倾角, 并确定出倾角成像区;
3) 利用已确定的若干共反射点位置的倾角道集对应的倾角成像区, 通过插值延拓的方式确定其余共反射点位置的倾角道集对应的倾角成像区;
4) 将倾角成像区内的地震幅值进行边界衰减并叠加, 得到最终的地震成像剖面。
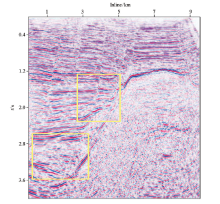
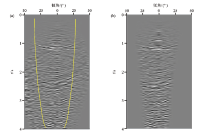
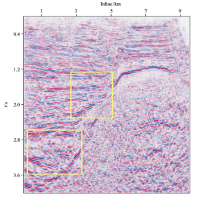
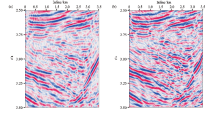
文中选取渤海湾盆地南堡凹陷马头营凸起地震数据进行了数值试验, 为了进行方法对比, 先用共偏移距域叠前时间偏移对该数据进行偏移成像, 得到了图4a所示的CRP道集, 然后对中远偏移距动校拉伸造成的畸变进行切除, 得到了图4b所示的道集, 在偏移过程中, 为了保证构造的正确成像, 偏移孔径都要比实际需求偏大, 过大偏移孔径带来的偏移噪声存在于CRP道集上, 从近偏移距道集到中远偏移距道集都有分布, 常规的道集切除办法无法解决CRP道集存在偏移噪声的问题, 后期的去噪处理虽然可以对偏移噪声进行压制, 但从保幅性角度看, 后期去噪对有效信号有一定损害。将所有切除后的CRP道集水平叠加起来就得到了最终的叠加剖面, 如图5所示。应用本文提出的角度域叠前时间偏移方法, 按照文中所述的流程, 得到了倾角域成像道集, 如图6a所示, 针对剖面上若干共反射点位置处的倾角道集, 根据双曲顶点的位置拾取出真地层倾角, 并确定出倾角成像区的范围, 图6a上左右两条黄色折线包围的部分便是某共反射点位置对应的倾角成像区, 将倾角成像区以外的干扰信号切除, 得到了如图6b所示的只保留有效信号的倾角成像道集。图7是利用本文方法得到最终的地震成像剖面。为了便于细节对比, 在图5与图7上选取了中浅层与深层两个时窗(黄色矩形框)进行局部对比, 图8展示的是中浅层时窗局部细节对比, 其中图8a是常规叠前时间偏移剖面, 图8b是本文方法得到的剖面, 通过对比可以看出, 图8b信噪比有所提高, 同相轴变得更加光滑、连续性更好, 断点收敛更加干脆, 地层之间接触关系也更加明确, 这表明本文提出的角度域叠前时间偏移方法在控制偏移噪声方面较传统方法有一定优势, 对偏移孔径过大引起的偏移噪声压制较好。
与中浅层相比, 深层构造常规叠前时间偏移成像需要更大的偏移孔径, 偏移噪声也更加严重。图9展示的是深层时窗细节对比, 图9a是常规叠前时间偏移剖面, 信噪比较低, 同相轴“ 毛刺” 较多, 不利于后期的构造解释与储层预测; 图9b是本文方法得到的剖面, 信噪比有显著提高, 同相轴连续性更好, 波组形态也更趋于真实自然, 这表明角度域叠前时间偏移方法对深部构造成像的信噪比改善有一定作用。
文中提出的角度域叠前时间偏移方法, 可以直接生成倾角域成像道集, 通过倾角成像道集的最优部分叠加, 达到了偏移孔径优化的效果, 避免了叠前成像过程中孔径不易求取的弊端, 也解决了偏移孔径过大带来的偏移噪声导致叠加剖面信噪比降低的问题。由南堡凹陷马头营凸起实际地震资料的应用可以看出, 应用本文方法后剖面信噪比得到了一定改善, 成像质量得到提高。本文方法对于信噪比较低、偏移噪声大的地区有着广阔的应用前景。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|