引用本文
董莉, 江沸菠, 戴前伟, 傅宇航. 基于支持向量机回归的电阻率成像反演[J]. 物探与化探, 2017,41(3): 505-512.
DONG Li, JIANG Fei-Bo, DAI Qian-Wei, FU Yu-Hang. Electrical resistivity imaging inversion based on support vector regression[J]. Geophysical and Geochemical Exploration, 2017,41(3): 505-512.
Doi:10.11720/wtyht.2017.3.16  
Permissions
Copyright©2017, 物探与化探编辑部
© 《物探与化探》编辑部
基于支持向量机回归的电阻率成像反演
董莉1,2, 江沸菠2,3, 戴前伟2, 傅宇航4
1.湖南涉外经济学院 信息科学与工程学院,湖南 长沙 410205
2.中南大学 地球科学与信息物理学院,湖南 长沙 410083
3.湖南师范大学 物理与信息科学学院,湖南 长沙 410081
4.湖南送变电勘察设计咨询有限公司, 湖南 长沙 410114
通讯作者: 江沸菠(1982-),男,博士,博士后,讲师;从事电磁法非线性反演和人工智能工程应用研究等工作。Email:jiangfeibo@126.com

作者简介: 董莉(1982-),女,博士,讲师,主要研究方向为电磁法非线性反演。Email:48757467@qq.com

收稿日期: 2016-05-20
基金: 国家自然科学基金资助项目(41604117、41374118); 中国博士后科学基金资助项目(2015M580700); 湖南省教育厅优秀青年基金资助项目(15B138); 湖南省科技创新计划资助项目(2016JJ3086)
摘要

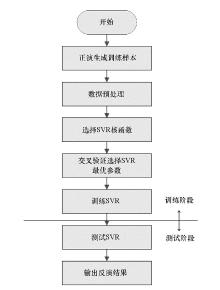
以电阻率成像为应用背景,研究了在有限学习样本下,支持向量机回归在电法反演中的建模方法,对反演建模时样本划分、数据预处理、反演流程、评估指标等关键技术进行了分析,给出了一种基于交叉验证(CV)的支持向量机参数寻优方法;通过比较RBF核函数在不同的参数 ε下对反演结果的影响,建立了优化的电阻率成像SVR反演模型。

关键词: 电阻率成像; 支持向量机回归; 反演
中图分类号:P631 文献标志码:A 文章编号:1000-8918(2017)03-0505-08
Electrical resistivity imaging inversion based on support vector regression
DONG Li1,2, JIANG Fei-Bo2,3, DAI Qian-Wei2, FU Yu-Hang4
1. Department of Information Science and Engineering, Hunan International Economics University, Changsha 410205, China
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China
3. College of Physics and Information Science, Hunan Normal University, Changsha 410081, China
4. Hunan Power Transmission and Distribution Survey and Design Consulting Co., Ltd., Changsha 410114, China
Abstract

Support Vector Regression is a Learning Machine based on statistic learning theory. It has better performance of generalization and fitting precision than traditional neural network inversion under the condition of small samples learning. Under the application background of electrical resistivity imaging, SVR inversion method based on limited learning samples was studied in this paper. The key issues of sample division and data preprocessing, inversion flow and evaluation indicators were analyzed. A multi-parameter optimization method based on cross validation was presented. The optimized SVR inversion model by comparing the influence of RBF kernel functions with different ε values with the inversion results was established. Data simulation and model inversion show that the proposed inversion method has better inversion accuracy and imaging quality than traditional least squares inversion and RBFNN inversion, and is equivalent to BPNN, but it has disadvantage of only one output dimension.

Keyword: electrical resistivity imaging; support vector regression; inversion
0 引言

电阻率成像(electrical resistivity imaging, ERI)技术是一种地球物理勘探方法, 它利用多道阵列电极系测量系统, 通过在地表或井— 地布设阵列电极系获取地下电阻率信息, 并利用正反演方法以重建地下电阻率图像, 来揭示地下介质的电性结构。目前ERI常见的解释方法有α 中心法[1]、最小二乘法[2]、佐迪法[3]、积分法[4]等。传统的线性反演方法依赖于初始模型的选择, 易陷入局部极值和求解雅克比矩阵困难等问题, 而电阻率成像技术是一种非线性反演的方法, 现在越来越受到人们的关注。

支持向量机是近年来迅速发展的一种通用机器学习方法, 它具有以下优点:①优化目标基于结构风险最小化原则, 保证了良好的泛化能力; ②建立在统计学习理论基础之上, 研究的是小样本时的最优解; ③可将求解问题转化为凸优化问题, 从而避免了陷入局部极小的缺陷; ④具有严格的理论和数学基础, 避免了类似神经网络实现中的经验成分。研究表明, 支持向量机技术具有较强的非线性建模和反演能力。

笔者采用支持向量机回归技术进行电阻率成像的反演建模, 研究了反演建模时样本划分、数据预处理、反演流程、评估指标等关键技术; 比较了径向基函数 (radial basis function, RBF)在不同的不敏感损失函数ε 下对反演结果的影响, 给出了一种基于交叉验证方式的支持向量机参数寻优方法, 建立了优化的支持向量机回归电阻率成像反演模型。

1 支持向量机回归

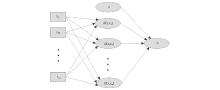
支持向量机回归(support vector regression, SVR)是支持向量在函数回归领域内的应用, 对于给定的训练样本集{(x1, z1), (x2, z2), …, (xl, zl)}, xi∈ Rn为特征向量, zi∈ R1为输出向量。支持向量机的体系结构如图1所示, 其中输入(xi, 1, xi, 2, …, xi, n)T为训练样本xi的维度分量, 中间层由m个支持向量的非线性变换构成, 输出一般为中间层节点的线性组合[14]。

图1 支持向量机的基本结构

对于线性回归函数:

f(x)=w·Φ(x)+b, (1)

式(1)中, w为权向量, b为阈值, Φ (x)为输入样本x的非线性映射。假设所有训练样本(xi, zi)均可以在精度ε 下用线性函数拟合, 则回归估计问题可转化为以下约束优化问题:

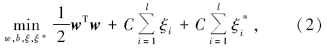
其约束条件为:

wTΦ(xi)+b-zi≤ε+ξi; zi-wTΦ(xi)-b≤ε+ξi* ; ξi≥0, i=1, …, l; ξi* ≥0, i=1, …, l。

式(2)中:ξ i、 ξi* 为松弛因子, 最小化 12wTw项使函数更为平坦, 从而提高泛化能力; 最小化 项则用来减少拟合误差, 常数C用来平衡回归函数f的平坦程度和偏差大于ε 样本点的个数。

为求解以上约束优化问题, 支持向量机根据对偶原理, 通过引入拉格朗日函数将其转化为二次规划问题:

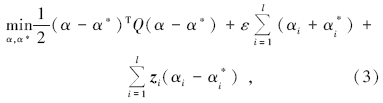
其约束条件为:

eT(α-α* )=0; 0≤αi, αi* ≤C, i=1, 2, …, l。

式(3)中:Qij=K(xi, xj)=Φ (xi)TΦ (xj)为核函数, 为满足Mercer条件的任意对称函数, 相当于Hilbert空间的内积。

通过求解以上二次规划问题, 可得最优解α =[α 1, α 2, …, α l]和α * =[ α1* , α2* , …, αl* ], 则有

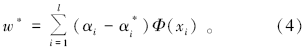
然后, 结合Karush-Kuhn-Tucker条件可得偏置b* :

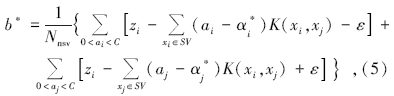
式中Nnsv为支持向量个数。最后得到拟合后的系统:

2 电阻率成像SVR反演建模

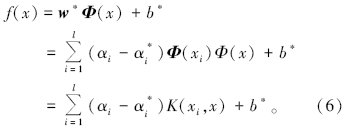
针对二维电阻率成像技术进行支持向量机回归非线性反演的理论研究, 样本的正演模型参数设置如下:采用温纳-斯伦贝格装置, 测量电极为41个, 电极距为1 m, 一条测线上共采集14层350个数据点。正演方法采用有限体积法。

2.1 样本划分

使用视电阻率的水平位置、垂直位置和视电阻率值为输入节点, 对应位置的真电阻率值为输出节点, 将每次测量的所有数据点设为一个数据集进行训练[9]。根据支持向量机工作原理可知, 样本的输入维度为3, 支持向量机模型的输出维度为1, 代表对应位置的真电阻率。

支持向量机的训练数据通过在均匀介质背景下改变高、低阻异常体的位置和形态来获得, 共获取38组训练数据集。为测试支持向量机的泛化性能, 同时提供2组测试数据集, 测试数据均未参加网络训练。图2列出了部分用于训练的样本模型。

图2 用于SVR训练的部分样本模型

2.2 数据预处理

由于训练样本中不同维度所代表的物理含义不同, 其数值范围往往会存在较大的差异, 这将影响学习机器在学习过程中的性能。为保证样本中不同输入维度在数值上的一致性, 对样本进行预处理, 其标准化处理的公式为[16]

xi=λ1+(λ2-λ1)yi-yiminyimax-yimin, (7)

对应的反定标公式为

yi=xi-λ1λ2-λ1(yimax-yimin)+yimin, (8)

式中:yi为反定标数据; xi为对应的标准化数据; λ 1和λ 2为上下边界, 本文设置为0和1; yimin和 yimax为原始数据数据的最小值、最大值。通过预处理, 可以消除样本中各个维度数据间的数量级差别, 消除训练过程中的振荡, 提高支持向量机的学习能力。

2.3 SVR参数寻优

对于非线性问题, 支持向量机利用非线性映射函数将样本映射到高维线性空间, 然后在此空间构造线性分类器或回归函数。样本在高维空间的点积运算可以用低维输入空间的核函数来实现, 而核函数的类型和参数γ 间接决定了样本在高维线性空间的分布, 从而影响了SVR的性能; 同时, 误差惩罚参数C是调整模型复杂性和经验风险的参数, 对SVR的性能有较大的影响。最后构造SVR时, 最常用的损失函数是Vapnik[17]提出的ε 不敏感损失函数:

Lε[f(xi)-zi]=0, |f(xi)-zi< ε|f(xi)-zi-ε, |f(xi)-zi> ε(9)

式(9)中, 参数ε 的选择是影响 SVR 性能的关键因素之一[18]。为构造优化的SVR反演模型, 需要对核函数的类型以及参数C、γ 和ε 进行优选, 考虑到核函数对支持向量机的直接影响, 首先对核函数的类型进行分析。在支持向量机中常用的核函数包括以下几种:

1) 线性核函数:

K(x, xi)=xTxi。(10)

2) 多项式核函数:

K(x, xi)=(γxTxi+r)p, γ> 0。(11)

3) RBF核函数:

K(x, xi)=exp(-γ‖x-xi‖2), γ> 0。(12)

4) Sigmoid核函数:

K(x, xi)=tanh(γxTxi+r)。(13)

其中, RBF核函数在处理复杂的非线性回归问题时更具有优势[18], 考虑到电阻率成像反演是一类复杂的非线性问题, 主要评估RBF核函数在不同SVR参数下对反演结果的影响, 从而实现对SVR参数的寻优。

在确定了待评估的核函数类型后, 选择惩罚参数C和核函数参数γ 的方法是让C和γ 在一定范围内进行取值, 在不同的C和γ 参数下将训练集利用交叉验证(cross validation, CV)的方式进行训练, 得到特定参数下训练集的训练精度, 最终取得使训练集训练误差达到最低的那一组C和γ 作为支持向量机回归的最佳参数。

表1给出了不同参数下支持向量机回归反演的K-CV训练误差、K-CV测试误差和参数寻优时间。其中参数寻优时间的计算环境如下:CPU为Core i5-2450, 内存为4GB, 操作系统为Windows 8.1。

表1 不同参数下支持向量机回归反演的性能比较

由表1可知, 采用RBF核函数的SVR, 其训练误差和测试误差均较低, 进一步说明了采用RBF核函数的SVR更加适合于进行电阻率成像反演的建模。同时可以看到, 随着取值的减小, 采用RBF核函数的SVR, 获得了更佳的训练精度和测试精度, 显示了SVR优良的泛化能力; 但是, 当ε 取值为0.01和0.001时, 参数C和γ 的取值并没有明显的变化, 说明当ε 取值低于0.01时, SVR性能的改进主要是通过优化内部结构获得的, 与参数的寻优无关, 同时其计算时间显著提高, 但训练精度和测试精度并没有明显的改进。因此, 综合考虑反演的计算效率和精度, 在K-CV方法下的最佳的支持向量机回归参数分别为:惩罚参数C=2.8284、核函数参数γ =45.2548、核函数类型为RBF核函数、ε 取值为 0.01。

2.4 反演流程

通过以上分析, 使用SVR反演电阻率成像数据的流程如图3所示, 基本步骤如下:

图3 基于SVR的电阻率成像反演流程

1)使用有限体积法正演产生训练与测试数据集, 并进行数据预处理, 以保证样本中不同输入维度在数值上的一致性;

2)在当前的训练与测试环境下, 通过K-CV方法对SVR的参数进行优选, 其主要包括核函数类型的选择, ε 、C和γ 参数的寻优;

3)输入训练数据集, 对选定参数的SVR进行训练, 并保存训练后的支持向量机;

4)输入测试数据集, 使用构造好的SVR进行反演, 输出并评估反演结果。

3 数据仿真与模型反演
3.1 评价指标

为了评估使用的支持向量机的反演性能, 采用算法执行所需要的CPU时间来衡量算法的计算速度, 测量CPU时间的计算环境如前所述。同时采用均方误差(mean square error, MSE)和决定系数(determination coefficient, R2)来衡量各种学习机器的学习性能, 其相关定义如下:

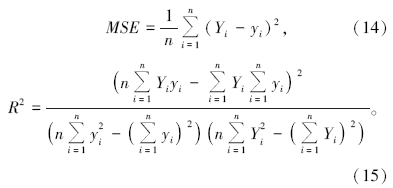
式中:yi为第i个训练数据的预测值, Yi为第i个训练数据的理论值, n为训练数据的数量。以上指标中MSE代表预测误差, 其值越小, 表示学习机器的预测误差越小; R2代表预测值与测量值之间的相关度, 其值越大, 表示两种数据间存在着越明显的线性相关性。

3.2 数值仿真比较

为了验证上述建模方式的反演性能, 将SVR与神经网络的反演结果进行比较, 其训练和测试数据如前文2.1节所述。神经网络选用3层的BP神经网络和RBF神经网络, 3种机器学习模型的参数设置如表2。

表2 不同学习机器的参数设置

不同学习机器在本文的实验条件下经过训练和测试, 其训练和测试均方误差和决定系数以及训练时间如表3所示。由表3可知, 3种学习机器在训练阶段均能够有效收敛, 但是SVR算法的训练误差和测试误差均较BP神经网络更优。在本文的反演中, 为达到设定的训练精度, RBF神经网络最终的隐节点数目为450。相对于BPNN和RBFNN来说, SVR具有更优的决定系数值R2, 表明其反演的结果与理论数据更加接近, 误差波动小, 具有较好的泛化性能和较高的稳定性。

表3 不同学习机器的性能比较
3.3 模型反演比较

为了验证支持向量机回归在电阻率成像反演中的可行性, 在两个不同的异常体模型下, 分别采用不同的反演方法对反演结果进行对比。

用于验证的模型1为一个不规则的高阻异常体。模型1的基本参数如下:采用温纳-斯伦贝格装置, 每排41个电极, 14层电阻率数据, 电极距为1.0 m, 围岩电阻率为100 Ω · m, 高阻异常体电阻率为500 Ω · m, 顶部埋深为1 m。用该模型的正演视电阻率作为支持向量机回归的输入, 对模型进行反演测试, 支持向量机和RES2DINV软件输出的反演结果如图4所示。

图4 模型1的模型示意及不同方法的反演结果

从反演的结果可以看出, 支持向量机回归反演算法和传统的最小二乘法均能够较为准确地反映高阻异常体的形态、位置和电阻率, 但支持向量机回归反演算法的结果更加精确, 重构异常体的形状和轮廓更加清晰, 其反演结果总体优于最小二乘法的反演结果。

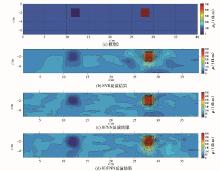
用于验证的模型2为高低异常体的组合模型, 用来检验支持向量机回归与神经网络反演结果之间的差异。模型2的基本参数如下:采用温纳-斯伦贝格装置, 每排含41个电极, 14层电阻率数据, 电极距为1.0 m, 围岩电阻率为100 Ω · m, 低阻异常体大小为2 m× 2 m, 电阻率为10 Ω · m, 其顶部埋深为 1 m; 高阻异常体的大小为2 m× 2 m, 电阻率为 500 Ω · m, 其顶部埋深为1 m。用该模型的正演视电阻率作为支持向量机和神经网络的输入, 对学习机器进行反演测试, 各学习机器输出的反演结果如图5所示。

图5 模型2的模型示意及不同方法的反演结果

从反演结果来看, 3种学习机器均能够较为准确地反演出异常体的存在和位置, 相对而言, SVR的反演结果在高阻异常体形态的重构上优于RBFNN的反演结果, 与BPNN的反演结果相当。总的来说, 3种学习机器对于高阻异常体的重构较好, 对于低阻异常体在重构上均存在不同程度的失真, 这是因为高阻异常体与背景电阻率的差异较大, 低阻异常体与背景电阻率的差异相对较小, 所以基于机器学习类的反演方法在本文的样本构造方法下, 更加适合进行高对比度区域的反演。

4 结论

采用向量机回归技术来实现二维电阻率成像的非线性反演建模, 研究了建模过程中样本划分、数据预处理、支持向量机参数寻优等关键性问题, 并给出了优化后的支持向量机回归反演模型。数值仿真与模型反演的结果表明:

1)通过合理的设计支持向量机, 能够使得训练后的支持向量机基本准确的反映电阻率成像反演中视电阻率与模型参数间的非线性映射关系, 取得较好的反演结果;

2)核函数类型对电阻率成像反演的结果有较大的影响, 在本文中选用RBF核函数进行反演;

3)通过交叉验证的方式选择惩罚参数C和核函数参数, 能够有效保证SVR的泛化能力, 在小样本的实验条件下提高学习机器的反演性能;

4)在样本构造方法下, SVM的反演结果与神经网络的反演结果基本相当, 不同样本数量下两者的性能差异还有待进一步深入研究。

总之, 研究表明支持向量机回归在电阻率成像反演中是可行的, 为电阻率成像反演问题的解决提供了一些可借鉴的经验。但是, 标准支持向量机回归的输出维度较低, 使得在样本构造中不得不采用基于单点的样本构造方法, 该方法在样本构造时, 在一定程度上分割了相邻视电阻率间的相互关系, 无法充分反映视电阻率是电场作用范围内地下电性不均匀体的综合反映这一视电阻率的本质特征。因此, 对于复杂的电阻率成像问题, 选择改进的多输出支持向量机进行反演建模, 可以获得更精确的反演结果。

The authors have declared that no competing interests exist.

参考文献
[1] Shima H. 2-D and 3-D resistivity image reconstruction using crosshole data[J]. Geophysics, 1992, 57(10): 1270-1281. [本文引用:1]
[2] Loke M H, Barker R D. Least-squares deconvolution of apparent resistivity pseudosections[J]. Geophysics, 1995, 60(6): 1682-1690. [本文引用:1]
[3] Zohdy A A R. A new method for the automatic interpretation of Schlumbeger and Wenner sounding curves[J]. Geophysics, 1989, 54(2): 245-253. [本文引用:1]
[4] Lesur V, Cuer M, Straub A. 2-D and 3-D interpretation of electrical tomography measurements, Part2: The inverse problem[J]. Geophysics, 1999, 64(2): 396-402. [本文引用:1]
[5] Singh U K, Tiwari R K, Singh S B. Neural network modeling and prediction of resistivity structures using VES Schlumberger data over a geothermal area[J]. Computers & Geosciences, 2013, 52: 246-257. [本文引用:1]
[6] Singh U K, Tiwari R K, Singh S B. One-dimensional inversion of geo-electrical resistivity sounding data using artificial neural networks—a case study[J]. Computers & geosciences, 2005, 31(1): 99-108. [本文引用:1]
[7] El-Qady G, Ushijima K. Inversion of DC resistivity data using neural networks[J]. Geophysical prospecting, 2001, 49(4): 417-430. [本文引用:1]
[8] 徐海浪, 吴小平. 电阻率二维神经网络反演[J]. 地球物理学报, 2006, 49(2): 584-589. [本文引用:1]
[9] Neyamadpour A, Taib S, Abdullah W A T W. Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions: a MATLAB application[J]. Computers & Geosciences, 2009, 35(11): 2268-2274. [本文引用:1]
[10] Zhang L Y, Liu H F. The application of ABP method in high-density resistivity method inversion[J]. Chinese Journal of Geophysics. (in Chinese), 2011, 54(1): 22764-23371. [本文引用:1]
[11] Ho T L. 3-D inversion of borehole-to-surface electrical data using a back-propagation neural network[J]. Journal of Applied Geophysics, 2009, 68(4): 489-499. [本文引用:1]
[12] Neyamadpour A, Wan Abdullah W A T W, Taib S, et al. 3D inversion of DC data using artificial neural networks[J]. Studia Geophysica et Geodaetica, 2010, 54(3): 465-485. [本文引用:1]
[13] 戴前伟, 江沸菠, 董莉. 基于汉南-奎因信息准则的电阻率层析成像径向基神经网络反演[J]. 地球物理学报, 2014, 57(4): 1335-1344. [本文引用:1]
[14] 史峰, 王小川, 郁磊. Matlab神经网络案例分析[M]. 北京: 北京航空航天大学出版社, 2010. [本文引用:1]
[15] Pidlisecky A, Knight R. FW2_5D: A MATLAB 2. 5-D electrical resistivity modeling code[J]. Computers & Geosciences, 2008, 34(12): 1645-1654. [本文引用:1]
[16] Wang H S, Wang Y N, Wang Y C. Cost estimation of plastic injection molding parts through integration of PSO and BP neural network[J]. Expert Systems with Applications, 2013, 40(2): 418-428. [本文引用:1]
[17] Vapnik V. Vapnik. Statistical learning theory[ M]. New York, NY: Wiley, New York, NY, 1998. [本文引用:1]
[18] 闫国华, 朱永生. 支持向量机回归的参数选择方法[J]. 计算机工程, 2009, 35(14): 218-220. [本文引用:2]
[19] 邴萍萍, 曹思远, 路交通. 基于支持向量机的非线性AVO反演[J]. 地球物理学报, 2012, 55(3): 1025-1032. [本文引用:1]
[20] 易世华, 刘代志, 何元磊, 等. 变化地磁场预测的支持向量机建模[J]. 地球物理学报, 2013, 56(1): 127-135. [本文引用:1]
[21] 江沸菠, 戴前伟, 董莉. 基于主成分—正则化极限学习机的超高密度电法非线性反演[J]. 地球物理学报, 2015, 58(9): 3356-3369. [本文引用:1]