假设地电体是电阻率为ρ 的均匀半空间(图1), 在地表A(0, 0, 0)点增加点电源, 强度为I, 地下任意点P(x, y, z)的电位U_P值计算公式为

UP=Iρ2πx2+y2+z2。(1)

图1

	Figure Option ViewDownloadNew Window
	图1 均匀半空间体元

在地表M(a, 0, 0)处可观测到电位值U, 在均匀半空间中与U_P之间是线性关系, 即

U=CUP=CIρ2πx2+y2+z2, (2)

式中C为比例系数。如果改变P点的电阻率, 假设变化量为Δ ρ , 那么在M点可以观测到相应的电位改变值Δ U, 其计算公式为^{[7, 8, 9]}

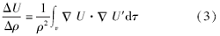
式中:dτ 为P点体元, U'假设为M点供电在A点观测到的电位。类似地, 其计算公式为

U'=CIρ2π(x-a)2+y2+z2。(4)

将式(2)、式(4)代入式(3), 可以得出结论, 式

(3)中的被积函数为二次复合函数, 定义

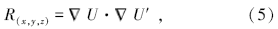
R_{(x, y, z)}反映了体元dτ 电阻率变化Δ ρ 时地表的电位响应程度, 这里称其为响应函数。显然, 对地面上特定的点(x, y, 0), 响应函数的值取决于体元的深度z及电极间距a, 而且据式(5), 该函数存在唯一极大值点, 也即存在适当z、a值, 对应的电位值变化最大, 此时的单位电极距a在理论上即是观测z深度地质体电位值的最佳极距。根据这一原理, 如果给定目标深度z, 就可以利用响应函数的最大值计算最佳电极距a, 反之, 对一拟定好的电极距, 可以根据最大响应值条件预估其可能的勘探深度。比较合理的方法是, 以响应函数极大值为中心, 计算一定区间内的z、a值, 然后以响应函数的平均值或中值所对应的z、a值作为最佳值, 以其作为极距选择或深度预估的依据。

这一结论在生产实际中具有重要意义, 特别是在直流电法测深的极距选择中, 利用这一结论, 可以根据解决问题的需要有针对性地选择电极序列, 有效提高勘探效果。笔者提出的等深模式电极序列法即是基于此原理。

图1中由A、M组成的电极系实际上就是一个两极装置, 上述公式反映的是两极装置的情况, 对其他装置的公式也可以类推得到。

以Wenner-Schlumberger对称四极装置测深为例进行说明。图2中, A、B为供电电极, M、N观测电极, AM=BN=na。只要确定了最佳a值, 即可计算各电极点位及序列长度^[10]。

图2

	Figure Option ViewDownloadNew Window
	图2 Wenner-Schlumberger测深装置

四极装置的响应函数要考虑MN之间的变化, 可以根据电场的叠加原理, 参照两极装置方法推导。

从响应函数的性质可以知道, 体元深度及电极距是影响响应函数形态的主要参数。由于本文讨论的内容主要是针对某一测点电极序列的选择问题, 因此为了获取响应函数的表达式, 可以将测点作为坐标原点。同时, 假设点电源强度为1 A, 即单位电流, 并定义一个比值:

Za=ZEna, (6)

式中, Z_E为目标勘探深度, n为单位电极距a的倍数(小数或整数均可), 也即定义AM、BN长度的系数。那么, M、N间响应函数仅是以Z_a为自变量的一元复合二次函数, 简写为 RMN=f(Za)。可见, 只要通过求取极值的方式确定响应函数极大值对应的Z_a值, 那么很容易根据目标深度Z_E确定最佳的电极距na; 反之, 根据已拟定电极距, 可以预估该电极系的理论勘探深度。

对一个电测深项目而言, 可以根据目标体的深度有选择性地设计电极序列方案。一般的做法是:以目标深度为主要研究对象, 充分预测目标体规模的大小, 按等深模式方式或大致均分布的原则确定电极序列, 使电极序列在深度上能有效覆盖目标体范围, 并确保在目标体范围内有足够的信息密度。这就是等深模式电极法的基本思想。

表1为一个按等深模式建立的电极序列实例, 该序列既考虑了施工的便利性, 也考虑了反演解释^{[11, 12, 13]}时电极序列的规律性。

表1

表1

表1 对称四极装置等深模式法电极序列 a/m n AB/m MN/m Δ ZE/m 2 1 6 2 6 2 30 6 4.5 10 2 50 10 3.71 10 3 70 10 4.03 10 5 110 10 7.80 20 4 180 20 13.21 40 4 360 40 34.01 40 5 440 40 15.22 60 4 540 60 18.71 60 5 660 60 23.32 100 4 900 100 44.12 120 4 1080 120 34.02 140 4 1260 140 34.11 160 4 1440 160 34.14 180 4 1620 180 34.16 200 4 1800 200 34.13

表1 对称四极装置等深模式法电极序列

由表1可知, 在AB=660~1 800 m段, 相邻电极序列间等深模式按等差规律设计, 公差约为34 m, 能使采集的深部数据既满足均匀分布又有较高信息密度, 可以有效提高对深部地质体的分辨能力; 而对小极距, 相邻等深模式公差保持在4~7 m之间, 能满足浅部小规模地质体的分辨要求。装置的最大长度为1 800 m, 最大理论勘探深度约341 m, 介于AB/5~AB/6之间, 与传统方法的评估结果基本一致, 但相对于传统方法而言, 响应函数给出了更明确的理论依据。

以上给出了等深模式电极序列法的定义, 对其他装置, 如三极、两极、偶极等, 均可按同样的原理计算合理的Z_a值, 以确定最佳的电极序列。

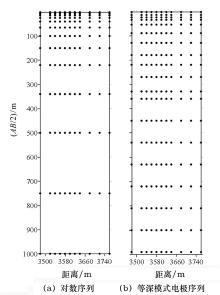
在地面大深度测深中使用较为频繁的仍然是按1963年的规范提出的电极序列, 即A、B供电电极的组合是:AB/2=1.5, 2.5, 4, 6, 9, 15, 25, 40, 65, 100, 150, 220, 340, 500, 750, 1000, 1500, 2000 m, …。该极距序列在对数坐标轴上基本为等间隔序列, 属于对数模式^[11]。以某金矿区的实测剖面为例, 对数模式与等深模式序列的断面点位分布见图3。

图3

	Figure Option ViewDownloadNew Window
	图3 某金矿区不同序列的点位分布对比

对数序列的点位集中在小极距区域, 而在大极距段, 相邻电极序列间对应的等效深度跨度过大, 显然无法获得处于此跨度内异常体的最强信息, 而等深模式序列法的点位既在小极距范围内保持了足够的点位密度, 也在大极距时保证了点位的均匀性; 相比之下, 等深模式法的深部数据具有更高的采集密度, 在畸变数据处理及解释结果的可靠性上也具有更明显的优势。等深模式法电极序列的规律性明显, 各电极均是按单位电极距的倍数推算, 这也为后期2D反演计算提供了便利。同时, 按等深模式原理, 可以根据目标体情况灵活选择电极距, 减少了电测深电极距选择的盲目性。

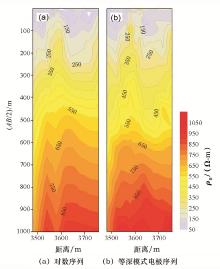
图4为某金矿区的实测物探剖面。该测区地形较为平坦, 地表为第四系砂质黏土覆盖, 隐伏地层为白云母绢云千枚状片岩, 物探剖面的主要任务是向外围追索深部构造。图4b为等深模式电极序列法的实测视电阻异常等值图, 以各电极距对应的理论深度为参考, 同比换算成对数序列法, 换算后的结果可以近似于按对数序列法采集的实测数据, 生成的等值线见图4a。对比显示, 图4b等值线更圆滑, 视电阻率的细节更加突出, 高阻体电阻率由浅至深的变化规律非常清楚, 高阻、低阻异常过渡较为平稳。图4a视电阻率等值线总体特征基本一致, 但在异常的细节展示上较差, 特别在中深部, 3 600点等值线存在明显向下强拉现象, 导致等值线形状过于尖锐, 场源畸变程度明显放大, 这显然受到了等效深度跨度太大导致数据点过稀的影响, 特别是对 3 600点旁AB/2为500~600 m间的高、低阻过渡区, 特征反映很不明显。

图4

	Figure Option ViewDownloadNew Window
	图4 某金矿区不同方式实测ρ s结果

采用响应函数极值分析结果确定最佳Z_a值后, 可以利用式(6)预估各电极距对应的理论勘探深度H。例如:AB=70 m, MN=10 m时对应的理论勘探深度H=12.24 m, 将每组电极换算成相应的H值后, 就可以绘制用理论勘探深度表示的视电阻率拟断面(图5a)。相对图4b, 图5a更直观地反映了视电阻率异常与深度的关系。图5b为采用最小二乘法对实测数据进行反演的结果, 视电阻率拟合均方误差6.3%。

图5

	Figure Option ViewDownloadNew Window
	图5 某金矿区的视电阻率拟断面(a)和反演电阻率断面(b)

不考虑异常细节的变化, 只考虑异常的形态和特征, 对比图5a、b可知, 在异常特征、电阻率值、等值线展布等各个方面, 两者在深度的对应上具有较高的一致性。这一结果为利用理论勘探深度展示视电阻率异常的合理性和精确性提供了生产依据, 在野外异常快速分析时具有较好的指导作用。经验表明, 在某一工作区, 当存在已知剖面时, 将已知条件及反演结果与理论勘探深度进行对比, 可获取经验参数, 并利用这一参数对理论勘探深度纠正, 可以大大提高快速分析的效果, 特别是浅部异常, 有时能直接得到高精度的推断结果。

1)均匀半空间体元电阻率变化导致地面观测电位的变化, 两者之间存在响应函数, 对特定的观测装置而言, 该函数是体元深度z与地表单位电极距a的函数, 为z与a的关系提供了新的研究方法; 该函数存在唯一极值点, 并且根据极值点可以估算体元深度z与单位电极长度a的比例系数Z_a。这一系数在生产实践中具有非常重要的理论意义:首先, 可以根据地质目标体的大概深度确定观测装置的总长度, 减少相关工作设计的盲目性; 其二, 可以有效设计针对目标体的电极序列, 确保在目标深度范围具有足够的信息密度, 增加测深装置的深部分辨力, 提高解释结果的准确性; 其三, 在野外快速分析工作中, 可以代替以往的量板法、经验法等手段, 从理论上更直观地得到异常体所在深度范围, 大大提高快速分析的准确性和效率。

2)基于响应函数提出的等深模式电极序列法提高了各类测深装置电极选择的灵活性和目的性, 在实际工作中, 只要确定了a的大小和装置类型, 通过简单的计算程序就可以针对目标深度提出多种电极序列方案, 并同时给出所有序列电极布点点位, 提高野外跑极效率。

3)文中以对称四极测深为例阐述了从等深模式电极序列原理到实际生产的完整过程, 其他类型的装置也可以按照类似的方法推导公式, 选择最佳电极序列。